Download to read offline
More Related Content
Carnot Cycle
- 1. Presentation on CarnotCycle Presented by: Ranjit Dey Student Code: BWU/BTD/22/165 Course Code: BSCD101 Course Name: Engineering Chemistry
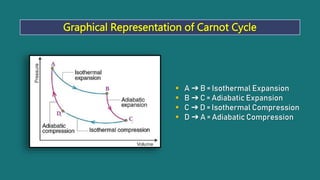
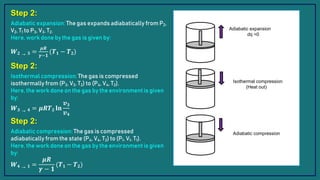
- 2. The Carnotcycle is hypothetical cycle consists of four processes as two reversible isothermal process and two reversible adiabatic process. The Cycle was proposed in 1824 by French engineer, Sadi Carnot. Carnot Cycle
- 3. All typesof vehicles that we use like cars, motorcycles, trucks, ships, aero planes etc. work on the basis of second law of thermodynamics and Carnot Cycle. They may be using petrol engine or diesel engine, but the law remains same Application
- 4. Application All therefrigerators, deep freezers, industrial refrigeration systems, all types of air-conditioning systems, heat pumps, etc work on the basis of the Carnot Cycle.
- 5. Graphical Representation ofCarnot Cycle A ➔ B = Isothermal Expansion B ➔ C = Adiabatic Expansion C ➔ D = Isothermal Compression D ➔ A = Adiabatic Compression
- 6. Process of CarnotCycle
- 7. Carnot Theorem All reversibleheat engines operating between the same two heat reservoirs must have the same efficiency. Noheat engine operating between two heat reservoirs can be more efficient than a reversible heat engine operating between the same two reservoirs.
- 8. Steps involved ina Carnot Cycle For an ideal gas operating inside a Carnot cycle, the following steps are involved Step 1: Isothermal expansion: The gas is taken from P1, V1, T1 to P2, V2, T2. Heat Q1 is absorbed from the reservoir at temperature T1. Since the expansion is isothermal, the total change in internal energy is zero, and the heat absorbed by the gas is equal to the work done by the gas on the environment, which is given as: delT =0 V = +ve Isothermal Expansion 𝑊1 → 2 = 𝑄1 = 𝜇 × 𝑅1 × 𝑇1 × ln 𝑣2 𝑣1
- 9. Adiabatic expansion dq =0 Isothermalcompression (Heat out) Adiabatic compression Step 2: Adiabatic expansion: The gas expands adiabatically from P2, V2, T1 to P3, V3, T2. Here, work done by the gas is given by: 𝑾𝟐 → 𝟑 = 𝝁𝑹 𝜸−𝟏 (𝑻𝟏 − 𝑻𝟐) Step 2: Isothermal compression: The gas is compressed isothermally from (P3, V3, T2) to (P4, V4, T2). Here, the work done on the gas by the environment is given by: 𝑾𝟑 → 𝟒 = 𝝁𝑹𝑻𝟐 𝐥𝐧 𝒗𝟑 𝒗𝟒 Step 2: Adiabatic compression: The gas is compressed adiabatically from the state (P4, V4, T2) to (P1, V1, T1). Here, the work done on the gas by the environment is given by: 𝑾𝟒 → 𝟏 = 𝝁𝑹 𝜸 − 𝟏 (𝑻𝟏 − 𝑻𝟐)
- 10. Hence, the totalwork done by the gas on the environment in one complete cycle is given by: 𝑊 = W1 → 2 + W2 → 3 + W3 → 4 + W4 → 1 𝑊 = 𝜇𝑅𝑇1 ln 𝑣2 𝑣1 − 𝜇𝑅𝑇2 ln 𝑣3 𝑣4 𝐸𝑓𝑓𝑖𝑐𝑖𝑒𝑛𝑐𝑦 = 𝑊 𝑄1 = 𝑄1 − 𝑄2 𝑄1 = 1 − 𝑄2 𝑄1 = 1 − 𝑇2 𝑇1 ln 𝑣3 𝑣4 ln 𝑣2 𝑣1 Since the step 2 →3 is an adiabatic process, we can write 𝑇1𝑉2 − = 𝑇2𝑉3 − Or, 𝑣2 𝑣3 = ( 𝑇2 𝑇1 ) 1 𝛾−1 Similarly, for the process 4 → 1, we can write 𝑣2 𝑣3 = ( 𝑇2 𝑇1 ) 1 𝛾−1 ⇒ 𝑣2 𝑣3 = 𝑣1 𝑣2 So, the expression for net efficiency of Carnot engine reduce to: 𝑁𝑒𝑡 𝑒𝑓𝑓𝑖𝑐𝑖𝑒𝑛𝑐𝑦 = 1 − 𝑇2 𝑇1 𝑁𝑒𝑡 𝑒𝑓𝑓𝑖𝑐𝑖𝑒𝑛𝑐𝑦 = 𝑁𝑒𝑡 𝑤𝑜𝑟𝑘𝑑𝑜𝑛𝑒 𝑏𝑦 𝑡ℎ𝑒 𝑔𝑎𝑠 𝐻𝑒𝑎𝑡 𝑎𝑏𝑠𝑜𝑟𝑏𝑒𝑑 𝑏𝑦 𝑡ℎ𝑒 𝑔𝑎𝑠
- 11. Limitations of CarnotCycle The limitations of Carnot Cycle are as follows: • The Carnot Cycle is an ideal cycle which means that did not exist and impossible to construct so, it is just a theoretical concept. • The isothermal process says that the temperature is constant but the Carnot Cycle explains there will be heat addition in the isothermal expansion process which is not possible. • The Carnot Cycle is used to study the heat engine and not extend to other types of devices.