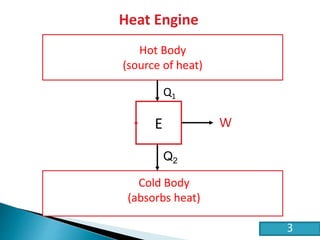
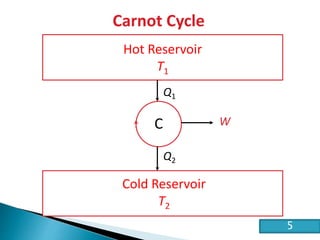
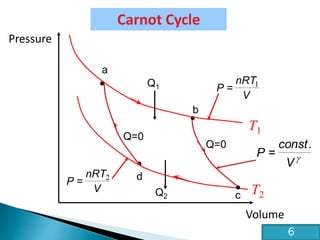
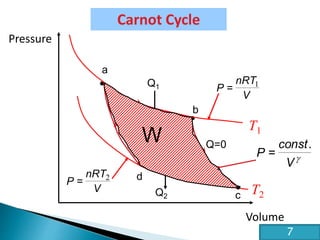
This document discusses the Carnot cycle and the second law of thermodynamics. It defines a heat engine and describes the key components of the Carnot cycle, including the isothermal and adiabatic processes. It explains that the Carnot cycle is reversible and defines the maximum possible efficiency for converting heat into work. The document concludes by stating the Kelvin-Planck and Clausius formulations of the second law - that it is impossible to convert all heat from a single body into work or to spontaneously transfer heat from a cold to hot body.

1. Department of Physics
Topic –Carnot Cycle
Prof. B.V. Tupte
Head, Department of Physics
Shri Govindrao Munghate Arts and Science
College Kurkheda.

2. HE2 Thermal Physics

3. HE2 Thermal Physics
Heat Engine
• A heat engine is a device that absorbs heat (Q) and uses it
to do useful work (W) on the surroundings when operating
in a cycle.
• Sources of heat include the combustion of coal, petroleum
or carbohydrates and nuclear reactions.
• Working substance: the matter inside the heat engine
that undergoes addition or rejection of heat and that does
work on the surroundings. Examples include air and water
vapour (steam).
• In a cycle, the working substance is in the same
thermodynamic state at the end as at the start.
1

4. HE2 Thermal Physics
2

5. HE2 Thermal Physics
Heat Engine
E
Hot Body
(source of heat)
Q1
Cold Body
(absorbs heat)
Q2
W
3

6. HE2 Thermal Physics
Efficiency of a Heat Engine
Efficiency, h = Work out/Heat in:
Apply First Law to the working substance:
DU = Q1 – Q2 – W
But in a cycle, DU = 0
Thus, W = Q1 – Q2.
1
2
1
2
1
1
1
Q
Q
Q
Q
Q
Q
W





h
Substituting:
1
Q
W

h
Lesson: h is maximum when Q2 is minimum.
4

7. HE2 Thermal Physics
Carnot Cycle
Hot Reservoir
T1
Cold Reservoir
T2
C
Q1
Q2
W
5

8. HE2 Thermal Physics
Volume
Pressure
•
•
a
b
•
d
T1
Q1
Carnot Cycle
Q2
V
nRT
P 1
=

V
const
P
.
=
T2
•
c
Q=0
Q=0
V
nRT
P 2
=
6

9. HE2 Thermal Physics
Volume
Pressure
•
•
a
b
•
d
T1
Q1
Q2
V
nRT
P 1
=

V
const
P
.
=
T2
•
c
Q=0
Q=0
V
nRT
P 2
=
W
Carnot Cycle
7

10. HE2 Thermal Physics
From a to b: isothermal, so that DU = 0 and Q = - W
Thus, Q1 = +nRT1ln(Vb/Va) (+ve quantity)
Carnot Cycle
Similarly, from c to d: isothermal, so that DU = 0 and Q = - W
Thus, Q2 = +nRT2ln(Vd/Vc) = -nRT2ln(Vc/Vd) (-ve)
From b to c: adiabatic, Q = 0, so that TV-1 is constant.
Thus, T1Vb
-1 = T2Vc
-1 or 1
2
1











b
c
V
V
T
T
Similarly, d to a: adiabatic, Q = 0, so that TV-1 is constant.
Thus, T2Vd
-1 = T1Va
-1 or 1
2
1











a
d
V
V
T
T
8

11. HE2 Thermal Physics
Carnot Cycle
We see that:
1
1
2
1






















a
d
b
c
V
V
V
V
T
T
)
/
ln(
)
/
ln(
)
/
ln(
)
/
ln(
2
1
2
1
2
1
d
c
a
b
d
c
a
b
V
V
T
V
V
T
V
V
nRT
V
V
nRT
Q
Q


a
b
d
c
V
V
V
V

Which means that
Now also:
This is an important result. Temperature can be defined (on the
absolute (Kelvin) scale) in terms of the heat flows in a Carnot
Cycle.
But as the volume
ratios are equal: 2
1
2
1
T
T
Q
Q

9

12. HE2 Thermal Physics
What’s Special about a Carnot Cycle?
(1) Heat is transferred to/from only two reservoirs at fixed
temperatures, T1 and T2 - not at a variety of temperatures.
(2) Heat transfer is the most efficient possible because the
temperature of the working substance equals the temperature
of the reservoirs. No heat is wasted in flowing from hot to cold.
(3) The cycle uses an adiabatic process to raise and lower the
temperature of the working substance. No heat is wasted in
heating up the working substance.
(4) Carnot cycles are reversible. Not all cycles are!
10

13. HE2 Thermal Physics
What’s Special about a Carnot Cycle?
(5) The Carnot theorem states that the Carnot cycle (or any
reversible cycle) is the most efficient cycle possible. The Carnot
cycle defines an upper limit to the efficiency of a cycle.
• Where T1 and T2 are the temperatures of the hot and cold
reservoirs, respectively, in degrees Kelvin.
 As T2 > 0, hc is always <1.
• Recall that for any cycle, the efficiency of a heat engine is
given as:
1
2
1
1
=
=
Q
Q
Q
W
E
h
• For an engine using a Carnot cycle, the efficiency is also
equal to:
1
2
1
=
T
T
C
h
11

14. HE2 Thermal Physics
Kelvin-Planck Statement of the Second Law of
Thermodynamics
“It is impossible to construct a device that - operating in a
cycle - will produce no other effect than the extraction of
heat from a single body and the performance of an
equivalent amount of work”
Or…A cyclical engine cannot convert heat from a single
body completely into work. Some heat must be rejected
at a lower temperature. Thus, efficiency, h < 1!
12

15. HE2 Thermal Physics
Clausius Statement of the Second Law of
Thermodynamics
(applies to refrigerators)
“It is impossible to construct a device that - operating in a
cycle - will produce no other effect than heat transfer from
a colder body to hotter body.”
“Or…Heat cannot flow from a cold body to a hotter body
by itself. Work has to be done in the process.”
13