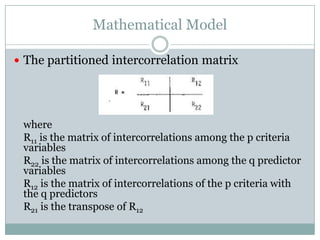
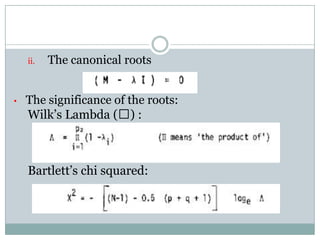
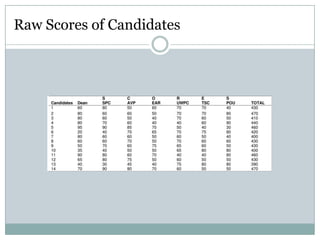
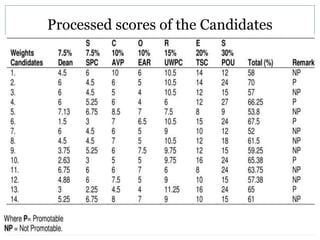
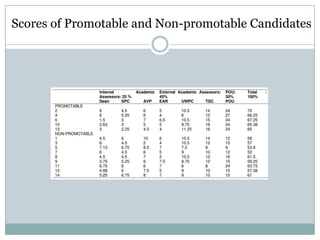
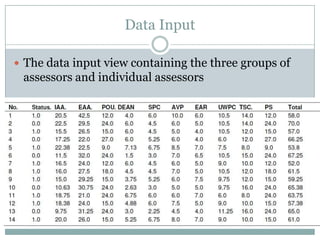
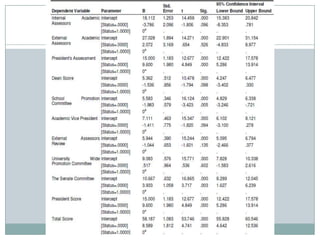
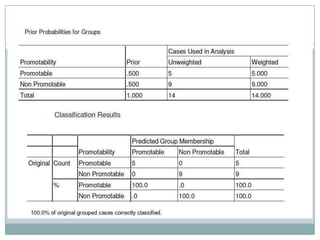
Canonical correlation analysis was used to detect potential bias in faculty promotion scoring at the American University of Nigeria (AUN). The analysis compared scores from three promotion committees and tested whether any committee showed bias that influenced candidates' promotability. The analysis found: 1) It could discriminate between candidates deemed promotable versus non-promotable, rejecting the hypothesis that it couldn't do so. 2) There were no significant differences in scoring between committees, rejecting the hypothesis that it couldn't detect bias. 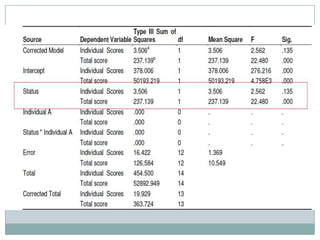3) Only the president's committee showed significant score weight influence on promotability, rejecting the hypothesis that it couldn't detect overbearing influences. The study demonstrated canonical correlation analysis can be an effective tool for unbiased faculty

1. Canonical Correlation

2. Introduction If we have two sets of variables, x1,...., xn and y1,….., ym, and there are correlations among the variables, then canonical correlation analysis will enable us to find linear combinations of the x's and the y's which have maximum correlation with each other. Canonical correlation begin with the observed values of two sets of variables relating to the same set of areas, and a theory or hypothesis that suggests that the two are interrelated. The overriding concern is with the structural relationship between the two sets of data as a whole, rather than the associations between individual variables

3. Canonical correlation is the most general form of correlation. Multiple regression analysis is a more specific case in which one of the sets of data contains only one variable, while product moment correlation is the most specific case in that both sets of data contain only one variable. Canonical correlation analysis is not related to factor/principal components analysis despite certain conceptual and terminological similarities. Canonical correlation analysis is used to investigate the inter-correlation between two sets of variables, whereas factor/principal components analysis identifies the patterns of relationship within one set of data.

4. Difficulties in Canonical Correlation Canonical correlation is not the easiest of techniques to follow, though the problems of comprehension are conceptual rather than mathematical. Unlike multiple regression and principal components analysis, we cannot provide a graphic device to illustrate even the simplest form. For with canonical correlation analysis we are dealing with two sets of data. Even the most elementary example must, therefore, have at least two variables on each side and so we require 2 + 2 = 4 dimensions. Tied as we are, however, to a three dimensional world, a true understanding of the technique in the conventional cognitive/visual sense of the term, is beyond our grasp.

5. Conceptual Overview Data Input The size of the matrices : There is no requirement in canonical analysis that there must be the same number of variables (columns) in each matrix, though there must be the same number of areas (rows). (There must of course be more than one variable in each set otherwise we would be dealing with multiple regression analysis) The order of the matrices : Neither set of data is given priority in the analysis so it does not matter which we term the criteria and which the predictors. Unlike simple linear regression there is no concept of a 'dependent' set or an 'independent' set. But in practice the smaller set is always taken second as this simplifies the calculation enormously

6. Advantages Useful and powerful technique for exploring the relationships among multiple dependent and independent variables. Results obtained from a canonical analysis should suggest answers to questions concerning the number of ways in which the two sets of multiple variables are related, the strengths of the relationships. Multiple regressions are used for many-to-one relationships, canonical correlation is used for many-to-many relationships. Canonical Correlation- More than one such linear correlation relating the two sets of variables, with each such correlation representing a different dimension by which the independent set of variables is related to the dependent set.

8. The Canonical Problem Latent Roots and weights Canonical Scores Results and Interpretation Latent Roots Canonical Weights Canonical Scores

9. Mathematical Model The partitioned intercorrelation matrix where R11 is the matrix of intercorrelations among the p criteria variables R22 is the matrix of intercorrelations among the q predictor variables R12 is the matrix of intercorrelations of the p criteria with the q predictors R21 is the transpose of R12

10. The Canonical Equation The product matrix

14. Canonical correlation analysis-promotion bias scoring detector(a case study of American university of Nigeria(AUN)) Researchers-A. O. Unegbu & James J. Adefila `

15. Introduction Problem: AUN bids to keep with her value statement i.e. highest standards of integrity, transparency and academic honest. Solution: Appraise & select Faculties for promotion based on various promotion committees’ scores. Issues : Dwindling funding, need for a bias free selection technique,

17. H02: CCA cannot detect significantly whether or not score-weights of each of the Promotion Assessors have over bearing influence on the promotability of candidates.

19. Steps of the Research Data collection Manual computations SPSS analysis Test the Hypothesis

20. AUN promotion procedure Weights: The benchmark for promotion is securing a weighted average score should be more than 65%age.

21. Each of the Committee’s point allocation will be based on the below criteria

22. Supporting documents for Teaching Effectiveness Peer evaluation Student evaluation Course Syllabi Record of participation in teaching seminars, workshops, etc Contributions to the development of new academic programs Faculty awards for excellence in teaching

23. Scholarship, Research and Creative Works Terminal degrees/Professional qualifications At least Five publications, three of which shall be journal articles Computer Software and Program development Creative work in the areas of advertising, public relations, layout design, photography and graphics, visual arts etc.

24. Service to the University, Profession and Community Membership/leadership in departmental, school-wide or university-wide committees Planning or participation in workshops, conferences, seminars . Evidence of participation in mentoring or career counseling of students. Membership in Civil Society organizations Evidence of service as external assessor or external examiner on examination committees

25. Raw Scores of Candidates

26. Processed scores of the Candidates

27. Scores of Promotable and Non-promotable Candidates

28. Data Input The data input view containing the three groups of assessors and individual assessors

29. SPSS Results Analyze ⇒General Linear Model⇒Multivariate SPSS classified candidates into two groups of promotable and non promotable of 5 and 9 respectively. The result leads to the rejection of Null hypothesis Ho3 which states that Canonical Correlation Analysis cannot with 90% confidence level discriminate between promotable and non promotable candidates

32. Candidate’s status determination resulting from scores across the assessors and those that might result from bias scoring are very insignificant(Wilk’s lambda value =0.041)

33. There is no between-status differences in the scores between assessors of both group and individuals

35. The results of the table show that the scores of each assessor had a significant effect on the determination of each Candidate Status as the significance is 0.135.

36. Test for homogeneity of variance Overbearing score weight influence test hypothesis is aimed at detecting across the individual assessors’ mark allocations and weights assigned to each. In this test, the assessors having low significance value mean that there is homogeneity of variance.

38. This Leads to rejection of null hypothesis (Ho2) which states that Canonical Correlation Analysis cannot detect significantly whether or not score-weights of each of the promotion assessors has overbearing influence on the promotability of candidates.

41. Continued…………. Rejection of Null Hypothesis(Ho1):Pillar’s trace of 0.041, Wilk’s Lambda of 0.041, Hotelling’s trace of 0.041 and Roy’s Largest Root of 0.041 - all of them showed that p<0.05, it means that there is no between-status differences in the scores between assessors of both group and individuals, thereby leading to the rejection of Null hypothesis (Ho1) which states that Canonical Correlation Analysis cannot detect bias. Rejection of Null Hypothesis(Ho2):For Group Assessors - Internal Assessors with p=0.096, External Academic Assessors with p=0.526 and The President’s Assessment with p=0.0001, shows that except that of the President, the weight assigned to scores of other two are group assessors are insignificant- lead us to reject the Null hypothesis (Ho2) which states that Canonical Correlation Analysis cannot detect significantly whether or not score-weights of each of the promotion assessors has overbearing influence on the promotability of candidates.

42. Thank You !!