Uploaded byStanfordComputationalImaging
PPTX, PDF805 views

Build Your Own VR Display Course - SIGGRAPH 2017: Part 2

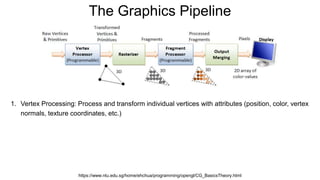
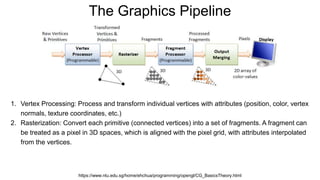
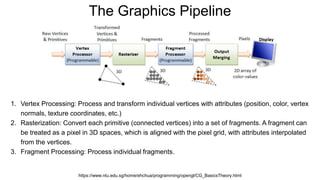
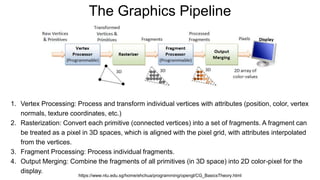
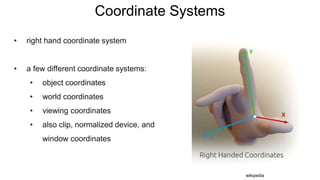
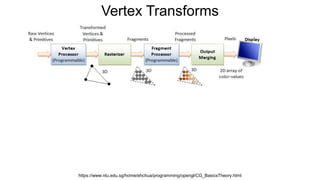
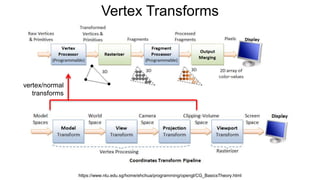
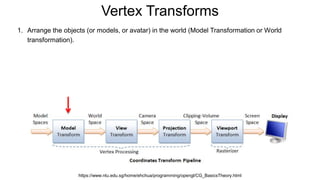
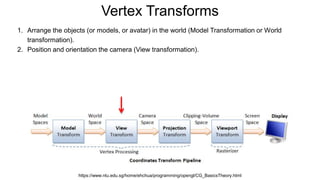
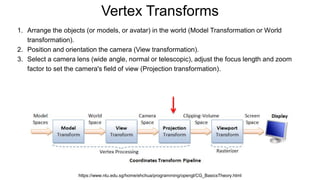
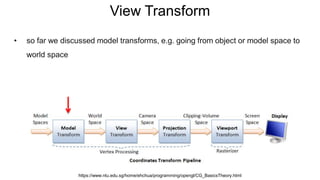
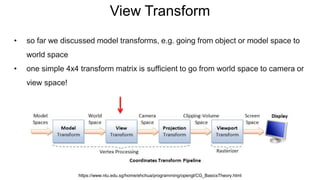
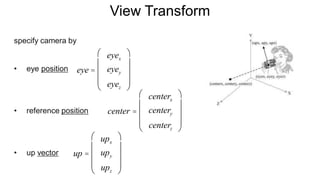
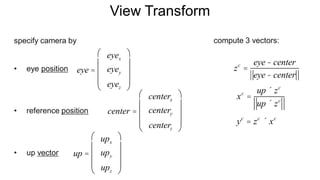
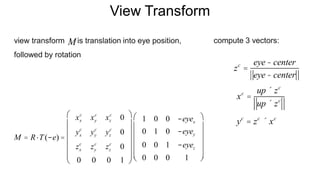
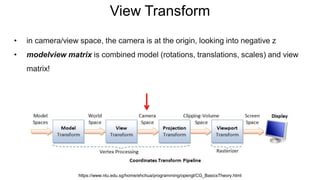
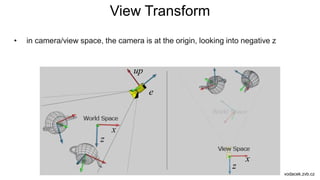
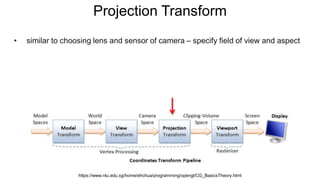
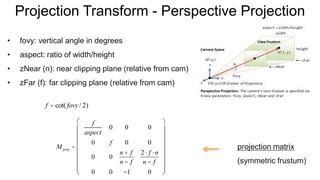
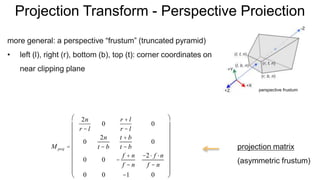
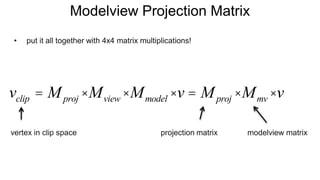
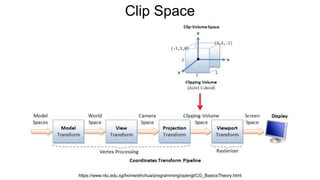
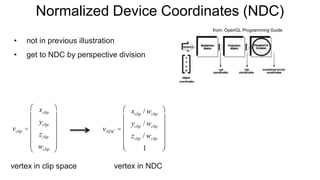
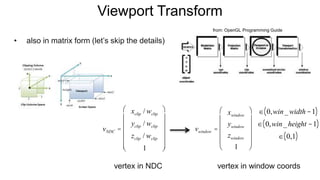
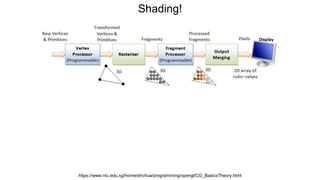
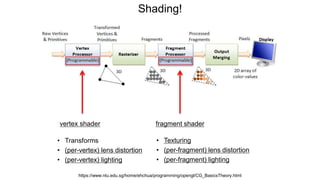
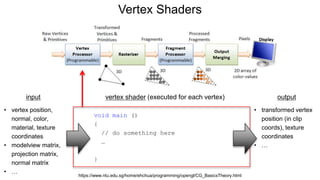
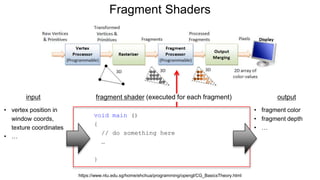
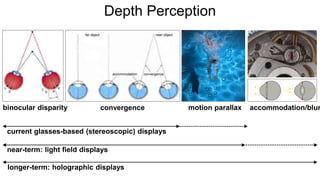
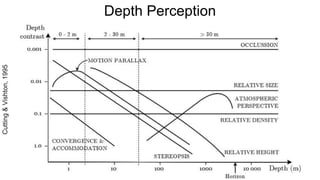
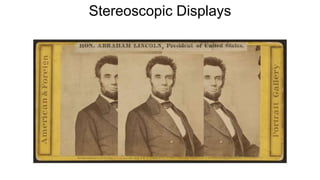
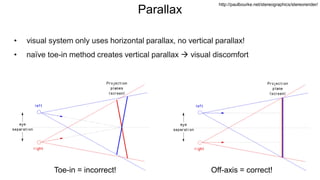
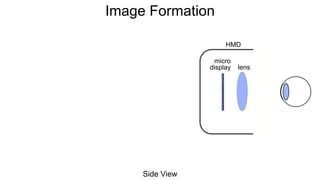
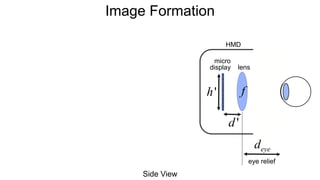
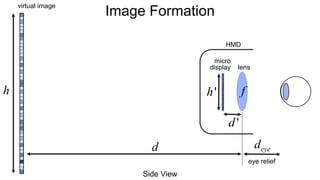
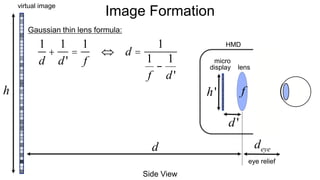
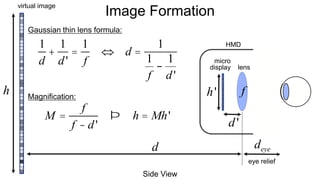
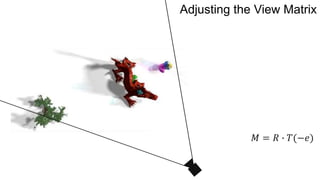
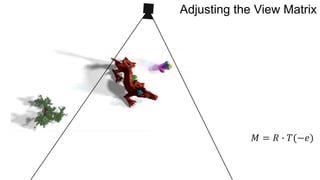
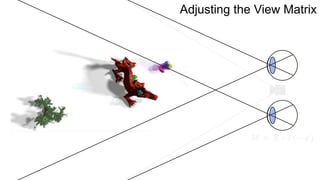
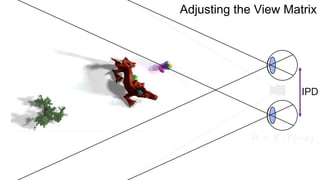
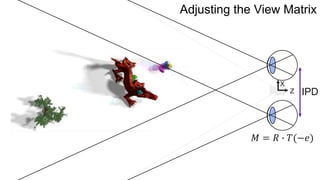
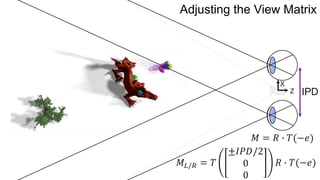
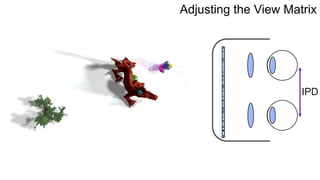
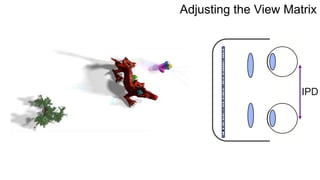
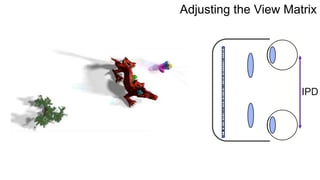
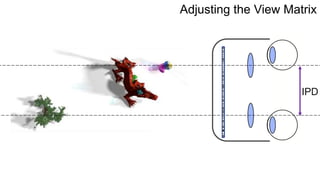
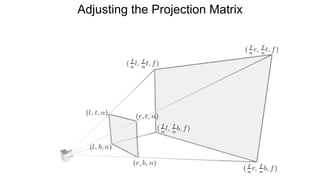
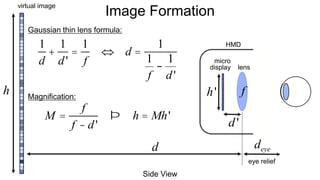
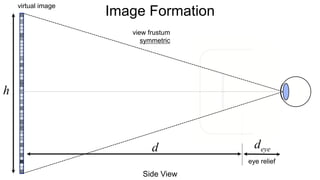
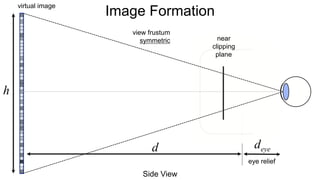
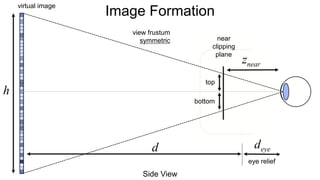
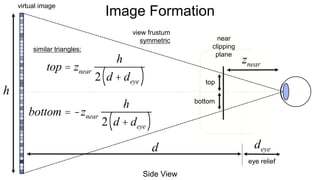
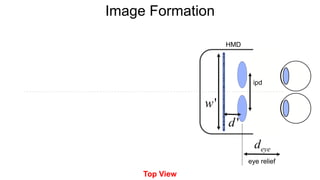
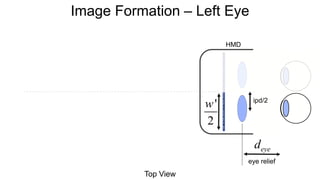
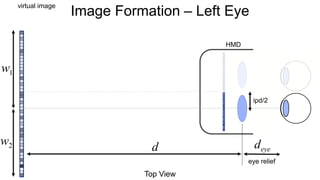
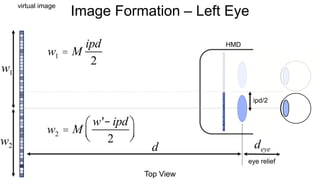
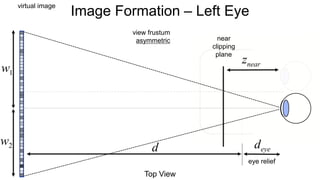
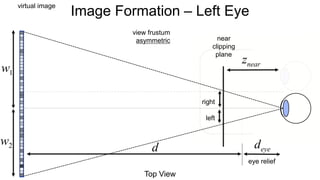
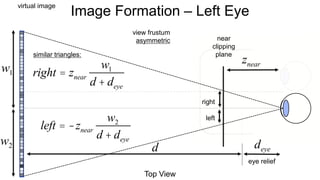
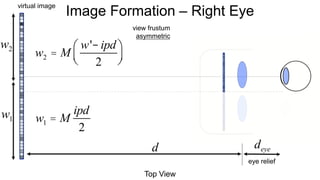
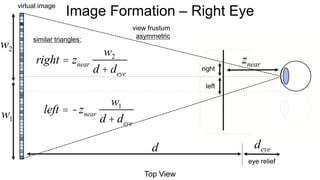
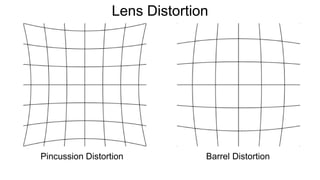
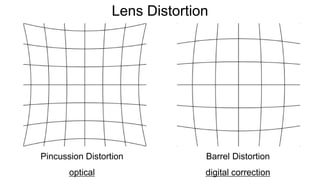
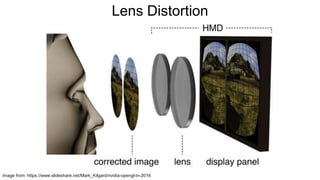
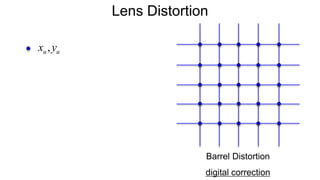
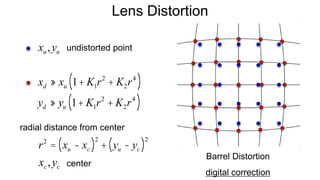
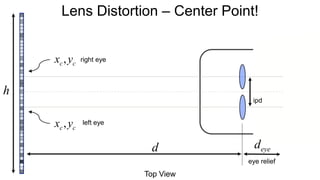
The document discusses the graphics rendering pipeline for virtual reality displays. It covers topics such as the graphics pipeline, stereo rendering, coordinate space transformations, shaders, lens distortion, and using WebGL and three.js for 3D graphics rendering in web browsers. The graphics pipeline involves vertex processing, rasterization, and fragment processing to convert 3D scene descriptions into 2D images. Key steps include model, view, and projection transformations as well as vertex and fragment shaders. Stereo rendering and lens distortion are also covered to enable VR displays.

Engineering◦
Related topics:
Virtual Reality•

Embed presentation

Downloaded 52 times
1 / 123
2 / 123
3 / 123
4 / 123
5 / 123
6 / 123
7 / 123
8 / 123
9 / 123
10 / 123
11 / 123
12 / 123
13 / 123
14 / 123
15 / 123
16 / 123
17 / 123
18 / 123
19 / 123
20 / 123
21 / 123
22 / 123
23 / 123
24 / 123
25 / 123
26 / 123
27 / 123
28 / 123
29 / 123
30 / 123
31 / 123
32 / 123
33 / 123
34 / 123
35 / 123
36 / 123
37 / 123
38 / 123
39 / 123
40 / 123
41 / 123
42 / 123
43 / 123
44 / 123
45 / 123
46 / 123
47 / 123
48 / 123
49 / 123
50 / 123
51 / 123
52 / 123
53 / 123
54 / 123
55 / 123
56 / 123
57 / 123
58 / 123
59 / 123
60 / 123
61 / 123
62 / 123
63 / 123
64 / 123
65 / 123
66 / 123
67 / 123
68 / 123
69 / 123
70 / 123
71 / 123
72 / 123
73 / 123
74 / 123
75 / 123
76 / 123
77 / 123
78 / 123
79 / 123
80 / 123
81 / 123
82 / 123
83 / 123
84 / 123
85 / 123
86 / 123
87 / 123
88 / 123
89 / 123
90 / 123
91 / 123
92 / 123
93 / 123
94 / 123
95 / 123
96 / 123
97 / 123
98 / 123
99 / 123
100 / 123
101 / 123
102 / 123
103 / 123
104 / 123
105 / 123
106 / 123
107 / 123
108 / 123
109 / 123
110 / 123
111 / 123
112 / 123
113 / 123
114 / 123
115 / 123
116 / 123
117 / 123
118 / 123
119 / 123
120 / 123
121 / 123
122 / 123
123 / 123
Build Your Own VR Display The Graphics Pipeline, Stereo Rendering, and Lens Distortion Robert Konrad Stanford University stanford.edu/class/ee267/
Image courtesy of Robo Recall
Albrecht Dürer, “Underweysung der Messung mit dem Zirckel und Richtscheyt”, 1525
Section Overview • The graphics rendering pipeline • Coordinate space transformations • Shaders • Stereo rendering • View matrix • Projection matrix • Lens distortion • Fragment shader • Vertex shader
WebGL • JavaScript application programmer interface (API) for 2D and 3D graphics • OpenGL ES 2.0 running in the browser, implemented by all modern browsers
WebGL • JavaScript application programmer interface (API) for 2D and 3D graphics • OpenGL ES 2.0 running in the browser, implemented by all modern browsers
WebGL • JavaScript application programmer interface (API) for 2D and 3D graphics • OpenGL ES 2.0 running in the browser, implemented by all modern browsers
WebGL • JavaScript application programmer interface (API) for 2D and 3D graphics • OpenGL ES 2.0 running in the browser, implemented by all modern browsers
WebGL • JavaScript application programmer interface (API) for 2D and 3D graphics • OpenGL ES 2.0 running in the browser, implemented by all modern browsers
WebGL • JavaScript application programmer interface (API) for 2D and 3D graphics • OpenGL ES 2.0 running in the browser, implemented by all modern browsers
three.js • cross-browser JavaScript library/API • higher-level library that provides a lot of useful helper functions, tools, and abstractions around WebGL – easy and convenient to use • https://threejs.org/ • simple examples: https://threejs.org/examples/ • great introduction (in WebGL): http://davidscottlyons.com/threejs/presentations/frontporch14/
Computer Graphics! • at the most basic level: conversion from 3D scene description to 2D image • what do you need to describe a static scene? • 3D geometry and transformations • lights • material properties / textures • Represent object surfaces as a set of primitive shapes • Points / Lines / Triangles / Quad (rilateral) s
Tesselation
The Graphics Pipeline https://www.ntu.edu.sg/home/ehchua/programming/opengl/CG_BasicsTheory.html 1. Vertex Processing: Process and transform individual vertices with attributes (position, color, vertex normals, texture coordinates, etc.)
The Graphics Pipeline https://www.ntu.edu.sg/home/ehchua/programming/opengl/CG_BasicsTheory.html 1. Vertex Processing: Process and transform individual vertices with attributes (position, color, vertex normals, texture coordinates, etc.) 2. Rasterization: Convert each primitive (connected vertices) into a set of fragments. A fragment can be treated as a pixel in 3D spaces, which is aligned with the pixel grid, with attributes interpolated from the vertices.
The Graphics Pipeline https://www.ntu.edu.sg/home/ehchua/programming/opengl/CG_BasicsTheory.html 1. Vertex Processing: Process and transform individual vertices with attributes (position, color, vertex normals, texture coordinates, etc.) 2. Rasterization: Convert each primitive (connected vertices) into a set of fragments. A fragment can be treated as a pixel in 3D spaces, which is aligned with the pixel grid, with attributes interpolated from the vertices. 3. Fragment Processing: Process individual fragments.
The Graphics Pipeline https://www.ntu.edu.sg/home/ehchua/programming/opengl/CG_BasicsTheory.html 1. Vertex Processing: Process and transform individual vertices with attributes (position, color, vertex normals, texture coordinates, etc.) 2. Rasterization: Convert each primitive (connected vertices) into a set of fragments. A fragment can be treated as a pixel in 3D spaces, which is aligned with the pixel grid, with attributes interpolated from the vertices. 3. Fragment Processing: Process individual fragments. 4. Output Merging: Combine the fragments of all primitives (in 3D space) into 2D color-pixel for the display.
Coordinate Systems • right hand coordinate system • a few different coordinate systems: • object coordinates • world coordinates • viewing coordinates • also clip, normalized device, and window coordinates wikipedia
Vertex Transforms https://www.ntu.edu.sg/home/ehchua/programming/opengl/CG_BasicsTheory.html
Vertex Transforms https://www.ntu.edu.sg/home/ehchua/programming/opengl/CG_BasicsTheory.html vertex/normal transforms
Vertex Transforms https://www.ntu.edu.sg/home/ehchua/programming/opengl/CG_BasicsTheory.html 1. Arrange the objects (or models, or avatar) in the world (Model Transformation or World transformation).
Vertex Transforms https://www.ntu.edu.sg/home/ehchua/programming/opengl/CG_BasicsTheory.html 1. Arrange the objects (or models, or avatar) in the world (Model Transformation or World transformation). 2. Position and orientation the camera (View transformation).
Vertex Transforms https://www.ntu.edu.sg/home/ehchua/programming/opengl/CG_BasicsTheory.html 1. Arrange the objects (or models, or avatar) in the world (Model Transformation or World transformation). 2. Position and orientation the camera (View transformation). 3. Select a camera lens (wide angle, normal or telescopic), adjust the focus length and zoom factor to set the camera's field of view (Projection transformation).
Vertex Transforms https://www.ntu.edu.sg/home/ehchua/programming/opengl/CG_BasicsTheory.html 1. Arrange the objects (or models, or avatar) in the world (Model Transformation or World transformation). 2. Position and orientation the camera (View transformation). 3. Select a camera lens (wide angle, normal or telescopic), adjust the focus length and zoom factor to set the camera's field of view (Projection transformation). 4. Print the photo on a selected area of the paper (Viewport transformation) - in rasterization stage
Model Transform • transform each vertex from object coordinates to world coordinates https://www.ntu.edu.sg/home/ehchua/programming/opengl/CG_BasicsTheory.html v = x y z æ è ç ç ç ö ø ÷ ÷ ÷
Summary of Homogeneous Matrix Transforms • translation • scale • rotation Rx = 1 0 0 0 0 cosq -sinq 0 0 sinq cosq 0 0 0 0 1 æ è ç ç ç ç ö ø ÷ ÷ ÷ ÷ Ry = cosq 0 sinq 0 0 1 0 0 -sinq 0 cosq 0 0 0 0 1 æ è ç ç ç ç ö ø ÷ ÷ ÷ ÷ Read more: https://www.ntu.edu.sg/home/ehchua/programming/opengl/CG_BasicsTheory.html T(d) = 1 0 0 dx 0 1 0 dy 0 0 1 dz 0 0 0 1 æ è ç ç ç ç ç ö ø ÷ ÷ ÷ ÷ ÷ S(s) = sx 0 0 0 0 sy 0 0 0 0 sz 0 0 0 0 1 æ è ç ç ç ç ç ö ø ÷ ÷ ÷ ÷ ÷ Rz (q) = cosq -sinq 0 0 sinq cosq 0 0 0 0 1 0 0 0 0 1 æ è ç ç ç ç ö ø ÷ ÷ ÷ ÷
Summary of Homogeneous Matrix Transforms • translation inverse translation • scale inverse scale • rotation inverse rotation T(d) = 1 0 0 dx 0 1 0 dy 0 0 1 dz 0 0 0 1 æ è ç ç ç ç ç ö ø ÷ ÷ ÷ ÷ ÷ S(s) = sx 0 0 0 0 sy 0 0 0 0 sz 0 0 0 0 1 æ è ç ç ç ç ç ö ø ÷ ÷ ÷ ÷ ÷ Rz (q) = cosq -sinq 0 0 sinq cosq 0 0 0 0 1 0 0 0 0 1 æ è ç ç ç ç ö ø ÷ ÷ ÷ ÷ Read more: https://www.ntu.edu.sg/home/ehchua/programming/opengl/CG_BasicsTheory.html T -1 (d) = T(-d) = 1 0 0 -dx 0 1 0 -dy 0 0 1 -dz 0 0 0 1 æ è ç ç ç ç ç ö ø ÷ ÷ ÷ ÷ ÷ S-1 (s) = S 1 s æ èç ö ø÷ = 1/ sx 0 0 0 0 1/ sy 0 0 0 0 1/ sz 0 0 0 0 1 æ è ç ç ç ç ç ö ø ÷ ÷ ÷ ÷ ÷ Rz -1 (q) = Rz -q( ) = cos-q -sin-q 0 0 sin-q cos-q 0 0 0 0 1 0 0 0 0 1 æ è ç ç ç ç ö ø ÷ ÷ ÷ ÷
Summary of Homogeneous Matrix Transforms • successive transforms: • inverse successive transforms: v' = T ×S×Rz ×Rx ×T ×v Read more: https://www.ntu.edu.sg/home/ehchua/programming/opengl/CG_BasicsTheory.html v = T ×S× Rz × Rx ×T( ) -1 ×v' = T -1 × Rx -1 × Rz -1 ×S-1 ×T -1 ×v'
Attention! • rotations and translations (or transforms in general) are not commutative! • make sure you get the correct order!
View Transform • so far we discussed model transforms, e.g. going from object or model space to world space https://www.ntu.edu.sg/home/ehchua/programming/opengl/CG_BasicsTheory.html
View Transform • so far we discussed model transforms, e.g. going from object or model space to world space • one simple 4x4 transform matrix is sufficient to go from world space to camera or view space! https://www.ntu.edu.sg/home/ehchua/programming/opengl/CG_BasicsTheory.html
View Transform specify camera by • eye position • reference position • up vector eye = eyex eyey eyez æ è ç ç ç ö ø ÷ ÷ ÷ up = upx upy upz æ è ç ç ç ö ø ÷ ÷ ÷ center = centerx centery centerz æ è ç ç ç ö ø ÷ ÷ ÷
View Transform specify camera by • eye position • reference position • up vector up = upx upy upz æ è ç ç ç ö ø ÷ ÷ ÷ center = centerx centery centerz æ è ç ç ç ö ø ÷ ÷ ÷ compute 3 vectors: eye = eyex eyey eyez æ è ç ç ç ö ø ÷ ÷ ÷ xc = up ´ zc up ´ zc yc = zc ´ xc zc = eye- center eye- center
View Transform view transform is translation into eye position, followed by rotation xc = up ´ zc up ´ zc yc = zc ´ xc compute 3 vectors:M zc = eye- center eye- center
View Transform view transform is translation into eye position, followed by rotation xc = up ´ zc up ´ zc yc = zc ´ xc compute 3 vectors:M zc = eye- center eye- center M = R×T(-e) = xx c xy c xz c 0 yx c yy c yz c 0 zx c zy c zz c 0 0 0 0 1 æ è ç ç ç ç ç ö ø ÷ ÷ ÷ ÷ ÷ 1 0 0 -eyex 0 1 0 -eyey 0 0 1 -eyez 0 0 0 1 æ è ç ç ç ç ç ö ø ÷ ÷ ÷ ÷ ÷
View Transform view transform is translation into eye position, followed by rotation M M = R×T(-e) = xx c xy c xz c - xx c eyex + xy c eyey + xz c eyez( ) yx c yy c yz c - yx c eyex + yy c eyey + yz c eyez( ) zx c zy c zz c - zx c eyex + zy c eyey + zz c eyez( ) 0 0 0 1 æ è ç ç ç ç ç ç ö ø ÷ ÷ ÷ ÷ ÷ ÷
View Transform • in camera/view space, the camera is at the origin, looking into negative z • modelview matrix is combined model (rotations, translations, scales) and view matrix! https://www.ntu.edu.sg/home/ehchua/programming/opengl/CG_BasicsTheory.html
View Transform • in camera/view space, the camera is at the origin, looking into negative z vodacek.zvb.cz x x z z up e
Projection Transform • similar to choosing lens and sensor of camera – specify field of view and aspect https://www.ntu.edu.sg/home/ehchua/programming/opengl/CG_BasicsTheory.html
Projection Transform - Perspective Projection • fovy: vertical angle in degrees • aspect: ratio of width/height • zNear (n): near clipping plane (relative from cam) • zFar (f): far clipping plane (relative from cam) M proj = f aspect 0 0 0 0 f 0 0 0 0 n + f n - f 2× f ×n n - f 0 0 -1 0 æ è ç ç ç ç ç ç ç ö ø ÷ ÷ ÷ ÷ ÷ ÷ ÷ f = cot( fovy / 2) projection matrix (symmetric frustum)
Projection Transform - Perspective Projection more general: a perspective “frustum” (truncated pyramid) • left (l), right (r), bottom (b), top (t): corner coordinates on near clipping plane M proj = 2n r - l 0 r + l r - l 0 0 2n t - b t + b t - b 0 0 0 - f + n f - n -2× f ×n f - n 0 0 -1 0 æ è ç ç ç ç ç ç ç ç ö ø ÷ ÷ ÷ ÷ ÷ ÷ ÷ ÷ projection matrix (asymmetric frustum) perspective frustum
Modelview Projection Matrix • put it all together with 4x4 matrix multiplications! projection matrix modelview matrixvertex in clip space vclip = Mproj ×Mview ×Mmodel ×v = Mproj ×Mmv ×v
Clip Space https://www.ntu.edu.sg/home/ehchua/programming/opengl/CG_BasicsTheory.html
Normalized Device Coordinates (NDC) • not in previous illustration • get to NDC by perspective division from: OpenGL Programming Guide vclip = xclip yclip zclip wclip æ è ç ç ç ç ç ö ø ÷ ÷ ÷ ÷ ÷ vNDC = xclip / wclip yclip / wclip zclip / wclip 1 æ è ç ç ç ç ç ö ø ÷ ÷ ÷ ÷ ÷ vertex in clip space vertex in NDC
Viewport Transform • also in matrix form (let’s skip the details) from: OpenGL Programming Guide vNDC = xclip / wclip yclip / wclip zclip / wclip 1 æ è ç ç ç ç ç ö ø ÷ ÷ ÷ ÷ ÷ vertex in NDC vwindow = xwindow ywindow zwindow 1 æ è ç ç ç ç ö ø ÷ ÷ ÷ ÷ Î 0,win_width -1( ) Î 0,win_height -1( ) Î 0,1( ) vertex in window coords
Section Overview • The graphics pipeline • Coordinate Space transformations • Shaders • Stereo rendering • View matrix • Projection matrix • Lens distortion • Fragment shader • Vertex shader
Shading! https://www.ntu.edu.sg/home/ehchua/programming/opengl/CG_BasicsTheory.html
Shading! https://www.ntu.edu.sg/home/ehchua/programming/opengl/CG_BasicsTheory.html
Vertex and Fragment Shaders • shaders are small programs that are executed in parallel on the GPU for each vertex (vertex shader) or each fragment (fragment shader) • vertex shader: • modelview projection transform of vertex & normal (see last lecture) • if per-vertex lighting: do lighting calculations here (otherwise omit) • fragment shader: • assign final color to each fragment • if per-fragment lighting: do all lighting calculations here (otherwise omit)
Shading! https://www.ntu.edu.sg/home/ehchua/programming/opengl/CG_BasicsTheory.html vertex shader fragment shader • Transforms • (per-vertex) lens distortion • (per-vertex) lighting • Texturing • (per-fragment) lens distortion • (per-fragment) lighting
Vertex Shaders https://www.ntu.edu.sg/home/ehchua/programming/opengl/CG_BasicsTheory.html vertex shader (executed for each vertex)input output • vertex position, normal, color, material, texture coordinates • modelview matrix, projection matrix, normal matrix • … • transformed vertex position (in clip coords), texture coordinates • … void main () { // do something here … }
Fragment Shaders https://www.ntu.edu.sg/home/ehchua/programming/opengl/CG_BasicsTheory.html input output • vertex position in window coords, texture coordinates • … • fragment color • fragment depth • … void main () { // do something here … } fragment shader (executed for each fragment)
Why Do We Need Shaders? • massively parallel computing • single instruction multiple data (SIMD) paradigm  GPUs are designed to be parallel processors • vertex shaders are independently executed for each vertex on GPU (in parallel) • fragment shaders are independently executed for each fragment on GPU (in parallel)
• most important: vertex transforms and lighting & shading calculations • shading: how to compute color of each fragment (e.g. interpolate colors) 1. Flat shading 2. Gouraud shading (per-vertex shading) 3. Phong shading (per-fragment shading) • other: render motion blur, depth of field, physical simulation, … courtesy: Intergraph Computer Systems Why Do We Need Shaders?
Shading Languages • Cg (C for Graphics – NVIDIA, deprecated) • GLSL (GL Shading Language – OpenGL) • HLSL (High Level Shading Language - MS Direct3D)
OpenGL Shading Language (GLSL) • high-level programming language for shaders • syntax similar to C (i.e. has main function and many other similarities) • usually very short programs that are executed in parallel on GPU • good introduction / tutorial: https://www.opengl.org/sdk/docs/tutorials/TyphoonLabs/
• versions of OpenGL, WebGL, GLSL can get confusing • here’s what we use: • WebGL 1.0 - based on OpenGL ES 2.0 • GLSL 1.10 - shader preprocessor: #version 110 • reason: three.js doesn’t support WebGL 2.0 yet OpenGL Shading Language (GLSL)
Section Overview • The graphics rendering pipeline • Coordinate Space transformations • Shaders • Stereo rendering • View matrix • Projection matrix • Lens distortion • Fragment shader • Vertex shader
Depth Perception monocular cues • perspective • relative object size • absolute size • occlusion • accommodation • retinal blur • motion parallax • texture gradients • shading • … wikipedia binocular cues • (con)vergence • disparity / parallax • …
binocular disparity motion parallax accommodation/blurconvergence current glasses-based (stereoscopic) displays near-term: light field displays longer-term: holographic displays Depth Perception
Depth Perception Cutting&Vishton,1995
Walker, Lewis E., 1865. Hon. Abraham Lincoln, President of the United States. Library of CongressCharles Wheatstone., 1841. Stereoscope. Stereoscopic Displays
Stereoscopic Displays
Parallax • parallax is the relative distance of a 3D point projected into the 2 stereo images case 1 case 2 case 3 http://paulbourke.net/stereographics/stereorender/
Parallax • visual system only uses horizontal parallax, no vertical parallax! • naïve toe-in method creates vertical parallax  visual discomfort Toe-in = incorrect! Off-axis = correct! http://paulbourke.net/stereographics/stereorender/
Parallax – well done
Parallax – well done 1862 “Tending wounded Union soldiers at Savage's Station, Virginia, during the Peninsular Campaign”, Library of Congress Prints and Photographs Division
Parallax – not well done
All Current-generation VR HMDs are “Simple Magnifiers” Stereo Rendering for HMDs
Image Formation HMD lens Side View micro display
Image Formation HMD lens Side View deye eye relief micro display f d' h'
Image Formation HMD virtual image Side View d h deye eye relief lens micro display f d' h'
Image Formation HMD virtual image Side View d 1 d + 1 d' = 1 f Û d = 1 1 f - 1 d' Gaussian thin lens formula: h deye eye relief lens micro display f d' h'
Image Formation HMD virtual image Side View d 1 d + 1 d' = 1 f Û d = 1 1 f - 1 d' Gaussian thin lens formula: Magnification: M = f f - d' Þ h = Mh' h deye eye relief lens micro display f d' h'
Stereo Rendering with OpenGL/WebGL • Only need to modify 2 steps in the pipeline! • View matrix • Projection matrix • Need to render two images now (one per eye), instead of just one • Render one eye at a time, to a different part of the screen
Stereo Rendering with OpenGL/WebGL • Only need to modify 2 steps in the pipeline! • View matrix • Projection matrix • Need to render two images now (one per eye), instead of just one • Render one eye at a time, to a different part of the screen
Stereo Rendering with OpenGL/WebGL • Only need to modify 2 steps in the pipeline! • View matrix • Projection matrix • Need to render two images now (one per eye), instead of just one • Render one eye at a time, to a different part of the screen
Stereo Rendering with OpenGL/WebGL • Only need to modify 2 steps in the pipeline! • View matrix • Projection matrix • Need to render two images now (one per eye), instead of just one • Render one eye at a time, to a different part of the screen
𝑀 = 𝑅 ∙ 𝑇(−𝑒) Adjusting the View Matrix
𝑀 = 𝑅 ∙ 𝑇(−𝑒) Adjusting the View Matrix
𝑀 = 𝑅 ∙ 𝑇(−𝑒) Adjusting the View Matrix
𝑀 = 𝑅 ∙ 𝑇(−𝑒) Adjusting the View Matrix
IPD 𝑀 = 𝑅 ∙ 𝑇(−𝑒) Adjusting the View Matrix
IPD 𝑀 = 𝑅 ∙ 𝑇(−𝑒) Z X Adjusting the View Matrix
IPD 𝑀 = 𝑅 ∙ 𝑇(−𝑒) Z X 𝑀𝐿/𝑅 = 𝑇 ±𝐼𝑃𝐷/2 0 0 𝑅 ∙ 𝑇(−𝑒) Adjusting the View Matrix
IPD Adjusting the View Matrix
IPD Adjusting the View Matrix
IPD Adjusting the View Matrix
IPD Adjusting the View Matrix
Adjusting the Projection Matrix
Image Formation HMD virtual image Side View d 1 d + 1 d' = 1 f Û d = 1 1 f - 1 d' Gaussian thin lens formula: Magnification: M = f f - d' Þ h = Mh' h deye eye relief lens micro display f d' h'
Image Formation virtual image Side View d h eye relief deye view frustum symmetric
Image Formation virtual image Side View d h eye relief deye view frustum symmetric near clipping plane
Image Formation virtual image Side View d h eye relief deye view frustum symmetric znear top bottom near clipping plane
Image Formation virtual image Side View d h eye relief deye view frustum symmetric znear top bottom similar triangles: near clipping plane top = znear h 2 d + deye( ) bottom = -znear h 2 d + deye( )
Image Formation Top View eye relief deye ipd d' w' HMD
Image Formation – Left Eye HMD Top View deye eye relief w' 2 ipd/2
HMD virtual image Top View d w1 deye eye relief w2 ipd/2 Image Formation – Left Eye
HMD virtual image Top View d w1 deye eye relief w2 w1 = M ipd 2 w2 = M w'- ipd 2 æ èç ö ø÷ ipd/2 Image Formation – Left Eye
virtual image Top View d eye relief deye view frustum asymmetric znear near clipping plane w1 w2 Image Formation – Left Eye
virtual image Top View d eye relief deye view frustum asymmetric znear right left near clipping plane w1 w2 Image Formation – Left Eye
virtual image Top View d eye relief deye view frustum asymmetric znear right left similar triangles: right = znear w1 d + deye left = -znear w2 d + deye near clipping plane w1 w2 Image Formation – Left Eye
virtual image Top View d eye relief deye view frustum asymmetric w1 w2 Image Formation – Right Eye w1 = M ipd 2 w2 = M w'- ipd 2 æ èç ö ø÷
virtual image Top View d eye relief deye view frustum asymmetric znear right left similar triangles: right = znear w2 d + deye left = -znear w1 d + deye w1 w2 Image Formation – Right Eye
Prototype Specs • ViewMaster VR Starter Pack (same specs as Google Cardboard 1): • lenses focal length: 45 mm • lenses diameter: 25 mm • interpupillary distance: 60 mm • distance between lenses and screen: 42 mm • Topfoison 6” LCD: width 132.5 mm, height 74.5 mm (1920x1080 pixels)
Image Formation • use these formulas to compute the perspective matrix in WebGL • you can use: THREE.Matrix4().makePerspective(left,right,top,bottom,near,far) THREE.Matrix4().lookAt(eye,center,up) • that’s all you need to render stereo images on the HMD
Image Formation for More Complex Optics • especially important in free-form optics, off-axis optical configurations & AR • use ray tracing – some nonlinear mapping from view frustum to microdisplay pixels • much more computationally challenging & sensitive to precise calibration; our HMD and most magnifier-based designs will work with what we discussed so far
Section Overview • The graphics pipeline • Coordinate Space transformations • Shaders • Stereo rendering • View matrix • Projection matrix • Lens distortion • Fragment shader • Vertex shader
All lenses introduce image distortion, chromatic aberrations, and other artifacts – we need to correct for them as best as we can in software!
image from: https://www.slideshare.net/Mark_Kilgard/nvidia-opengl-in-2016 • grid seen through HMD lens • lateral (xy) distortion of the image • chromatic aberrations: distortion is wavelength dependent! Lens Distortion
Pincussion Distortion Lens Distortion Barrel Distortion
Pincussion Distortion optical Lens Distortion Barrel Distortion digital correction
Lens Distortion image from: https://www.slideshare.net/Mark_Kilgard/nvidia-opengl-in-2016
Lens Distortion Barrel Distortion digital correction xu,yu
Lens Distortion Barrel Distortion digital correction xd » xu 1+ K1r2 + K2r4 ( ) yd » yu 1+ K1r2 + K2r4 ( ) xu,yu r2 = xu - xc( )2 + yu - yc( )2 undistorted point xc,yc radial distance from center center
Lens Distortion xd » xu 1+ K1r2 + K2r4 ( ) yd » yu 1+ K1r2 + K2r4 ( ) xu,yu r2 = xu - xc( )2 + yu - yc( )2 undistorted point xc,yc radial distance from center center NOTES: • center is assumed to be the center point (on optical axis) on screen (same as lookat center) • distortion is radially symmetric around center point = (0,0) • easy to get confused!
Lens Distortion – Center Point! Top View d h eye relief deye right eye xc,yc xc,yc left eye ipd
Lens Distortion Correction Example stereo rendering without lens distortion correction
Lens Distortion Correction Example stereo rendering with lens distortion correction
Where do we implement lens distortion correction? • End goal: move pixels around according to optical distortion parameters of the lenses
Where do we implement lens distortion correction? • End goal: move pixels around according to optical distortion parameters of the lenses https://www.ntu.edu.sg/home/ehchua/programming/opengl/CG_BasicsTheory.html
Section Overview • The graphics rendering pipeline • Coordinate Space transformations • Shaders • Stereo rendering • View matrix • Projection matrix • Lens distortion • Fragment shader • Vertex shader
Section Overview Want to learn more? • https://stanford.edu/class/ee267/ • “Fundamentals of Computer Graphics”, Shirley and Marschner • The graphics rendering pipeline • Coordinate Space transformations • Shaders • Stereo rendering • View matrix • Projection matrix • Lens distortion • Fragment shader • Vertex shader

More Related Content

PPTX
Build Your Own VR Display Course - SIGGRAPH 2017: Part 1
byStanfordComputationalImaging
 
PPTX
Virtual Reality
byrenoy reji
 
PDF
Comp4010 Lecture4 AR Tracking and Interaction
byMark Billinghurst
 
PDF
Interesting difference of VR research-style between Japanese and French / 日仏V...
byAkihiko Shirai
 
PPT
Raskar Graphics Interface May05
byCamera Culture Group, MIT Media Lab
 
PPTX
VR- virtual reality
byLakshmi Narayanan S
 
PDF
MHIT603: Lecture 4 - Experience Prototyping
byMark Billinghurst
 
PDF
426 lecture3: AR Tracking
byMark Billinghurst
 
Build Your Own VR Display Course - SIGGRAPH 2017: Part 1
byStanfordComputationalImaging
 
Virtual Reality
byrenoy reji
 
Comp4010 Lecture4 AR Tracking and Interaction
byMark Billinghurst
 
Interesting difference of VR research-style between Japanese and French / 日仏V...
byAkihiko Shirai
 
Raskar Graphics Interface May05
byCamera Culture Group, MIT Media Lab
 
VR- virtual reality
byLakshmi Narayanan S
 
MHIT603: Lecture 4 - Experience Prototyping
byMark Billinghurst
 
426 lecture3: AR Tracking
byMark Billinghurst
 

What's hot

PDF
COMP 4010: Lecture8 - AR Technology
byMark Billinghurst
 
PDF
COMP 4010 Lecture9 AR Displays
byMark Billinghurst
 
PDF
COMP 4010 Lecture5 VR Audio and Tracking
byMark Billinghurst
 
PDF
Lecture 6 Interaction Design for VR
byMark Billinghurst
 
PPT
Natural Interfaces for Augmented Reality
byMark Billinghurst
 
PDF
Introduction to Augmented Reality
byMark Billinghurst
 
PDF
MHIT 603: Introduction to Interaction Design
byMark Billinghurst
 
PPT
Raskar Graphics Interface May05 Web
byCamera Culture Group, MIT Media Lab
 
PPTX
CES 2018 VRAR
byJames D.B. Wang, PhD
 
PPT
Mark newburn
byNishanthi Bheeman
 
PDF
A Survey of Augmented Reality
byMark Billinghurst
 
PDF
Head Mounted Displays: How to realize ultimate AR experiences?
byYutaItoh
 
PDF
Culture meet network 2010 hung
byCulture Mondo Network Asia-Pacific Secretariat
 
PDF
MetaZtron holographic Z depth factor
byDiane Troyer
 
PDF
Hive Holographic Immersive Virutal Laser Projector Troyer
byDiane Troyer
 
PPTX
Laser projector opportunity (MetaZtron Vision)
byDiane Troyer
 
PDF
Introduction to Optical See-Through HMDs in AR
byYuta Itoh
 
PDF
COMP 4010: Lecture 4 - 3D User Interfaces for VR
byMark Billinghurst
 
PDF
MetatonZ: Troyer Patents Elevator uptodate 60614
byDiane Troyer
 
PDF
Metatroy Z*TV patents blogs Nov. 2011 - June 2012
byDiane Troyer
 
COMP 4010: Lecture8 - AR Technology
byMark Billinghurst
 
COMP 4010 Lecture9 AR Displays
byMark Billinghurst
 
COMP 4010 Lecture5 VR Audio and Tracking
byMark Billinghurst
 
Lecture 6 Interaction Design for VR
byMark Billinghurst
 
Natural Interfaces for Augmented Reality
byMark Billinghurst
 
Introduction to Augmented Reality
byMark Billinghurst
 
MHIT 603: Introduction to Interaction Design
byMark Billinghurst
 
Raskar Graphics Interface May05 Web
byCamera Culture Group, MIT Media Lab
 
CES 2018 VRAR
byJames D.B. Wang, PhD
 
Mark newburn
byNishanthi Bheeman
 
A Survey of Augmented Reality
byMark Billinghurst
 
Head Mounted Displays: How to realize ultimate AR experiences?
byYutaItoh
 
Culture meet network 2010 hung
byCulture Mondo Network Asia-Pacific Secretariat
 
MetaZtron holographic Z depth factor
byDiane Troyer
 
Hive Holographic Immersive Virutal Laser Projector Troyer
byDiane Troyer
 
Laser projector opportunity (MetaZtron Vision)
byDiane Troyer
 
Introduction to Optical See-Through HMDs in AR
byYuta Itoh
 
COMP 4010: Lecture 4 - 3D User Interfaces for VR
byMark Billinghurst
 
MetatonZ: Troyer Patents Elevator uptodate 60614
byDiane Troyer
 
Metatroy Z*TV patents blogs Nov. 2011 - June 2012
byDiane Troyer
 

Similar to Build Your Own VR Display Course - SIGGRAPH 2017: Part 2

PDF
ELEC4547_EmergingTechVRAR_Lecture_2_graphics.pdf
bypacopi9891
 
PPT
Computer Graphics involves technology to access. The Process transforms and p...
byErNandiniDharne
 
PPTX
chapter 3.pptxGeometry chapter 4 and 5 transformation ,translation ,animation...
byAntenehsolomon2
 
PPT
Bai 1
byChâu Thanh Chương
 
PDF
OpenGL L02-Transformations
byMohammad Shaker
 
PDF
Chapter-3.pdf
bymekelle university(EiT-M)
 
PDF
Open gl
byEU Edge
 
PPT
september11.ppt
byCharlesMatu2
 
PPTX
3 d graphics with opengl part 1
bySardar Alam
 
PPTX
3 CG_U1_P2_PPT_3 OpenGL.pptx
byssuser255bf1
 
PPT
Introduction to OpenGL modern OpenGL program
bychaitanyabhosale16
 
PPT
Lec4
bySahil Dahiya
 
PDF
lectureAll-OpenGL-complete-Guide-Tutorial.pdf
bySanjeevSaharan5
 
PPTX
OpenGL basics
byMohammad Hosein Nemati
 
PDF
4 pipeline computer graphics
bycairo university
 
PPT
CS 354 Introduction
byMark Kilgard
 
PPTX
Task 2
byLewisB2013
 
PPT
CS 354 Object Viewing and Representation
byMark Kilgard
 
PPTX
GFX Part 5 - Introduction to Object Transformations in OpenGL ES
byPrabindh Sundareson
 
PPT
Praseed Pai
byBarcamp Kerala
 
ELEC4547_EmergingTechVRAR_Lecture_2_graphics.pdf
bypacopi9891
 
Computer Graphics involves technology to access. The Process transforms and p...
byErNandiniDharne
 
chapter 3.pptxGeometry chapter 4 and 5 transformation ,translation ,animation...
byAntenehsolomon2
 
Bai 1
byChâu Thanh Chương
 
OpenGL L02-Transformations
byMohammad Shaker
 
Chapter-3.pdf
bymekelle university(EiT-M)
 
Open gl
byEU Edge
 
september11.ppt
byCharlesMatu2
 
3 d graphics with opengl part 1
bySardar Alam
 
3 CG_U1_P2_PPT_3 OpenGL.pptx
byssuser255bf1
 
Introduction to OpenGL modern OpenGL program
bychaitanyabhosale16
 
Lec4
bySahil Dahiya
 
lectureAll-OpenGL-complete-Guide-Tutorial.pdf
bySanjeevSaharan5
 
OpenGL basics
byMohammad Hosein Nemati
 
4 pipeline computer graphics
bycairo university
 
CS 354 Introduction
byMark Kilgard
 
Task 2
byLewisB2013
 
CS 354 Object Viewing and Representation
byMark Kilgard
 
GFX Part 5 - Introduction to Object Transformations in OpenGL ES
byPrabindh Sundareson
 
Praseed Pai
byBarcamp Kerala
 

More from StanfordComputationalImaging

PDF
Gaze-Contingent Ocular Parallax Rendering for Virtual Reality
byStanfordComputationalImaging
 
PPTX
Autofocals: Evaluating Gaze-Contingent Eyeglasses for Presbyopes - Siggraph 2019
byStanfordComputationalImaging
 
PPTX
Non-line-of-sight Imaging with Partial Occluders and Surface Normals | TOG 2019
byStanfordComputationalImaging
 
PPTX
End-to-end Optimization of Cameras and Image Processing - SIGGRAPH 2018
byStanfordComputationalImaging
 
PPTX
Computational Near-eye Displays with Focus Cues - SID 2017 Seminar
byStanfordComputationalImaging
 
PPTX
Accommodation-invariant Computational Near-eye Displays - SIGGRAPH 2017
byStanfordComputationalImaging
 
PPTX
Build Your Own VR Display Course - SIGGRAPH 2017: Part 5
byStanfordComputationalImaging
 
PPTX
Build Your Own VR Display Course - SIGGRAPH 2017: Part 4
byStanfordComputationalImaging
 
PPTX
Build Your Own VR Display Course - SIGGRAPH 2017: Part 3
byStanfordComputationalImaging
 
PPTX
VR2.0: Making Virtual Reality Better Than Reality?
byStanfordComputationalImaging
 
PPTX
Multi-camera Time-of-Flight Systems | SIGGRAPH 2016
byStanfordComputationalImaging
 
PPTX
ProxImaL | SIGGRAPH 2016
byStanfordComputationalImaging
 
PPTX
Light Field, Focus-tunable, and Monovision Near-eye Displays | SID 2016
byStanfordComputationalImaging
 
PPTX
Adaptive Spectral Projection
byStanfordComputationalImaging
 
PPTX
The Light Field Stereoscope | SIGGRAPH 2015
byStanfordComputationalImaging
 
PPTX
Compressive Light Field Projection @ SIGGRAPH 2014
byStanfordComputationalImaging
 
PPTX
Vision-correcting Displays @ SIGGRAPH 2014
byStanfordComputationalImaging
 
Gaze-Contingent Ocular Parallax Rendering for Virtual Reality
byStanfordComputationalImaging
 
Autofocals: Evaluating Gaze-Contingent Eyeglasses for Presbyopes - Siggraph 2019
byStanfordComputationalImaging
 
Non-line-of-sight Imaging with Partial Occluders and Surface Normals | TOG 2019
byStanfordComputationalImaging
 
End-to-end Optimization of Cameras and Image Processing - SIGGRAPH 2018
byStanfordComputationalImaging
 
Computational Near-eye Displays with Focus Cues - SID 2017 Seminar
byStanfordComputationalImaging
 
Accommodation-invariant Computational Near-eye Displays - SIGGRAPH 2017
byStanfordComputationalImaging
 
Build Your Own VR Display Course - SIGGRAPH 2017: Part 5
byStanfordComputationalImaging
 
Build Your Own VR Display Course - SIGGRAPH 2017: Part 4
byStanfordComputationalImaging
 
Build Your Own VR Display Course - SIGGRAPH 2017: Part 3
byStanfordComputationalImaging
 
VR2.0: Making Virtual Reality Better Than Reality?
byStanfordComputationalImaging
 
Multi-camera Time-of-Flight Systems | SIGGRAPH 2016
byStanfordComputationalImaging
 
ProxImaL | SIGGRAPH 2016
byStanfordComputationalImaging
 
Light Field, Focus-tunable, and Monovision Near-eye Displays | SID 2016
byStanfordComputationalImaging
 
Adaptive Spectral Projection
byStanfordComputationalImaging
 
The Light Field Stereoscope | SIGGRAPH 2015
byStanfordComputationalImaging
 
Compressive Light Field Projection @ SIGGRAPH 2014
byStanfordComputationalImaging
 
Vision-correcting Displays @ SIGGRAPH 2014
byStanfordComputationalImaging
 

Recently uploaded

PDF
Model QP 2025 scheme Q &A- Module 1 and 2.pdf
bySURESHA V
 
PDF
Soil Compressibility (Elastic Settlement).pdf
byMahmoodKhalid11
 
PPTX
Designing Work for Humans, Not Machines: Human-Centered Maintenance Excellence
byMaintWiz Technologies Private Limited
 
PDF
Chad Ayach - An Accomplished Mechanical Engineer
byChad Ayach
 
PPTX
Fitting Infiltration Models to Infiltration using Excel (1).pptx
byTomNickoRivera1
 
PPTX
Origin of Soil and Grain Size with Introduction and explanation
byMahmoodKhalid11
 
PDF
Industrial Tools Manufacturers In India : Torso Tools
bytorsotools8
 
PPT
Integer , Goal and Non linear Programming Model
byOcheriCyril2
 
PDF
Shear Strength of Soil/Mohr Coulomb Failure Criteria-1.pdf
byMahmoodKhalid11
 
PPTX
Introduction to AI and Applications Module-4.pptx
byKalaiselviSubramania2
 
PPTX
This Bearing Didn’t Fail Suddenly — How Vibration Data Predicts Failure Month...
byMaintWiz Technologies Private Limited
 
PDF
0.39 Inch Micro-OLED Display 1024×768 XGA Panel Silicon OLED
bySyluxdisplay
 
PPTX
Theory to Practice of Unsaturated Soil Mechanics-1.pptx
byMahmoodKhalid11
 
PPTX
uADPF Topology_SFP requirements_locked slides.pptx
byMd Bellal Hossain
 
PPTX
Lubrication Neglect Causes More Downtime Than AI Ever Will Why Maintenance Fu...
byMaintWiz Technologies Private Limited
 
PDF
Module 4 python programming-1BPLCK105B-2025 by Dr.SV.pdf
bySURESHA V
 
PPTX
ISO 13485.2016 Awareness's Training material
byPrakashSivan
 
PPTX
Basic Volume Mass Relationship and unit weight as function of volumetric wate...
byMahmoodKhalid11
 
PPTX
How Does LNG Regasification Work | INOXCVA
byINOXCVA
 
PPTX
SketchUp Pro 2026 – Advanced 3D Modeling Software
byHoka Moka
 
Model QP 2025 scheme Q &A- Module 1 and 2.pdf
bySURESHA V
 
Soil Compressibility (Elastic Settlement).pdf
byMahmoodKhalid11
 
Designing Work for Humans, Not Machines: Human-Centered Maintenance Excellence
byMaintWiz Technologies Private Limited
 
Chad Ayach - An Accomplished Mechanical Engineer
byChad Ayach
 
Fitting Infiltration Models to Infiltration using Excel (1).pptx
byTomNickoRivera1
 
Origin of Soil and Grain Size with Introduction and explanation
byMahmoodKhalid11
 
Industrial Tools Manufacturers In India : Torso Tools
bytorsotools8
 
Integer , Goal and Non linear Programming Model
byOcheriCyril2
 
Shear Strength of Soil/Mohr Coulomb Failure Criteria-1.pdf
byMahmoodKhalid11
 
Introduction to AI and Applications Module-4.pptx
byKalaiselviSubramania2
 
This Bearing Didn’t Fail Suddenly — How Vibration Data Predicts Failure Month...
byMaintWiz Technologies Private Limited
 
0.39 Inch Micro-OLED Display 1024×768 XGA Panel Silicon OLED
bySyluxdisplay
 
Theory to Practice of Unsaturated Soil Mechanics-1.pptx
byMahmoodKhalid11
 
uADPF Topology_SFP requirements_locked slides.pptx
byMd Bellal Hossain
 
Lubrication Neglect Causes More Downtime Than AI Ever Will Why Maintenance Fu...
byMaintWiz Technologies Private Limited
 
Module 4 python programming-1BPLCK105B-2025 by Dr.SV.pdf
bySURESHA V
 
ISO 13485.2016 Awareness's Training material
byPrakashSivan
 
Basic Volume Mass Relationship and unit weight as function of volumetric wate...
byMahmoodKhalid11
 
How Does LNG Regasification Work | INOXCVA
byINOXCVA
 
SketchUp Pro 2026 – Advanced 3D Modeling Software
byHoka Moka
 

Build Your Own VR Display Course - SIGGRAPH 2017: Part 2

  • 1.
    Build Your OwnVR Display The Graphics Pipeline, Stereo Rendering, and Lens Distortion Robert Konrad Stanford University stanford.edu/class/ee267/
  • 2.
    Image courtesy ofRobo Recall
  • 3.
    Albrecht Dürer, “Underweysungder Messung mit dem Zirckel und Richtscheyt”, 1525
  • 4.
    Section Overview • Thegraphics rendering pipeline • Coordinate space transformations • Shaders • Stereo rendering • View matrix • Projection matrix • Lens distortion • Fragment shader • Vertex shader
  • 5.
    WebGL • JavaScript applicationprogrammer interface (API) for 2D and 3D graphics • OpenGL ES 2.0 running in the browser, implemented by all modern browsers
  • 6.
    WebGL • JavaScript applicationprogrammer interface (API) for 2D and 3D graphics • OpenGL ES 2.0 running in the browser, implemented by all modern browsers
  • 7.
    WebGL • JavaScript applicationprogrammer interface (API) for 2D and 3D graphics • OpenGL ES 2.0 running in the browser, implemented by all modern browsers
  • 8.
    WebGL • JavaScript applicationprogrammer interface (API) for 2D and 3D graphics • OpenGL ES 2.0 running in the browser, implemented by all modern browsers
  • 9.
    WebGL • JavaScript applicationprogrammer interface (API) for 2D and 3D graphics • OpenGL ES 2.0 running in the browser, implemented by all modern browsers
  • 10.
    WebGL • JavaScript applicationprogrammer interface (API) for 2D and 3D graphics • OpenGL ES 2.0 running in the browser, implemented by all modern browsers
  • 11.
    three.js • cross-browser JavaScriptlibrary/API • higher-level library that provides a lot of useful helper functions, tools, and abstractions around WebGL – easy and convenient to use • https://threejs.org/ • simple examples: https://threejs.org/examples/ • great introduction (in WebGL): http://davidscottlyons.com/threejs/presentations/frontporch14/
  • 12.
    Computer Graphics! • atthe most basic level: conversion from 3D scene description to 2D image • what do you need to describe a static scene? • 3D geometry and transformations • lights • material properties / textures • Represent object surfaces as a set of primitive shapes • Points / Lines / Triangles / Quad (rilateral) s
  • 13.
  • 14.
    The Graphics Pipeline https://www.ntu.edu.sg/home/ehchua/programming/opengl/CG_BasicsTheory.html 1.Vertex Processing: Process and transform individual vertices with attributes (position, color, vertex normals, texture coordinates, etc.)
  • 15.
    The Graphics Pipeline https://www.ntu.edu.sg/home/ehchua/programming/opengl/CG_BasicsTheory.html 1.Vertex Processing: Process and transform individual vertices with attributes (position, color, vertex normals, texture coordinates, etc.) 2. Rasterization: Convert each primitive (connected vertices) into a set of fragments. A fragment can be treated as a pixel in 3D spaces, which is aligned with the pixel grid, with attributes interpolated from the vertices.
  • 16.
    The Graphics Pipeline https://www.ntu.edu.sg/home/ehchua/programming/opengl/CG_BasicsTheory.html 1.Vertex Processing: Process and transform individual vertices with attributes (position, color, vertex normals, texture coordinates, etc.) 2. Rasterization: Convert each primitive (connected vertices) into a set of fragments. A fragment can be treated as a pixel in 3D spaces, which is aligned with the pixel grid, with attributes interpolated from the vertices. 3. Fragment Processing: Process individual fragments.
  • 17.
    The Graphics Pipeline https://www.ntu.edu.sg/home/ehchua/programming/opengl/CG_BasicsTheory.html 1.Vertex Processing: Process and transform individual vertices with attributes (position, color, vertex normals, texture coordinates, etc.) 2. Rasterization: Convert each primitive (connected vertices) into a set of fragments. A fragment can be treated as a pixel in 3D spaces, which is aligned with the pixel grid, with attributes interpolated from the vertices. 3. Fragment Processing: Process individual fragments. 4. Output Merging: Combine the fragments of all primitives (in 3D space) into 2D color-pixel for the display.
  • 18.
    Coordinate Systems • righthand coordinate system • a few different coordinate systems: • object coordinates • world coordinates • viewing coordinates • also clip, normalized device, and window coordinates wikipedia
  • 19.
  • 20.
  • 21.
    Vertex Transforms https://www.ntu.edu.sg/home/ehchua/programming/opengl/CG_BasicsTheory.html 1. Arrangethe objects (or models, or avatar) in the world (Model Transformation or World transformation).
  • 22.
    Vertex Transforms https://www.ntu.edu.sg/home/ehchua/programming/opengl/CG_BasicsTheory.html 1. Arrangethe objects (or models, or avatar) in the world (Model Transformation or World transformation). 2. Position and orientation the camera (View transformation).
  • 23.
    Vertex Transforms https://www.ntu.edu.sg/home/ehchua/programming/opengl/CG_BasicsTheory.html 1. Arrangethe objects (or models, or avatar) in the world (Model Transformation or World transformation). 2. Position and orientation the camera (View transformation). 3. Select a camera lens (wide angle, normal or telescopic), adjust the focus length and zoom factor to set the camera's field of view (Projection transformation).
  • 24.
    Vertex Transforms https://www.ntu.edu.sg/home/ehchua/programming/opengl/CG_BasicsTheory.html 1. Arrangethe objects (or models, or avatar) in the world (Model Transformation or World transformation). 2. Position and orientation the camera (View transformation). 3. Select a camera lens (wide angle, normal or telescopic), adjust the focus length and zoom factor to set the camera's field of view (Projection transformation). 4. Print the photo on a selected area of the paper (Viewport transformation) - in rasterization stage
  • 25.
    Model Transform • transformeach vertex from object coordinates to world coordinates https://www.ntu.edu.sg/home/ehchua/programming/opengl/CG_BasicsTheory.html v = x y z æ è ç ç ç ö ø ÷ ÷ ÷
  • 26.
    Summary of HomogeneousMatrix Transforms • translation • scale • rotation Rx = 1 0 0 0 0 cosq -sinq 0 0 sinq cosq 0 0 0 0 1 æ è ç ç ç ç ö ø ÷ ÷ ÷ ÷ Ry = cosq 0 sinq 0 0 1 0 0 -sinq 0 cosq 0 0 0 0 1 æ è ç ç ç ç ö ø ÷ ÷ ÷ ÷ Read more: https://www.ntu.edu.sg/home/ehchua/programming/opengl/CG_BasicsTheory.html T(d) = 1 0 0 dx 0 1 0 dy 0 0 1 dz 0 0 0 1 æ è ç ç ç ç ç ö ø ÷ ÷ ÷ ÷ ÷ S(s) = sx 0 0 0 0 sy 0 0 0 0 sz 0 0 0 0 1 æ è ç ç ç ç ç ö ø ÷ ÷ ÷ ÷ ÷ Rz (q) = cosq -sinq 0 0 sinq cosq 0 0 0 0 1 0 0 0 0 1 æ è ç ç ç ç ö ø ÷ ÷ ÷ ÷
  • 27.
    Summary of HomogeneousMatrix Transforms • translation inverse translation • scale inverse scale • rotation inverse rotation T(d) = 1 0 0 dx 0 1 0 dy 0 0 1 dz 0 0 0 1 æ è ç ç ç ç ç ö ø ÷ ÷ ÷ ÷ ÷ S(s) = sx 0 0 0 0 sy 0 0 0 0 sz 0 0 0 0 1 æ è ç ç ç ç ç ö ø ÷ ÷ ÷ ÷ ÷ Rz (q) = cosq -sinq 0 0 sinq cosq 0 0 0 0 1 0 0 0 0 1 æ è ç ç ç ç ö ø ÷ ÷ ÷ ÷ Read more: https://www.ntu.edu.sg/home/ehchua/programming/opengl/CG_BasicsTheory.html T -1 (d) = T(-d) = 1 0 0 -dx 0 1 0 -dy 0 0 1 -dz 0 0 0 1 æ è ç ç ç ç ç ö ø ÷ ÷ ÷ ÷ ÷ S-1 (s) = S 1 s æ èç ö ø÷ = 1/ sx 0 0 0 0 1/ sy 0 0 0 0 1/ sz 0 0 0 0 1 æ è ç ç ç ç ç ö ø ÷ ÷ ÷ ÷ ÷ Rz -1 (q) = Rz -q( ) = cos-q -sin-q 0 0 sin-q cos-q 0 0 0 0 1 0 0 0 0 1 æ è ç ç ç ç ö ø ÷ ÷ ÷ ÷
  • 28.
    Summary of HomogeneousMatrix Transforms • successive transforms: • inverse successive transforms: v' = T ×S×Rz ×Rx ×T ×v Read more: https://www.ntu.edu.sg/home/ehchua/programming/opengl/CG_BasicsTheory.html v = T ×S× Rz × Rx ×T( ) -1 ×v' = T -1 × Rx -1 × Rz -1 ×S-1 ×T -1 ×v'
  • 29.
    Attention! • rotations andtranslations (or transforms in general) are not commutative! • make sure you get the correct order!
  • 30.
    View Transform • sofar we discussed model transforms, e.g. going from object or model space to world space https://www.ntu.edu.sg/home/ehchua/programming/opengl/CG_BasicsTheory.html
  • 31.
    View Transform • sofar we discussed model transforms, e.g. going from object or model space to world space • one simple 4x4 transform matrix is sufficient to go from world space to camera or view space! https://www.ntu.edu.sg/home/ehchua/programming/opengl/CG_BasicsTheory.html
  • 32.
    View Transform specify cameraby • eye position • reference position • up vector eye = eyex eyey eyez æ è ç ç ç ö ø ÷ ÷ ÷ up = upx upy upz æ è ç ç ç ö ø ÷ ÷ ÷ center = centerx centery centerz æ è ç ç ç ö ø ÷ ÷ ÷
  • 33.
    View Transform specify cameraby • eye position • reference position • up vector up = upx upy upz æ è ç ç ç ö ø ÷ ÷ ÷ center = centerx centery centerz æ è ç ç ç ö ø ÷ ÷ ÷ compute 3 vectors: eye = eyex eyey eyez æ è ç ç ç ö ø ÷ ÷ ÷ xc = up ´ zc up ´ zc yc = zc ´ xc zc = eye- center eye- center
  • 34.
    View Transform view transformis translation into eye position, followed by rotation xc = up ´ zc up ´ zc yc = zc ´ xc compute 3 vectors:M zc = eye- center eye- center
  • 35.
    View Transform view transformis translation into eye position, followed by rotation xc = up ´ zc up ´ zc yc = zc ´ xc compute 3 vectors:M zc = eye- center eye- center M = R×T(-e) = xx c xy c xz c 0 yx c yy c yz c 0 zx c zy c zz c 0 0 0 0 1 æ è ç ç ç ç ç ö ø ÷ ÷ ÷ ÷ ÷ 1 0 0 -eyex 0 1 0 -eyey 0 0 1 -eyez 0 0 0 1 æ è ç ç ç ç ç ö ø ÷ ÷ ÷ ÷ ÷
  • 36.
    View Transform view transformis translation into eye position, followed by rotation M M = R×T(-e) = xx c xy c xz c - xx c eyex + xy c eyey + xz c eyez( ) yx c yy c yz c - yx c eyex + yy c eyey + yz c eyez( ) zx c zy c zz c - zx c eyex + zy c eyey + zz c eyez( ) 0 0 0 1 æ è ç ç ç ç ç ç ö ø ÷ ÷ ÷ ÷ ÷ ÷
  • 37.
    View Transform • incamera/view space, the camera is at the origin, looking into negative z • modelview matrix is combined model (rotations, translations, scales) and view matrix! https://www.ntu.edu.sg/home/ehchua/programming/opengl/CG_BasicsTheory.html
  • 38.
    View Transform • incamera/view space, the camera is at the origin, looking into negative z vodacek.zvb.cz x x z z up e
  • 39.
    Projection Transform • similarto choosing lens and sensor of camera – specify field of view and aspect https://www.ntu.edu.sg/home/ehchua/programming/opengl/CG_BasicsTheory.html
  • 40.
    Projection Transform -Perspective Projection • fovy: vertical angle in degrees • aspect: ratio of width/height • zNear (n): near clipping plane (relative from cam) • zFar (f): far clipping plane (relative from cam) M proj = f aspect 0 0 0 0 f 0 0 0 0 n + f n - f 2× f ×n n - f 0 0 -1 0 æ è ç ç ç ç ç ç ç ö ø ÷ ÷ ÷ ÷ ÷ ÷ ÷ f = cot( fovy / 2) projection matrix (symmetric frustum)
  • 41.
    Projection Transform -Perspective Projection more general: a perspective “frustum” (truncated pyramid) • left (l), right (r), bottom (b), top (t): corner coordinates on near clipping plane M proj = 2n r - l 0 r + l r - l 0 0 2n t - b t + b t - b 0 0 0 - f + n f - n -2× f ×n f - n 0 0 -1 0 æ è ç ç ç ç ç ç ç ç ö ø ÷ ÷ ÷ ÷ ÷ ÷ ÷ ÷ projection matrix (asymmetric frustum) perspective frustum
  • 42.
    Modelview Projection Matrix •put it all together with 4x4 matrix multiplications! projection matrix modelview matrixvertex in clip space vclip = Mproj ×Mview ×Mmodel ×v = Mproj ×Mmv ×v
  • 43.
  • 44.
    Normalized Device Coordinates(NDC) • not in previous illustration • get to NDC by perspective division from: OpenGL Programming Guide vclip = xclip yclip zclip wclip æ è ç ç ç ç ç ö ø ÷ ÷ ÷ ÷ ÷ vNDC = xclip / wclip yclip / wclip zclip / wclip 1 æ è ç ç ç ç ç ö ø ÷ ÷ ÷ ÷ ÷ vertex in clip space vertex in NDC
  • 45.
    Viewport Transform • alsoin matrix form (let’s skip the details) from: OpenGL Programming Guide vNDC = xclip / wclip yclip / wclip zclip / wclip 1 æ è ç ç ç ç ç ö ø ÷ ÷ ÷ ÷ ÷ vertex in NDC vwindow = xwindow ywindow zwindow 1 æ è ç ç ç ç ö ø ÷ ÷ ÷ ÷ Î 0,win_width -1( ) Î 0,win_height -1( ) Î 0,1( ) vertex in window coords
  • 46.
    Section Overview • Thegraphics pipeline • Coordinate Space transformations • Shaders • Stereo rendering • View matrix • Projection matrix • Lens distortion • Fragment shader • Vertex shader
  • 47.
  • 48.
  • 49.
    Vertex and FragmentShaders • shaders are small programs that are executed in parallel on the GPU for each vertex (vertex shader) or each fragment (fragment shader) • vertex shader: • modelview projection transform of vertex & normal (see last lecture) • if per-vertex lighting: do lighting calculations here (otherwise omit) • fragment shader: • assign final color to each fragment • if per-fragment lighting: do all lighting calculations here (otherwise omit)
  • 50.
    Shading! https://www.ntu.edu.sg/home/ehchua/programming/opengl/CG_BasicsTheory.html vertex shader fragmentshader • Transforms • (per-vertex) lens distortion • (per-vertex) lighting • Texturing • (per-fragment) lens distortion • (per-fragment) lighting
  • 51.
    Vertex Shaders https://www.ntu.edu.sg/home/ehchua/programming/opengl/CG_BasicsTheory.html vertex shader(executed for each vertex)input output • vertex position, normal, color, material, texture coordinates • modelview matrix, projection matrix, normal matrix • … • transformed vertex position (in clip coords), texture coordinates • … void main () { // do something here … }
  • 52.
    Fragment Shaders https://www.ntu.edu.sg/home/ehchua/programming/opengl/CG_BasicsTheory.html input output •vertex position in window coords, texture coordinates • … • fragment color • fragment depth • … void main () { // do something here … } fragment shader (executed for each fragment)
  • 53.
    Why Do WeNeed Shaders? • massively parallel computing • single instruction multiple data (SIMD) paradigm  GPUs are designed to be parallel processors • vertex shaders are independently executed for each vertex on GPU (in parallel) • fragment shaders are independently executed for each fragment on GPU (in parallel)
  • 54.
    • most important:vertex transforms and lighting & shading calculations • shading: how to compute color of each fragment (e.g. interpolate colors) 1. Flat shading 2. Gouraud shading (per-vertex shading) 3. Phong shading (per-fragment shading) • other: render motion blur, depth of field, physical simulation, … courtesy: Intergraph Computer Systems Why Do We Need Shaders?
  • 55.
    Shading Languages • Cg(C for Graphics – NVIDIA, deprecated) • GLSL (GL Shading Language – OpenGL) • HLSL (High Level Shading Language - MS Direct3D)
  • 56.
    OpenGL Shading Language(GLSL) • high-level programming language for shaders • syntax similar to C (i.e. has main function and many other similarities) • usually very short programs that are executed in parallel on GPU • good introduction / tutorial: https://www.opengl.org/sdk/docs/tutorials/TyphoonLabs/
  • 57.
    • versions ofOpenGL, WebGL, GLSL can get confusing • here’s what we use: • WebGL 1.0 - based on OpenGL ES 2.0 • GLSL 1.10 - shader preprocessor: #version 110 • reason: three.js doesn’t support WebGL 2.0 yet OpenGL Shading Language (GLSL)
  • 58.
    Section Overview • Thegraphics rendering pipeline • Coordinate Space transformations • Shaders • Stereo rendering • View matrix • Projection matrix • Lens distortion • Fragment shader • Vertex shader
  • 59.
    Depth Perception monocularcues • perspective • relative object size • absolute size • occlusion • accommodation • retinal blur • motion parallax • texture gradients • shading • … wikipedia binocular cues • (con)vergence • disparity / parallax • …
  • 60.
    binocular disparity motionparallax accommodation/blurconvergence current glasses-based (stereoscopic) displays near-term: light field displays longer-term: holographic displays Depth Perception
  • 61.
  • 62.
    Walker, Lewis E.,1865. Hon. Abraham Lincoln, President of the United States. Library of CongressCharles Wheatstone., 1841. Stereoscope. Stereoscopic Displays
  • 63.
  • 64.
    Parallax • parallax isthe relative distance of a 3D point projected into the 2 stereo images case 1 case 2 case 3 http://paulbourke.net/stereographics/stereorender/
  • 65.
    Parallax • visual systemonly uses horizontal parallax, no vertical parallax! • naïve toe-in method creates vertical parallax  visual discomfort Toe-in = incorrect! Off-axis = correct! http://paulbourke.net/stereographics/stereorender/
  • 66.
  • 67.
    Parallax – welldone 1862 “Tending wounded Union soldiers at Savage's Station, Virginia, during the Peninsular Campaign”, Library of Congress Prints and Photographs Division
  • 68.
  • 69.
    All Current-generation VRHMDs are “Simple Magnifiers” Stereo Rendering for HMDs
  • 70.
  • 71.
    Image Formation HMD lens Side View deye eyerelief micro display f d' h'
  • 72.
    Image Formation HMD virtual image SideView d h deye eye relief lens micro display f d' h'
  • 73.
    Image Formation HMD virtual image SideView d 1 d + 1 d' = 1 f Û d = 1 1 f - 1 d' Gaussian thin lens formula: h deye eye relief lens micro display f d' h'
  • 74.
    Image Formation HMD virtual image SideView d 1 d + 1 d' = 1 f Û d = 1 1 f - 1 d' Gaussian thin lens formula: Magnification: M = f f - d' Þ h = Mh' h deye eye relief lens micro display f d' h'
  • 75.
    Stereo Rendering withOpenGL/WebGL • Only need to modify 2 steps in the pipeline! • View matrix • Projection matrix • Need to render two images now (one per eye), instead of just one • Render one eye at a time, to a different part of the screen
  • 76.
    Stereo Rendering withOpenGL/WebGL • Only need to modify 2 steps in the pipeline! • View matrix • Projection matrix • Need to render two images now (one per eye), instead of just one • Render one eye at a time, to a different part of the screen
  • 77.
    Stereo Rendering withOpenGL/WebGL • Only need to modify 2 steps in the pipeline! • View matrix • Projection matrix • Need to render two images now (one per eye), instead of just one • Render one eye at a time, to a different part of the screen
  • 78.
    Stereo Rendering withOpenGL/WebGL • Only need to modify 2 steps in the pipeline! • View matrix • Projection matrix • Need to render two images now (one per eye), instead of just one • Render one eye at a time, to a different part of the screen
  • 79.
    𝑀 = 𝑅∙ 𝑇(−𝑒) Adjusting the View Matrix
  • 80.
    𝑀 = 𝑅∙ 𝑇(−𝑒) Adjusting the View Matrix
  • 81.
    𝑀 = 𝑅∙ 𝑇(−𝑒) Adjusting the View Matrix
  • 82.
    𝑀 = 𝑅∙ 𝑇(−𝑒) Adjusting the View Matrix
  • 83.
    IPD 𝑀 = 𝑅∙ 𝑇(−𝑒) Adjusting the View Matrix
  • 84.
    IPD 𝑀 = 𝑅∙ 𝑇(−𝑒) Z X Adjusting the View Matrix
  • 85.
    IPD 𝑀 = 𝑅∙ 𝑇(−𝑒) Z X 𝑀𝐿/𝑅 = 𝑇 ±𝐼𝑃𝐷/2 0 0 𝑅 ∙ 𝑇(−𝑒) Adjusting the View Matrix
  • 86.
  • 87.
  • 88.
  • 89.
  • 90.
  • 91.
    Image Formation HMD virtual image SideView d 1 d + 1 d' = 1 f Û d = 1 1 f - 1 d' Gaussian thin lens formula: Magnification: M = f f - d' Þ h = Mh' h deye eye relief lens micro display f d' h'
  • 92.
    Image Formation virtual image SideView d h eye relief deye view frustum symmetric
  • 93.
    Image Formation virtual image SideView d h eye relief deye view frustum symmetric near clipping plane
  • 94.
    Image Formation virtual image SideView d h eye relief deye view frustum symmetric znear top bottom near clipping plane
  • 95.
    Image Formation virtual image SideView d h eye relief deye view frustum symmetric znear top bottom similar triangles: near clipping plane top = znear h 2 d + deye( ) bottom = -znear h 2 d + deye( )
  • 96.
    Image Formation Top View eyerelief deye ipd d' w' HMD
  • 97.
    Image Formation –Left Eye HMD Top View deye eye relief w' 2 ipd/2
  • 98.
    HMD virtual image Top View d w1 deye eyerelief w2 ipd/2 Image Formation – Left Eye
  • 99.
    HMD virtual image Top View d w1 deye eyerelief w2 w1 = M ipd 2 w2 = M w'- ipd 2 æ èç ö ø÷ ipd/2 Image Formation – Left Eye
  • 100.
    virtual image Top View d eyerelief deye view frustum asymmetric znear near clipping plane w1 w2 Image Formation – Left Eye
  • 101.
    virtual image Top View d eyerelief deye view frustum asymmetric znear right left near clipping plane w1 w2 Image Formation – Left Eye
  • 102.
    virtual image Top View d eyerelief deye view frustum asymmetric znear right left similar triangles: right = znear w1 d + deye left = -znear w2 d + deye near clipping plane w1 w2 Image Formation – Left Eye
  • 103.
    virtual image Top View d eyerelief deye view frustum asymmetric w1 w2 Image Formation – Right Eye w1 = M ipd 2 w2 = M w'- ipd 2 æ èç ö ø÷
  • 104.
    virtual image Top View d eyerelief deye view frustum asymmetric znear right left similar triangles: right = znear w2 d + deye left = -znear w1 d + deye w1 w2 Image Formation – Right Eye
  • 105.
    Prototype Specs • ViewMasterVR Starter Pack (same specs as Google Cardboard 1): • lenses focal length: 45 mm • lenses diameter: 25 mm • interpupillary distance: 60 mm • distance between lenses and screen: 42 mm • Topfoison 6” LCD: width 132.5 mm, height 74.5 mm (1920x1080 pixels)
  • 106.
    Image Formation • usethese formulas to compute the perspective matrix in WebGL • you can use: THREE.Matrix4().makePerspective(left,right,top,bottom,near,far) THREE.Matrix4().lookAt(eye,center,up) • that’s all you need to render stereo images on the HMD
  • 107.
    Image Formation forMore Complex Optics • especially important in free-form optics, off-axis optical configurations & AR • use ray tracing – some nonlinear mapping from view frustum to microdisplay pixels • much more computationally challenging & sensitive to precise calibration; our HMD and most magnifier-based designs will work with what we discussed so far
  • 108.
    Section Overview • Thegraphics pipeline • Coordinate Space transformations • Shaders • Stereo rendering • View matrix • Projection matrix • Lens distortion • Fragment shader • Vertex shader
  • 109.
    All lenses introduceimage distortion, chromatic aberrations, and other artifacts – we need to correct for them as best as we can in software!
  • 110.
    image from: https://www.slideshare.net/Mark_Kilgard/nvidia-opengl-in-2016 •grid seen through HMD lens • lateral (xy) distortion of the image • chromatic aberrations: distortion is wavelength dependent! Lens Distortion
  • 111.
  • 112.
  • 113.
    Lens Distortion image from:https://www.slideshare.net/Mark_Kilgard/nvidia-opengl-in-2016
  • 114.
  • 115.
    Lens Distortion Barrel Distortion digitalcorrection xd » xu 1+ K1r2 + K2r4 ( ) yd » yu 1+ K1r2 + K2r4 ( ) xu,yu r2 = xu - xc( )2 + yu - yc( )2 undistorted point xc,yc radial distance from center center
  • 116.
    Lens Distortion xd »xu 1+ K1r2 + K2r4 ( ) yd » yu 1+ K1r2 + K2r4 ( ) xu,yu r2 = xu - xc( )2 + yu - yc( )2 undistorted point xc,yc radial distance from center center NOTES: • center is assumed to be the center point (on optical axis) on screen (same as lookat center) • distortion is radially symmetric around center point = (0,0) • easy to get confused!
  • 117.
    Lens Distortion –Center Point! Top View d h eye relief deye right eye xc,yc xc,yc left eye ipd
  • 118.
    Lens Distortion CorrectionExample stereo rendering without lens distortion correction
  • 119.
    Lens Distortion CorrectionExample stereo rendering with lens distortion correction
  • 120.
    Where do weimplement lens distortion correction? • End goal: move pixels around according to optical distortion parameters of the lenses
  • 121.
    Where do weimplement lens distortion correction? • End goal: move pixels around according to optical distortion parameters of the lenses https://www.ntu.edu.sg/home/ehchua/programming/opengl/CG_BasicsTheory.html
  • 122.
    Section Overview • Thegraphics rendering pipeline • Coordinate Space transformations • Shaders • Stereo rendering • View matrix • Projection matrix • Lens distortion • Fragment shader • Vertex shader
  • 123.
    Section Overview Want tolearn more? • https://stanford.edu/class/ee267/ • “Fundamentals of Computer Graphics”, Shirley and Marschner • The graphics rendering pipeline • Coordinate Space transformations • Shaders • Stereo rendering • View matrix • Projection matrix • Lens distortion • Fragment shader • Vertex shader