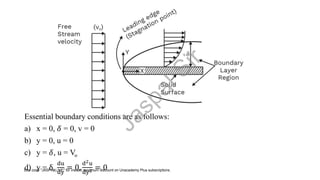
The document summarizes key concepts regarding boundary layer theory. Some key points include:
- Boundary layer theory describes fluid flow very close to a solid surface, where viscosity is important.
- In the boundary layer, velocity increases from zero at the surface to the free stream value over a thin region called the boundary layer thickness.
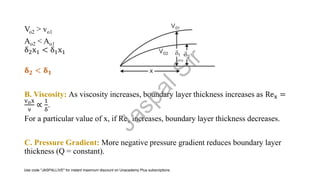
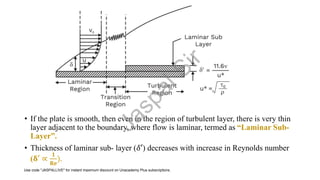
- Boundary layers can be laminar or turbulent, with turbulent layers having greater thickness. Transition from laminar to turbulent occurs due to instabilities.
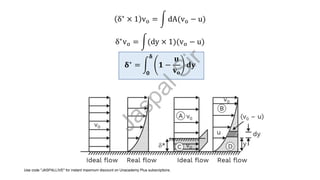
- Important parameters like displacement thickness, momentum thickness, and drag coefficients are defined. Blasius solutions provide relationships between boundary layer properties for simple cases.








![Q. Assertion (A): Boundary layer theory is applicable only in the vicinity of the
leading edge of the plate.
Reason (R): Boundary layer theory is based on the assumption that its thickness is
small when compared to other linear dimensions.
a) Assertion (A) and Reason (R) are individually true and Reason (R) is correct
explanation of Assertion (A)
b) Assertion (A) and Reason (R) are individually true but Reason (R) is not the
correct explanation of Assertion (A)
c) Assertion (A) is correct but Reason (R) is incorrect
d) Assertion (A) is incorrect but Reason (R) is correct.
[IES: 2006]
J
a
s
p
a
l
S
i
r
Use code "JASPALLIVE" for instant maximum discount on Unacademy Plus subscriptions.](https://image.slidesharecdn.com/fmchapter-11-230929214805-0c560f23/85/FM-chapter-11-pdf-12-320.jpg)


![Q. What is the momentum thickness for the boundary layer with velocity
distribution
u
U
=
y
δ
?
a) δ/6.
b) δ/2
c) 3 δ/2
d) 2 δ
[IES: 2008]
J
a
s
p
a
l
S
i
r
Use code "JASPALLIVE" for instant maximum discount on Unacademy Plus subscriptions.](https://image.slidesharecdn.com/fmchapter-11-230929214805-0c560f23/85/FM-chapter-11-pdf-16-320.jpg)
![Q. The displacement thickness of a boundary layer is
a) The distance to the point where (v/V) = 0.99
b) The distance where the velocity ‘v’ is equal to the shear velocity V*, that is,
where v = V*
c) The distance by which the main flow is to be shifted from the boundary to
maintain the continuity equation.
d) One- half the actual thickness of the boundary layer
[IES: 1997]
J
a
s
p
a
l
S
i
r
Use code "JASPALLIVE" for instant maximum discount on Unacademy Plus subscriptions.](https://image.slidesharecdn.com/fmchapter-11-230929214805-0c560f23/85/FM-chapter-11-pdf-17-320.jpg)



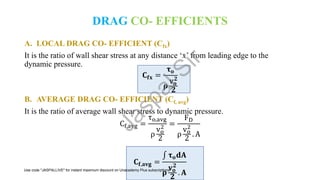

![NOTE: δ ∝ x Τ
4
5, hence boundary layer thickness increases more rapidly in
turbulent boundary layer than in laminar boundary layer.
Also,
𝐂𝐟𝐱 =
𝛕𝐨
𝛒𝐯𝐨
𝟐
𝟐
=
𝟎. 𝟎𝟓𝟗
𝐑𝐞𝐱
ൗ
𝟏
𝟓
; 𝟓 × 𝟏𝟎𝟓 < 𝐑𝐞 < 𝟏𝟎𝟕
𝐂𝐟𝐱 =
𝛕𝐨
𝛒𝐯𝐨
𝟐
𝟐
=
𝟎. 𝟑𝟕
[𝐥𝐨𝐠𝟏𝟎 𝐑𝐞𝐱 ]𝟐.𝟓𝟖
; 𝟏𝟎𝟕 < 𝐑𝐞 < 𝟏𝟎𝟗
NOTE: τo ∝
1
x ൗ
1
5
, hence boundary shear stress decreases less rapidly in turbulent
boundary layer than in laminar boundary layer.
J
a
s
p
a
l
S
i
r
Use code "JASPALLIVE" for instant maximum discount on Unacademy Plus subscriptions.](https://image.slidesharecdn.com/fmchapter-11-230929214805-0c560f23/85/FM-chapter-11-pdf-23-320.jpg)
![Also,
𝐂𝐟,𝐚𝐯𝐠 =
𝟎. 𝟎𝟕𝟗
𝐑𝐞𝐋
ൗ
𝟏
𝟓
; 𝟓 × 𝟏𝟎𝟓
< 𝐑𝐞 < 𝟏𝟎𝟕
𝐂𝐟,𝐚𝐯𝐠 =
𝟎. 𝟒𝟓𝟓
[𝐥𝐨𝐠𝟏𝟎 𝐑𝐞𝐋 ]𝟐.𝟓𝟖
; 𝟏𝟎𝟕 < 𝐑𝐞 < 𝟏𝟎𝟗
NOTE: All the above expressions are applicable only if turbulent boundary layer is
present throughout.
J
a
s
p
a
l
S
i
r
Use code "JASPALLIVE" for instant maximum discount on Unacademy Plus subscriptions.](https://image.slidesharecdn.com/fmchapter-11-230929214805-0c560f23/85/FM-chapter-11-pdf-24-320.jpg)
![Q. The ratio of the co- efficient of friction drag in laminar boundary layer compared
to that in turbulent boundary layer is proportional to
a) RL
1/2
b) RL
1/5
c) RL
3/10
d) RL
-3/10.
[IES: 1996]
J
a
s
p
a
l
S
i
r
Use code "JASPALLIVE" for instant maximum discount on Unacademy Plus subscriptions.](https://image.slidesharecdn.com/fmchapter-11-230929214805-0c560f23/85/FM-chapter-11-pdf-25-320.jpg)
![Q. If δ1 and δ2 are the laminar boundary layer thickness at a point M distant x from
the leading edge when the Reynolds number of the flow are 100 and 484,
respectively, then the ratio of
δ1
δ2
will be
a) 2.2.
b) 4.84
c) 23.43
d) 45.45
[IES: 2018]
J
a
s
p
a
l
S
i
r
Use code "JASPALLIVE" for instant maximum discount on Unacademy Plus subscriptions.](https://image.slidesharecdn.com/fmchapter-11-230929214805-0c560f23/85/FM-chapter-11-pdf-26-320.jpg)

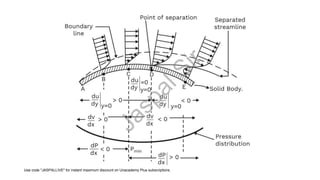


![Q. Flow separation is likely to occur when the pressure gradient is
a) Positive.
b) Zero
c) Negative
d) Negative and only when equal to -0.332
[GATE: 1992]
J
a
s
p
a
l
S
i
r
Use code "JASPALLIVE" for instant maximum discount on Unacademy Plus subscriptions.](https://image.slidesharecdn.com/fmchapter-11-230929214805-0c560f23/85/FM-chapter-11-pdf-31-320.jpg)
![Q. Which of the following is responsible for the separation of boundary layer?
a) Positive pressure gradient.
b) High viscosity of fluid
c) Low viscosity of fluid
d) None of these
[SSC: 2017]
J
a
s
p
a
l
S
i
r
Use code "JASPALLIVE" for instant maximum discount on Unacademy Plus subscriptions.](https://image.slidesharecdn.com/fmchapter-11-230929214805-0c560f23/85/FM-chapter-11-pdf-32-320.jpg)
![Q. Separation of flow occurs when pressure gradient
a) Tends to approach zero.
b) Becomes negative
c) Changes abruptly
d) Reduces to a value when vapor formation starts
[SSC: 2016]
J
a
s
p
a
l
S
i
r
Use code "JASPALLIVE" for instant maximum discount on Unacademy Plus subscriptions.](https://image.slidesharecdn.com/fmchapter-11-230929214805-0c560f23/85/FM-chapter-11-pdf-33-320.jpg)
![Q. Assertion: At the point of boundary layer separation, the shear stress is zero.
Reason (R): The point of separation demarcates between zones of forward and
reverse flow close to the wall.
a) Assertion (A) and Reason (R) are individually true and Reason (R) is correct
explanation of Assertion (A).
b) Assertion (A) and Reason (R) are individually true but Reason (R) is not the
correct explanation of Assertion (A)
c) Assertion (A) is correct but Reason (R) is incorrect
d) Assertion (A) is incorrect but Reason (R) is correct
[IES: 2011]
J
a
s
p
a
l
S
i
r
Use code "JASPALLIVE" for instant maximum discount on Unacademy Plus subscriptions.](https://image.slidesharecdn.com/fmchapter-11-230929214805-0c560f23/85/FM-chapter-11-pdf-34-320.jpg)
![Q. Consider the following statements:
The critical value of Reynolds number at which the boundary layer changes from
laminar to turbulent depends upon
1. Turbulence in ambient flow
2. Surface roughness
Which of the above statements is/ are correct?
a) Neither 1 nor 2
b) 1 only
c) 2 only
d) Both 1 and 2.
[IES: 2008]
J
a
s
p
a
l
S
i
r
Use code "JASPALLIVE" for instant maximum discount on Unacademy Plus subscriptions.](https://image.slidesharecdn.com/fmchapter-11-230929214805-0c560f23/85/FM-chapter-11-pdf-35-320.jpg)
![Q. Which one of the following assumptions in deriving the boundary layer equation
of flow past a flat plate at zero incidence is not correct?
a) Uniform flow = 0
b) Outside boundary layer velocity is vo throughout
c) The boundary layer thickness 𝛿 is very small compared to distance x
d) Pressure remains constant throughout the flow both within and outside the
boundary layer.
[IES: 2006]
J
a
s
p
a
l
S
i
r
Use code "JASPALLIVE" for instant maximum discount on Unacademy Plus subscriptions.](https://image.slidesharecdn.com/fmchapter-11-230929214805-0c560f23/85/FM-chapter-11-pdf-36-320.jpg)
![Q. Match List-I with List- II and select the correct answer:
Codes: A B C D
a) 1 2 3 4
b) 2 1 3 4
c) 1 2 4 3
d) 2 1 4 3.
[IES: 2002]
List- I List- II
A.
𝜕u
𝜕y y=0
is zero 1. The flow is attached flow
B.
𝜕u
𝜕y y=0
is positive 2. The flow is on the verge of separation
C. Displacement thickness 3. 0
δ u
U
1 −
u
U
dy
D. Momentum thickness 4. 0
δ
1 −
u
U
dy
J
a
s
p
a
l
S
i
r
Use code "JASPALLIVE" for instant maximum discount on Unacademy Plus subscriptions.](https://image.slidesharecdn.com/fmchapter-11-230929214805-0c560f23/85/FM-chapter-11-pdf-37-320.jpg)
![Q. A flat plate is kept in an infinite fluid medium. The fluid has a uniform free
stream velocity parallel to the plate. For the laminar boundary layer formed on the
plate, pick the correct option matching List- I and List- II.
Codes: A B C
a) 1 2 3
b) 2 2 2
c) 1 1 2
d) 2 1 3.
[GATE: 2003]
List- I List- II
A. Boundary layer thickness 1. Decreases in the flow direction
B. Shear stress at the plate 2. Increases in the flow direction
C. Pressure gradient along the plate 3. Remains unchanged
J
a
s
p
a
l
S
i
r
Use code "JASPALLIVE" for instant maximum discount on Unacademy Plus subscriptions.](https://image.slidesharecdn.com/fmchapter-11-230929214805-0c560f23/85/FM-chapter-11-pdf-38-320.jpg)