3. Τα θσθιώκαηα ηοσ σποιογηζηή
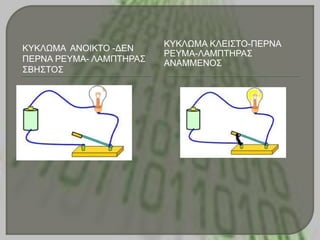
«θαηαιαβαίλοσλ» κόλο δύο θαηαζηάζεης.
Τελ θαηάζηαζε ζηελ οποία δελ περλά ρεύκα
κέζα από ηο θύθιφκα θαη ο ιακπηήρας είλαη
ζβεζηός.
Τελ θαηάζηαζε ζηελ οποία περλά ρεύκα κέζα
από ηο θύθιφκα θαη ο ιακπηήρας είλαη
αλακκέλος.

4. ΚΤΚΛΩΜΑ ΑΝΟΙΚΣΟ -ΓΔΝ
ΠΔΡΝΑ ΡΔΤΜΑ- ΛΑΜΠΣΗΡΑ΢
΢ΒΗ΢ΣΟ΢
ΚΤΚΛΩΜΑ ΚΛΔΙ΢ΣΟ-ΠΔΡΝΑ
ΡΔΤΜΑ-ΛΑΜΠΣΗΡΑ΢
ΑΝΑΜΜΔΝΟ΢

5. Άρα ο σποιογηζηής κπορεί λα τεηρηζηεί κόλο
δύο θαηαζηάζεης, ηελ θαηάζηαζε ζηελ οποία
περλά ρεύκα θαη ηελ θαηάζηαζε ζηελ οποία
δελ περλά ρεύκα.
Οη θαηαζθεσαζηές αληηζηοητούλ:
Τελ αποσζία ρεύκαηος κε ηο κεδέλ «0»
Τελ παροσζία ρεύκαηος κε ηο έλα «1»

6. Άρα έτοσκε έλα ζύζηεκα κε δύο υεθία θαη
γη’ ασηό ολοκάδεηαη δσαδηθό. Τα δσαδηθά υεθία
είλαη ηο 0 θ΄ ηο 1 θαη αληηζηοητούλ ζηης δύο
θαηαζηάζεης ποσ «αληηιακβάλεηαη» ο σποιογηζηής
ο οποίος γη’ ασηό ηο ιόγο
ολοκάδεηαη υεθηαθός.
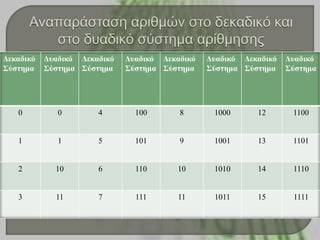
Επεηδή ο σποιογηζηής «θαηαιαβαίλεη» κόλο ηα
δύο ασηά υεθία ( 0 θ΄ 1) γη’ ασηό γηα ηελ
αλαπαράζηαζε ηφλ αρηζκώλ ζηολ σποιογηζηή δελ
τρεζηκοποηούκε ηο δεθαδηθό ζύζηεκα αρίζκεζες
ποσ αποηειείηαη από δέθα υεθία(0,1,2,3,4,5,6,7,8,9)
αιιά ηο δσαδηθό ζύζηεκα αρίζκεζες ποσ έτεη κόλο
δύο υεθία (0,1).

7. Δεθαδηθό
Σύζηεκα
Δσαδηθό
Σύζηεκα
Δεθαδηθό
Σύζηεκα
Δσαδηθό
Σύζηεκα
Δεθαδηθό
Σύζηεκα
Δσαδηθό
Σύζηεκα
Δεθαδηθό
Σύζηεκα
Δσαδηθό
Σύζηεκα
0 0 4 100 8 1000 12 1100
1 1 5 101 9 1001 13 1101
2 10 6 110 10 1010 14 1110
3 11 7 111 11 1011 15 1111

8.  Το δσαδηθό υεθίο ολοκάδεηαη κπηη (bit-binary
digit) παίρλεη δύο ηηκές κεδέλ θαη έλα θαη είλαη
ε βαζηθή κολάδα πιεροθορίας ηφλ
σποιογηζηώλ
 Τα δσαδηθά υεθία τρεζηκοποηούληαη γηα ηελ
παράζηαζε όιφλ ηφλ κορθώλ δεδοκέλφλ ζηολ
σποιογηζηή: αρηζκοί, ταραθηήρες, εηθόλες, ήτοη
θ.ιπ.
 Όηι βλέπουμε ζηον υπολογιζηή ή ακούμε από
αυηόν ή όηι υπολογίδουμε ζε αυηόν είναι
αποηέλεζμα ηων καηάλλελων ζυνδυαζμών
0 και 1