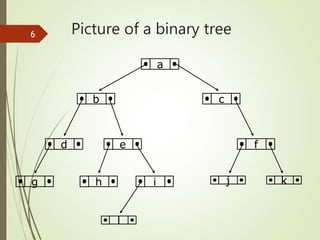
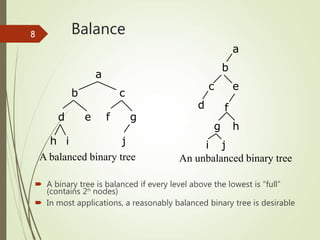
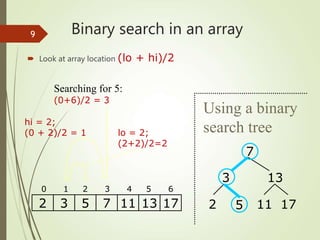
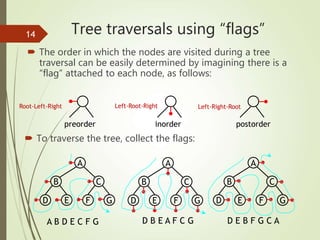
This document discusses binary trees and binary tree traversal. It begins with an overview of the lesson which includes reviewing linear data structures, introducing basic concepts of tree data structures, and discussing binary tree traversal including pre-order, in-order, and post-order traversal. It then defines parts of a binary tree such as nodes, leaves, size, depth, and balance. Finally, it explains the different ways to traverse a binary tree using flags and provides examples of preorder, inorder, and postorder traversal.

1. Week 6
Binary Trees
CC 104 – Data Structures & Algorithms
RIANNEL B. TECSON, MIS
Instructor

2. Flow of the Learning Session
 Short Review of the Previous Lesson
 Basic Concepts on Tree Data Structure
 Lesson Proper & Discussion
 Binary Search Tree Traversal
 Pre-order, In-order, Post-order
 Evaluation
 Guided Practice
 Binary Search Tree Visualization & Animation
 Independent Practice
 Assessment
 Online Quiz
2

3. Recall:
Linear data structures
 Here are some of the data structures we have studied so far:
 Arrays
 Lists
 Queues
 Stacks
 Binary Trees
 These all have the property that their elements can be
adequately displayed in a straight line
 Binary trees are one of the simplest nonlinear data
structures
3

4. Objectives
At the end of the lesson, students should be able to:
 Construct a Binary Search Tree (BST);
 Traverse a BST using Pre-order, In-order, and Post-
order modes
 Use Online Visualization applications to create a
Binary Search Tree and perform Tree Traversals
4

5. Parts of a binary tree
 A binary tree is composed of zero or more nodes
 Each node contains:
 A value (some sort of data item)
 A reference or pointer to a left child (may be null), and
 A reference or pointer to a right child (may be null)
 A binary tree may be empty (contain no nodes)
 If not empty, a binary tree has a root node
 Every node in the binary tree is reachable from the root node by a unique
path
 A node with neither a left child nor a right child is called a leaf
 In some binary trees, only the leaves contain a value
5

6. Picture of a binary tree
6
a
b c
d e
g h i
l
f
j k

7. Size and depth
 The size of a binary tree is the number
of nodes in it
 This tree has size 12
 The depth of a node is its distance
from the root
 a is at depth zero
 e is at depth 2
 The depth of a binary tree is the depth
of its deepest node
 This tree has depth 4
7
a
b c
d e f
g h i j k
l

8. Balance
 A binary tree is balanced if every level above the lowest is “full”
(contains 2n nodes)
 In most applications, a reasonably balanced binary tree is desirable
8
a
b c
d e f g
h i j
A balanced binary tree
a
b
c
d
e
f
g h
i j
An unbalanced binary tree

9. Binary search in an array
 Look at array location (lo + hi)/2
9
2 3 5 7 11 13 17
0 1 2 3 4 5 6
Searching for 5:
(0+6)/2 = 3
hi = 2;
(0 + 2)/2 = 1 lo = 2;
(2+2)/2=2
7
3 13
2 5 11 17
Using a binary
search tree

10. Tree traversals
 A binary tree is defined recursively: it consists of a
root, a left subtree, and a right subtree
 To traverse (or walk) the binary tree is to visit each
node in the binary tree exactly once
 Tree traversals are naturally recursive
 Since a binary tree has three “parts,” there are six
possible ways to traverse the binary tree:
 root, left, right (Preorder)
 left, root, right (Inorder)
 left, right, root (Postorder)
 root, right, left
 right, root, left
 right, left, root
10

11. Tree traversals using “flags”
 The order in which the nodes are visited during a tree
traversal can be easily determined by imagining there is a
“flag” attached to each node, as follows:
 To traverse the tree, collect the flags:
14
preorder inorder postorder
A
B C
D E F G
A
B C
D E F G
A
B C
D E F G
A B D E C F G D B E A F C G D E B F G C A
Root-Left-Right Left-Root-Right Left-Right-Root

12. Practice:
Binary Search Tree Traversal
 https://algorithm-visualizer.org/brute-
force/binary-tree-traversal
 https://yongdanielliang.github.io/animation/web/B
ST.html
15
Binary Search Tree Traversals Applications:

13. Questions?
 Clarifications?
16

14. Assessment:
Binary Search Tree Traversal
 https://docs.google.com/forms/d/e/1FAIpQLSf8RT
BMIkGGapJ4jGxg7z2P-
pE3QaROdxiRHSsrRxm6gcxU2g/viewform?authuse
r=1
17
Answer the problems in Google Form below:

15. Copying a binary tree
 In postorder, the root is visited last
 Here’s a postorder traversal to make a complete copy of a given binary
tree:
public BinaryTree copyTree(BinaryTree bt) {
if (bt == null) return null;
BinaryTree left = copyTree(bt.leftChild);
BinaryTree right = copyTree(bt.rightChild);
return new BinaryTree(bt.value, left, right);
}
18

16. Other traversals
 The other traversals are the reverse of these three standard
ones
 That is, the right subtree is traversed before the left subtree is
traversed
 Reverse preorder: root, right subtree, left subtree
 Reverse inorder: right subtree, root, left subtree
 Reverse postorder: right subtree, left subtree, root
19

17. The End
20