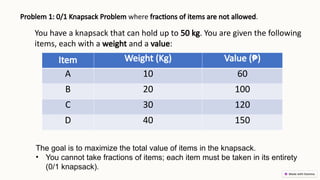
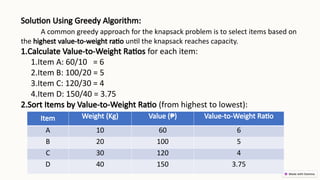
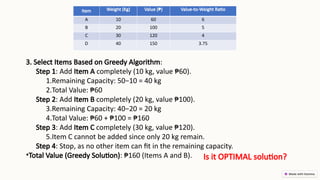
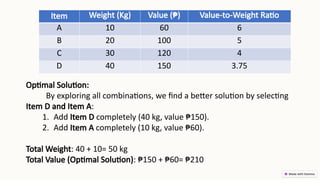
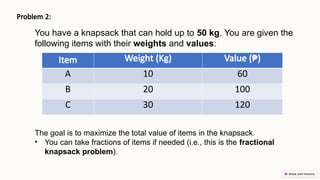
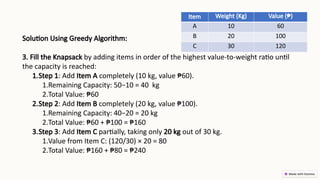
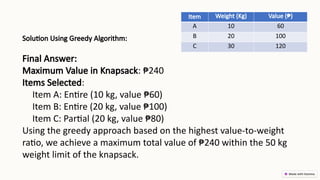
Greedy algorithms make locally optimal choices at each stage in order to find a global optimum, often used for optimization problems due to their simplicity and efficiency. They can lead to quick solutions, but may not guarantee optimal outcomes and can get stuck in local optima. The document discusses the characteristics, advantages, and disadvantages of greedy algorithms, along with examples like the coin change problem, knapsack problem, and Kruskal's algorithm.

1. Greedy Algorithms:
An Introduction
Greedy algorithms are a powerful class of algorithms that make locally
optimal choices at each stage with the goal of finding a global optimum.
They are simple yet effective, and are widely used in solving various
optimization problems.
by Riannel Tecson

2. What are Greedy Algorithms?
1 Stepwise Approach
Greedy algorithms make the
choice that seems best at each
stage, without considering the
long-term consequences.
2 Global Optimality
The goal is to find a global
optimal solution, even though
the algorithm may not
explore all possible options.
3 Efficiency
Greedy algorithms are often efficient and easy to implement,
making them a popular choice for many problems.

3. Characteristics of Greedy Algorithms
Simplicity
Greedy algorithms are
straightforward and easy to
understand, making them a popular
choice for many problems.
Locally Optimal
At each step, the algorithm makes the
choice that seems best at the
moment, without considering the
long-term consequences.
Efficiency
Greedy algorithms are often efficient
and can be implemented in a timely
manner, making them useful for real-
world applications.

4. Advantages and
Disadvantages
Advantages
Greedy algorithms are simple,
efficient, and often produce
good results, making them a
popular choice for many
problems.
Disadvantages
Greedy algorithms may not
always find the global optimal
solution, and can be prone to
getting stuck in local optima.

5. Coin Change Problem
1 Step 1
Define the available coin denominations, such as ₱1, ₱5,
₱10, and ₱20.
2 Step 2
Repeatedly choose the largest coin denomination that is
less than or equal to the remaining amount.
3 Step 3
Continue this process until the entire amount has been
covered, using the minimum number of coins.

6. Sample Problem 1.
Determine the minimum number of coins needed
to make 47 units of currency using denominations
of ₱1, ₱5, ₱10, and ₱20.

7. Sample Problem 1.
Determine the minimum number of coins needed to make 47 units
of currency using denominations of ₱1, ₱5, ₱10, and ₱20.
Solution:
Steps:
₱20: 2 coins (40 used, 7 remaining)
₱5: 1 coin (5 used, 2 remaining)
₱1: 2 coins (2 used, 0 remaining)
Answer: 5 coins (2 of ₱20, 1 of ₱5, 2 of ₱1).

8. Sample Problem 2.
Find the minimum number of coins
required to make ₱33.

9. Sample Problem 2.
Find the minimum number of coins required to
make ₱33.
•Solution:
• Steps:
₱20: 1 coin (20 used, 13 remaining)
₱10: 1 coin (10 used, 3 remaining)
₱1: 3 coins (3 used, 0 remaining)
• Answer: 5 coins (1 of ₱20, 1 of ₱10, 3 of ₱ 1).

10. Optimal solution
• In the coin change problem, an optimal solution means finding the
minimum number of coins needed to make a specified amount, given a
set of denominations.
• This solution may involve a combination of coins that doesn’t always
align with the choices a greedy algorithm would make, particularly
when the greedy approach does not yield the least number of coins.
To define it more precisely:
• Optimal Solution:
The smallest possible number of coins required to make up the
target amount.

11. Optimal solution
For example,
• if you want to make 30 units with denominations of 1, 5, 10, and 20, the greedy
algorithm would choose a 20 and a 10, totaling 2 coins.
• However, an alternative configuration of three 10 coins is also possible.
• Thus, when considering constraints or minimizing specific denominations, an
optimal solution would consider all combinations to ensure the absolute
minimum coin count or a setup that meets all constraints.

12. Sample Problem 3.
Given denominations of coins as 1, 3, and 4, find
the minimum number of coins needed to make 6
units.
How many coins needed to give 6 units using
Greedy algorithm?

13. Sample Problem 3.
Given denominations of coins as 1, 3, and 4, find the
minimum number of coins needed to make 6 units.
How many coins needed to give 6 units using Greedy
algorithm?
Solution Using Greedy Algorithm:
The greedy algorithm selects the largest denomination that doesn’t
exceed the remaining amount at each step.
1. Start with the largest denomination, 4:
1.4: 1 coin (4 used, 2 remaining)
2. Next, use the largest coin that is less than or equal to 2:
1.1: 2 coins (1 + 1 used, 0 remaining)
•Total Coins (Greedy Solution): 3 coins (1 of 4, 2 of 1).

14. Sample Problem 3.
Given denominations of coins as 1, 3, and 4, find the
minimum number of coins needed to make 6 units.
How many coins needed to give 6 units using Greedy
algorithm?
Optimal Solution:
By exploring all possible combinations, we can achieve the
target amount using 2 coins:
1.Use two coins of 3 (3 + 3 = 6).
• Total Coins (Optimal Solution): 2 coins (2 of 3).

15. Knapsack Problem
Define Items
Assign a value and weight to each item that can be placed
in the knapsack.
Maximize Value
Choose the items that maximize the total value while
staying within the weight limit of the knapsack.
Greedy Approach
A greedy algorithm would select the items with the
highest value-to-weight ratio, until the knapsack is full.

16. Problem 1: 0/1 Knapsack Problem where fractions of items are not allowed.
The goal is to maximize the total value of items in the knapsack.
• You cannot take fractions of items; each item must be taken in its entirety
(0/1 knapsack).
You have a knapsack that can hold up to 50 kg. You are given the following
items, each with a weight and a value:
Item Weight (Kg) Value (₱)
A 10 60
B 20 100
C 30 120
D 40 150

17. Solution Using Greedy Algorithm:
A common greedy approach for the knapsack problem is to select items based on
the highest value-to-weight ratio until the knapsack reaches capacity.
1.Calculate Value-to-Weight Ratios for each item:
1.Item A: 60/10 = 6
2.Item B: 100/20 = 5
3.Item C: 120/30 = 4
4.Item D: 150/40 = 3.75
2.Sort Items by Value-to-Weight Ratio (from highest to lowest):
Item Weight (Kg) Value (₱) Value-to-Weight Ratio
A 10 60 6
B 20 100 5
C 30 120 4
D 40 150 3.75

18. 3. Select Items Based on Greedy Algorithm:
Step 1: Add Item A completely (10 kg, value ₱60).
1.Remaining Capacity: 50−10 = 40 kg
2.Total Value: ₱60
Step 2: Add Item B completely (20 kg, value ₱100).
3.Remaining Capacity: 40−20 = 20 kg
4.Total Value: ₱60 + ₱100 = ₱160
Step 3: Add Item C completely (30 kg, value ₱120).
5.Item C cannot be added since only 20 kg remain.
Step 4: Stop, as no other item can fit in the remaining capacity.
•Total Value (Greedy Solution): ₱160 (Items A and B).
Item Weight (Kg) Value (₱) Value-to-Weight Ratio
A 10 60 6
B 20 100 5
C 30 120 4
D 40 150 3.75
Is it OPTIMAL solution?

19. Optimal Solution:
By exploring all combinations, we find a better solution by selecting
Item D and Item A:
1. Add Item D completely (40 kg, value ₱150).
2. Add Item A completely (10 kg, value ₱60).
Total Weight: 40 + 10= 50 kg
Total Value (Optimal Solution): ₱150 + ₱60= ₱210
Item Weight (Kg) Value (₱) Value-to-Weight Ratio
A 10 60 6
B 20 100 5
C 30 120 4
D 40 150 3.75

20. Problem 2:
The goal is to maximize the total value of items in the knapsack.
• You can take fractions of items if needed (i.e., this is the fractional
knapsack problem).
You have a knapsack that can hold up to 50 kg. You are given the
following items with their weights and values:
Item Weight (Kg) Value (₱)
A 10 60
B 20 100
C 30 120

21. Solution Using Greedy Algorithm:
In the fractional knapsack problem, the greedy approach
selects items based on the highest value-to-weight ratio.
1.Calculate Value-to-Weight Ratios for each item:
1. Item A: 60/10 = 6
2. Item B: 100/20 = 5
3. Item C: 120/30 = 4
2.Sort Items by Value-to-Weight Ratio (from highest to lowest):
1.Item A (6)
2.Item B (5)
3.Item C (4)

22. Solution Using Greedy Algorithm:
3. Fill the Knapsack by adding items in order of the highest value-to-weight ratio until
the capacity is reached:
1.Step 1: Add Item A completely (10 kg, value ₱60).
1.Remaining Capacity: 50−10 = 40 kg
2.Total Value: ₱60
2.Step 2: Add Item B completely (20 kg, value ₱100).
1.Remaining Capacity: 40−20 = 20 kg
2.Total Value: ₱60 + ₱100 = ₱160
3.Step 3: Add Item C partially, taking only 20 kg out of 30 kg.
1.Value from Item C: (120/30) × 20 = 80
2.Total Value: ₱160 + ₱80 = ₱240
Item Weight (Kg) Value (₱)
A 10 60
B 20 100
C 30 120

23. Solution Using Greedy Algorithm:
Final Answer:
Maximum Value in Knapsack: ₱240
Items Selected:
Item A: Entire (10 kg, value ₱60)
Item B: Entire (20 kg, value ₱100)
Item C: Partial (20 kg, value ₱80)
Using the greedy approach based on the highest value-to-weight
ratio, we achieve a maximum total value of ₱240 within the 50 kg
weight limit of the knapsack.
Item Weight (Kg) Value (₱)
A 10 60
B 20 100
C 30 120

24. Kruskal's Algorithm
Sort Edges
Sort the edges of the graph in ascending order by weight.
Union-Find
Use a Union-Find data structure to keep track of connected components.
Add Edges
Iteratively add the lightest edge that doesn't create a cycle, until all vertices are
connected.

25. Conclusion and Recap
1 Simplicity
Greedy algorithms are
straightforward and easy to
implement, making them a
popular choice for many
problems.
2 Efficiency
Greedy algorithms are
often efficient and can
produce good results in a
timely manner.
3 Limitations
Greedy algorithms may not always find the global optimal
solution, and can be prone to getting stuck in local optima.