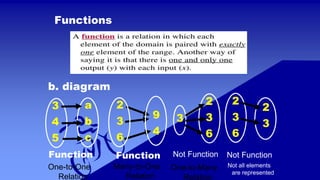
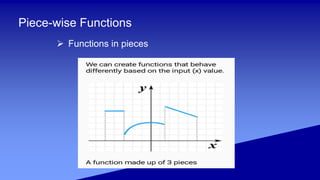
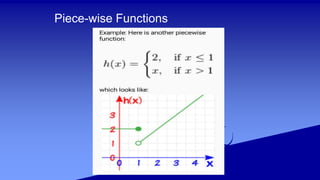
The document covers the definition and characteristics of functions, including one-to-one, many-to-one, and piece-wise functions, and illustrates how these concepts can be applied to real-life situations. It provides examples to determine whether certain sets of ordered pairs and equations represent functions and discusses different types of functions such as polynomial and linear functions. Additionally, it includes problem-solving scenarios involving piece-wise functions to calculate costs based on specific conditions.

1. General Mathematics
Mr. RIANNEL B. TECSON

2. What we are about to learn…
a. Define functions, and piece-wise functions
b. Determine whether a relation is a function
or not;
c. Represent real-life situations using
functions, including piece-wise functions.

3. What will happen to the following if I’m
going to put this into this machine
(factory)?
1.Fish
2.Beef
What about if the machine will produce it
product using f(x) = x + 3
1.4
2.5
3.-2

4. Which of the following machines
represent a FUNCTION?

5. Which of the following machines
represent a FUNCTION?

6. Which of the following machines
represent a FUNCTION?

7. Which of the following machines
represent a FUNCTION?

9. Functions
 Functions relate an input to an
output
Functions in real life:
Output: Score in the test
Input: No. of hours studied

10. Functions
Functions in real life:
 Give another real-life situations
involving functions

11. Functions
Illustration of Functions:
b. mapping or arrow diagram
a. set of ordered pair
c. graphing

12. Functions
a. set of ordered pair
1. {(3,2), (4,0), (5,1), (2,3)} Function
2. {(1,2), (0,3), (1,6), (5,4)}
3. {(3,4), (3,0), (3,1), (3,3)}
4. {(4,2), (3,2), (6,2), (5,2)}
Not Function
Not Function
Function

13. Functions
a. set of ordered pair ( x, y )
x - First element Domain
y - Second Element Range
Independent variable
Dependent variable

14. Functions
b. diagram
3
4
5
Function
One-to-One
Relation
a
b
c
2
3
6
9
4
3
2
3
6
2
3
6
2
3
Function Not Function Not Function
Many-to-One
Relation
One-to-Many
Relation
Not all elements
are represented

15. Functions
c. graphing

16. Functions
c. graphing

17. Determine if the following sets of ordered pairs, table of
values, and equations represent a function.
1.{(-4,2), (0,9), (-4,-8), (4,5), (-1, 10), (11, 15)}
2.{(math, science), (math, English), (math, economics),
(math, history)}
3.f(x) = x2
4.f(x) = /2x + 9/

18. Piece-wise Functions
 Functions in pieces

19. Piece-wise Functions

20. Piece-wise Functions

21. Piece-wise Functions

22. Write a piece-wise function from the given problem.
A Doctor's fee is based on the length of time.
•Up to 6 minutes costs Php 300
•Over 6 to 15 minutes costs Php 500
•Over 15 minutes costs Php 500 plus Php 100 per minute
above 15 minutes

23. A. Determine if the following sets of ordered pairs, table of values,
and equations represents a function.
1.{(5,9), (0,-3), (3,1), (11,-7)}
2.{(apple, banana), (apple, guyabano), (apple, guava), (apple,
pineapple)}
3.f(x) = x4
4.x = y2
5. X 2 6 2 8
f(x) 4 8 9 10

24. B. Problem solving using piecewise function
A merchant sells rice at Php 45.00 a kilo. If however, a buyer
buys more than 150 kilos of rice, the merchant gives a 10%
discount.
1. If x represents the number of kilos of rice purchased,
express the amount to be paid by f(x).
2. How much should be paid for 100 kilos of rice?
3. How much should be paid for 200 kilos of rice?

25. A Function f is a correspondence between two sets, the
domain and the range, such that for each value in the
domain, there corresponds exactly one value in the
range.
A Piece-wise function is a function which consists of two
or more functions in a specified domain.

26. Types of Functions
1.Polynomial function
2.Constant function
3.Linear function
4.Quadratic function
5.Cubic function

27. Determine if the following sets of ordered
pairs, table of values, and equations represent
a function.
1. {(-4,2), (0,9), (-4,-8), (4,5), (-1, 10), (11, 15)}
2.{(math, science), (math, English), (math,
economics), (math, history)}
3.f(x) = x2
4.f(x) = /2x + 9/

28. Functions
Answer Me:
Is this relation a function?
1. {(1,3),(2,3),(3,3)}
2. {(2,3),(2,3),(4,3)}
3. {(-3,3),(-2,3),(-
5,3)}
4. {(1,4),(2,4),(3,4)}
Yes
No
Yes
Yes

29. Functions
Answer Me:
Is this relation a function?
Yes
No

30. Functions
Answer Me:
Is this graph a function?
Yes
No

31. Functions
Answer Me:
Is this graph a function?

32. Functions
Answer Me:
Find the value:
1. f(x) = 3x2 - 4x + 9
x = 0, x = -2
2. h(x) = 4x3 - 6x - 12
3. g(x) = 5x + 4
4. f(x) = x2 + 5x
f(0) = 9 f(-2) = 29
h(0) = -12
f(0) = 0
g(0) = 4
h(-2) = 32
g(-2) = -6
f(-2) = -6

33. Activity:
• Function: (Oh
Yes!)
• Not Function: (Oh
No!)
1. {(-2,3),(2,3),(-3,3)}
2. {(3,3),(2,2),(4,4)}
3. {(1,8),(1,5),(1,3)}
4. {(7,3),(8,3),(5,3)}
Oh Yes!
Oh Yes!
Oh No!
Oh Yes!

34. Activity:
• Function: (Oh Yes!) • Not Function: (Oh No!)
Oh Yes!
Oh No!
Oh Yes!
Oh No!

35. Activity:
• Function: (Oh Yes!) • Not Function: (Oh
No!)
Oh Yes! Oh No! Oh Yes!
Oh No!

36. Activity:
• Function: (Oh Yes!) • Not Function: (Oh No!)
Oh Yes!
Oh No!
Oh Yes!
Oh No!

37. Functions
Assessment:
A. Which of the following are functions
1. {(4,3),(-4,3),(3,3)}
2. {(2,5),(4,4),(2,3)}
Function
Not Function
Not Function
Function
3. 4
.