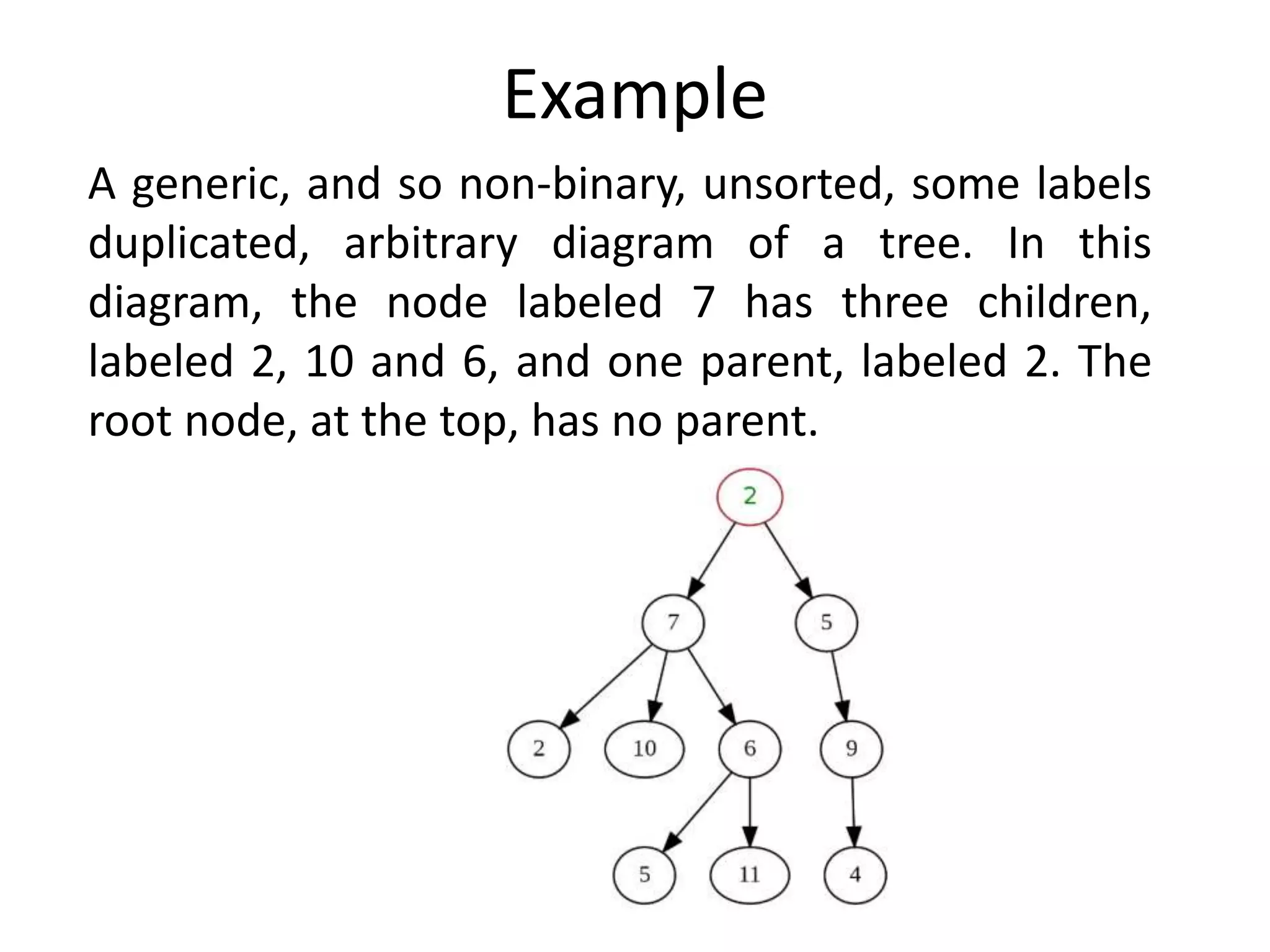
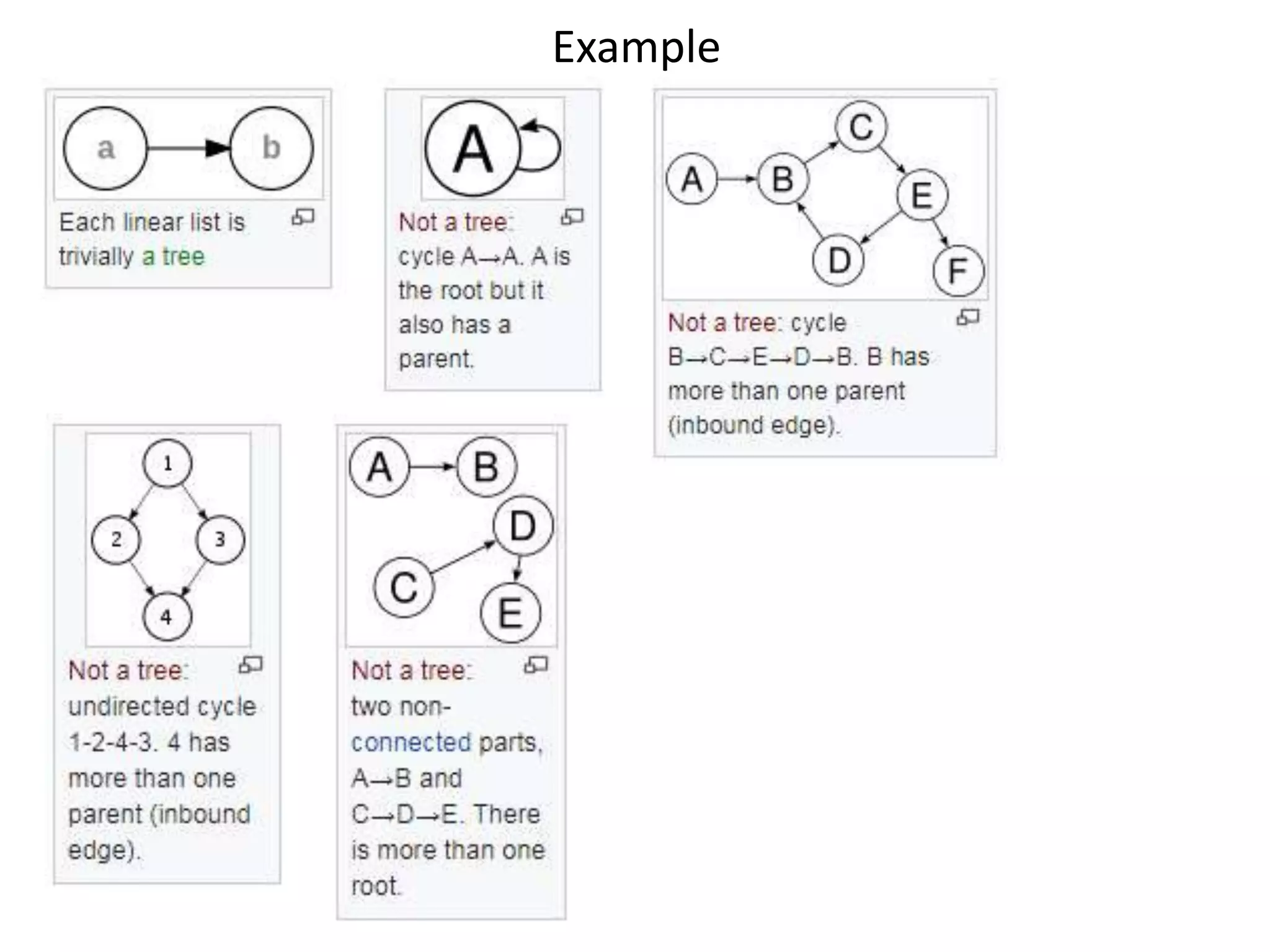
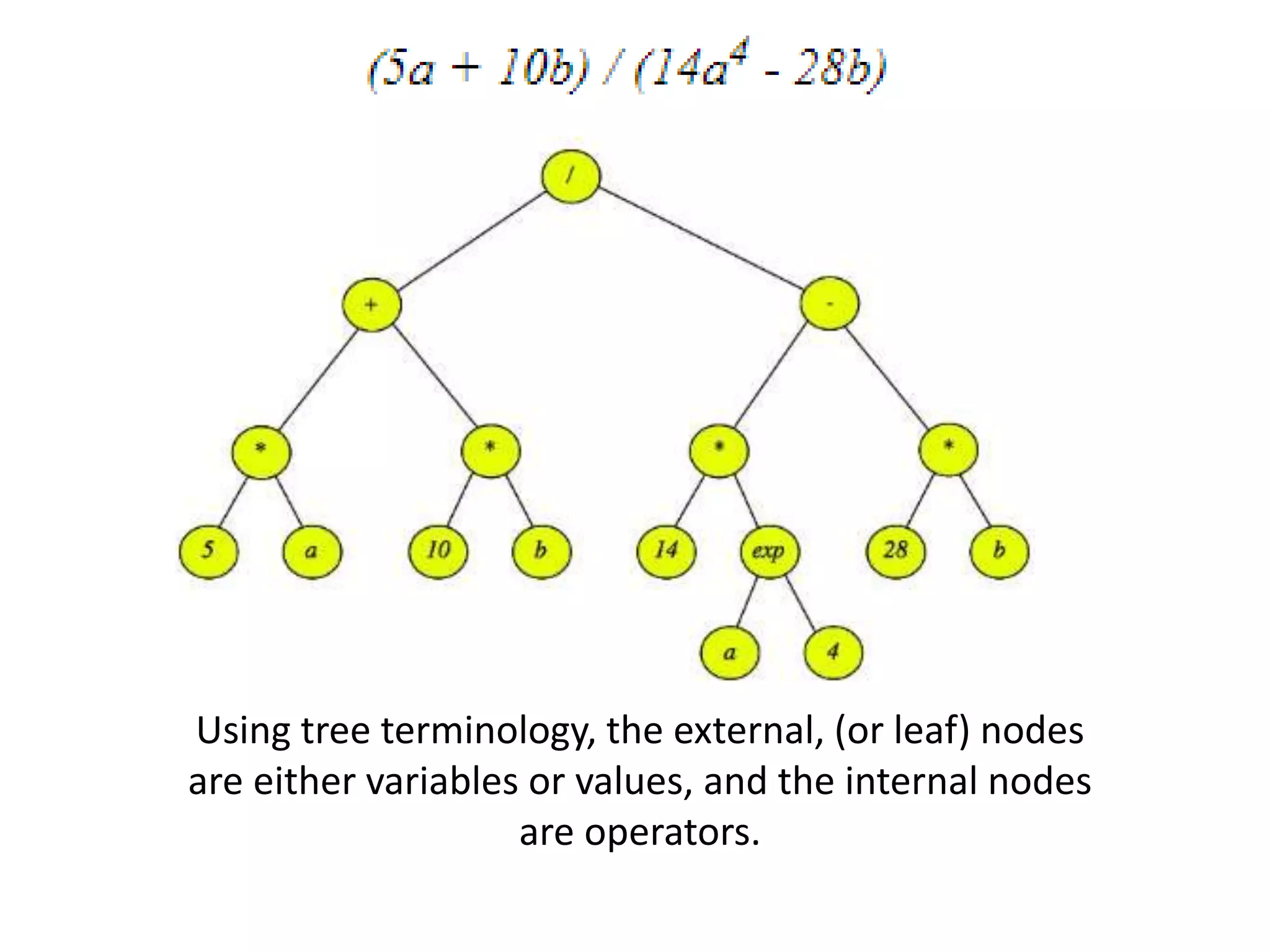
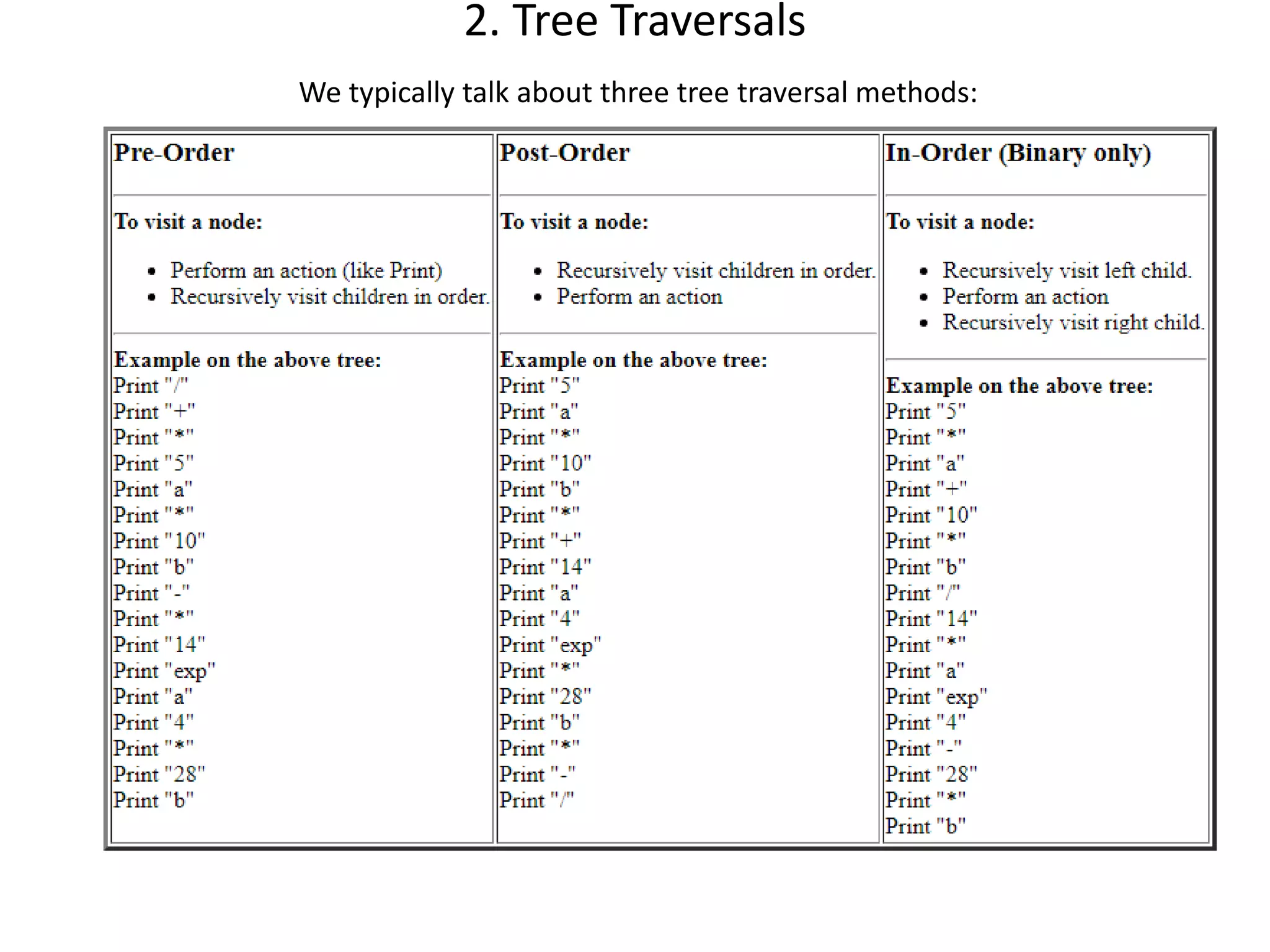
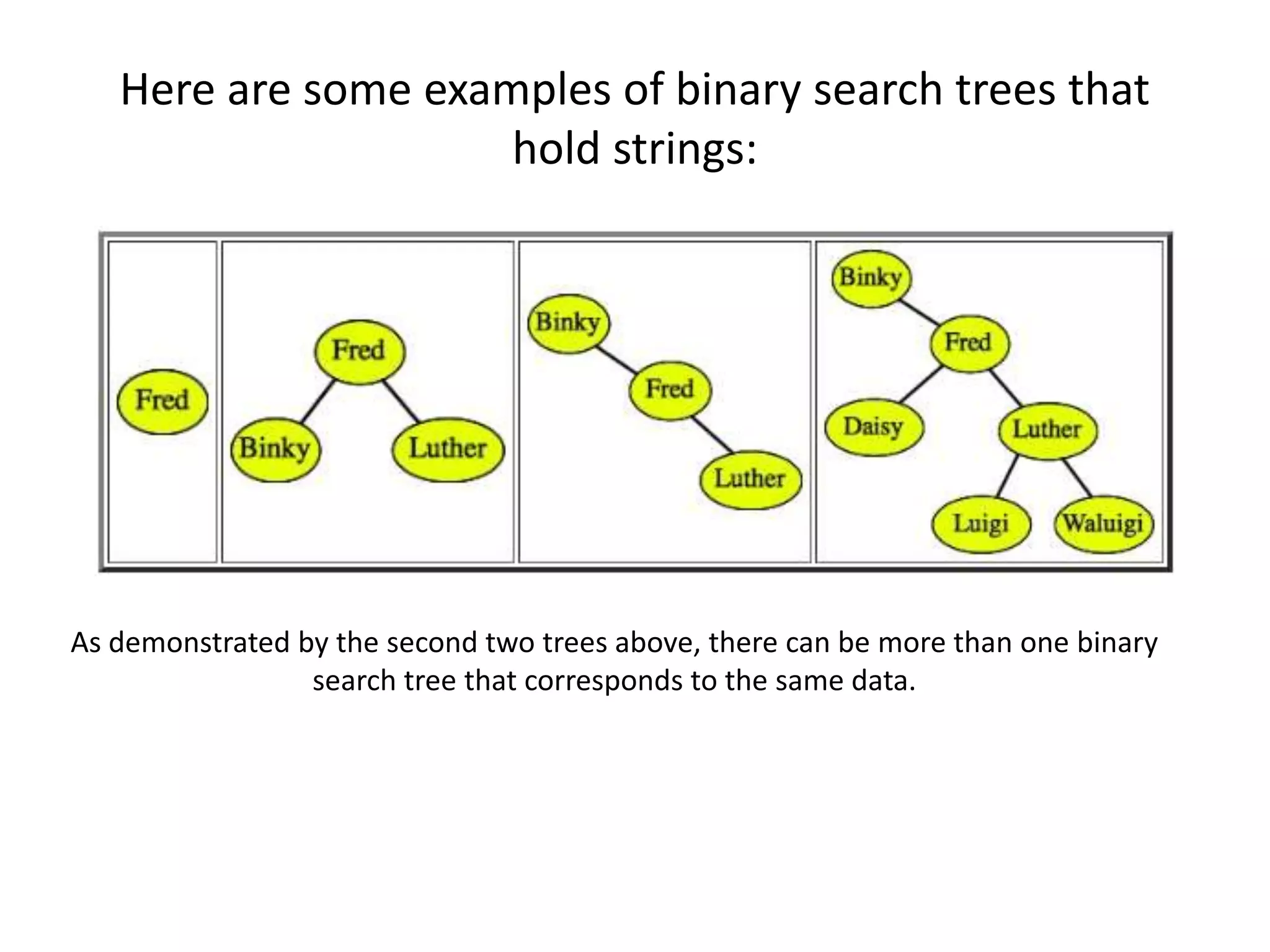
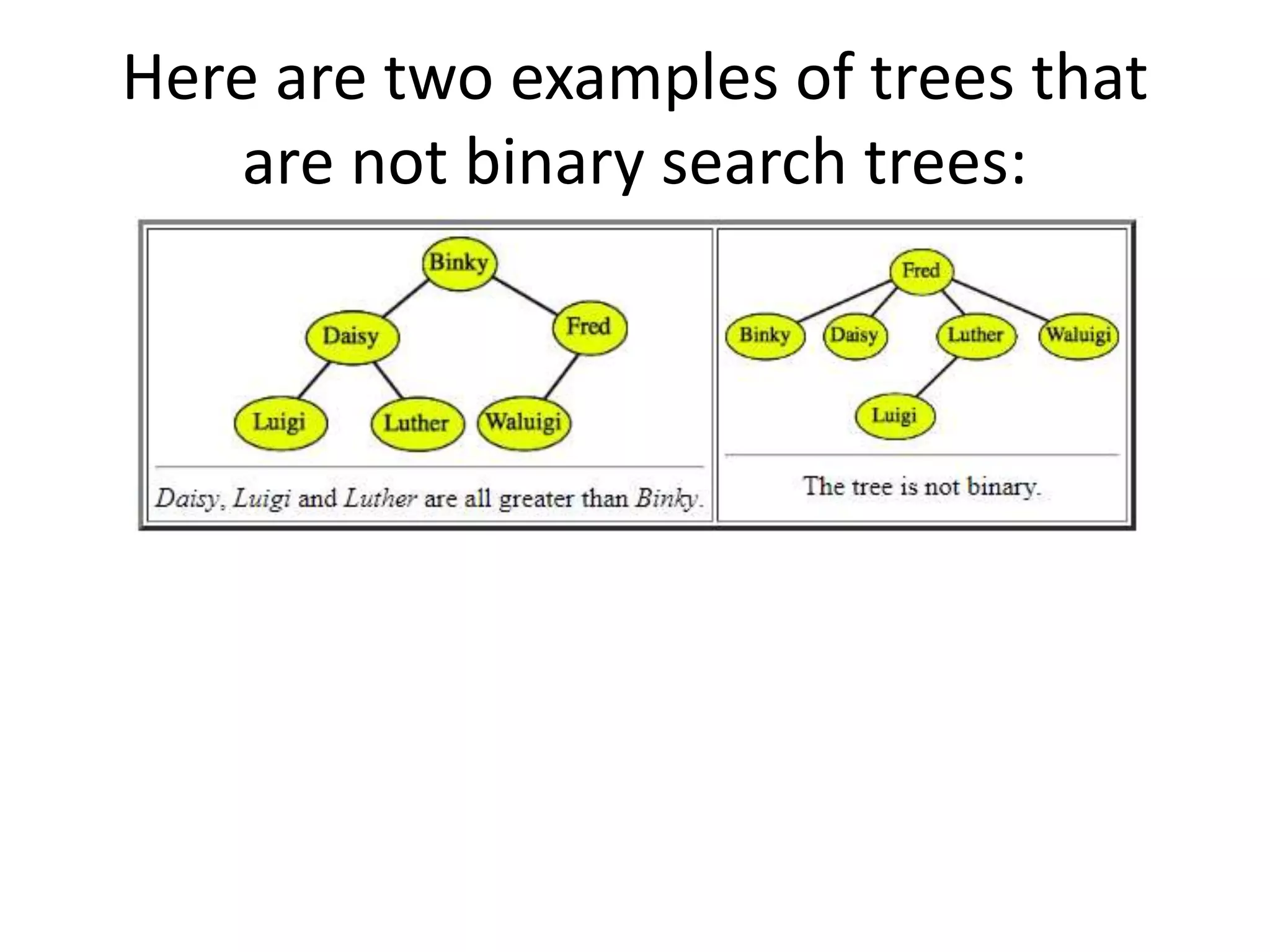
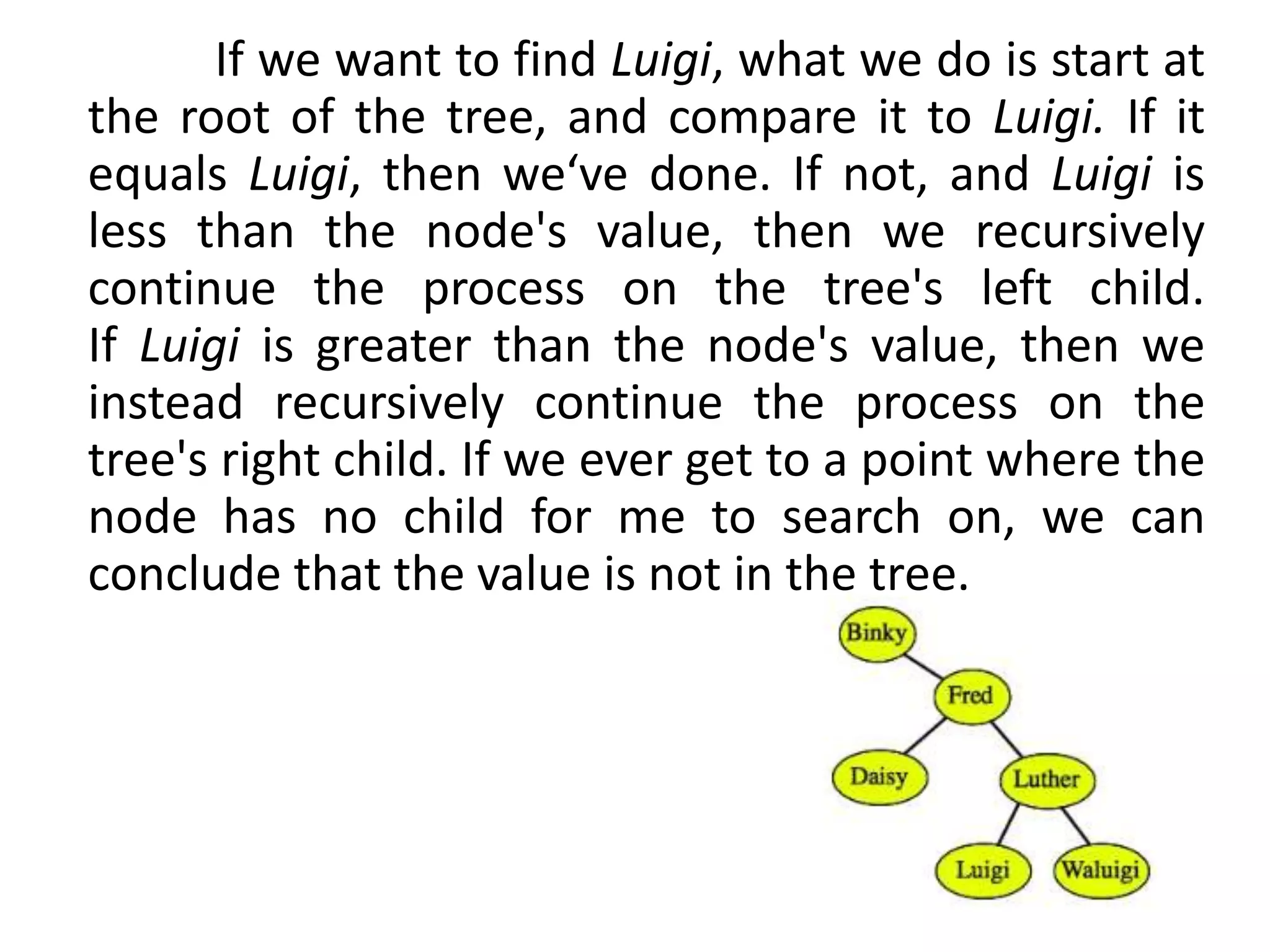
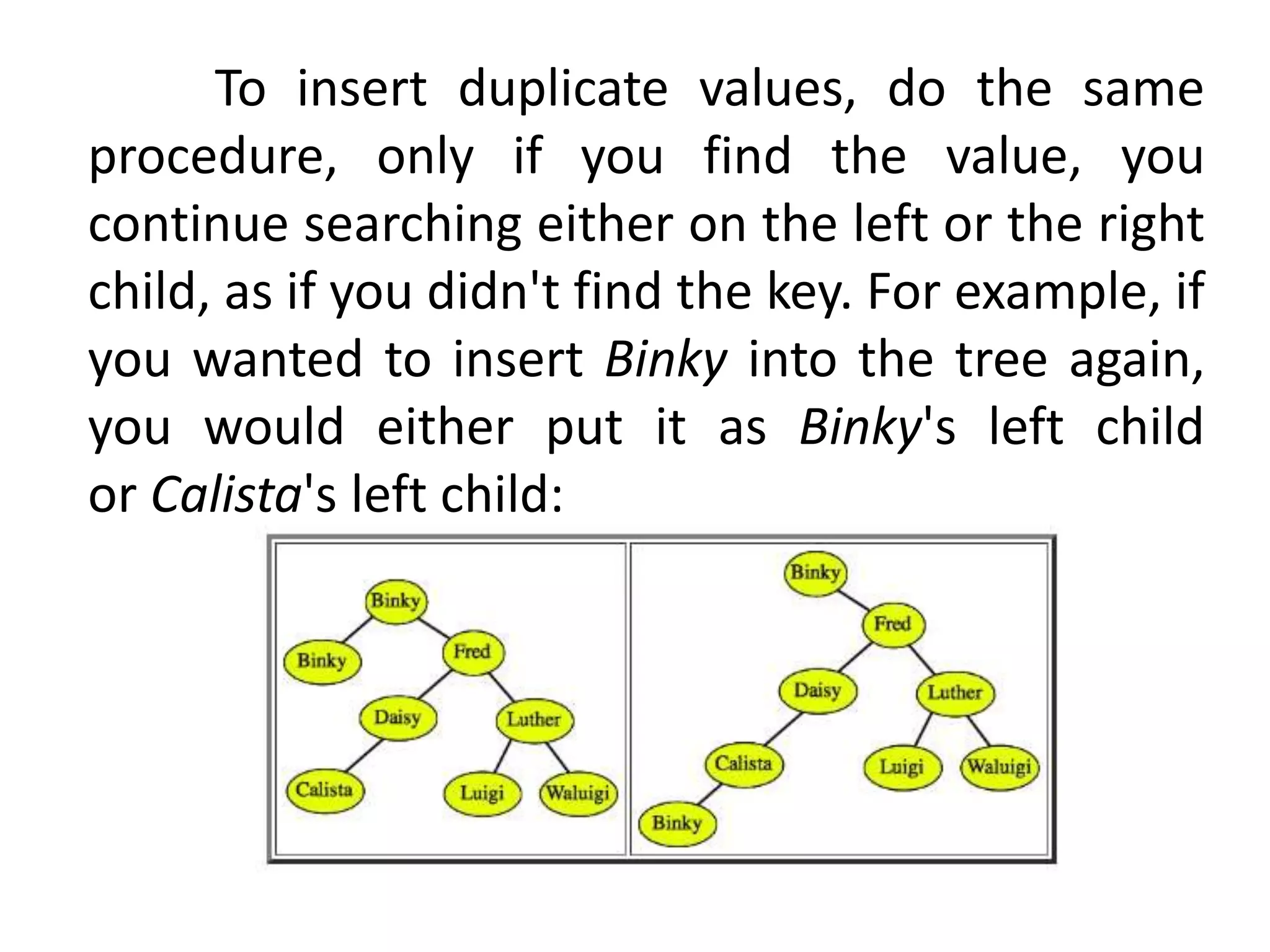
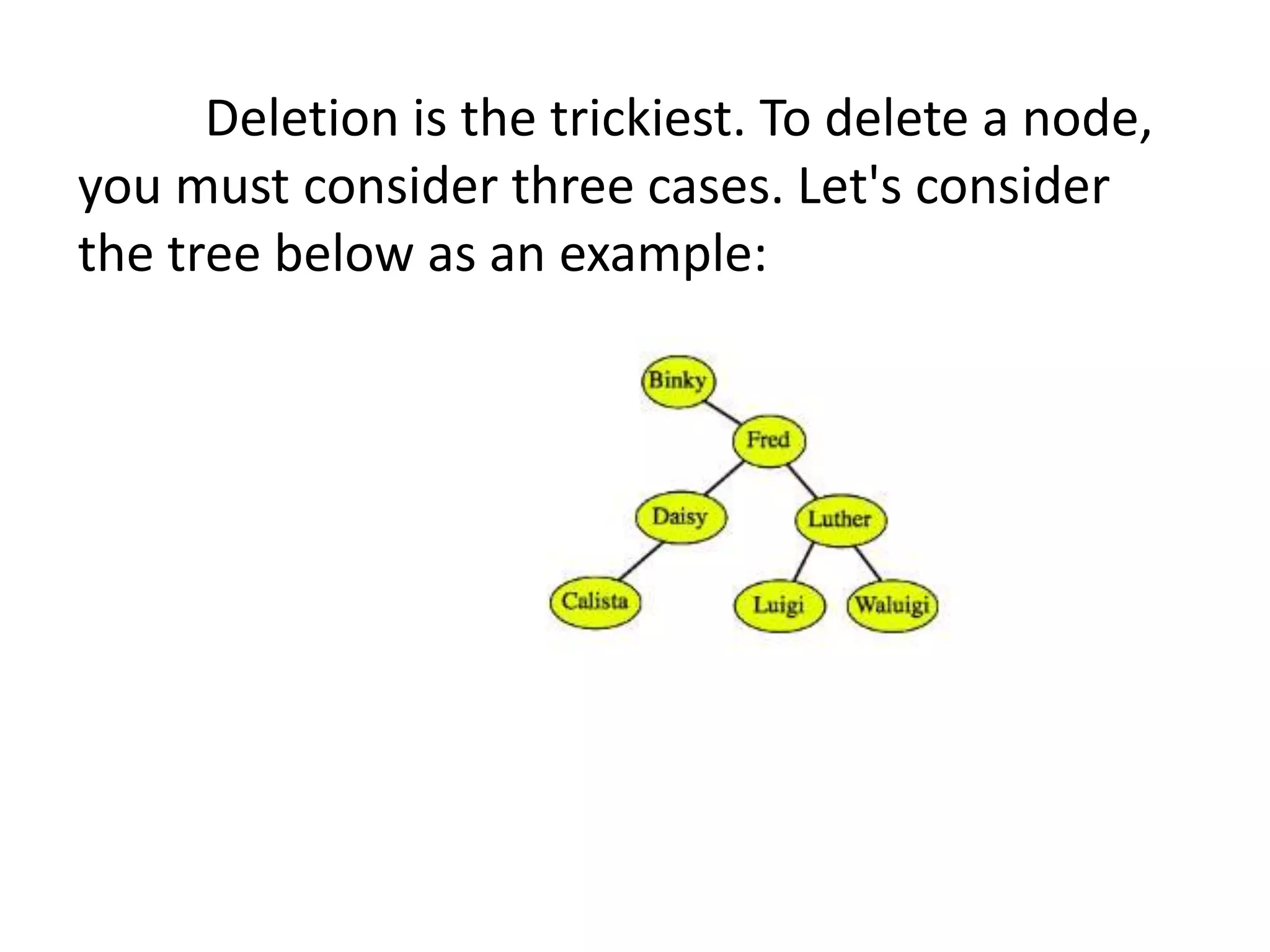
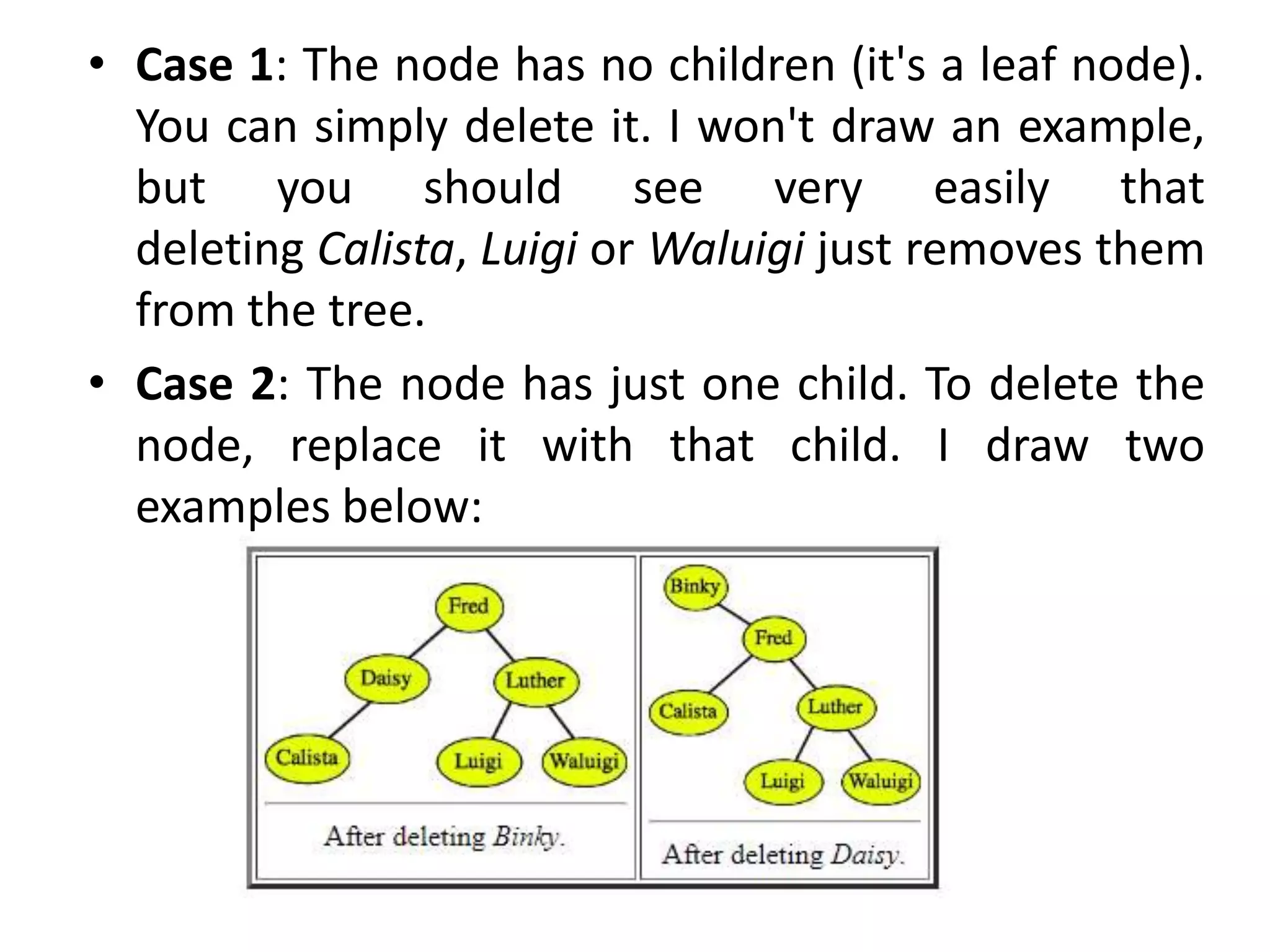
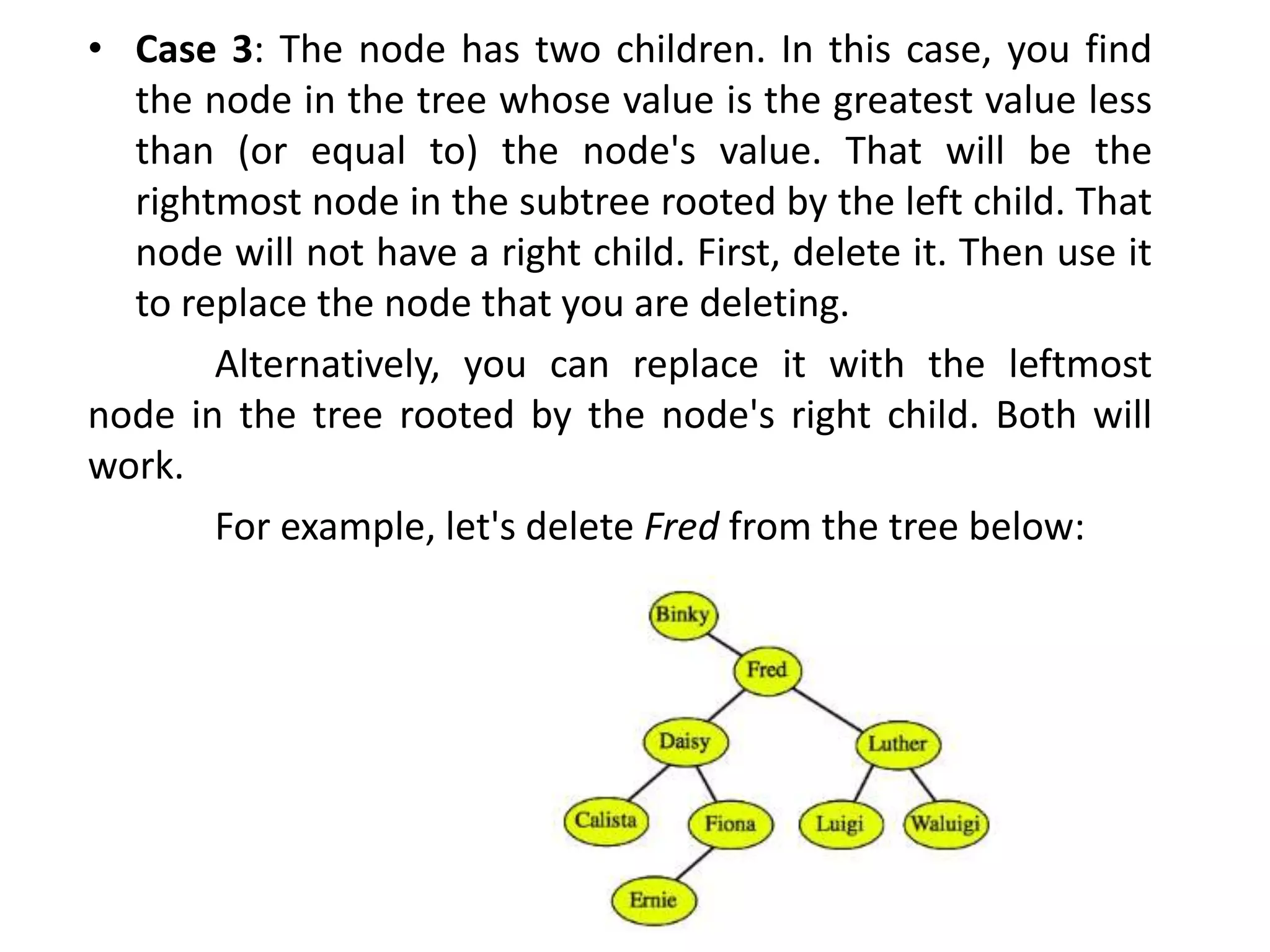
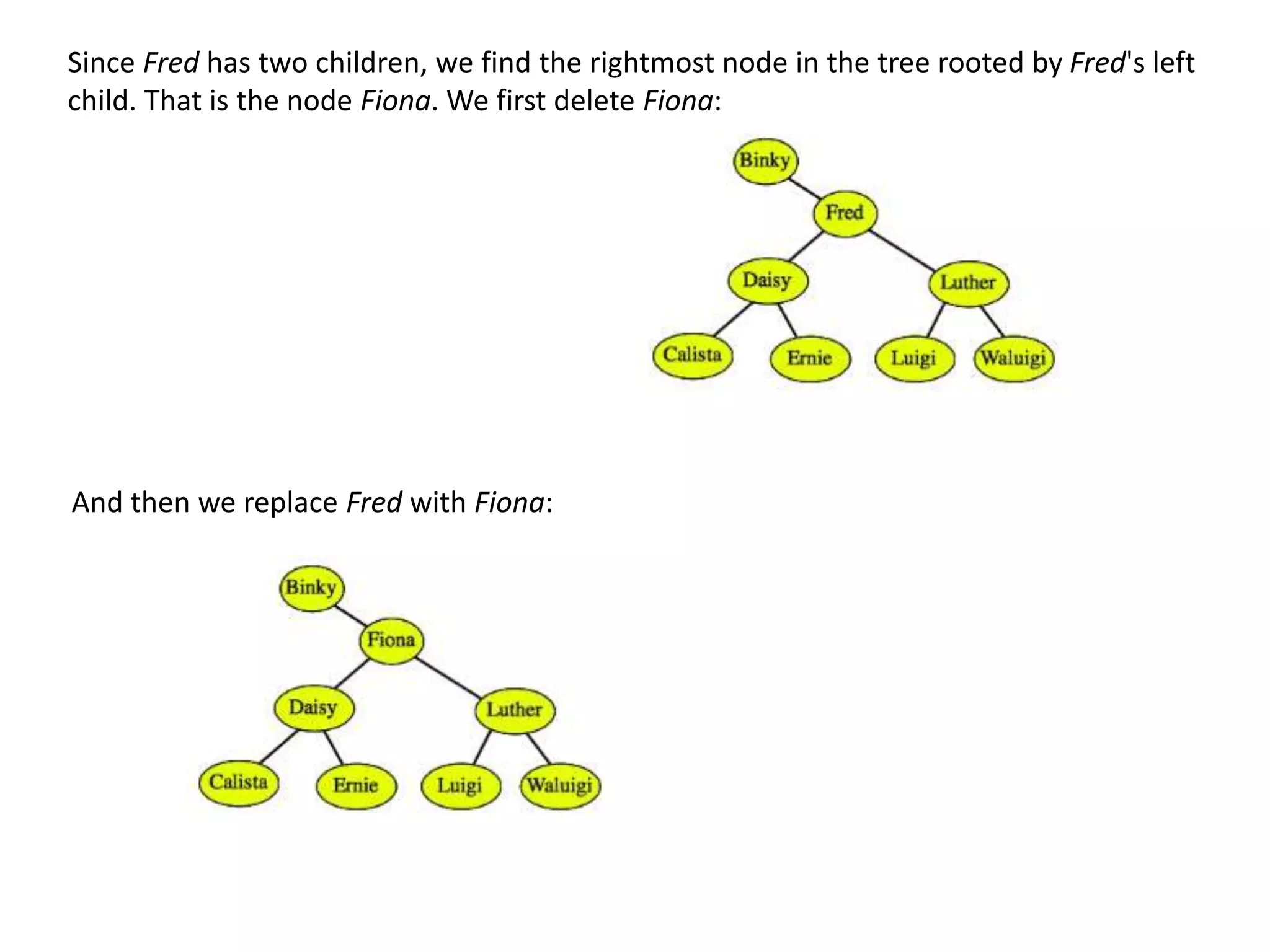
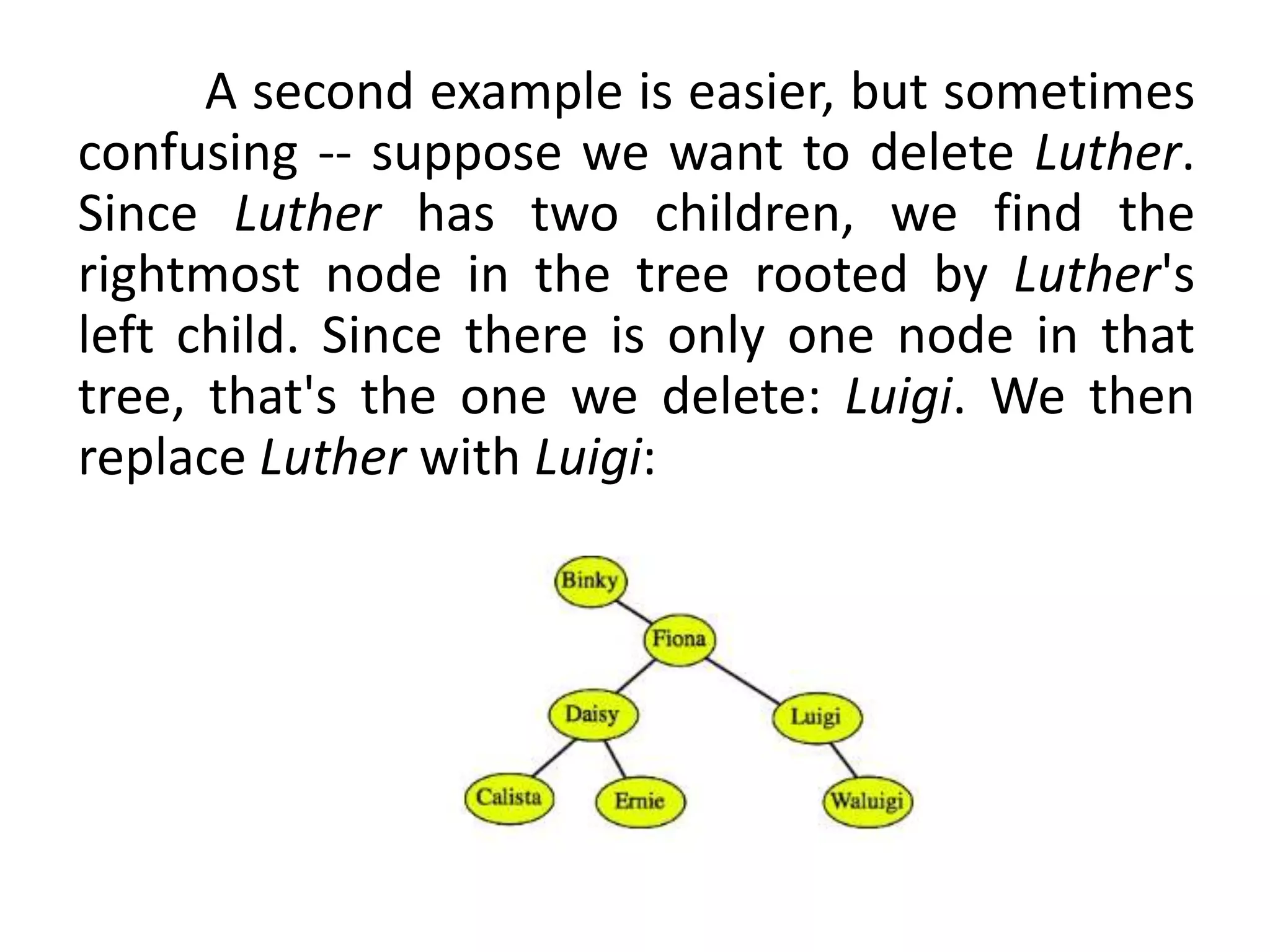
This document discusses tree data structures and binary search trees. It begins with definitions of trees and their components like nodes, edges, and root/child relationships. It then covers tree traversals like preorder, inorder and postorder. Next, it defines binary search trees and their properties for storing and retrieving data efficiently. It provides examples of inserting, searching for, and deleting nodes from binary search trees. Searching and insertion are straightforward, while deletion has three cases depending on the number of child nodes.

1. Tree data structure

2. Plan
1. Definition of the tree
2. Tree Traversals
3. Binary Search Tree Operations: Find, Insert,
Delete

3. 1. Tree
In computer science, a tree is a widely
used abstract data type (ADT) that simulates a
hierarchical tree structure, with a root value and
subtrees of children with a parent node,
represented as a set of linked nodes.
A tree data structure can be defined recursively as a
collection of nodes (starting at a root node), where
each node is a data structure consisting of a value,
together with a list of references to nodes (the
"children"), with the constraints that no reference is
duplicated, and none points to the root.

4. Tree
Alternatively, a tree can be defined abstractly as a
whole (globally) as an ordered tree, with a value assigned
to each node. Both these perspectives are useful: while a
tree can be analyzed mathematically as a whole, when
actually represented as a data structure it is usually
represented and worked with separately by node (rather
than as a set of nodes and an adjacency list of edges
between nodes, as one may represent a digraph, for
instance). For example, looking at a tree as a whole, one
can talk about "the parent node" of a given node, but in
general as a data structure a given node only contains the
list of its children, but does not contain a reference to its
parent (if any).

5. Example
A generic, and so non-binary, unsorted, some labels
duplicated, arbitrary diagram of a tree. In this
diagram, the node labeled 7 has three children,
labeled 2, 10 and 6, and one parent, labeled 2. The
root node, at the top, has no parent.

6. A tree is a nonlinear data structure,
compared to arrays, linked lists, stacks and
queues which are linear data structures. A tree
can be empty with no nodes or a tree is a
structure consisting of one node called the root
and zero or one or more subtrees.
Preliminary definition

7. Example

8. Mathematical definition
Mathematically, an unordered tree (or
"algebraic tree") can be defined as an algebraic
structure (X,parent) where X is the non-empty
carrier set of nodes and parent is a function
on X which assigns each node x its "parent"
node, parent(x). The structure is subject to the
condition that every non-empty subalgebra must
have the same fixed point. That is, there must be a
unique "root" node r, such that parent(r) = r and for
every node x, some iterative
application parent(parent(...parent(x)...)) equals r.

9. There are several equivalent definitions. As
the closest alternative, one can define
unordered trees
as partial algebras (X, parent) which are
obtained from the total algebras described
above by letting parent(r) be undefined. That is,
the root r is the only node on which
the parent function is not defined and for every
node x, the root is reachable from x in
the directed graph (X, parent).
Mathematical definition

10. A tree is a basic linked data structure that
is richer than a list.
Trees are often a very natural way to
represent hierarchies. For example, the
mathematical expression
is very clearly represented by the following tree:

11. Using tree terminology, the external, (or leaf) nodes
are either variables or values, and the internal nodes
are operators.

12. 2. Tree Traversals
We typically talk about three tree traversal methods:

13. • Example Question: "Which of the above
traversals would allow you to evaluate the
expression of the above tree?"
• Answer: A post-order traversal -- for each
operator in an internal node, you need to first
evaluate each of its children before you can
perform the operation. For example, you need to
evaluate the left subtree of "/" and then the right
subtree before you divide the two answers to get
the final evaluation of the expression.

14. Binary Search Trees
Binary search trees are an exceptionally
important type of tree. As their name implies, they
are binary trees, where each node has a value, a
left child and a right child. The important property
of a binary search tree is the following:
• If a node has a left child, then the left child is the
root of a binary search tree whose maximum
value is less than or equal to the node's value.
• If a node has a right child, then the right child is
the root of a binary search tree whose minimum
value is greater than or equal to the node's value.

15. Here are some examples of binary search trees that
hold strings:
As demonstrated by the second two trees above, there can be more than one binary
search tree that corresponds to the same data.

16. Here are two examples of trees that
are not binary search trees:

17. Binary search trees have nice properties.
For example, you can sort the data by
performing an in-order traversal. You can also
find a piece of data simply by traversing a single
path from the root to the data, or to where the
data would be. For example, in the tree:

18. If we want to find Luigi, what we do is start at
the root of the tree, and compare it to Luigi. If it
equals Luigi, then we‘ve done. If not, and Luigi is
less than the node's value, then we recursively
continue the process on the tree's left child.
If Luigi is greater than the node's value, then we
instead recursively continue the process on the
tree's right child. If we ever get to a point where the
node has no child for me to search on, we can
conclude that the value is not in the tree.

19. Continuing the example of finding Luigi, we would:
• We start at Binky. Since Luigi is greater
than Binky, we will continue searching on Binky's
right child.
• We are next at Fred. Again, Luigi is greater
than Fred, so we continue searching on Fred's
right child.
• Now we are at Luther. Luigi is less than Luther, so
we continue searching on Luther's left child.
• We have found Luigi.

20. Similarly, suppose we try to find Calista:
• We start at Binky. Since Calista is greater than Binky,
we'll continue searching on Binky's right child.
• We are next at Fred. Calista is less than Fred, so we
continue searching on Fred's left child.
• Now we are at Daisy. Calista is less than Daisy, so we
continue searching on Daisy's left child.
• However, Daisy has no left child. We can conclude
that Calista is not in the search tree.

21. 3. Binary Search Tree Operations: Find, Insert, Delete
We have just described how to find a value
in a binary search tree. Insertion is a pretty simple
matter too. To insert a value s, assume that s is
not int the tree, and find where s should be.
Create the node and put it there. For example,
were we to insert Calista into the above tree, we
try to find the string. We fail at Daisy's left child,
which doesn't exist. Therefore, we create a node
for Calista and insert it as Daisy's left child:

22. To insert duplicate values, do the same
procedure, only if you find the value, you
continue searching either on the left or the right
child, as if you didn't find the key. For example, if
you wanted to insert Binky into the tree again,
you would either put it as Binky's left child
or Calista's left child:

23. Deletion is the trickiest. To delete a node,
you must consider three cases. Let's consider
the tree below as an example:

24. • Case 1: The node has no children (it's a leaf node).
You can simply delete it. I won't draw an example,
but you should see very easily that
deleting Calista, Luigi or Waluigi just removes them
from the tree.
• Case 2: The node has just one child. To delete the
node, replace it with that child. I draw two
examples below:

25. • Case 3: The node has two children. In this case, you find
the node in the tree whose value is the greatest value less
than (or equal to) the node's value. That will be the
rightmost node in the subtree rooted by the left child. That
node will not have a right child. First, delete it. Then use it
to replace the node that you are deleting.
Alternatively, you can replace it with the leftmost
node in the tree rooted by the node's right child. Both will
work.
For example, let's delete Fred from the tree below:

26. Since Fred has two children, we find the rightmost node in the tree rooted by Fred's left
child. That is the node Fiona. We first delete Fiona:
And then we replace Fred with Fiona:

27. A second example is easier, but sometimes
confusing -- suppose we want to delete Luther.
Since Luther has two children, we find the
rightmost node in the tree rooted by Luther's
left child. Since there is only one node in that
tree, that's the one we delete: Luigi. We then
replace Luther with Luigi: