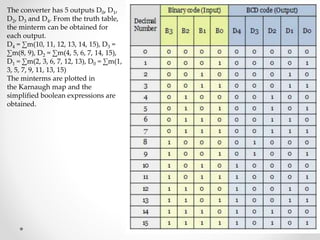
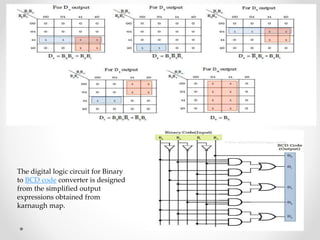
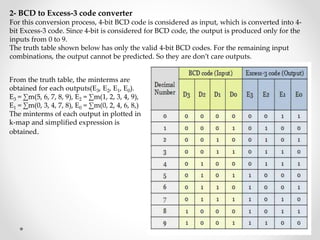
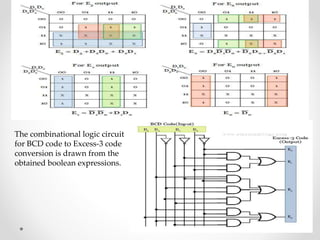
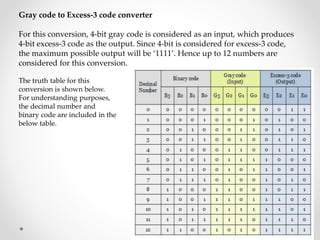
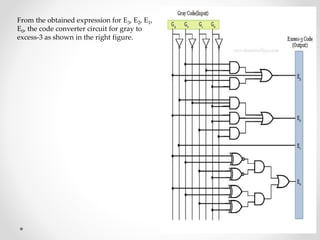
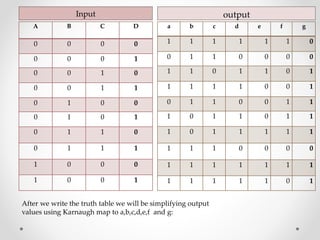
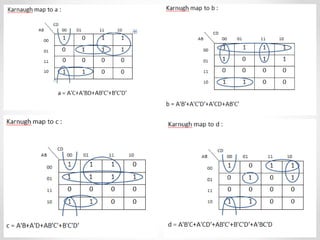
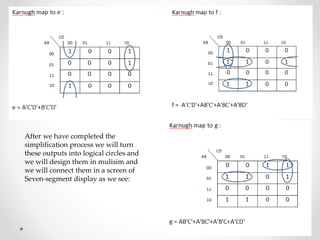
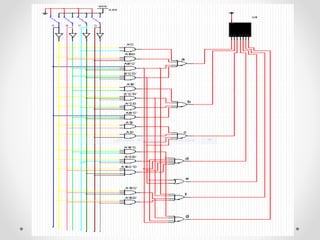
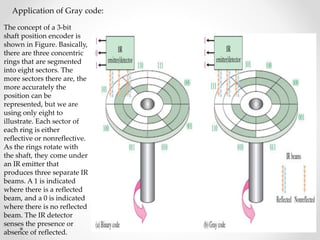
1. The document discusses various types of code conversions including binary to BCD, BCD to excess-3, and gray to excess-3. Circuit designs and truth tables are provided for each conversion. 2. Applications of different codes are covered. BCD is used for 7-segment displays. Gray code is used in shaft encoders. Excess-3 is used for subtraction. 3. The document concludes by designing a BCD to 7-segment display decoder circuit and explaining the application of gray code in shaft encoders.

1. Supervisor:
Dr. Maged Aldhaeebi
Applications of Code conversions
Names: Ahmed Rabea bin Nasser, Ahmed Muthanna

2. Outline:
1- Introduction.
2- Binary to BCD code converter.
3- BCD to Excess-3 code converter.
4- Gray code to Excess-3 code converter.
5- Application of BCD.
6- Application of Gray code.

3. Introduction:
A code converter is a logic circuit that changes data presented in one type of binary code to
another type of binary code. Code conversions are largely used in computers, digital
electronics, microprocessors, etc., to convert one type of binary symbol into another. There
are a variety of binary codes, there are a lot of
symbols such as binary, eight, hexagonal decimal, bi-coded decimal (BCD), Excess-3, gray
code, error correction codes (ECCs) and ASCII code, etc. Binary code is needed for the
machine language and because of the large number of bits.
Code converter is a logical circuit whose inputs are specific bit-shaped symbols representing
the numbers in one code and its outputs are the corresponding expression in a different
code. The chain circuit works this shift by logical gates.

4. Because the outputs depend only on current inputs, this 4-bit binary code to grey code adapter
is a combinational circuit. Also, you can implement other code converters.
The binary symbol of the machine language is needed and because of the large number of bits
required to store the binary code, the eight and six decimal places have been developed which
are easy to write, understand and represent.
We need to draw some code conversion applications.
1. Gray code are used in shaft encoders because The code of successive numbers differs exactly
by one bit from its preceder.
.1
2. Excess- 3 is extensively used for subtraction because every code in XS-3 has its
complement. 1’s complement of the code yields 9’s complement of a number itself.
3. In RAID disks, ECC codes are used for checking the information on the disk at the time of
reading and writing the information and if its mismatch with the information then the
correction is made on the fly.
4. Alphanumeric codes by ASCII standards are widely used as a representation systems to the
character set in computers.
5. BCD to 7 segment LED, the 7 segment LED can be thought of as floors indicator in elevators.
All 7 segement are named as a,b,c,d,e,f,g, which are marked as 0 or 1 for particular 0–9 decimals.
e.g., for 7 a,b,c are turned on because a is for upper segment, b is for upper right, and c is for
bottom right, if these are turned on you would see a 7 on a LED.

5. 6. Code conversions can also be used in code conversion tools or when manually converting
code when working to migrate the old application using outdated technologies to
applications using the latest technology.
A common example is the conversion of applications developed in COBOL or Visual Basic to
applications in C # or Java. Due to the difficulty of preserving old technologies and the
difficulty of finding programmers to maintain them, organizations are moving to newer
technologies.
These are code conversion applications, because of which representation has become simpler
for both programmer and machine because it has become much easier to learn, work,
develop and understand data in machines and how data can be manipulated.
In this section we obtain the code intended of any one type of symbol, use in the conversion
process of the simple code so-called combinational circuits. We will offer three types of
conversion and it is:
1- Binary to BCD code converter
2- BCD to Excess-3 code converter
3- Gray code to Excess-3 code converter

6. 1-Binary to BCD code converter
In BCD code, 0 to 9 numbers represent the equivalent binary numbers. For the numbers
above 10, LSB of a decimal number is represented by its equivalent binary number and MSB
of a decimal number is also represented by their equivalent binary numbers.
For example, the BCD code of 12 is represented as
The following truth table shows the conversion between the binary code input and the BCD
code output. As you see from the table, the 4-bit binary number is converted into 5-bit BCD
code. Decimal code is added in the table to understand the equivalence of Binary and BCD
code.

7. The converter has 5 outputs D0, D1,
D2, D3 and D4. From the truth table,
the minterm can be obtained for
each output.
D4 = ∑m(10, 11, 12, 13, 14, 15), D3 =
∑m(8, 9), D2 = ∑m(4, 5, 6, 7, 14, 15),
D1 = ∑m(2, 3, 6, 7, 12, 13), D0 = ∑m(1,
3, 5, 7, 9, 11, 13, 15)
The minterms are plotted in
the Karnaugh map and the
simplified boolean expressions are
obtained.

8. The digital logic circuit for Binary
to BCD code converter is designed
from the simplified output
expressions obtained from
karnaugh map.

9. 2- BCD to Excess-3 code converter
For this conversion process, 4-bit BCD code is considered as input, which is converted into 4-
bit Excess-3 code. Since 4-bit is considered for BCD code, the output is produced only for the
inputs from 0 to 9.
The truth table shown below has only the valid 4-bit BCD codes. For the remaining input
combinations, the output cannot be predicted. So they are don’t care outputs.
From the truth table, the minterms are
obtained for each outputs(E3, E2, E1, E0).
E3 = ∑m(5, 6, 7, 8, 9), E2 = ∑m(1, 2, 3, 4, 9),
E1 = ∑m(0, 3, 4, 7, 8), E0 = ∑m(0, 2, 4, 6, 8,)
The minterms of each output in plotted in
k-map and simplified expression is
obtained.

10. The combinational logic circuit
for BCD code to Excess-3 code
conversion is drawn from the
obtained boolean expressions.

11. Gray code to Excess-3 code converter
For this conversion, 4-bit gray code is considered as an input, which produces
4-bit excess-3 code as the output. Since 4-bit is considered for excess-3 code,
the maximum possible output will be ‘1111’. Hence up to 12 numbers are
considered for this conversion.
The truth table for this
conversion is shown below.
For understanding purposes,
the decimal number and
binary code are included in the
below table.

12. The minterms of each
output E3, E2, E1, E0 are
plotted in the karnaugh
map and is simplified as
below.
In the k-map shown for E0 output,
although 2 to 3 pairs of cells can be
grouped, all the minterms are
marked as isolated cells to make
simplification easier.
Here you can see the actual boolean
expression obtained from the K-map
for E0 output and you can also see,
how it is simplified to get the
minimal expression

13. From the obtained expression for E3, E2, E1,
E0, the code converter circuit for gray to
excess-3 as shown in the right figure.

14. Application of BCD:
Digital clocks, digital thermometers, digital meters, and other devices with seven-
segment
displays typically use BCD code to simplify the displaying of decimal numbers. BCD is
not as efficient as straight binary for calculations, but it is particularly useful if only
limited
processing is required, such as in a digital thermometer.
But this screen can't understand the inputs that go directly into it, not through a circuit
that converts values into symbols that this screen understands, which is called BCD To
Segment Decoder, It comes in a ready IC format but we will detail this IC from the inside
and the circles it contains from the truth table and karnaugh map and the last we
implement this to logic circuit.
The shape in the right is what we're going to use in the
expression and it's divided into seven pieces which is a,
b, c, d, e, f, g which is going to be the output in the truth
table and for the input it's going to be a value that we're
entering because of course we're going to use Decoder 3
To 8 bit.
a
f
g
e c
d
b

15. Input output
g
f
e
d
c
b
a
0
1
1
1
1
1
1
0
0
0
0
1
1
0
1
0
1
1
0
1
1
1
0
0
1
1
1
1
1
1
0
0
1
1
0
1
1
0
1
1
0
1
1
1
1
1
1
0
1
0
0
0
0
1
1
1
1
1
1
1
1
1
1
1
0
1
1
1
1
1
D
C
B
A
0
0
0
0
1
0
0
0
0
1
0
0
1
1
0
0
0
0
1
0
1
0
1
0
0
1
1
0
1
1
1
0
0
0
0
1
1
0
0
1
After we write the truth table we will be simplifying output
values using Karnaugh map to a,b,c,d,e,f and g:

17. After we have completed the
simplification process we will turn
these outputs into logical circles and
we will design them in mulisim and
we will connect them in a screen of
Seven-segment display as we see:

19. The concept of a 3-bit
shaft position encoder is
shown in Figure. Basically,
there are three concentric
rings that are segmented
into eight sectors. The
more sectors there are, the
more accurately the
position can be
represented, but we are
using only eight to
illustrate. Each sector of
each ring is either
reflective or nonreflective.
As the rings rotate with
the shaft, they come under
an IR emitter that
produces three separate IR
beams. A 1 is indicated
where there is a reflected
beam, and a 0 is indicated
where there is no reflected
beam. The IR detector
senses the presence or
absence of reflected.
Application of Gray code:

20. Summery :
We have known the applications of code converter, its types and its importance in
our real life. We have also designed a circuit of BCD to Seven-segment Decoder and
explained the application of the gray code. In conclusion, we hope that the search
has been admired and that we have succeeded in the explanation.
My colleague Ahmed Muthanna and I sincerely thank you.
References:
1- https://www.electrically4u.com/code-converter-types-truth-table-and-logic-
circuits/
2- https://answer-to-all.com/object/what-are-the-applications-of-code-converters/
3- https://www.quora.com/What-is-the-necessity-of-code-conversions
4- Floyd Digital Fundamentals