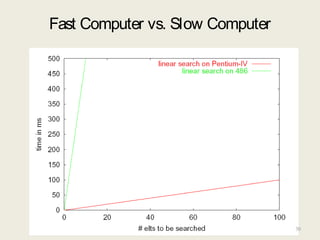
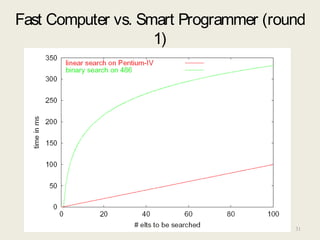
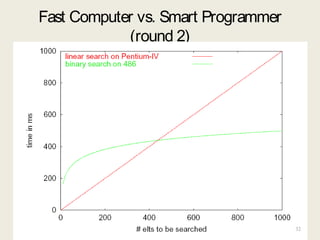
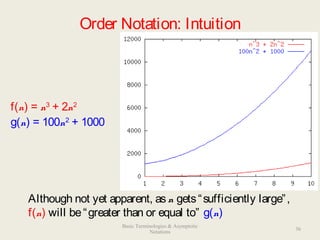
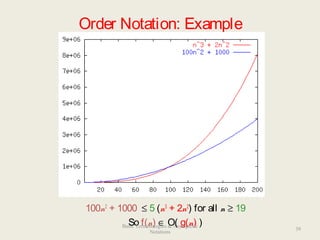
This document discusses data structures and asymptotic analysis. It begins by defining key terminology related to data structures, such as abstract data types, algorithms, and implementations. It then covers asymptotic notations like Big-O, describing how they are used to analyze algorithms independently of implementation details. Examples are given of analyzing the runtime of linear search and binary search, showing that binary search has better asymptotic performance of O(log n) compared to linear search's O(n).














![Program Correctnessby Induction
• Basis Step:
sum(v,0) = 0.
• Inductive Hypothesis (n=k):
Assumesum(v,k) correctly returnssum of first k
elementsof v, i.e. v[0]+v[1]+…+v[k-1]+v[k]
• Inductive Step (n=k+1):
sum(v,n) returns
v[k]+sum(v,k-1)= (by inductive hyp.)
v[k]+(v[0]+v[1]+…+v[k-1])=
v[0]+v[1]+…+v[k-1]+v[k] 15](https://image.slidesharecdn.com/basicterminologiesasymptoticnotations-150624091215-lva1-app6891/85/Basic-terminologies-asymptotic-notations-15-320.jpg)







![Exercise- Searching
bool ArrayFind( int array[], int n, int key){
// Insert your algorithm here
2 3 5 16 37 50 73 75 126
What algo rithm wo uld yo u
cho o se to implement this
co de snippet?
23](https://image.slidesharecdn.com/basicterminologiesasymptoticnotations-150624091215-lva1-app6891/85/Basic-terminologies-asymptotic-notations-23-320.jpg)

![Linear Search Analysis
bool LinearArrayFind(int array[],
int n,
int key ) {
for( int i = 0; i < n; i++ ) {
if( array[i] == key )
// Found it!
return true;
}
return false;
}
Best Case:
Worst Case:
25](https://image.slidesharecdn.com/basicterminologiesasymptoticnotations-150624091215-lva1-app6891/85/Basic-terminologies-asymptotic-notations-25-320.jpg)
![Binary Search Analysis
bool BinArrayFind( int array[], int low,
int high, int key ) {
// Thesubarray isempty
if( low > high ) return false;
// Search thissubarray recursively
int mid = (high + low) / 2;
if( key == array[mid] ) {
return true;
} elseif( key < array[mid] ) {
return BinArrayFind( array, low,
mid-1, key );
} else{
return BinArrayFind( array, mid+1,
high, key );
Best case:
Worst case:
26](https://image.slidesharecdn.com/basicterminologiesasymptoticnotations-150624091215-lva1-app6891/85/Basic-terminologies-asymptotic-notations-26-320.jpg)


![Linear Search vsBinary Search
Linear Search Binary Search
Best Case 4 at [0] 4 at [middle]
Worst Case 3n+2 4 log n + 4
So … which algo rithm is better?
What tradeo ffs can yo u make?
29](https://image.slidesharecdn.com/basicterminologiesasymptoticnotations-150624091215-lva1-app6891/85/Basic-terminologies-asymptotic-notations-29-320.jpg)