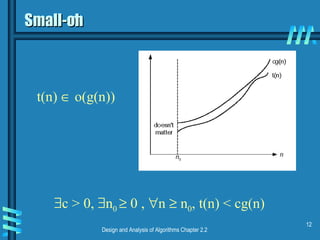
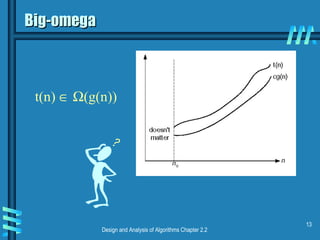
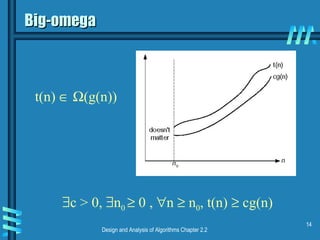
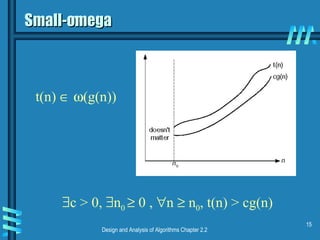
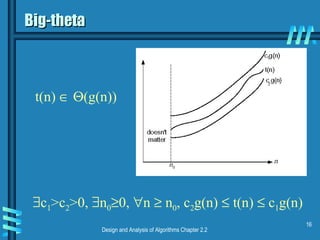
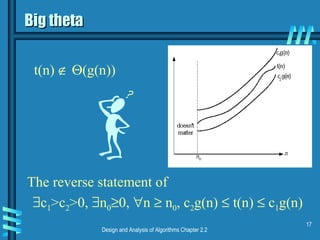
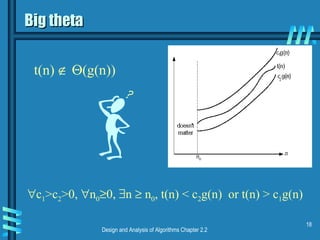
This document discusses key concepts in data structures and asymptotic analysis. It defines common terminology like abstract data type, algorithm, and data structure. It also explains asymptotic notations like Big-O, Big-Omega, and Big-Theta that are used to analyze the time complexity of algorithms. Specifically, it discusses how to establish the rate of growth of an algorithm's time complexity by using definitions, limits, and L'Hopital's rule to compare functions.

1. 1
Basic Terminologies &AsymptoticBasic Terminologies &Asymptotic
NotationsNotations
DataStructuresDataStructures

2. 2
Abstract Data Type (ADT)Abstract Data Type (ADT)
• Mathematical description of an object withMathematical description of an object with
set of operations on the object. Usefulset of operations on the object. Useful
building block.building block.
AlgorithmAlgorithm
• A high level, language independent,A high level, language independent,
description of a step-by-step processdescription of a step-by-step process
Data structureData structure
• A specific family of algorithms forA specific family of algorithms for
implementing an abstract data type.implementing an abstract data type.
Implementation of data structureImplementation of data structure
• A specific implementation in a specificA specific implementation in a specific
languagelanguage
TerminologyTerminology

3. 3
TerminologyTerminology
DataData
Data refers to value orset of values.Data refers to value orset of values.
e.g.Marks obtained by the students.e.g.Marks obtained by the students.
Data typeData type
data type is a classification identifying one of variousdata type is a classification identifying one of various
typestypes
of data, such as floating-point, integer, or Boolean,of data, such as floating-point, integer, or Boolean,
thatthat
determines the possible values for that type; thedetermines the possible values for that type; the
operationsoperations
that can be done on values of that type; and the waythat can be done on values of that type; and the way

4. 4
TerminologyTerminology
Primitive data type:Primitive data type:
These are basic data types that are provided by theThese are basic data types that are provided by the
programming language with built-in support. Theseprogramming language with built-in support. These
datadata
types are native to the language. This data type istypes are native to the language. This data type is
supported by machine directlysupported by machine directly
VariableVariable
Variable is a symbolic name given to someVariable is a symbolic name given to some
known orknown or
unknown quantity orinformation, forthe purposeunknown quantity orinformation, forthe purpose

5. 5
RecordRecord
Collection of related data items is known as record.Collection of related data items is known as record.
TheThe
elements of records are usually Called fields orelements of records are usually Called fields or
members .members .
Records are distinguished from arrays by the factRecords are distinguished from arrays by the fact
thatthat
theirnumberof fields is typically fixed, each field hastheirnumberof fields is typically fixed, each field has
aa
name, and that each field may have a different type.name, and that each field may have a different type.
ProgramProgram
A sequence of instructions that a computercanA sequence of instructions that a computercan
TerminologyTerminology

6. 6
AA stack is anstack is an abstractdatatypeabstractdatatype supporting push, popsupporting push, pop
and isEmpty operationsand isEmpty operations
A stackA stack datastructuredatastructure could use an array, a linkedcould use an array, a linked
list, oranything that can hold datalist, oranything that can hold data
One stackOne stack implementationimplementation is java.util.Stack; anotheris java.util.Stack; another
is java.util.LinkedListis java.util.LinkedList
Terminology examplesTerminology examples

7. 7
AbstractAbstract
PseudocodePseudocode
AlgorithmAlgorithm
• A sequence of high-A sequence of high-
level, languagelevel, language
independentindependent
operations, which mayoperations, which may
act upon an abstractedact upon an abstracted
view of data.view of data.
Abstract Data Type (ADT)Abstract Data Type (ADT)
• A mathematicalA mathematical
description of an objectdescription of an object
and the set ofand the set of
operations on theoperations on the
AbstractAbstract
PseudocodePseudocode
AlgorithmAlgorithm
• A sequence of high-A sequence of high-
level, languagelevel, language
independentindependent
operations, which mayoperations, which may
act upon an abstractedact upon an abstracted
view of data.view of data.
Abstract Data Type (ADT)Abstract Data Type (ADT)
• A mathematicalA mathematical
description of an objectdescription of an object
and the set ofand the set of
operations on theoperations on the
ConceptsConcepts vs.vs. MechanismsMechanisms

8. Design and Analysis of Algorithms Chapter 2.2
8
DataStructuresDataStructures
Asymptotic AnalysisAsymptotic Analysis

9. Design and Analysis of Algorithms Chapter 2.2
9
Review: algorithm efficiency indicatorReview: algorithm efficiency indicator
order of growth
of
an algorithm’s basic operation count
the algorithm’s time efficiency

10. Design and Analysis of Algorithms Chapter 2.2
10
Asymptotic growth rateAsymptotic growth rate
A way of comparing functions that ignores constant factorsA way of comparing functions that ignores constant factors
and small input sizesand small input sizes
O(O(gg((nn)): class of functions)): class of functions t(n)t(n) that growthat grow no fasterno faster thanthan gg((nn))
ΘΘ ((gg((nn)): class of functions)): class of functions t(n)t(n) that growthat grow at same rateat same rate asas gg((nn))
ΩΩ((gg((nn)): class of functions)): class of functions t(n)t(n) that growthat grow at least as fastat least as fast asas gg((nn))

11. Design and Analysis of Algorithms Chapter 2.2
11
Big-ohBig-oh
∃c > 0, ∃n0 ≥ 0 , ∀n ≥ n0, t(n) ≤ cg(n)
t(n) ∈ O(g(n))

12. Design and Analysis of Algorithms Chapter 2.2
12
Small-ohSmall-oh
∃c > 0, ∃n0 ≥ 0 , ∀n ≥ n0, t(n) < cg(n)
t(n) ∈ o(g(n))

13. Design and Analysis of Algorithms Chapter 2.2
13
Big-omegaBig-omega
t(n) ∈ Ω(g(n))

14. Design and Analysis of Algorithms Chapter 2.2
14
Big-omegaBig-omega
∃c > 0, ∃n0 ≥ 0 , ∀n ≥ n0, t(n) ≥ cg(n)
t(n) ∈ Ω(g(n))

15. Design and Analysis of Algorithms Chapter 2.2
15
Small-omegaSmall-omega
∃c > 0, ∃n0 ≥ 0 , ∀n ≥ n0, t(n) > cg(n)
t(n) ∈ ω(g(n))

16. Design and Analysis of Algorithms Chapter 2.2
16
Big-thetaBig-theta
t(n) ∈ Θ(g(n))
∃c1>c2>0, ∃n0≥0, ∀n ≥ n0, c2g(n) ≤ t(n) ≤ c1g(n)

17. Design and Analysis of Algorithms Chapter 2.2
17
Big thetaBig theta
The reverse statement of
t(n) ∉ Θ(g(n))
∃c1>c2>0, ∃n0≥0, ∀n ≥ n0, c2g(n) ≤ t(n) ≤ c1g(n)

18. Design and Analysis of Algorithms Chapter 2.2
18
Big thetaBig theta
t(n) ∉ Θ(g(n))
∀c1>c2>0, ∀n0≥0, ∃n ≥ n0, t(n) < c2g(n) or t(n) > c1g(n)

19. Design and Analysis of Algorithms Chapter 2.2
19
Establishing rate of growth: Method 1 – using definitionEstablishing rate of growth: Method 1 – using definition
t(n)t(n) is O(is O(gg((nn)) if order of growth of)) if order of growth of t(n)t(n) ≤ order of growth≤ order of growth
ofof gg((nn) (within constant multiple)) (within constant multiple)
There exist positive constantThere exist positive constant cc and non-negative integerand non-negative integer nn00
such thatsuch that
t(n)t(n) ≤≤ c gc g((nn) for every) for every nn ≥≥ nn00
Examples:Examples:
1010nn ∈∈ O(2O(2nn22
))
55nn+20+20 ∈∈ O(10O(10nn))

20. Design and Analysis of Algorithms Chapter 2.2
20
A B O Ω Θ
1 ln2
n n ε YesYes NoNo NoNo
2 nk
cn
YesYes NoNo NoNo
3 nsinn
NoNo NoNo NoNo
4 2n
2n/2
NoNo YesYes NoNo
5 nlgc
clgn
YesYes YesYes YesYes
6 lg(n!) lg(nn
) YesYes YesYes YesYes
n
2n
∈ Ω(2n/2
) 2n
∉ Θ(2n/2
)
Establishing rate of growth: Method 1 – using definitionEstablishing rate of growth: Method 1 – using definition
Examples:Examples:

21. Design and Analysis of Algorithms Chapter 2.2
21
A B O Ω Θ
1 ln2
n n ε YesYes NoNo NoNo
2 nk
cn
YesYes NoNo NoNo
3 nsinn
NoNo NoNo NoNo
4 2n
2n/2
NoNo YesYes NoNo
5 nlgc
clgn
YesYes YesYes YesYes
6 lg(n!) lg(nn
) YesYes YesYes YesYes
n
∉ O(nsinn
) ∉ Ω(nsinn
)n n
Establishing rate of growth: Method 1 – using definitionEstablishing rate of growth: Method 1 – using definition
Examples:Examples:

22. Design and Analysis of Algorithms Chapter 2.2
22
Establishing rate of growth: Method 2 – using limitsEstablishing rate of growth: Method 2 – using limits
limlimn→∞n→∞ tt((nn)/)/gg((nn))
0 order of growth of tt((n)n) < order of growth of gg((nn))
t(n)t(n) ∈∈ o(g(n)),o(g(n)), t(n)t(n) ∈∈ O(g(n))O(g(n))
c>0 order of growth of tt((n)n) = order of growth of gg((nn))
t(n)t(n) ∈∈ ΘΘ(g(n)),(g(n)), t(n)t(n) ∈∈ O(g(n)), t(n)O(g(n)), t(n) ∈∈ ΩΩ(g(n))(g(n))
∞ order of growth of tt((n)n) > order of growth of gg((nn))
t(n)t(n) ∈∈ ωω(g(n)),(g(n)), t(n)t(n) ∈∈ ΩΩ(g(n))(g(n))
==

23. Design and Analysis of Algorithms Chapter 2.2
23
Establishing rate of growth: Method 2 – using limitsEstablishing rate of growth: Method 2 – using limits
Examples:Examples:
• loglogbb n vs. logn vs. logcc nn
loglogbbn = logn = logbbc logc logccnn
limlimn→∞n→∞( log( logbbn / logn / logccn) = limn) = limn→∞n→∞ (log(logbbc) = logc) = logbbcc
loglogbbnn ∈Θ∈Θ(log(logccn)n)

24. Design and Analysis of Algorithms Chapter 2.2
24
Exercises: establishing rate of growth – using limitsExercises: establishing rate of growth – using limits
lnln22
nn vs. lnvs. lnnn22
22nn
vs. 2vs. 2n/2n/2
22n-1n-1
vs. 2vs. 2nn
loglog22nn vs.vs. nn

25. Design and Analysis of Algorithms Chapter 2.2
25
L’Hôpital’s ruleL’Hôpital’s rule
IfIf
limlimn→∞n→∞ t(n)t(n) == limlimn→∞n→∞ gg((nn) = ∞) = ∞
The derivativesThe derivatives ff´,´, gg´ exist,´ exist,
ThenThen
t(n)t(n)
gg((nn))
limlim
nn→∞→∞
=
tt ´(´(nn))
gg ´(´(nn))
limlim
nn→∞→∞
• Example: logExample: log22nn vs.vs. nn

26. Design and Analysis of Algorithms Chapter 2.2
26
A B O Ω Θ
1 ln2
n n ε YesYes NoNo NoNo
2 nk
cn
YesYes NoNo NoNo
3 nsinn
NoNo NoNo NoNo
4 2n
2n/2
NoNo YesYes NoNo
5 nlgc
clgn
YesYes YesYes YesYes
6 lg(n!) lg(nn
) YesYes YesYes YesYes
n
Establishing rate of growthEstablishing rate of growth
Examples:Examples:

27. Design and Analysis of Algorithms Chapter 2.2
27
Stirling’s formulaStirling’s formula
n
e
n
nn )(2! π≈

28. Design and Analysis of Algorithms Chapter 2.2
28
n! v.s. nn! v.s. nnn
lg(n!) v.s. lg(nlg(n!) v.s. lg(nnn
))
Examples using stirling’s formulaExamples using stirling’s formula
ΩΩ ΘΘ OO

29. Design and Analysis of Algorithms Chapter 2.2
29
n!n! ∈∈ o(no(nnn
))
lg(n!) v.s. lg(nlg(n!) v.s. lg(nnn
))
??? lg(n!)??? lg(n!) ∈∈
o(lg(no(lg(nnn
))))
Examples using stirling’s formulaExamples using stirling’s formula
ΩΩ ΘΘ OO

30. Design and Analysis of Algorithms Chapter 2.2
30
n!n! ∈∈ o(no(nnn
))
lg(n!) v.s. lg(nlg(n!) v.s. lg(nnn
))
lg(n!)lg(n!) ∈∈ ΘΘ(lg(n(lg(nnn
))))
Examples using stirling’s formulaExamples using stirling’s formula
ΩΩ ΘΘ OO

31. Design and Analysis of Algorithms Chapter 2.2
31
Special attentionSpecial attention
n!n! ∈∈ o(no(nnn
))
However,However,
lg(n!)lg(n!) ∉∉ o(lg(no(lg(nnn
)))) lg(n!)lg(n!) ∈∈ ΘΘ(lg(n(lg(nnn
))))
sinnsinn ∈∈ ΘΘ (1/2)(1/2) sinnsinn ∈∈ O(1/2)O(1/2) sinnsinn ∈∈ ΩΩ(1/2)(1/2)
However,However,
nn1/21/2
∉∉ ΘΘ(n(nsinnsinn
)) nn1/21/2
∉∉ O(nO(nsinnsinn
)) nn1/21/2
∉∉ ΩΩ(n(nsinnsinn
))

32. Design and Analysis of Algorithms Chapter 2.2
32
Asymptotic notation propertiesAsymptotic notation properties
Transitivity:Transitivity:
f(n) =f(n) = ΘΘ(g(n)) && g(n) =(g(n)) && g(n) = ΘΘ(h(n))(h(n)) ⇒⇒ f(n) =f(n) = ΘΘ(h(n))(h(n))
f(n) = O(g(n)) && g(n) = O(h(n))f(n) = O(g(n)) && g(n) = O(h(n)) ⇒⇒ f(n) = O(h(n))f(n) = O(h(n))
f(n) = Ω(g(n)) && g(n) = Ω(h(n))f(n) = Ω(g(n)) && g(n) = Ω(h(n)) ⇒⇒ f(n) = Ω(h(n))f(n) = Ω(h(n))
If tIf t11(n)(n) ∈∈ O(gO(g11(n)) and t(n)) and t22(n)(n) ∈∈ O(gO(g22(n)), then(n)), then
tt11(n) + t(n) + t22(n)(n) ∈∈

33. Design and Analysis of Algorithms Chapter 2.2
33
Asymptotic notation propertiesAsymptotic notation properties
Transitivity:Transitivity:
f(n) =f(n) = ΘΘ(g(n)) && g(n) =(g(n)) && g(n) = ΘΘ(h(n))(h(n)) ⇒⇒ f(n) =f(n) = ΘΘ(h(n))(h(n))
f(n) = O(g(n)) && g(n) = O(h(n))f(n) = O(g(n)) && g(n) = O(h(n)) ⇒⇒ f(n) = O(h(n))f(n) = O(h(n))
f(n) = Ω(g(n)) && g(n) = Ω(h(n))f(n) = Ω(g(n)) && g(n) = Ω(h(n)) ⇒⇒ f(n) = Ω(h(n))f(n) = Ω(h(n))
If tIf t11(n)(n) ∈∈ O(gO(g11(n)) and t(n)) and t22(n)(n) ∈∈ O(gO(g22(n)), then(n)), then
tt11(n) + t(n) + t22(n)(n) ∈∈ O(max{gO(max{g11(n), g(n), g22(n)})(n)})