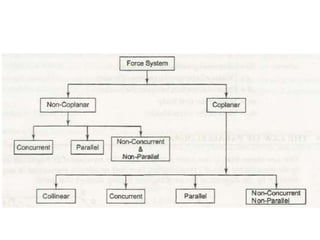
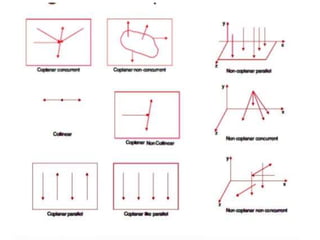
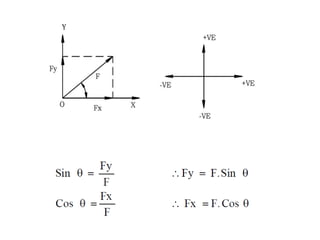
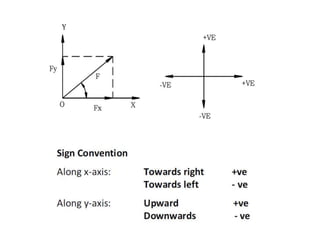
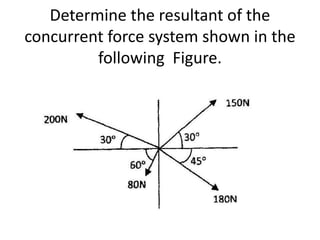
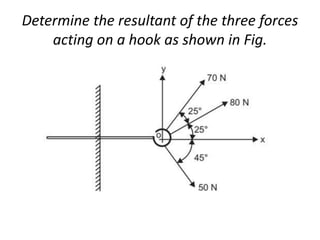
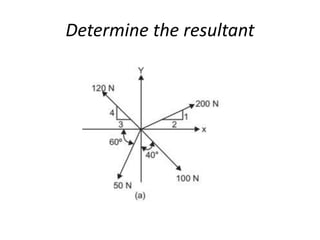
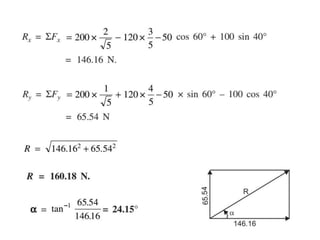
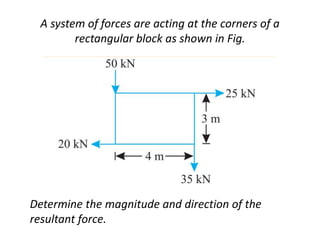
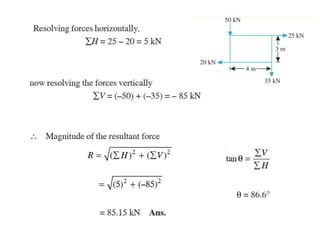
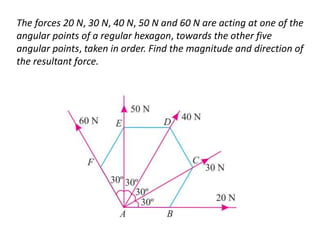
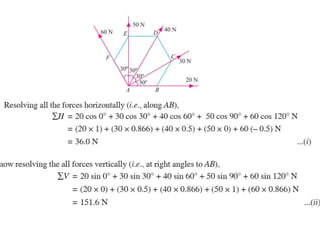
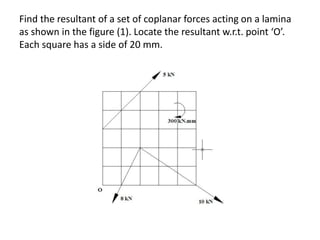
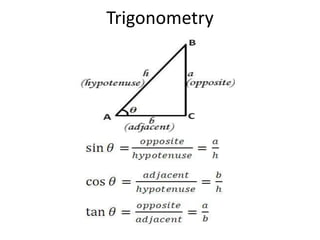
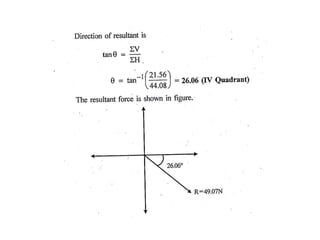
Here are the key steps to solve this problem: 1. Resolve each force into horizontal and vertical components. 2. Take the algebraic sum of the horizontal components to get the horizontal component (Fx) of the resultant. 3. Take the algebraic sum of the vertical components to get the vertical component (Fy) of the resultant. 4. Use the equations: Resultant (R) = √(Fx)2 + (Fy)2 tan(θ) = Fy/Fx to find the magnitude and direction of the resultant. 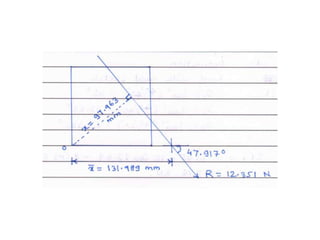5. Use Varignon's theorem to locate the position of the resultant from point O. By going through these steps, we find

1. Engineering Mechanics
Yogesh Kulkarni
(M.E Structures)
Assistant Professor
SIT CoE

2. Definition
• Mechanics is a branch of the physical sciences
that is concerned with the state of rest or
motion of bodies subjected to the action of
forces
• It is the branch of science which deals with a
system of forces and their effect on the
bodies.
• It is divided into statics and dynamics.

3. Basic Concepts
• Space is the region occupied by the bodies. We
set up an coordinate system to specify where the
object is by the position and its posture by the
orientation.
• Time is the measure of the succession of events.
Often, we are more interested in the change of
physical quantities with respect to time instead of
time variable itself.
• Force is an external agency which changes or
tends to change the state of the body. (Vector
Quantity) Newton N as S.I units

4. • Particle is a body of which its dimension is
negligible. The rotation effect is insignificant
because it is just a point.
• Whether the body can be treated as the
particle or not depends on the relative
dimensions in the problem and how much
detailed of the solution we are interested in.

5. • Rigid body is a body whose relative
movement between its parts are negligible
relative to the gross motion of the body. For
example the motion of an ingot can be
analyzed by assuming the object being rigid.

6. • Non rigid body is a body whose relative
movement between its parts are significant
relative to the gross motion of the body.
• Knowledge of the mechanics of the
deformable material must be used along with
Dynamics in order to determine the absolute
motion of the non rigid bodies.

7. Engineering Mechanics
Rigid-body Mechanics
• a basic requirement for the study of the
mechanics of deformable bodies and the
mechanics of fluids (advanced courses).
• essential for the design and analysis of many
types of structural members, mechanical
components, electrical devices, etc,
encountered in engineering.
A rigid body does not deform under load!

8. 1 - 8

9. Mechanics
Statics
Dynamics
Kinematics Kinetics

10. Engineering Mechanics
• Statics: deals with equilibrium of bodies under
action of forces (bodies may be either at rest or
move with a constant velocity).

11. Engineering Mechanics
• Dynamics: deals with motion of bodies
(accelerated motion)

12. • Kinematics : Branch of dynamics which deals
with the study of system of forces and their
effects on bodies in motion without
considering mass of the body and forces
which causes the motion
• Kinetics : Branch of dynamics which deals with
the study of system of forces and their effects
on bodies in motion considering mass of the
body and forces which causes the motion

16. Scalars and Vectors
• Scalars: only magnitude is associated.
Ex: time, volume, density, speed, energy,
mass
• Vectors: possess direction as well as
magnitude, and must obey the
parallelogram law of addition
(and the triangle law)
Ex: displacement, velocity, acceleration,
force, moment, momentum

17. Trigonometry

18. Force
• Force is an external agency which changes or
tends to change the state of the body. (Vector
Quantity) Newton N as S.I units
• Characteristics of force
1. Magnitude(unit)
2. Direction(angle)
3. Sense of nature(arrowhead)
4. Point of application.

24. RESULTANT:
• Is the single force which will produce the same
effect (in magnitude and direction) as it is
produced by number of forces acting together.
• Thus, the resultant is a single force, which will
give the same result as it is produced by the
number of forces acting on a body. Thus, we can
replace all the forces by the resultant. In other
words, we can say that, the resultant is the
combined effect of all the forces acting on the
body (in magnitude and direction).

25. HOW TO FIND THE RESULTANT OF A
GIVEN FORCE SYSTEM
A. The Resultant of TWO coplanar concurrent forces:
Triangle law of forces.
Parallelogram law of forces.
B. The Resultant of THREE OR MORE coplanar concurrent
forces:
Polygon law of forces (Graphical method).
Method of resolution and composition of forces.
C. The Resultant of THREE OR MORE non-concurrent forces:
Analytical method by using Varignon’s theorem of moments.
Graphical method.

26. • TRIANGLE LAW OF FORCES: “If two or
concurrent forces are represented by two sides
of a triangle taken in order, then the resultant
of the two forces shall be given by the third
side of the triangle taken in opposite order”

27. • PARALLELOGRAM LAW OF FORCES: “If two
coplanar concurrent forces acting at and
away from the point and are represented by
the two adjacent sides of a parallelogram in
magnitude and direction, then the resultant is
given by the diagonal of the parallelogram
passing through the same common point”

28. PARALLELOGRAM LAW OF FORCES

29. • POLYGON LAW OF FORCES:
• “If ’n ’is the number of coplanar concurrent
forces and these are represented by ‘n’ sides
of a polygon taken in order, then the resultant
of the given ‘n’ forces shall be given by the
closing (n+1) th side of the polygon taken in
reverse order”

30. Two forces of 100 N and 150 N are
acting simultaneously at a point. What
is the resultant of these two forces, if
the angle between them is 45°?
Problem

31. Solution
• First force (F1) = 100 N;
• Second force (F2) = 150 N and angle between
• F1 and F2 (θ) = 45°.

33. Resolution of Forces
• Resolution: The method of splitting a given
force into its components, without changing
its effect on the body.
• Generally, it is convenient to resolve the force
along x and y axis. These components along x
and y axis are known as Orthogonal
Components.

36. Steps to find the Resultant of
Concurrent Forces

37. Determine the resultant of the
concurrent force system shown in the
following Figure.

40. Determine the resultant of the three forces
acting on a hook as shown in Fig.

42. Determine the resultant

45. Moment

47. Moment = Force x Perpendicular Distance
M = F x d
(Nm) = (N) x (m)

51. Varignon’s Theorem of Moments

53. Steps To Find Resultant
of Non-Concurrent Forces
1. Resolve all the forces horizontally and find the algebraic sum of all the horizontal components (Σ
Fx). Here, Σ Fx represents the horizontal component of the resultant.
2. Resolve all the forces vertically and find the algebraic sum of all the vertical components (Σ Fy).
Here, Σ Fy represents the vertical component of the resultant.
3. Resultant ‘R’ is given by the equation,    2
2
R Fy
Fx 



4. Let, α be the angle made by the resultant ‘R’ with the horizontal, then
Fx
Fy
tan





54. 1. Select some reference point (say point A) and take moments of all the forces about that point
using correct sign conventions.
2. Find algebraic sum of moments of all forces about the reference point ( A
M
 )
3. Let, ‘x’ be the perpendicular distance between the resultant and the reference point. Take
moment of the resultant about the reference point (MRA).
4. Apply Varignon’s theorem of moments to find the position (i.e. distance x) of the resultant about
the reference point.
Note:
1. If A
M
 is + ve, then the resultant will produce clockwise moment about the reference point.
If A
M
 is - ve, then the resultant will produce anti- clockwise moment about the reference point.

55. COUPLE
• Two equal, opposite and parallel forces acting
on a body form a couple.
• As the two forces are equal and opposite,
their resultant is zero, but they will produce
rotational effect i.e. they will create the
moment.

56. Properties of a Couple:
1. Couple can be replaced by a single force.
2. Couple cannot produce translatory motion (straight line motion) but it can produce rotation.
3. Moment of a couple = force x lever arm.
4. The moment of a couple is independent of the position of moment centre and it remains
constant.
e.g. from figure, ΣMA = P x a
ΣMO = (P x OB) – ( P x OA) = P ( OB – OA)
ΣMO = P x a

57. 10 N
Anticlockwise (- ve)
10 N
A 2 m
M = 10 x 2 (Anticlockwise)
= -20 Nm
Moment = Force x Perpendicular
Distance
A 2 m

58. A 2 m
10 N
A
10 N
M = 10 x 0
= 0 Nm
Moment = Force x Perpendicular
Distance

59. A system of forces are acting at the corners of a
rectangular block as shown in Fig.
Determine the magnitude and direction of the
resultant force.

61. The forces 20 N, 30 N, 40 N, 50 N and 60 N are acting at one of the
angular points of a regular hexagon, towards the other five
angular points, taken in order. Find the magnitude and direction of
the resultant force.

64. Find the resultant of a set of coplanar forces acting on a lamina
as shown in the figure (1). Locate the resultant w.r.t. point ‘O’.
Each square has a side of 20 mm.