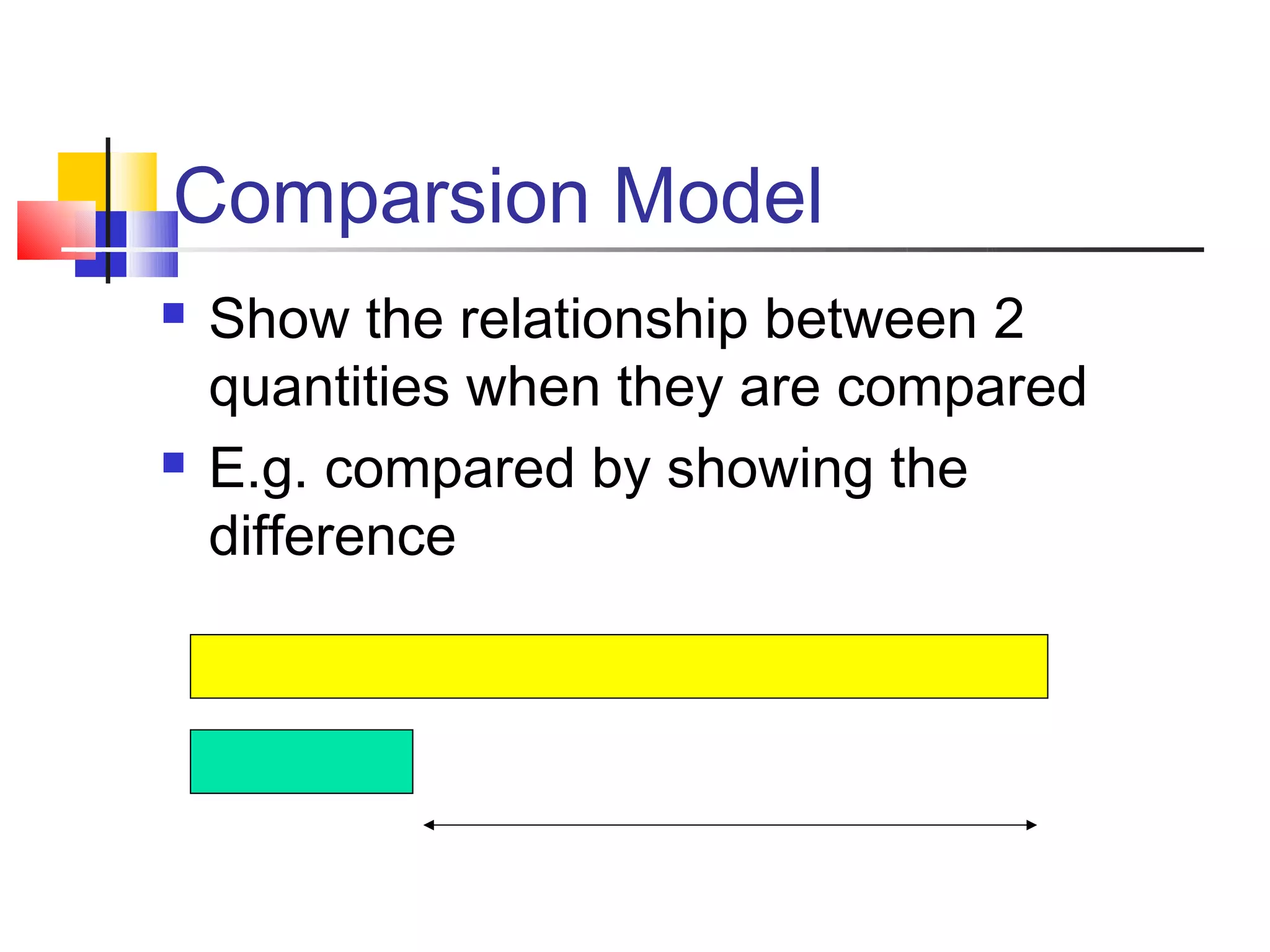
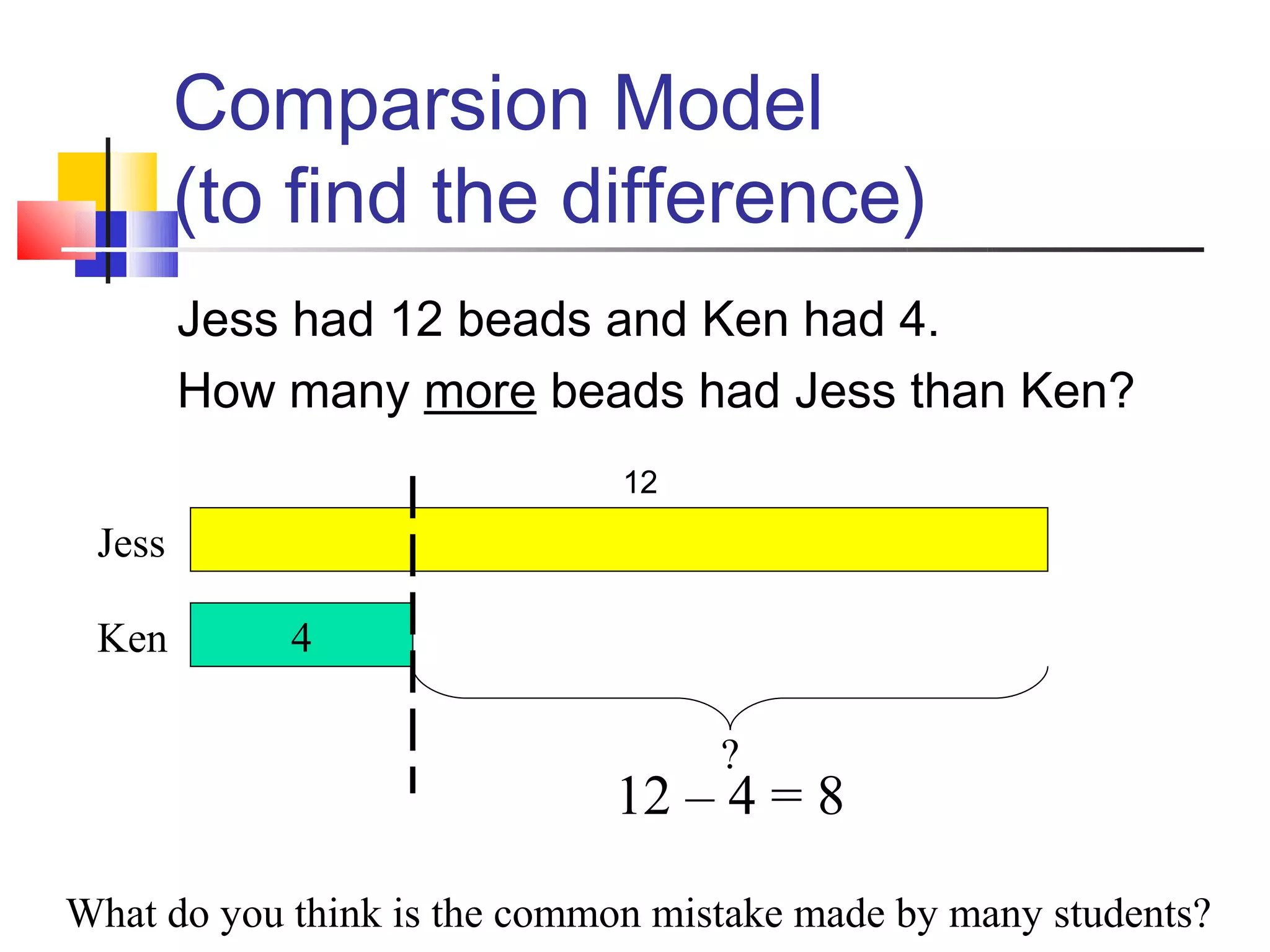
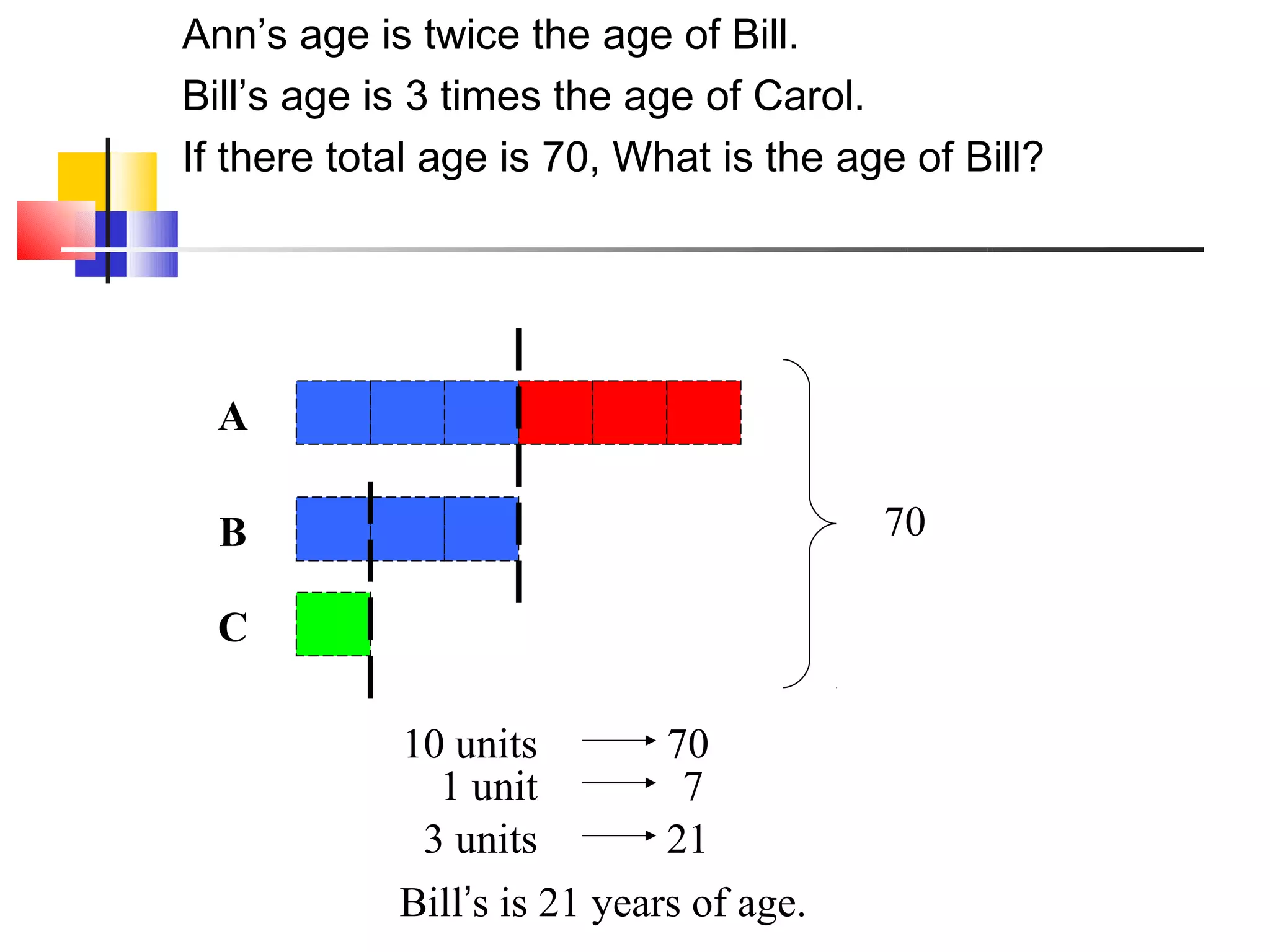
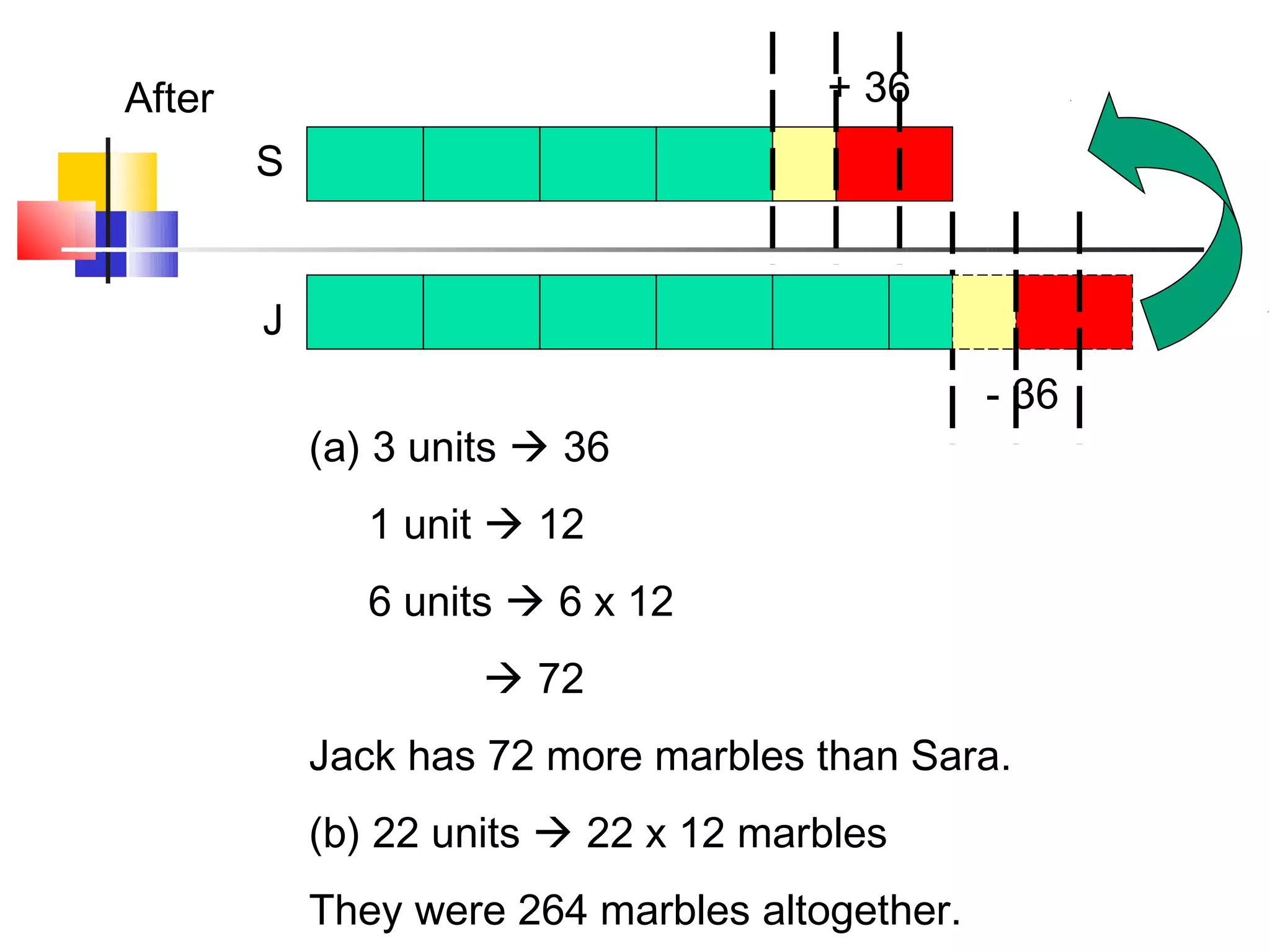
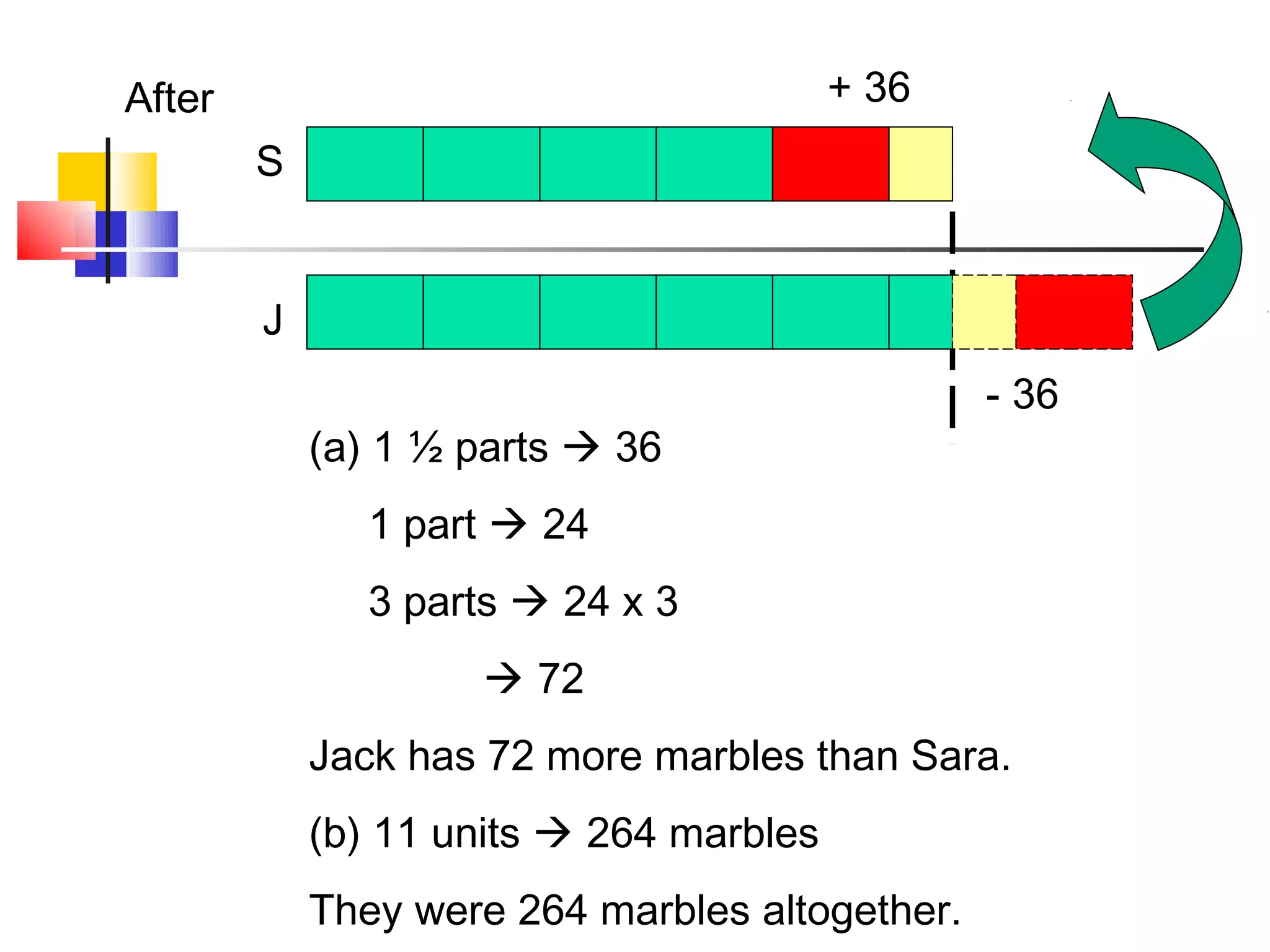
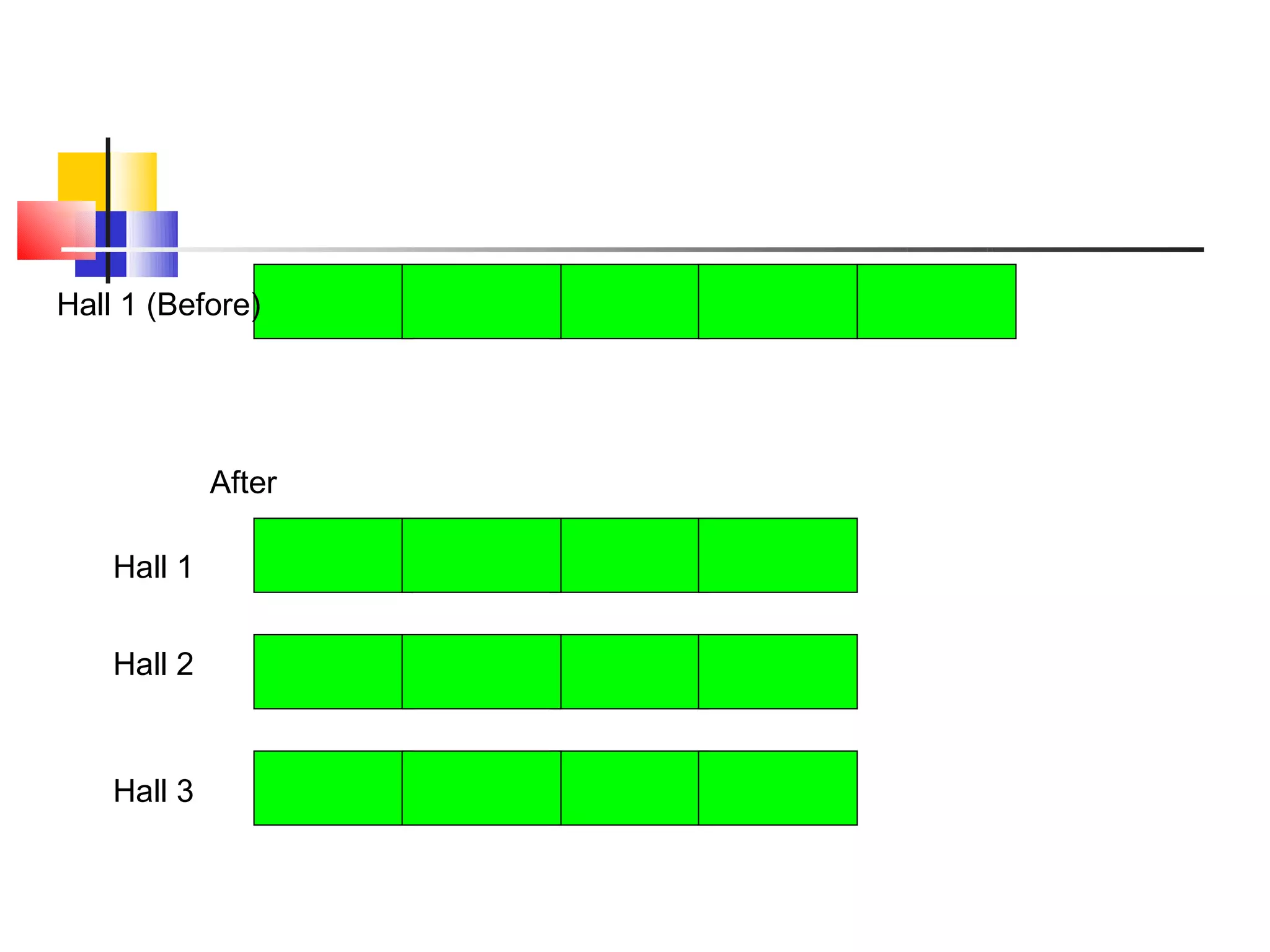
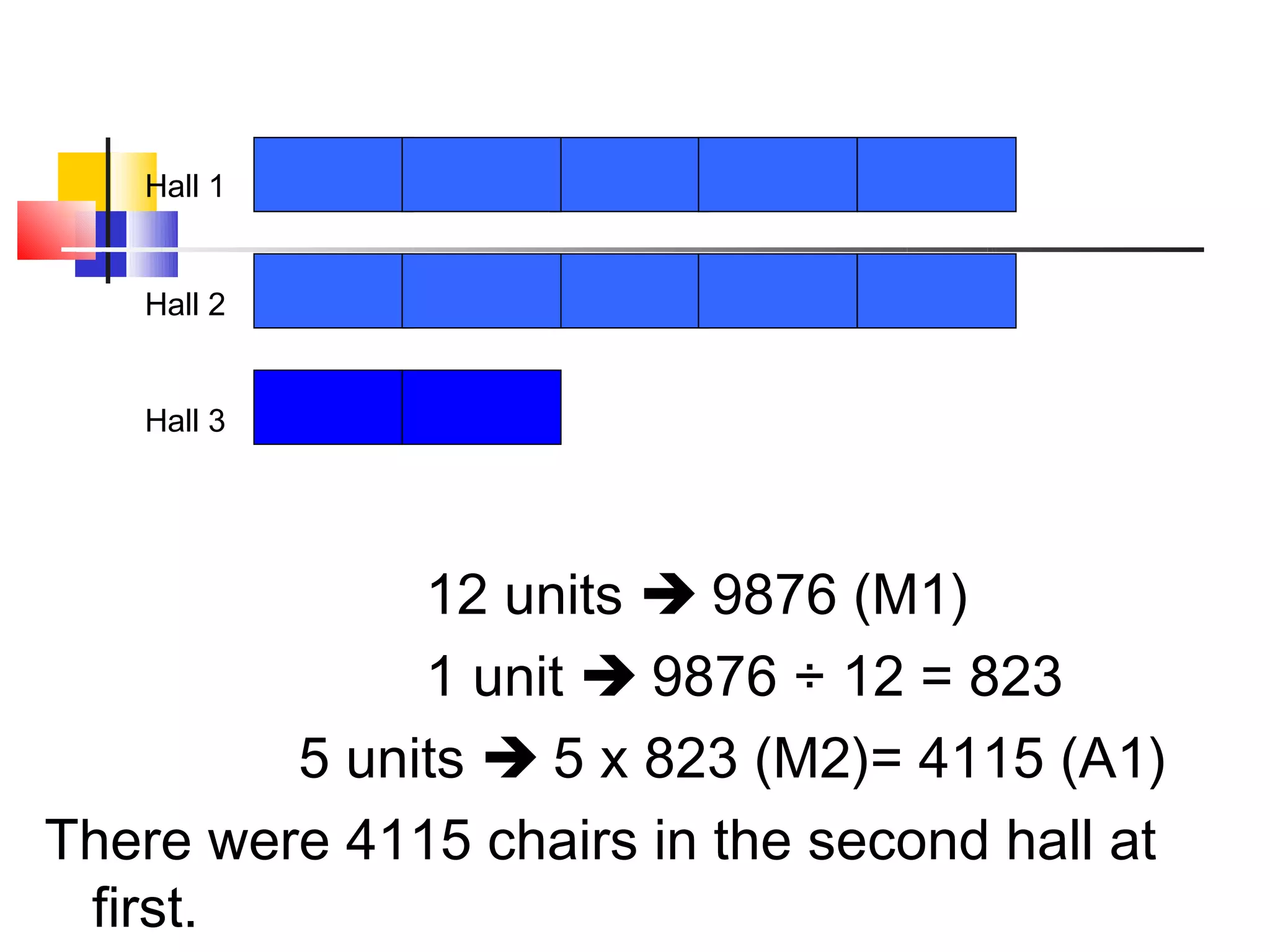
The document discusses bar models, a method for representing word problems pictorially using bars or diagrams. It was developed in the 1980s to help students in primary school who struggle with word problems. Bar models use pictures to represent quantities and relationships, making problems more visual and intuitive. They are particularly effective for younger students. The document outlines different types of bar models, including part-whole, comparison, and change models. It provides guidelines for constructing bar models and examples of using models to solve a variety of word problems.

1. Bar Models for Elementary
Grades
Peggy Foo
Marshall Cavendish Institute

2. Learning Outcomes
Participants should be able to
 understand the rationale of model method
as a heuristic/ problem-solving tool.
 Draw different types of models to solve a
variety of word problems.

3. Origin
Developed by a project team in MOE in the 1980s
Objective: Help students who have great difficulty with
word problems in the early years of primary school.
Drawing a pictorial model to represent mathematical
quantities (known and unknowns) and their relationships
given in a problem.

4. Rationale
The Mathematics Curriculum Framework focuses on
mathematical problem solving.
Reasoning,
communication
and connections

5. Under ‘Processes’ component,
 One of the heuristics is model method
 Helps to visualize situations and
Maths problems which are usually
meant for secondary pupils

6. Differences
Model Method Algebraic Method
_________ representation Abstract reasoning
More effective for _______ More suitable for older
pupils who need to see to pupils
understand
Foundation for algebraic Use of abstract symbol
thinking (without the use of
abstract symbol)

7. Differences
Model Method Algebraic Method
Pictorial representation Abstract reasoning
More effective for younger More suitable for older
pupils who need to see to pupils
understand
Foundation for algebraic Use of abstract symbol
thinking (without the use of
abstract symbol)

8. Guidelines
 Represent the problem using bar(s)
 The bar(s) are best drawn proportionately
 Fill in the diagram with all the given
information
 The unknown value/ answer is represented
by question mark
 Interpret the model and write a simpler
mathematical statement
(e.g. 11 units + 40  84)

9. Different types of models
 Part-Whole Model
 Comparative Model
 Change/ Transforming Model

10. Part-Whole Model
♠ Shows various parts which make up a
whole
♠ Find the whole by addition
♠ Find the other part by subtraction

11. Part-Whole Model
(using concrete materials)
Ann had 5 books.
Bill gave her 7 more books.
How many books did Ann have altogether?

12. Part-Whole Model
?
John has 20 marbles
He gave 3/5 of it to Peter.
How many marbles did John give to Peter?

13. Part-Whole Model
?
John has 20 marbles
He gave 3/5 of it to Peter.
How many marbles did John give to Peter?
20
5 unit  20 marbles
1 unit  4 sweets
3 units  3 x 4
= 12
John gave 12 marbles to Peter.

14. Comparsion Model
 Show the relationship between 2
quantities when they are compared
 E.g. compared by showing the
difference

15. Comparsion Model (Try it)
Alice had 3 books.
She had 9 books less than Beth.
How many books did Beth have?

16. Comparsion Model
Alice had 3 books.
She had 9 books less than Beth.
How many books did Beth have?
Alice 3 9
Beth
? 3 + 9 = 12
What do you think is the common mistake made by many students?

17. Comparsion Model
(to find the difference)
Jess had 12 beads and Ken had 4.
How many more beads had Jess than
Ken?

18. Comparsion Model
(to find the difference)
Jess had 12 beads and Ken had 4.
How many more beads had Jess than Ken?
12
Jess
Ken 4
?
12 – 4 = 8
What do you think is the common mistake made by many students?

19. Model drawing promotes conceptual
understanding via visual representations
rather than “cue words” method.
More than ≠ use addition
Less than ≠ use subtraction

20. Comparsion Model
Ann’s age is twice the age of Bill.
Bill’s age is 3 times the age of Carol.
If there total age is 70, What is the age of Bill?

21. Ann’s age is twice the age of Bill.
Bill’s age is 3 times the age of Carol.
If there total age is 70, What is the age of Bill?
A
B 70
C
10 units 70
1 unit 7
3 units 21
Bill’s is 21 years of age.

22. Change/ Transforming Model
 This type of model can be used to solve
complex problems
 The parts can be transformed into
smaller units.
 This type of model is useful for tacking
problems which involve before-and-
after situations.

23. At first, Sara had 4/7 of the number of marbles
Jack had. When Sara received 36 marbles from
Jack, both had the same number of marbles.
(a) How many more marbles did Jack have
than Sara at first?
(b) How many marbles were there
together?

24. At first, Sara had 4/7 of the number of marbles Jack had.
When Sara received 36 marbles from Jack,
both had the same number of marbles.
(a) How many more marbles did Jack have than Sara at first?
(b) How many marbles were there together?
Before
S
J

25. After + 36
S
J
- 36
(a) 3 units  36
1 unit  12
6 units  6 x 12
 72
Jack has 72 more marbles than Sara.
(b) 22 units  22 x 12 marbles
They were 264 marbles altogether.

26. After + 36
S
J
- 36
(a) 1 ½ parts  36
1 part  24
3 parts  24 x 3
 72
Jack has 72 more marbles than Sara.
(b) 11 units  264 marbles
They were 264 marbles altogether.

27. Three halls contained 9,876 chairs
altogether. One-fifth of the chairs were
transferred from the first hall to the
second hall. Then, one-third of the
chairs were transferred from the second
hall to the third hall and the number of
chairs in the third hall doubled. In the
end, the number of chairs in the three
halls became the same. How many
chairs were in the second hall at first?

28. Hall 1 (Before)
After
Hall 1
Hall 2
Hall 3

29. After
Hall 1
Hall 2
Hall 3
Before
Hall 1
Hall 2
Hall 3

30. Hall 1
Hall 2
Hall 3
12 units  9876 (M1)
1 unit  9876 ÷ 12 = 823
5 units  5 x 823 (M2)= 4115 (A1)
There were 4115 chairs in the second hall at
first.

31. Thank you