1) The document provides a mathematics curriculum guide for first grade addition, subtraction, and number systems. It outlines big ideas, essential questions, unit vocabulary, and Arizona state standards to be covered.
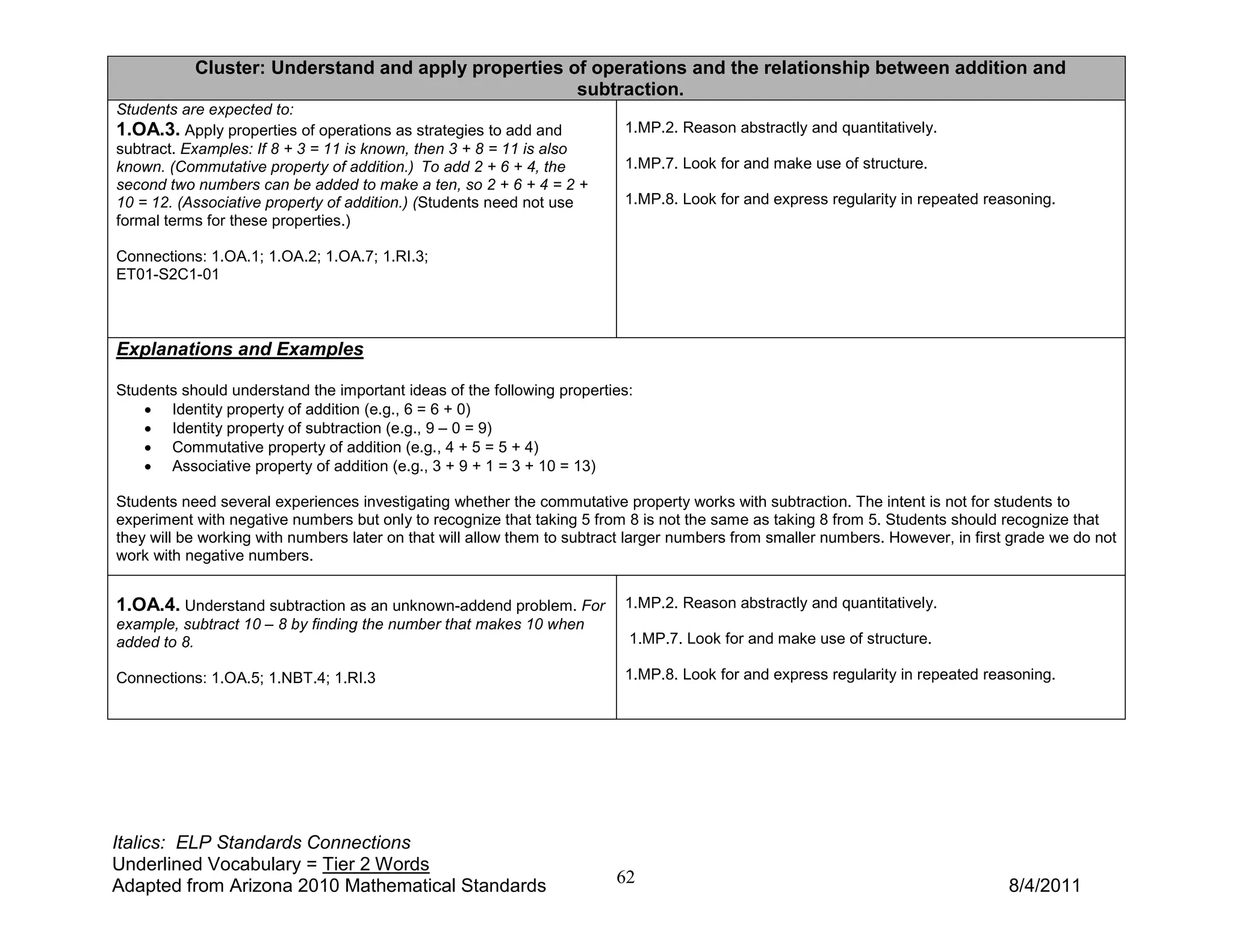
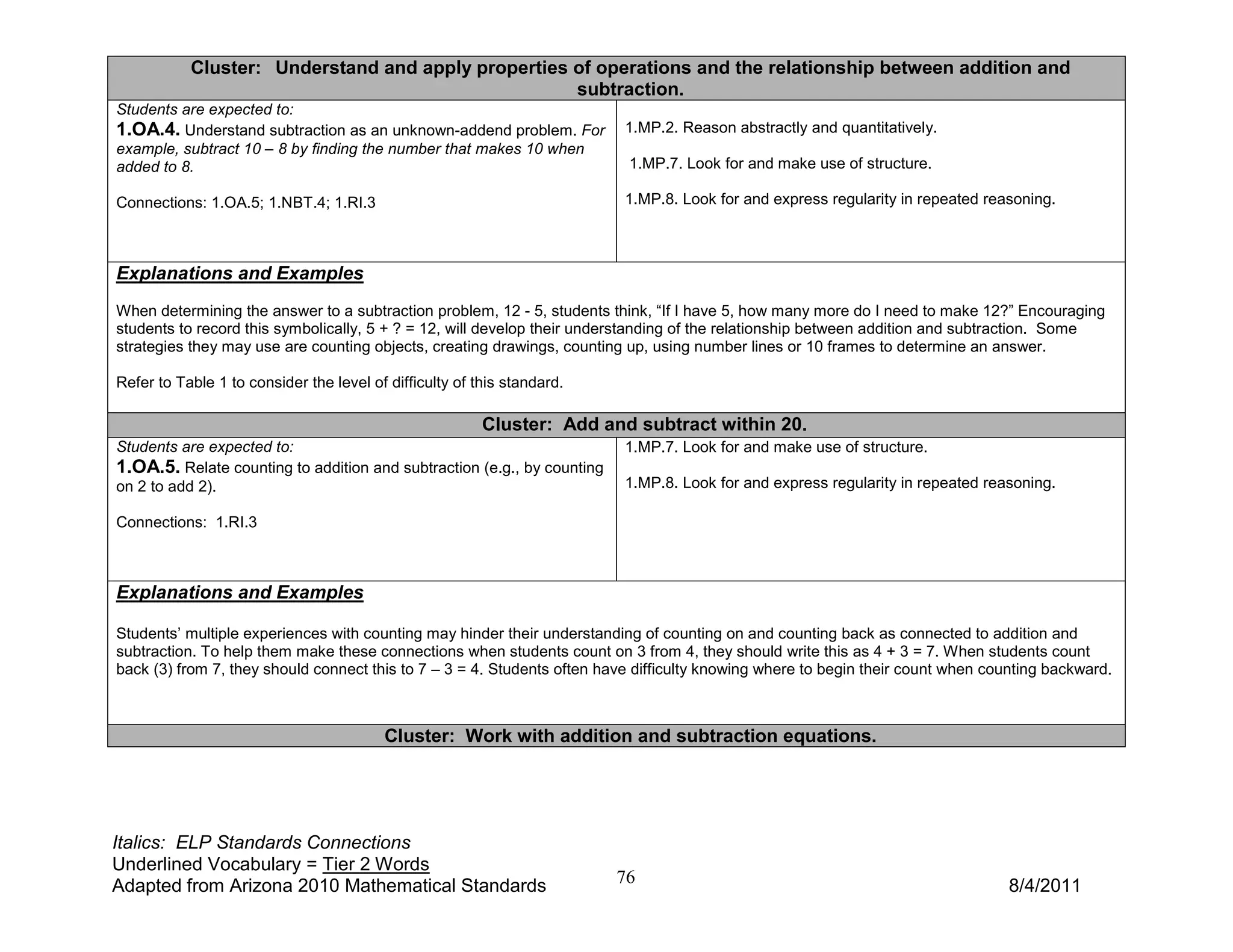
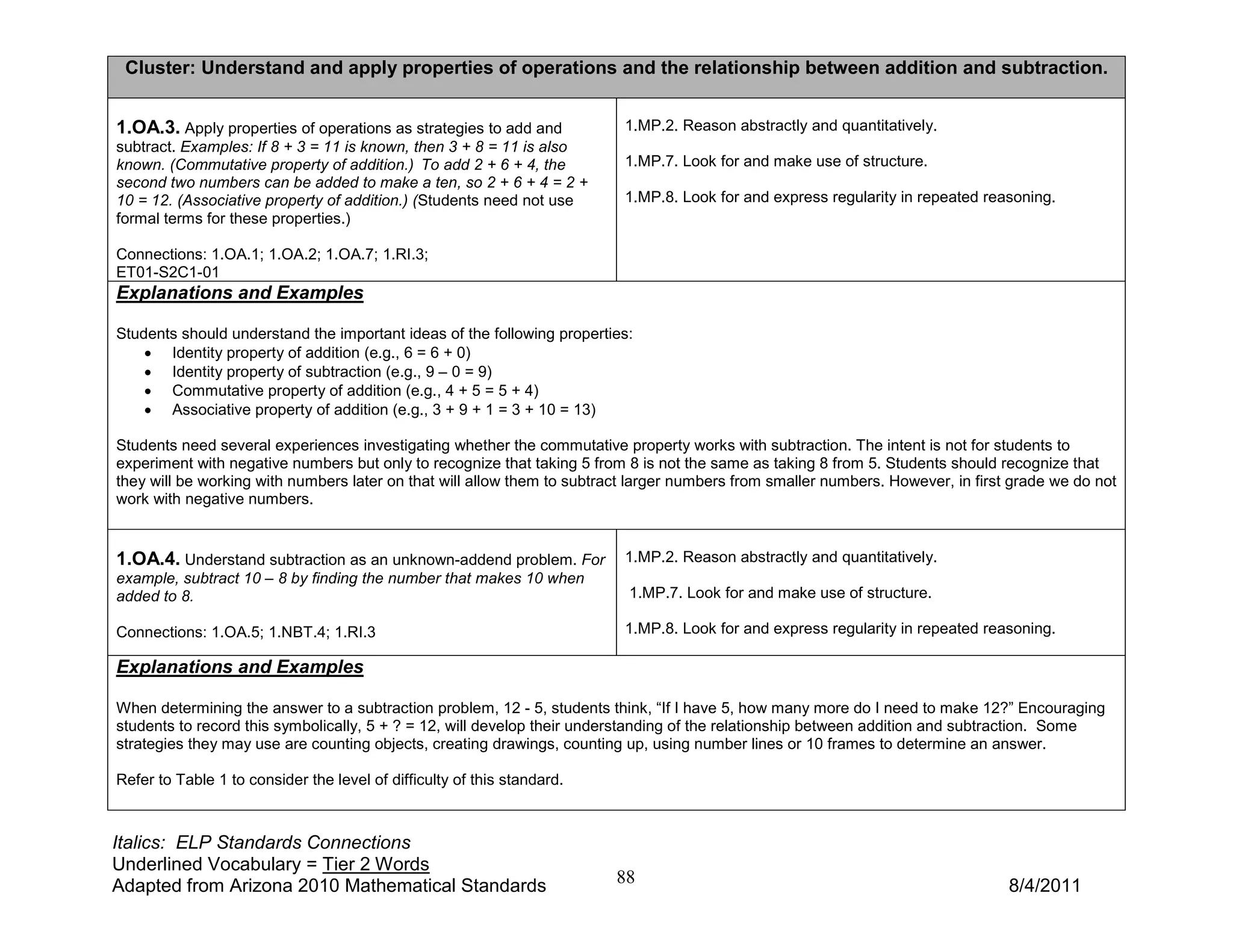
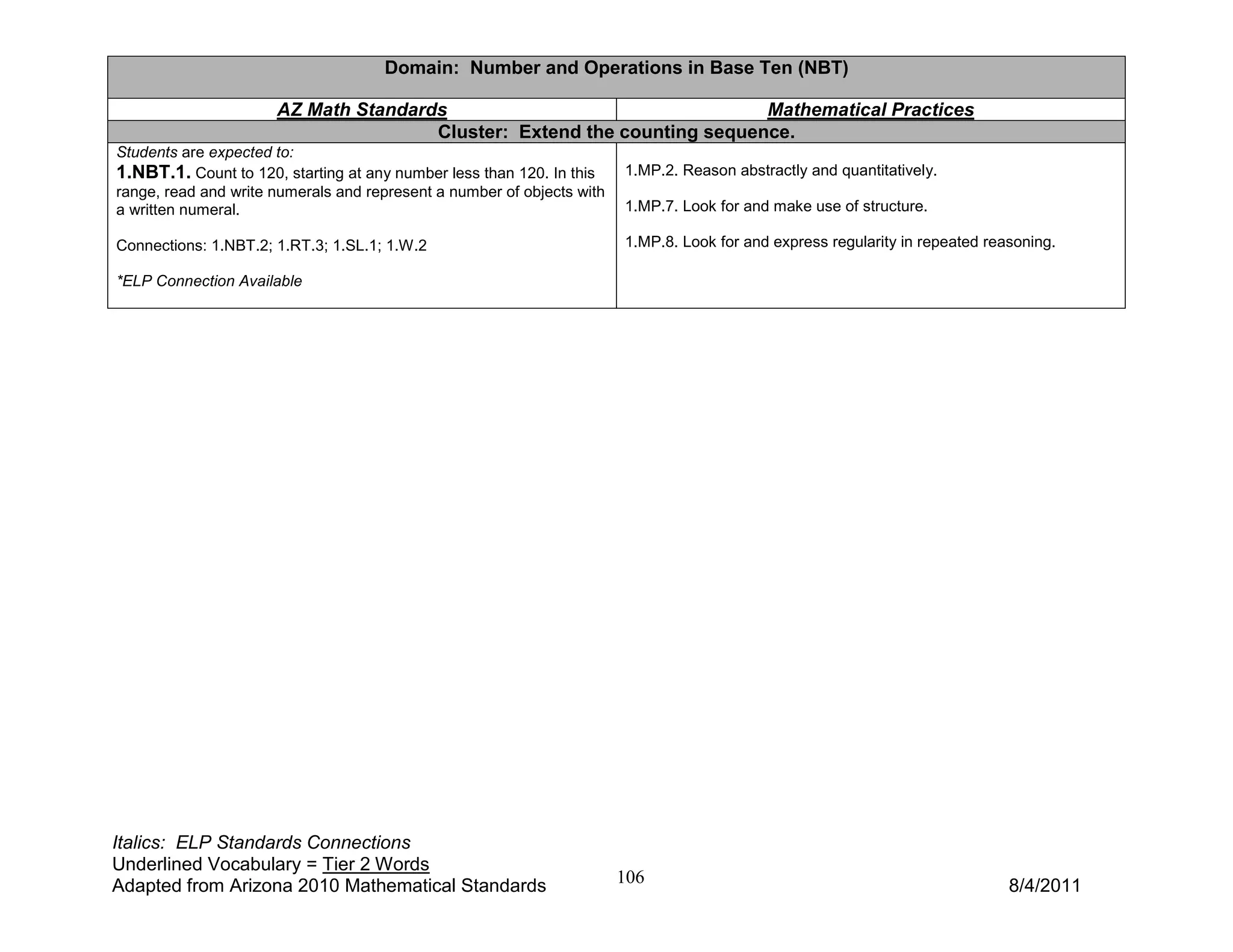
2) Key concepts include counting quantities, comparing numbers, and composing and decomposing numbers. Students will learn strategies for addition and subtraction word problems involving combining, separating, and comparing quantities.
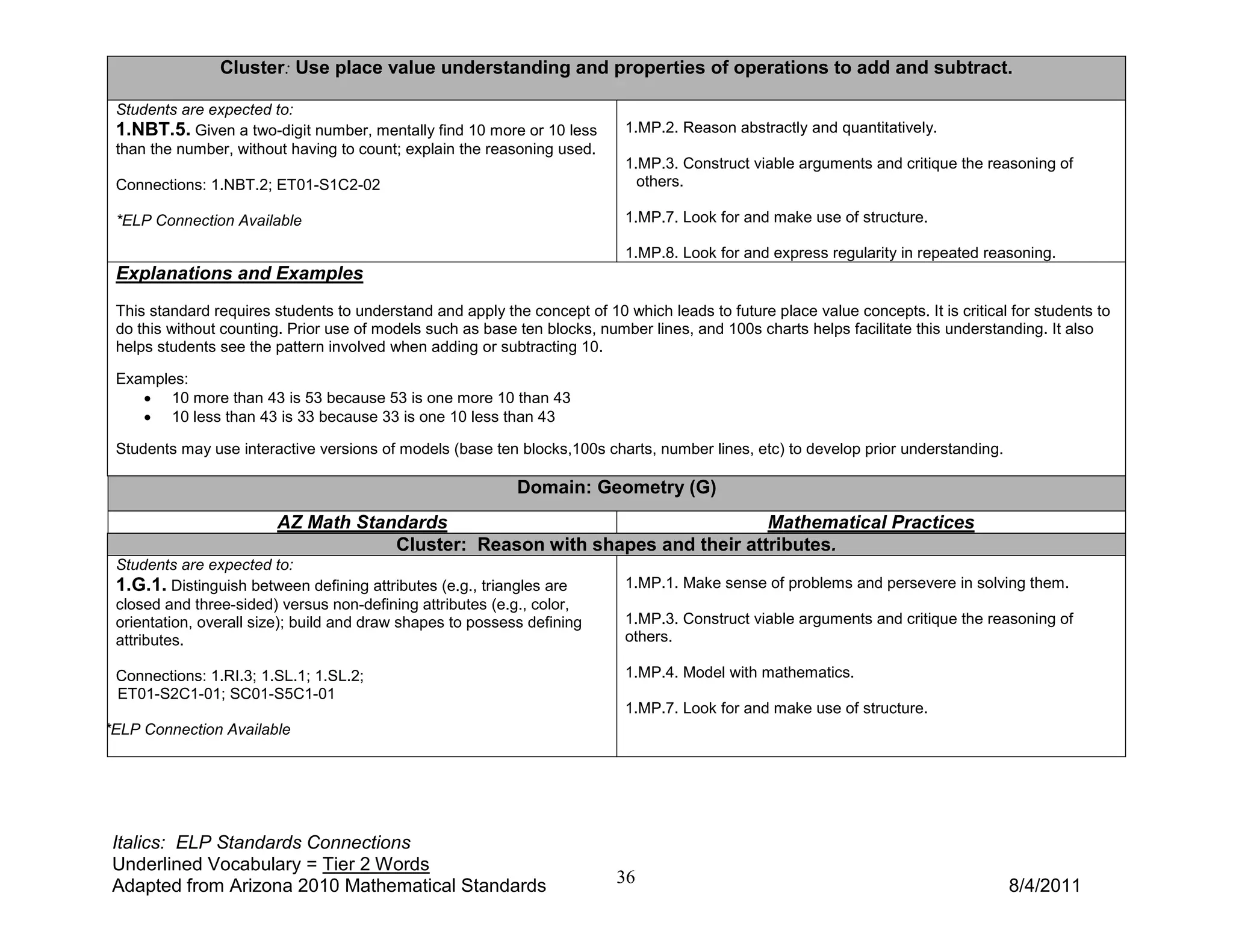
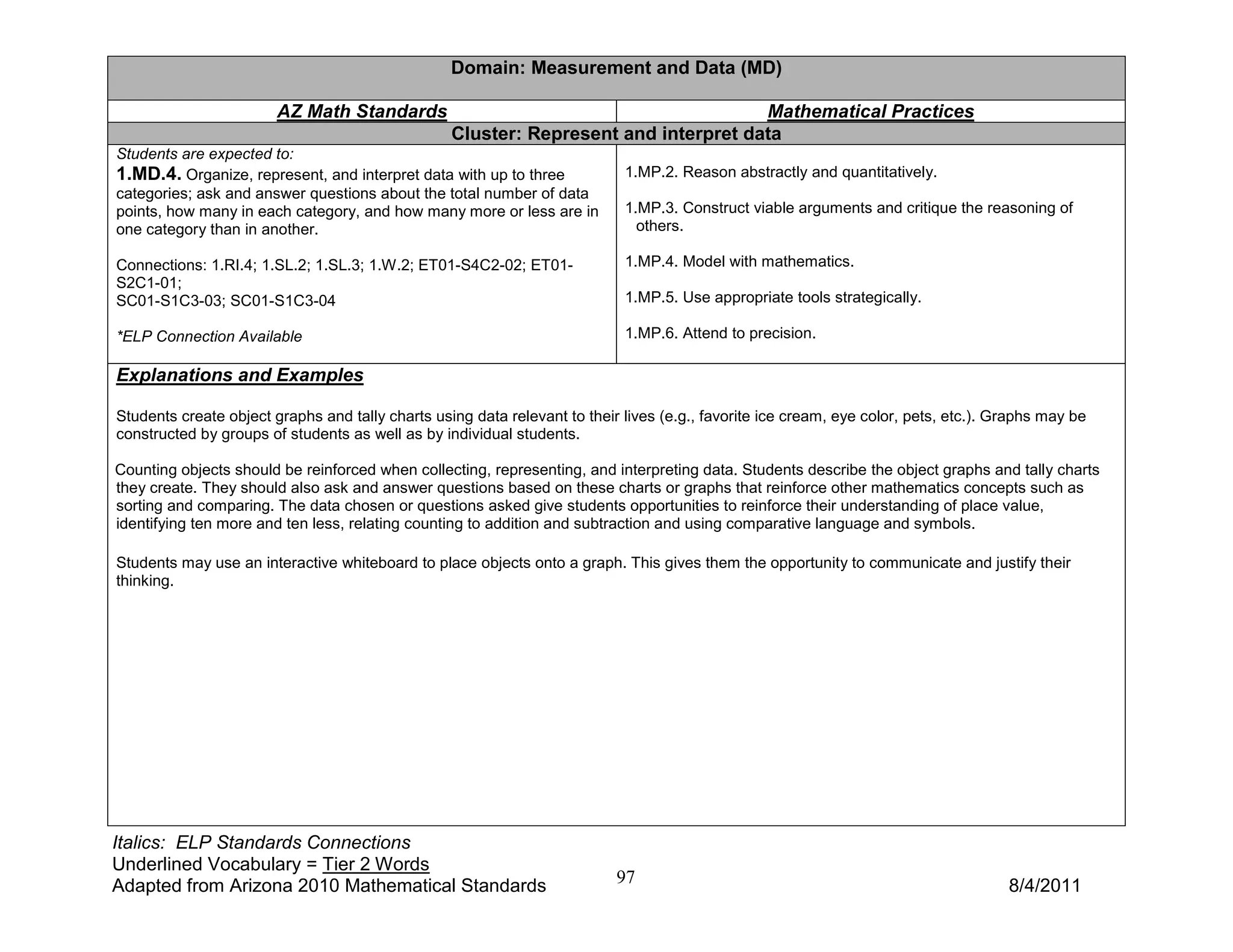
3) The guide provides examples and explanations for how students can use objects, drawings, and equations to represent addition and subtraction word problems involving unknown values in different positions. It emphasizes developing fluency with addition and subtraction facts to 10.