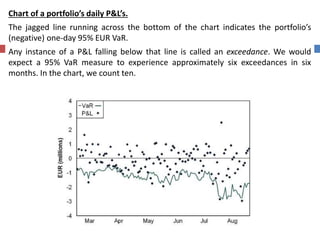
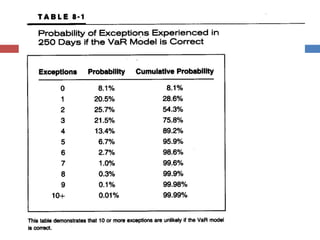
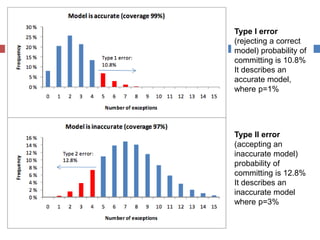
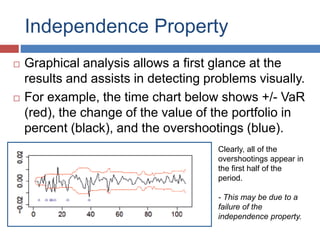
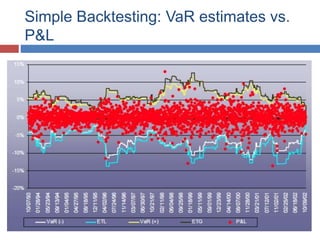
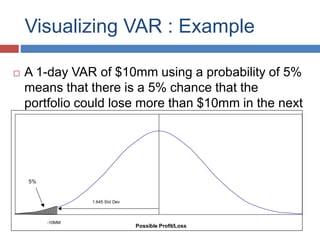
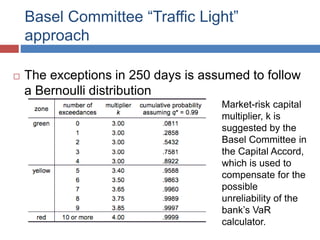
The document discusses Value-at-Risk (VaR) models and backtesting methods used to evaluate VaR estimates. Backtesting compares predicted VaR losses to actual losses to identify instances where VaR was underestimated. The results can refine VaR models to improve accuracy and reduce unexpected losses. Proper backtesting assesses whether exceedance frequencies match confidence levels and whether results appear independent over time.

1. MEASUREMENT ERRORS
AND BACKTESTING
METHODS
Group 2

2.  Value-at-Risk (VaR) is a risk model which
predicts the loss that an investment portfolio
may experience over a period of time.

 In order to evaluate the quality of the VAR
estimates, the models should always be
backtested with appropriate methods.

3. Backtesting
 A technique used to compare the predicted losses from VaR
with the actual losses realised at the end of the period of
time.
 This identifies instances where VaR has been
underestimated, meaning a portfolio has experienced a loss
greater or than the original VaR estimate.
 The results of the Back Testing can be used to refine the
models used for the VaR predictions, making them more
accurate and reducing the risk of unexpected losses.

4. Chart of a portfolio’s daily P&L’s.
The jagged line running across the bottom of the chart indicates the portfolio’s
(negative) one-day 95% EUR VaR.
Any instance of a P&L falling below that line is called an exceedance. We would
expect a 95% VaR measure to experience approximately six exceedances in six
months. In the chart, we count ten.

5. Key Points of Back Testing Value-at-
Risk
1. The following minimum standards apply to calculating
capital charge within a model measuring market risk;
2. Data sets should be updated at least once every 3
months
3. VaR must be calculated on a daily basis
4. 99th percentile, one-tailed confidence interval is to be
used
5. A 10 day movement in prices should be used as the
instant price shock
6. 1 year is classified as a minimum period for “historical”
observations

6.  For example, if the confidence level used for
calculating daily VaR is 99%, we expect an
exception to occur once in every 100 days on
average.
 In the backtesting process, we could
statistically examine whether the frequency of
exceptions over some specified time interval is
in line with the selected confidence level.

7. Research to date has focused on VaR measures used by
banks. Published backtesting methodologies mostly fall into
three categories:
 Coverage tests – assess whether the frequency of
exceedances is consistent with the quantile of loss a VaR
measure is intended to reflect.
 Distribution tests – are goodness-of-fit tests applied to
the overall loss distributions forecast by complete VaR
measures.
 Independence tests – assess whether results appear
to be independent from one period to the next.

8.  In this respect, an accurate VaR model needs
to satisfy the so-called Unconditional
Coverage Property.
 Unconditional Coverage – refers to the fact
that the fraction of overshootings obtained
should be in line with the confidence level of
VaR.
 Failure of unconditional coverage means that
the calculated VaR does not measure the risk
accurately.

9. Unconditional Coverage
 Denoting the number of exceptions as x and the
total number of observations as T:
 We may define the failure rate as x/T.
 In an ideal situation, this rate would reflect the
selected confidence level.
 For instance, if a confidence level of 99 % is used,
we have a null hypothesis that the frequency of
tail losses is equal to p = (1-c) = 1-0.99 = 1%.
 Assuming that the model is accurate, the
observed failure rate x/T should act as an
unbiased measure of p, and thus converge to 1%

10.  Each trading outcome either produces a VaR
violation exception or not. This sequence of
‘successes and failures’ is commonly known
as Bernoulli trial.
 The number of exceptions, x ,follows a
binomial probability distribution:

12.  By utilizing this binomial distribution we can
examine the accuracy of the VaR model.
 However, when conducting a statistical
backtest that either accepts or rejects a null
hypothesis (of the model being ‘good’), there is
a tradeoff between two types of errors.

13.  Type I errors occur when we reject the model
which is correct, while Type II errors occur
when we fail to reject (that is incorrectly
accept) the wrong model.
 It is clear that in risk management, it can be
much more costly to incur in type II errors, and
therefore we should impose a high threshold in
order to accept the validity of any risk model.

14. Type I error
(rejecting a correct
model) probability of
committing is 10.8%
It describes an
accurate model,
where p=1%
Type II error
(accepting an
inaccurate model)
probability of
committing is 12.8%
It describes an
inaccurate model
where p=3%

15. Independence Property
 Besides unconditional coverage, VaR should satisfy
the independence property.
 Independence property – refers to the clustering of
overshootings.
 If the market conditions change, the VaR model
should adapt quickly to the new situations.
 Therefore, observing an overshooting tomorrow
should be independent of observing an overshooting
today.
 Series of overshootings – means that the risk is
underfunded for prolonged periods during episodes of
increased risk.

16. Independence Property
 Graphical analysis allows a first glance at the
results and assists in detecting problems visually.
 For example, the time chart below shows +/- VaR
(red), the change of the value of the portfolio in
percent (black), and the overshootings (blue).
Clearly, all of the
overshootings appear in
the first half of the
period.
- This may be due to a
failure of the
independence property.

17. Simple Backtesting: VaR estimates vs.
P&L

18.  The simplest backtest consist of counting the number of
exceptions (losses larger than estimated VaR) for a given
period and comparing to the expected number for the chosen
confidence interval.
 A more rigorous way to perform the backtesting analysis is to
determine the accuracy of the model predicting both the
frequency and the size of expected losses.
 Backtesting Expected Tail Loss (ETL) or Expected Tail
Gain (ETG) numbers can provide an indication of how well
the model captures the size of the expected loss (gain)
beyond VaR, and therefore can enhance the quality of the
backtesting procedure.

19. Backtesting
- Statistical testing that consist of checking whether
actual trading losses are in line with the VAR
forecasts
In its simplest form, the backtesting procedure
consists of calculating the number or percentage of
times that the actual portfolio returns fall outside
the VaR estimate, and comparing that number to
the confidence level used.
 The Basel back-testing framework consists in recording
daily exception of the 99% VAR over the last year
 Even though capital requirements are based on 10 days
VAR, back testing uses a daily interval, which entails more

20.  On average, one would expect 1% of 250 or 2.5 instances of
exceptions over the last year
 Too many exceptions indicate that
 either the model is understating VAR
 the Bank is unlucky
 How to decide ?
 Statistical inference
 On average, the number should be about 2.5
 Higher number could happen either because of Bad
Luck or because of a wrong risk model
 However, it is unlikely that this outcome is due solely
to bad luck

21. Visualizing VAR : Example
 A 1-day VAR of $10mm using a probability of 5%
means that there is a 5% chance that the
portfolio could lose more than $10mm in the next
trading day.
5%
1.645 Std Dev
Possible Profit/Loss
-10MM

22. Test of Frequency of Tail Losses or
Kupiec Test
 Kupiec’s (1995) test attempts to determine
whether the observed frequency of exceptions
is consistent with the frequency of expected
exceptions according to the VaR model and
chosen confidence interval. Under the null
hypothesis that the model is “correct”, the
number of exceptions follows a binomial
distribution.

23.  The probability 1 of experiencing x or more
exceptions if the model is correct is given by:
 Where x is the number of exceptions, p is the
probability of an exception for a given
confidence level, and n is the number of trials.

24.  If the estimated probability is above the
desired “null” significance level (usually 5% -
10%), we accept the model.
 If the estimated probability is below the
significance level, we reject the model and
conclude that it is not correct. We can conduct
this test for loss and gain exceptions to
determine how well the model predicts the
frequency of losses and gains beyond VaR
numbers.

25. Christoffersen’s
Independence Test
A likelihood ratio test that looks for unusually
frequent consecutive exceedances.
 However, it isn’t defined when there are no
consecutive exceedances at all.
 In some cases it may be reasonable to simply
accept the null hypothesis when there are no
consecutive exceedances. But, not always.
 For example, if you backtest a one-day 99% VaR
measure with 1,000 days of data, there should be
about 10 instances of consecutive exceedances.
If there are none, it might be inappropriate to
accept the null hypothesis.

26. Basel Committee “Traffic Light”
approach
Market-risk capital
multiplier, k is
suggested by the
Basel Committee in
the Capital Accord,
which is used to
compensate for the
possible
unreliability of the
bank’s VaR
calculator.
 The exceptions in 250 days is assumed to follow
a Bernoulli distribution

27. The need for VAR model
accuracy
 If the VAR is systematically “too low”, the model
is underestimating the risk and you tend to have
too many occasions where the loss in the
portfolio exceeds the VAR. This can lead to an
increase in the “multiplier” for the capital
calculation.
 If the VAR is systematically “too high”, the model
is over estimating the risk and your regulatory
capital charge will be too high

28. Obtaining Good Historical Data
 Poor Data
– Even actively traded markets can have “noisy” historical data
– Less actively traded markets can pose a significant challenge to
finding clean historical data
– Historical data can be misleading if a market is maturing over that
period
 Missing Data
– It may be difficult to find historical data in relatively new (e.g., U.K. Asset
Backeds) or inactive markets (e.g., inverse I.O.s)
 Asynchronous Data
– The data for risk factors that are traded against each other (e.g.,
Mortgages and
Treasuries, Futures and Cash Securities, etc.) must reflect simultaneous
closes.

29. Quantitative Standards
 Each bank must meet, on a daily basis, a capital requirement
expressed as the higher of
(i) its previous day’s value-at-risk number measured according to the
parameters specified in this section and
(ii) an average of the daily value-at-risk measures on each of the
preceding sixty business days, multiplied by a multiplication factor
 multiplication factor will be set by supervisory authorities on the basis of
their assessment of the quality of the banks risk management system,
subject to an absolute minimum of 3.
 Banks using models will also be subject to a capital charge to cover
specific risk (as defined under the standardised approach for market
risk) of interest rate related instruments and equity securities

30. Quantitative Standards
 “Value-at-risk”must be computed on a daily basis
 In calculating the value-at-risk, a 99th percentile, one-tailed confidence
interval is to be used
 “Holding period” will be ten trading days
 “Effective” historical observation period must be at least one year
 Banks should update their data sets no less frequently than once every three
months and should also reassess them whenever market prices are subject to
material changes
 No particular type of model is prescribed – should captures all the material
risks run by the bank