Introduction To Value At Risk

INTRODUCTION TO
VALUE AT RISK (VaR)

ALAN ANDERSON, Ph.D.
ECI Risk Training
www.ecirisktraining.com

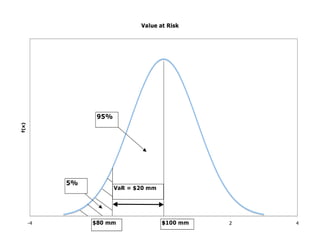
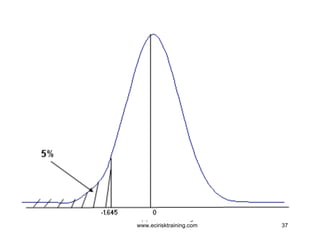
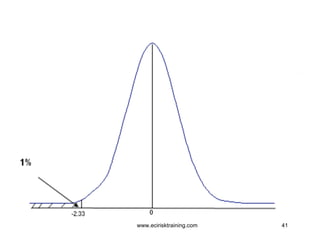
Value at Risk (VaR) is a statistical
technique designed to measure the
maximum loss that a portfolio of assets
could suffer over a given time horizon
with a specified level of confidence

(c) ECI Risk Training
www.ecirisktraining.com 2

Value at Risk was originally used to
measure market risk

It has since been extended to other
types of risk, such as credit risk and
operational risk


EXAMPLE

Suppose that it is determined that a
$100 million portfolio could potentially
lose $20 million (or more) once every
20 trading days


The VaR of this portfolio equals $20
million with a 95% level of confidence
over the coming trading day; 19 out of
20 trading days (95% of the time),
losses are less than $20 million


At the 95% confidence level, VaR represents
the border of the 5% “left tail” of the normal
distribution, also known as the fifth percentile
or .05 quantile of the normal distribution


This diagram shows that:

95% of the time, the portfolio’s
value remains above $80 million

5% of the time, the portfolio’s
value falls to $80 million or less

The VaR of this portfolio is therefore

$100 million - $80 million = $20 million


VaR is based on the assumption that the
rates of return of the assets held in a
portfolio are jointly normally distributed


VaR has the advantage that the risks
of different assets can be combined to
produce a single number that reflects
the risk of a portfolio


Further, the probability of a given
loss can be calculated using VaR

VaR can also be used to determine
the impact on risk of changes in a
portfolio’s composition


VaR has the disadvantage that it
is computationally intensive and
requires major adjustments for
non-linear assets, such as options


COMPUTING VaR

Value-at-Risk is based on the work of
Harry Markowitz, who was awarded
the Nobel Prize in Economics in 1990
for his pioneering research in the area
of portfolio theory


Portfolio theory shows how
risk can be reduced by holding
a well-diversified set of assets


A collection of assets is considered to be well-
diversified if the assets are affected differently
by changes in economic variables, such as
interest rates, exchange rates, etc.


As a result, a well-diversified portfolio is
less likely to experience extreme changes
in value; in this way, risk is reduced


In statistical terms, a well-diversified portfolio
contains assets whose rates of return have
very low or negative correlations with each
other


EXAMPLE

A portfolio consisting exclusively of oil
stocks would not be well-diversified, since
changes in the price of oil would have a
huge impact on the portfolio’s value


A portfolio invested in both oil stocks
and automotive stocks would be far
more diversified:


Rising oil prices would hurt the automotive
stocks while helping the oil stocks

Falling oil prices would hurt the oil stocks
while helping the automotive stocks


As a result, the impact of oil price
swings would be offset by changes in
the value of the automotive stocks

On balance, risk would be reduced


The risk of holding a portfolio containing two
assets, X and Y, is measured by its standard
deviation, as follows:


P = w
2
X
2
X +w 2
Y
2
Y + 2wX wY X Y


where:

P = the standard deviation
of the returns to the portfolio


X = standard deviation of
the returns to asset X

Y = standard deviation of
the returns to asset Y


wX = weight of asset X
wY = weight of asset Y

The weights represent the proportion
of the portfolio invested in each asset;
the sum of the weights is one


NOTE

If short-selling is not possible, then:

0 wX 1
0 wY 1

If short-selling is possible, the
weights can be negative

= “rho”

this represents the correlation
between the returns to assets
X and Y; -1 1


The lower is the correlation
between assets, the lower will
be the risk of the portfolio


The Value at Risk of a
portfolio is a function of:


the dollar value of the portfolio
the portfolio standard deviation
the confidence level
the time horizon


COMPUTING VaR FOR
A SINGLE ASSET

For a single asset, using daily
returns data at a confidence level
of c, the VaR is computed as:

V0

where:

V0 = initial value of the asset

= standard deviation of the
asset’s daily returns


= the number of standard deviations
below the mean corresponding to
the (1-c) quantile of the standard
normal distribution


EXAMPLE
For a 95% confidence level, c = 0.95

(1-c) is the fifth quantile (1-.95 = .05 =
5%) of the standard normal distribution

The corresponding value of is 1.645


The value of corresponding to any
confidence level can be found with a
normal table or with the Excel function
NORMSINV


EXAMPLE

For a 99% confidence level, the value
of can be determined as follows:


c = 0.99
(1-c) = 0.01 = 1%
NORMSINV(0.01) = -2.33
= 2.33


EXAMPLE

Suppose that an investor’s portfolio consists
entirely of $10,000 worth of IBM stock.

Since the portfolio only contains IBM stock,
it can be thought of as a single asset


Assume that the standard deviation of the
stock’s returns are 0.0189 (1.89%) per day


If the investor wants to know his
portfolio’s VaR over the coming
trading day at the 95% confidence
level, this would be calculated as
follows:


V0 = (10,000)(1.645)(0.0189)

= $310.905


This means that over the coming day,
there is a 5% chance that the investor’s
losses could reach $310.905 or more
(i.e., the portfolio’s value could fall to
$9,689.095 or less)


NOTE
VaR can be extended to different
time horizons by applying the square
root of time rule


According to this rule, the standard
deviation increases in proportion to
the square root of time:

t periods = t 1 period


If the investor wants to know his
portfolio’s VaR over the coming
month at the 95% confidence level,
based on the assumption that there
are 22 trading days in a month, this
would be calculated as follows:


V0 = (10, 000)(1.645)(0.0189 22)

(10, 000)(1.645)(0.0189 22) = $1, 458.27


Similarly, if the investor wants to know
what his portfolio’s VaR is over the coming
year, assuming that there are 252 trading
days in a year, the calculations would be:


V0 = (10, 000)(1.645)(0.0189 252)

(10, 000)(1.645)(0.0189 252) = $4,935.46


COMPUTING PORTFOLIO VaR

In order to compute the Value at
Risk of a portfolio of two or more
assets, the correlations among the
assets must be explicitly considered

The lower these correlations, the
lower will be the resulting VaR


The Value at Risk of a portfolio
is calculated by determining the:

weight (proportion of the total
invested) of each asset in the
portfolio


standard deviation of each asset’s
rate of return in the portfolio

correlations among the assets’ rates
of return in the portfolio


Once a confidence level and a time
horizon have been chosen, the
weights, volatilities and correlations
can be combined using Markowitz’s
approach to derive the portfolio’s VaR


EXAMPLE
Assume that a $100,000 portfolio
contains $60,000 worth of Stock X
and $40,000 worth of Stock Y.


Given the following data, compute
the VaR of this portfolio with a 95%
confidence level over the coming:


day
month
year


DATA
wX = 0.60 wY = 0.40
X = 0.016284 Y = 0.015380
= -0.19055


P = (0.6) (0.016284) + (0.4) (0.015380) +
2 2 2 2

2(0.6)(0.4)( 0.19055)(0.016284)(0.015380)

= 0.01144627 = 1.144627%


The portfolio VaR over the coming day is:

V0 P = (100,000)(1.645)(0.01144627)

= $1,882.91


The portfolio VaR over the coming month is:

V0 P = (100, 000)(1.645)(0.01144627 22)

= $8,831.638


The portfolio VaR over the coming year is:

V0 P = (100, 000)(1.645)(0.01144627 252)

= $29,890.29


Introduction To Value At Risk

More Related Content

What's hot

Similar to Introduction To Value At Risk

More from Alan Anderson

Recently uploaded

Introduction To Value At Risk