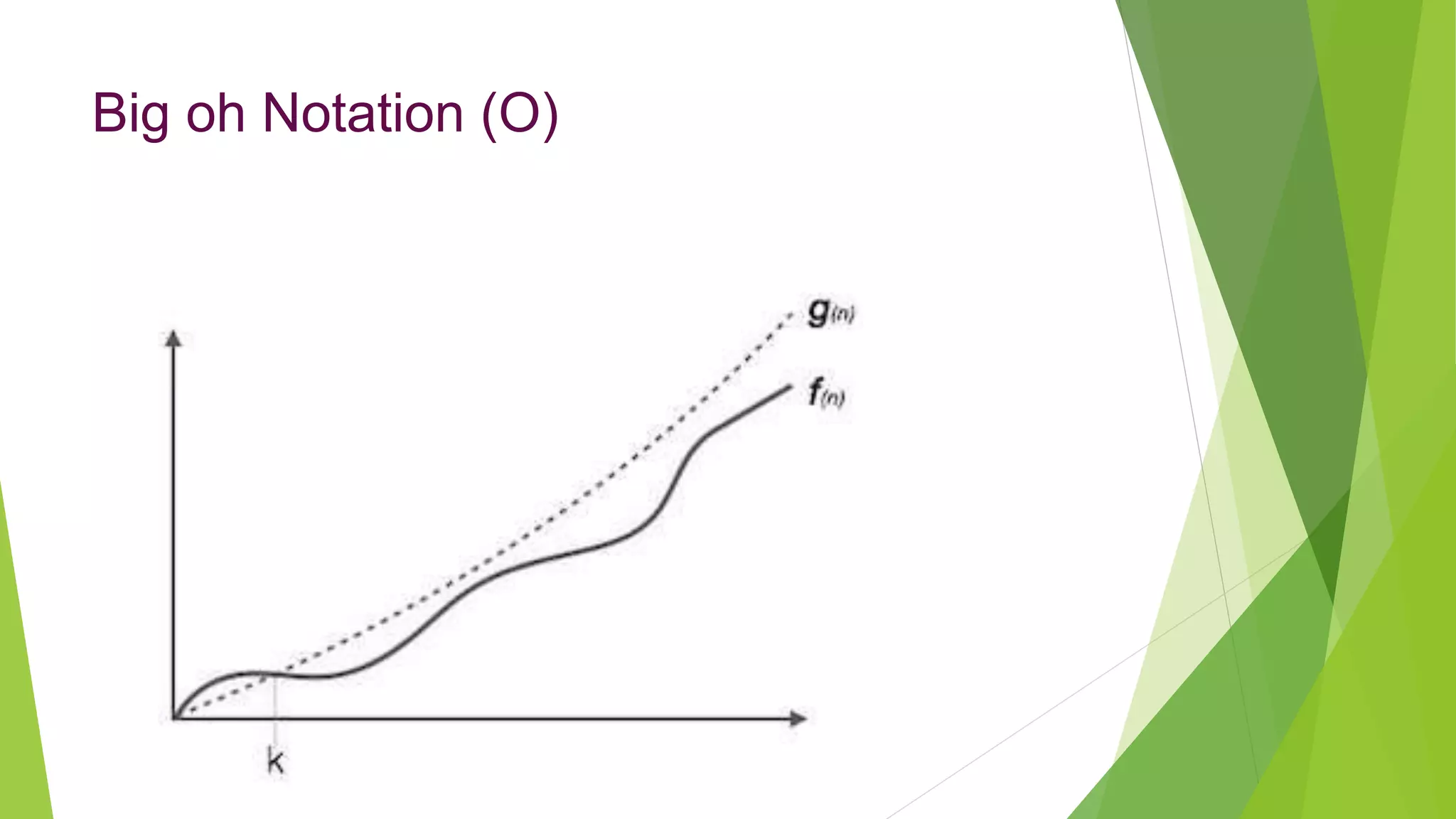
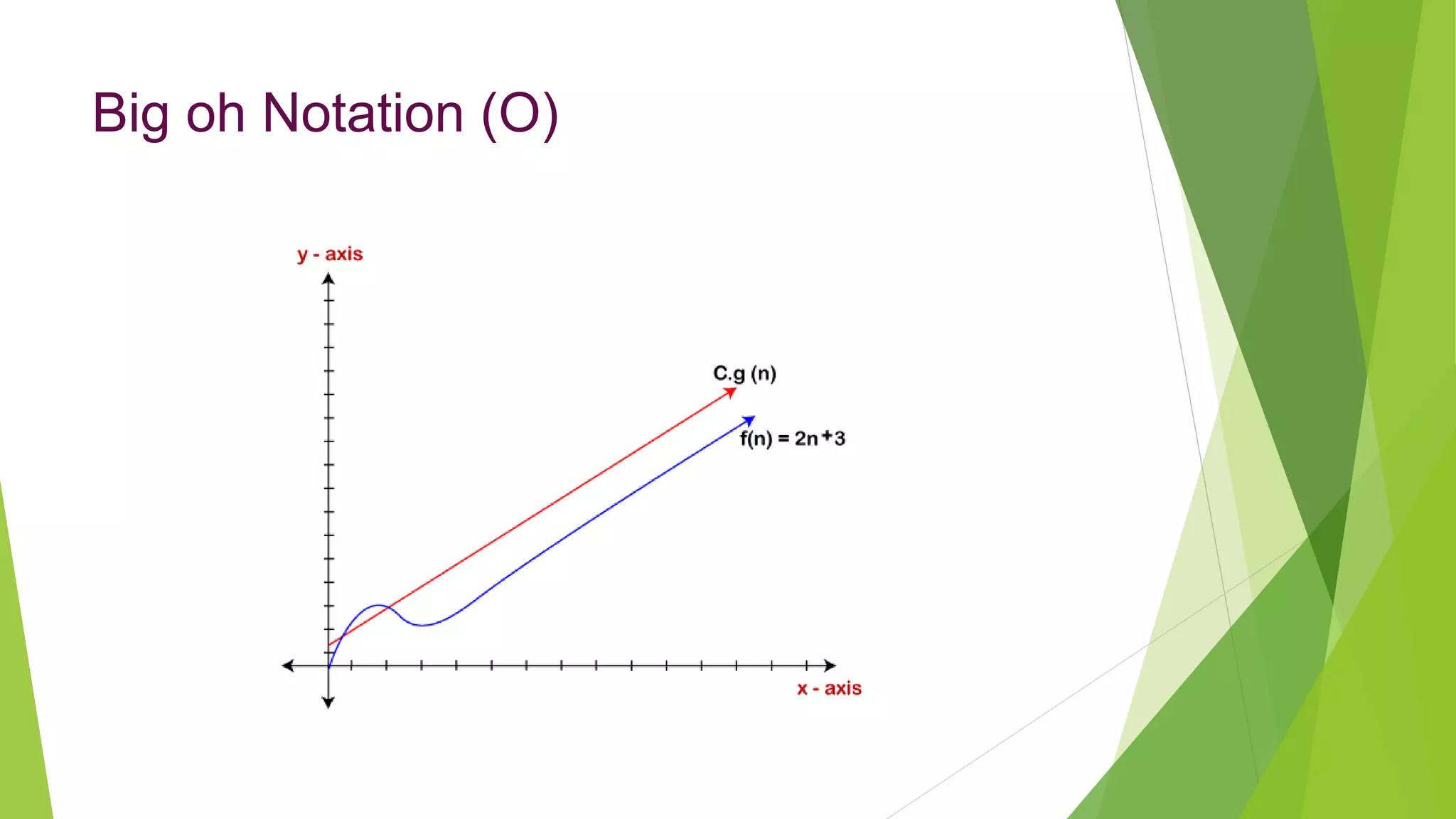
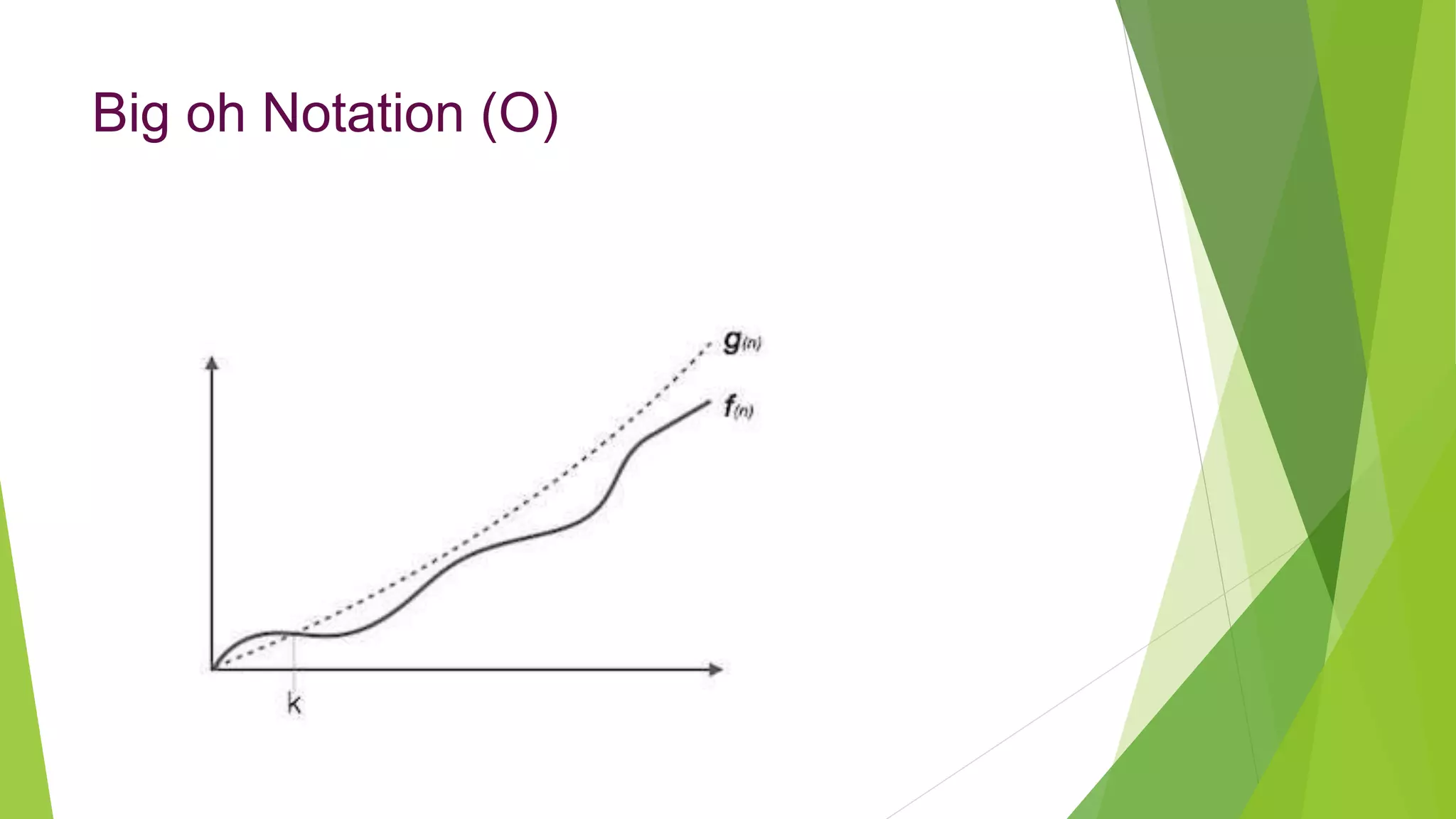
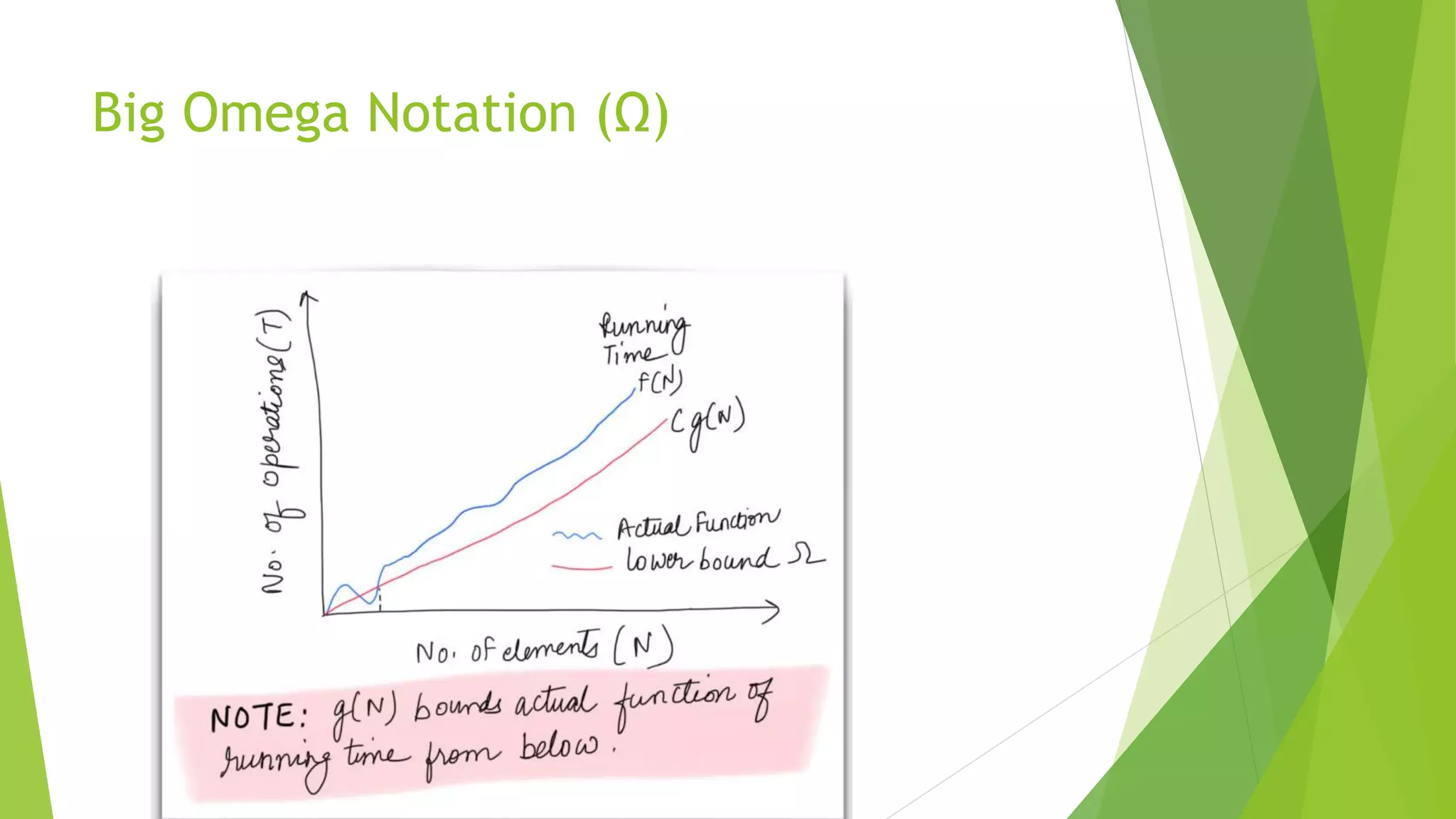
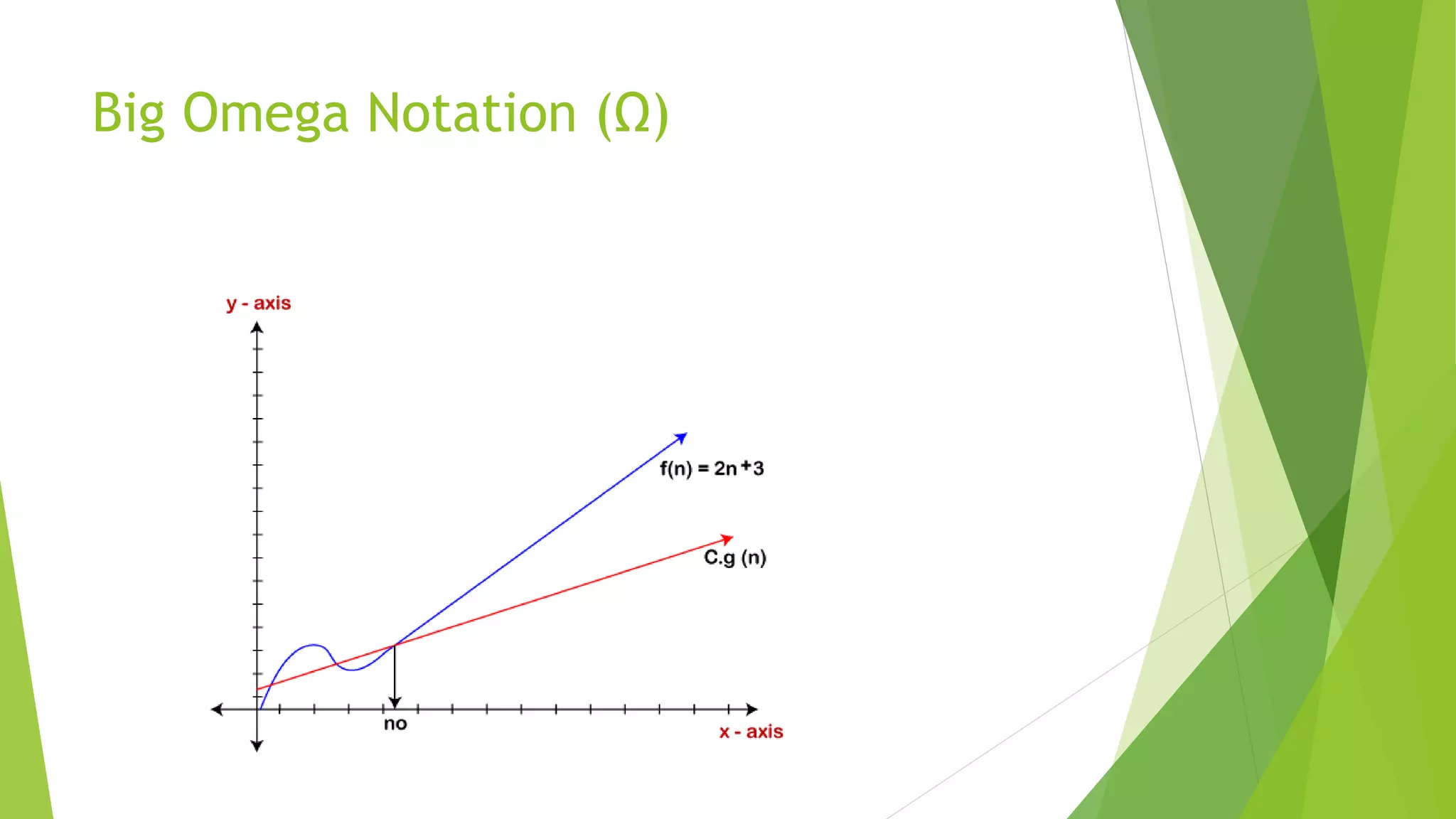
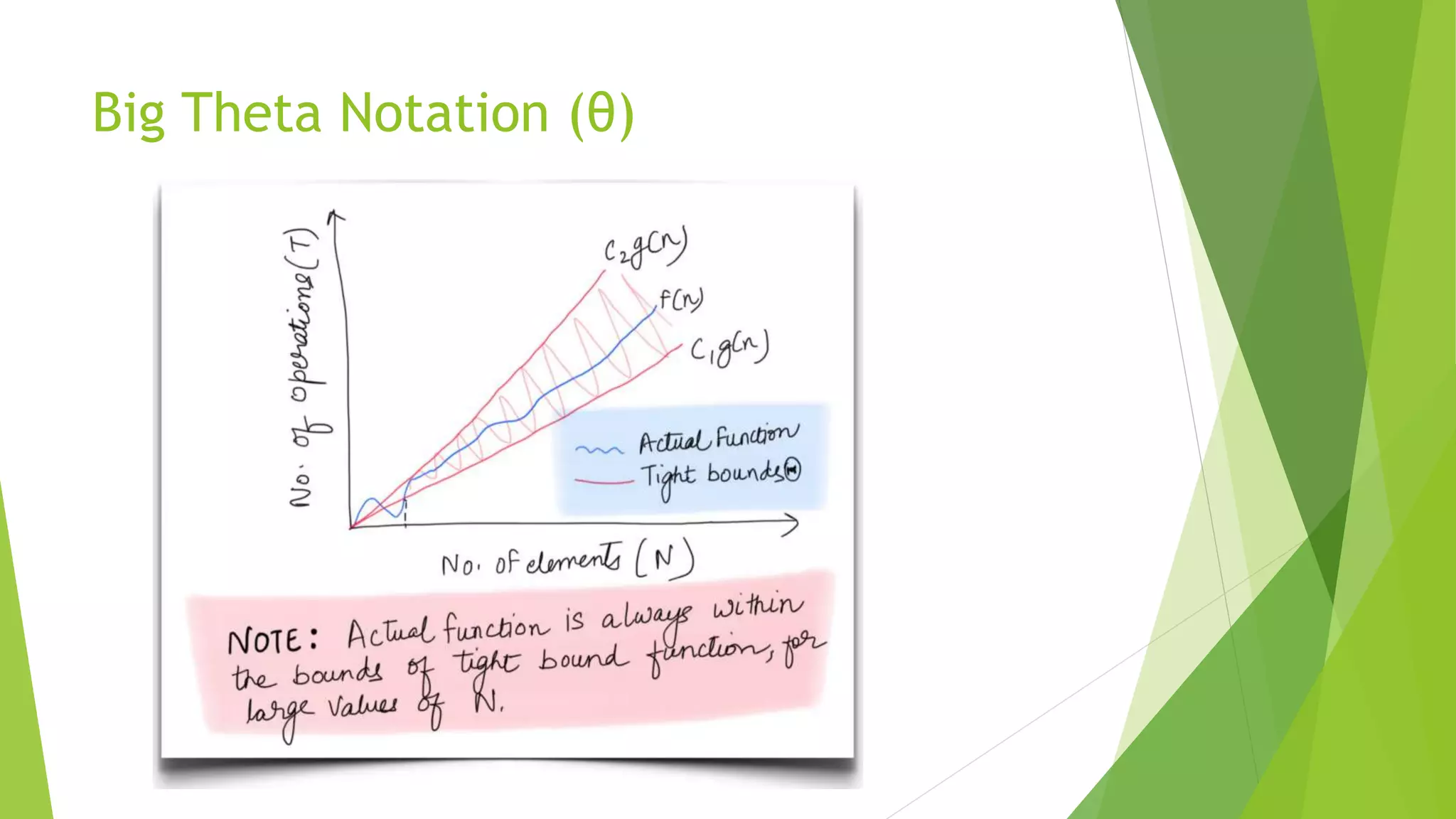
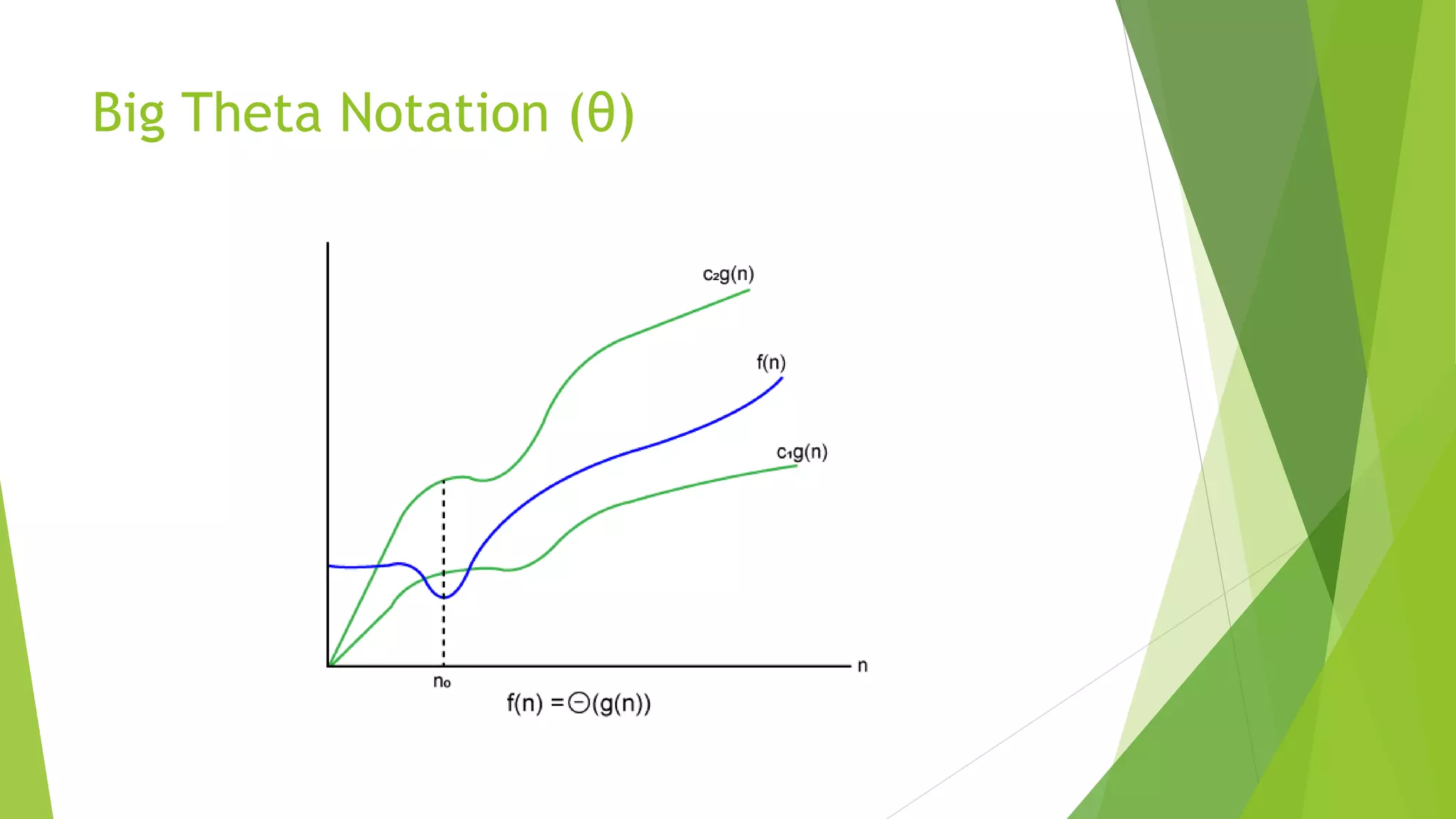
This document discusses asymptotic analysis and recurrence relations. It begins by introducing asymptotic notations like Big O, Omega, and Theta notation that are used to analyze algorithms. It then discusses recurrence relations, which express the running time of algorithms in terms of input size. The document provides examples of using recurrence relations to find the time complexity of algorithms like merge sort. It also discusses how to calculate time complexity functions like f(n) asymptotically rather than calculating exact running times. The goal of this analysis is to understand how algorithm running times scale with input size.