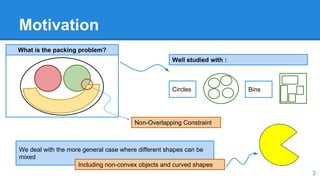
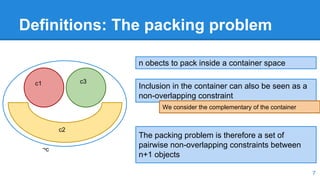
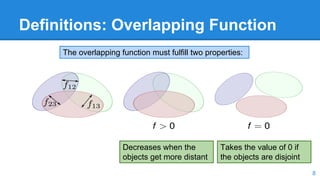
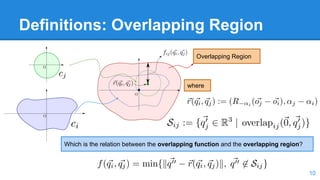
This document presents a method for packing curved and non-convex objects without overlap. The method uses an offline algorithm to calculate the overlapping region between all object pairs and the minimum distance between them. An online inner inflation method then finds the closest non-overlapping configuration by iteratively inflating objects within their overlapping regions. Experimental results show the approach can pack arbitrary object shapes, including rotations, but has increasing processing time with more complex object combinations.

1. Packing Curved
Objects
Ignacio SALAS & Gilles CHABERT

2. Outline
Motivation
Method
Method: Inner Inflator
Experimental Results
Conclusions
Definitions
2

3. Motivation
3
What is the packing problem?
Well studied with :
Circles Bins
We deal with the more general case where different shapes can be
mixed
Including non-convex objects and curved shapes
Non-Overlapping Constraint

4. Motivation: Using CMA-ES
In [Mar13] the packing problem was solved minimizing a violation function
with the CMA-ES algorithm. The function is a measure of overlapping.
The approach gives
encouraging results, but
requires ad-hoc distance
functions for each pair of
objects
Our objective is to replace these ad-hoc formulas by a numerical algorithm
4

5. Definitions: The objects
We consider objects described by nonlinear inequalities,
with and/or operators in the shape description
5

6. Definitions: The non-overlapping
constraint
The non-overlapping constraint is the negation of
the latter relation
6
qi
and qj
are parameters of Objects n°i and j
Rotation Translation

7. Definitions: The packing problem
The packing problem is therefore a set of
pairwise non-overlapping constraints between
n+1 objects
n obects to pack inside a container space
Inclusion in the container can also be seen as a
non-overlapping constraint
We consider the complementary of the container
c1
c2
c3
¬c
7

8. Definitions: Overlapping Function
The overlapping function must fulfill two properties:
8
Decreases when the
objects get more distant
Takes the value of 0 if
the objects are disjoint

9. Definitions: Overlapping Function
A ｟distance to satisfaction｠
A generic definition is:
9

10. Definitions: Overlapping Region
Overlapping Region
10
where
Which is the relation between the overlapping function and the overlapping region?

11. Off-line
Method
Calculate the
Overlapping Region Sij
Calculate the
minimal distance
between r(qi, qj)
and Sij
Paving
Algorithm
Paving of the Overlapping Region
Distance
calculation
qi
qj
11
Object i
Object j

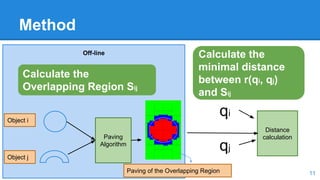
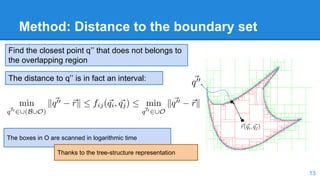
12. Method: Paving of the Overlapping Region
Outer Rejection Test
Inner Inflation [detailed further]
Bisection
Branch and Bound algorithm, that alternates 3 steps:
Starts with an arbitrary large box [qj]
The paving is stored in a tree structure
12

13. Method: Distance to the boundary set
Find the closest point q’’ that does not belongs to
the overlapping region
The distance to q’’ is in fact an interval:
The boxes in O are scanned in logarithmic time
Thanks to the tree-structure representation
13

14. Resulting
inflation
Method: Inner Inflation
p satisfies
14
Translation Rotation
The boundary angles of [ᾱ , ⍶] are two angles that
makes the boundary of Object j meets p
~
~

15. Method: Inner Inflation
15
Cartesian
Product [ᾱ , ⍶][oj
]

16. Experimental Results
16
Off-line
On-line
5 experimental
cases
Circle Packing
Ellipse Packing
Ellipse Packing +
rotation
Horseshoes
Packing
Mixed Packing
Case 4
Case 5
1
2
3
4
5

17. Conclusions
We have presented a numerical algorithm that replaces such formulas.
The experimental results shows that our approach:
In [Mar13] was proposed an original approach for solving the generic packing
problem, requiring ad-hoc distance formulas.
17
Is not competitive for standard packing problems.
But is able to pack arbitrary objects, including non-convex ones.
The approach is particularly well-suited for uniform packing.
Limitation: the processing time increases with the number of shapes.
Objects with the same shape

18. Thank You !
18

19. Packing Curved
Objects
Ignacio SALAS & Gilles CHABERT