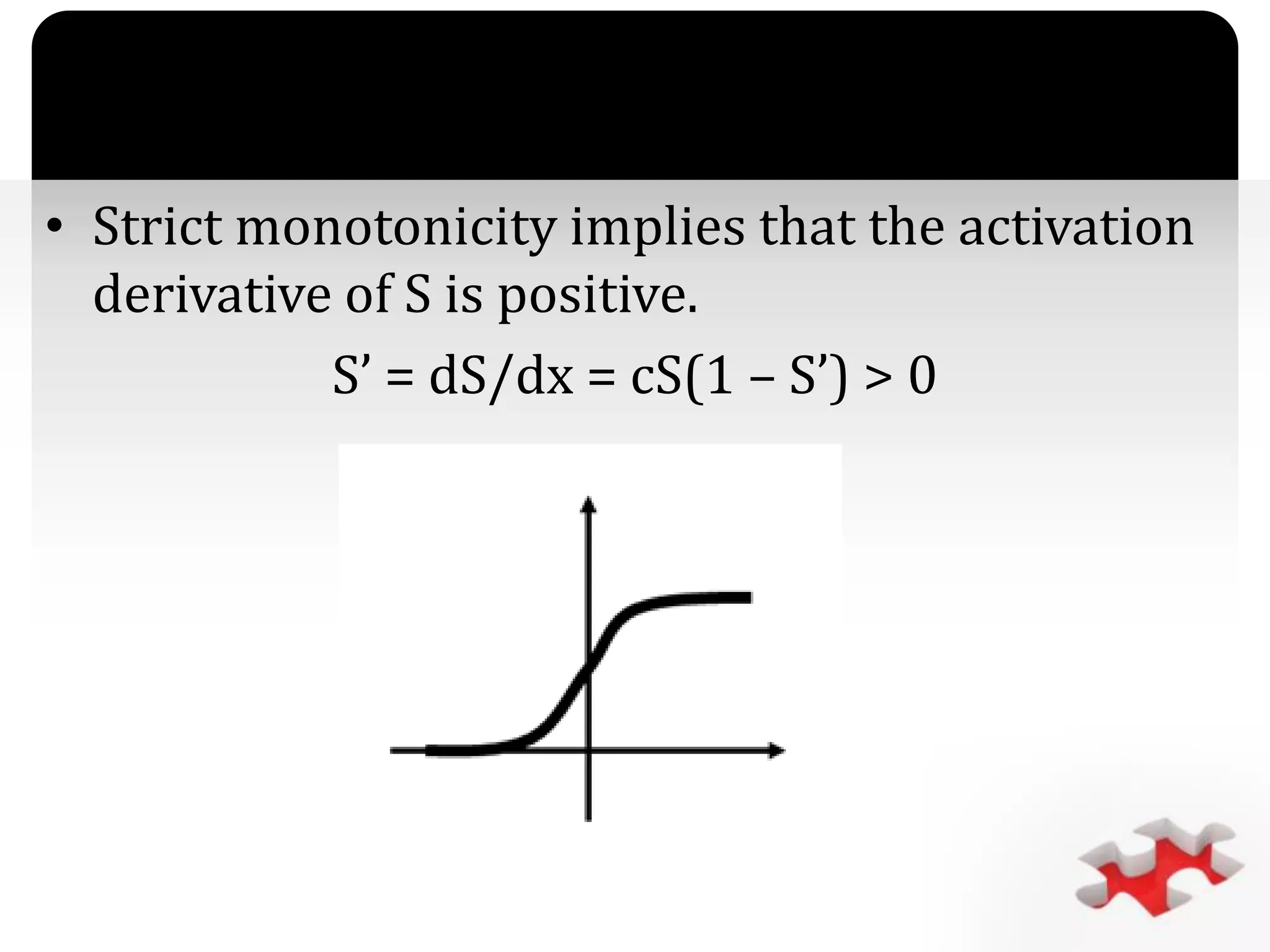
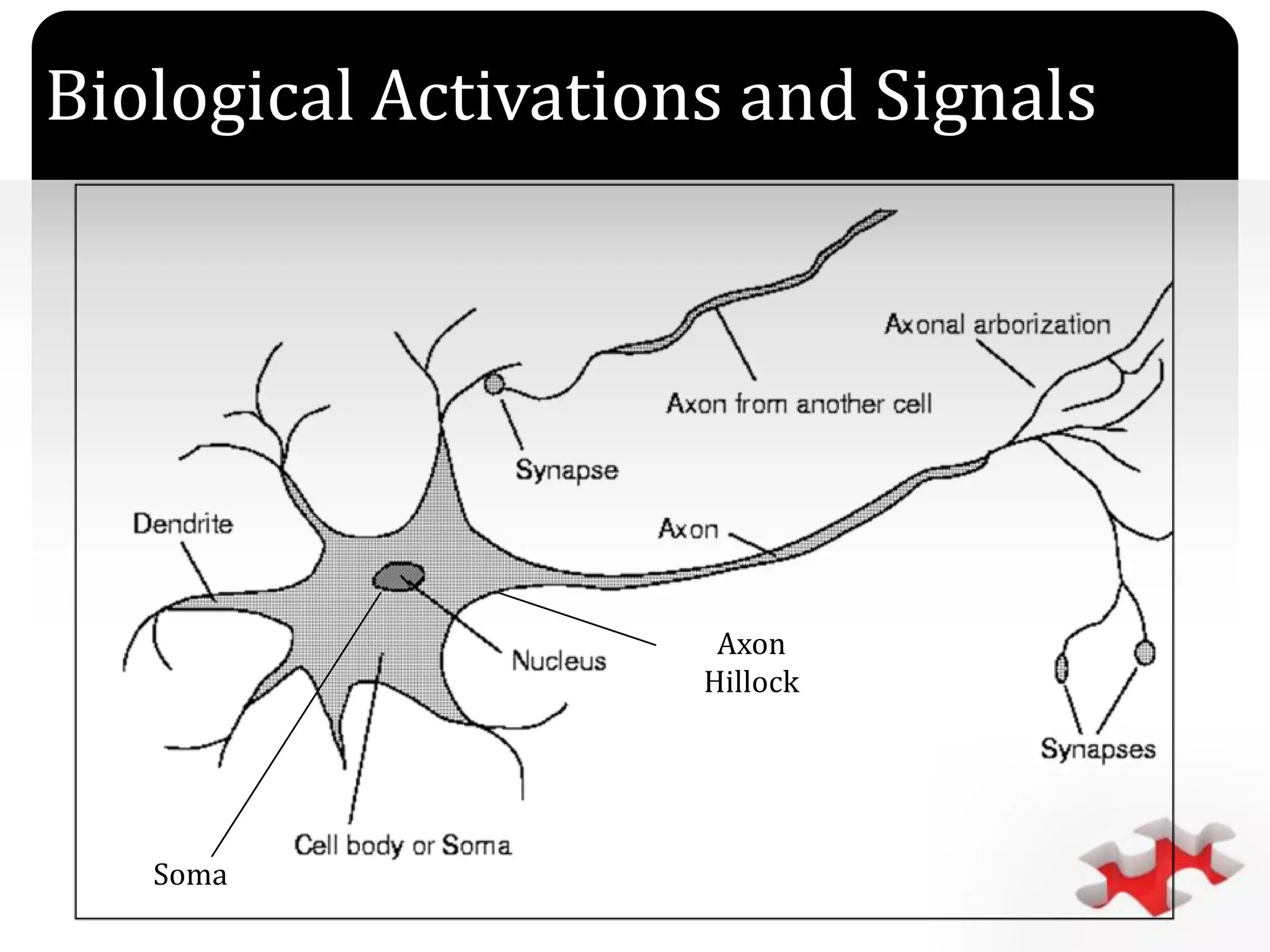
The document discusses artificial neural networks (ANNs) as mathematical models emulating biological neural systems, highlighting their utility in data mining and decision-support applications. It explains key concepts such as neuron functions, signal monotonicity, and the structure of neural networks, including components like soma, dendrites, axons, and synapses. Additionally, it outlines neuronal dynamic systems governed by differential equations, illustrating their time evolution and interconnectivity.

1. ARTIFICIAL INTELLIGENCE
Bharat P. Patil
M.Sc. C.S. Part II
64
Neural Network Theory

2. `
Neural Network
• An artificial neural network (ANN), often
just called a "neural network" (NN), is a
mathematical model or computational
model based on biological neural networks,
in other words, is an emulation of biological
neural system.

3. `
Why Neural Network?
• Neural networks are useful for data mining and
decision-support applications.
• People are good at generalizing from experience.
• Computers excel at following explicit instructions
over and over.
• Neural networks bridge this gap by modeling, on
a computer, the neural behavior of human brains.

4. `
NEURONS AS FUNCTIONS
• Neurons transforms an activation x(t) into a
bounded output signal S(x(t)).
• Usually a sigmoid function is used for this
purpose.
• A sigmoidal curve also describes the input-output
behavior of many operational amplifier.
• For instance, the logistic signal function,
S (x) = 1/1+ e-cx
is sigmoidal and strictly increases for positive
scaling constant c > 0.

5. `
• Strict monotonicity implies that the activation
derivative of S is positive.
S’ = dS/dx = cS(1 – S’) > 0

6. `
• The threshold signal function illustrates a non-
differentiable signal function. In general signal
function are piece wise differentiable.
• The family of logistics signal functions, indexed
by c, approaches asymptotically the threshold
function as c increases to positive infinity.
• Then S transduces positive activation x to unity
signals, negative activations to zero signals.
• We can arbitrarily transduce zero activation to
unity, zero, or the previous signal value.

7. `
Signal Monotonicity
• Signal functions are monotone non-decreasing
S’ ≥ 0.
• Increasing activation values can only increase the
output signal or leave it unchanged. They can
never decrease the signal.
• One admissible possibility, often found in
simulation discretization, is an increasing
staircase signal function.
• The staircase signal function is a piece wise
differentiable monotone non-decreasing signal
function.

8. `
• Gaussian signal function represents an important
exception to signal monotonicity.
• Gaussian signal function take the form S(x) =
for c > 0.
• Then S’ = -2cx .
• So the sign of signal activation derivative S’ is
opposite the sign of activation X.
• Generalized Gaussian signal function define
potential or radial basis functions
Si(x) = exp -

9. `
• For input activation vector x = (x1,…….,xn) ϵ , Rn
variance ,and mean vector
• Each radial basis function defines a spherical
respective field in Rn.
• The ith neuron emits unity, or near-
unity, signals for sample activations vectors x
that fall in its respective field.
• The radius of the Gaussian spherical receptive
field shrinks as the variance decreases.

10. `
Soma
Biological Activations and Signals
Axon
Hillock

11. `
Terminologies
• Soma: A neuron is composed of nucleus and the
cell body is termed as Soma.
• Dendrite: This is attached to the Soma which are
long irregular shaped elements. They behave a s
an input channel that is all the input from the
other neuron arrive through the dendrite.
• Axon: Another type of link attached to the soma is
the axon. Unlike the dendrite links the Axon are
electrically active and serve as a output channel.

12. `
The Axon mainly appears on the output cell which
are non-linear threshold devices producing a
voltage pulse called the Action Potential or the
Spike.
The neuron fires by propagating the Action
Potential down the Axon to exhit or inhibit the
other neurons.
• Synapse: The Axon terminates in a specialized
contact called synapse or synaptic junction that
connects the Axon with the dendritic link of the
other neuron. This junction is responsible for
accelerating or retarding the electrical charges to
the Soma.

13. `
• Axon Hillock: Membrane potential differences
or pulses accumulate at the membrane of the
Axon Hillock, where the neuron connects to
one of its axons or long branches.
• Synaptic Junction: The large signal pulse
propagates down the Axon and its branches,
where axonal insulators restore and amplify
the signal as it propagates until it arrives at a
Synaptic junction.

14. `
Neuron Fields
• A field of neurons is a topological grouping.
• Neural networks contain many fields of
neurons.
• Neurons within the field are topologically
ordered, often by proximity.
• Planar hexagonal packing of neurons provides
a different topological ordering.
• Three dimensional or volume proximity
packing, often found in mammalian
brains, provides another topological ordering.

15. `
• We assume that neurons are not topologically
ordered . They are related by synaptic
connection between them.
• Kohonen calls this lack of topological structure
in a field of neurons the zeroth order
topology.
• Fx = default field of neurons.
• Fy = second field of neuron.
• Fz = third field of neuron.

16. `
• We use minimal neural hierarchies {Fx, Fy} or
{Fx, Fy, Fz}. Instead of more accurate, more
cumbersome index hierarchy notation
{F1…….Fk}.
• We denote a three layer feed forward neural
network as Fx  Fy  Fz.
• Fx = Input fields.
• Fz = Output fields.

17. `
Neuronal Dynamic System
• Neuronal Dynamic System is described by a
system of first order differential or difference
equation that governs the time evolution of
neuronal activation or membrane potentials.
• For fields Fx and Fy.
x1 = g1 (Fx, Fy,…)
.
.
xn = gn (Fx, Fy,…)

18. `
y1 = h1 (Fx, Fy,…)
.
.
yn = hn (Fx, Fy,…)
In vector notation,
x = g (Fx, Fy,…)
y = h (Fx, Fy,…)

19. `
• Where xi and yj denote the activation time
function of the ith neuron in Fx and the jth
neuron in Fy. The arguments of gi and hj
functions also include synaptic and input
information.
• We do not include time as an independent
variable. As a result, in dynamical system
theory, neural-network models classify as
autonomous dynamical system.

20. `