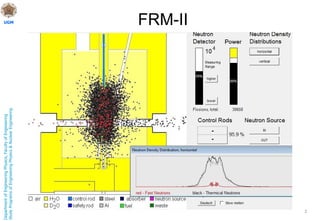
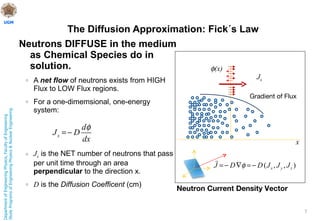
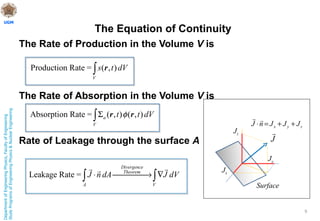
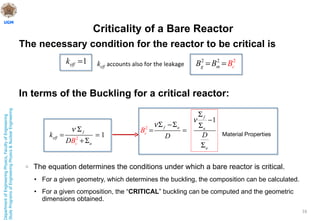
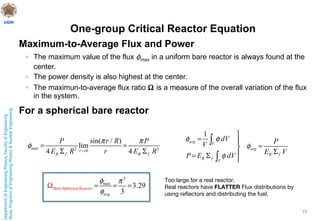
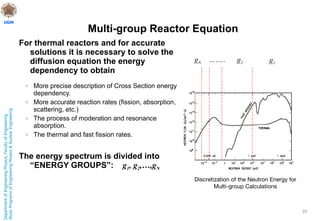
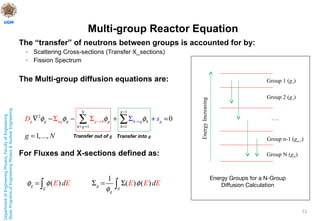
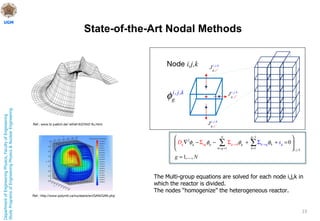
This document discusses nuclear reactor theory and modeling approaches. It introduces the neutron flux as the main variable and describes how it is necessary to approximate the behavior of neutrons using methods like Monte Carlo, analytic transport, and diffusion approximations. It then discusses the diffusion approximation and equation in more detail, including the concept of neutron diffusion and boundary conditions. Finally, it discusses moving to multi-group and state-of-the-art nodal methods to more accurately model the energy dependence and heterogeneity in reactors.

1. Nuclear Reactor Theory - Nuclear Reactor Analysis -

2. FRM-II

3. The Neutron Flux The Neutron Flux is the Main Variable in Nuclear Reactor Theory To design and analyze a nuclear reactor it is necessary to predict: How the neutrons are spatially distributed. How the neutron population evolves with time. An exact calculation would need to track the neutrons as they move in the system. This is not possible with current computer capabilities We need to use Approximations: Monte Carlo Methods. Analytic Neutron Transport Methods. Neutron Diffusion Approximation.

4. The Neutron Flux In a reactor neutrons have many different energies: The neutrons move with velocities The neutrons interact with a probability per unit length The reaction rate can be written as The neutron FLUX is

5. The Neutron Flux Typical Neutron Energy Spectrum Ref.: http://www.tpub.com/content/doe/h1019v1/css/h1019v1_138.htm

6. FRM-II

7. The Diffusion Approximation: Fick´s Law Neutrons DIFFUSE in the medium as Chemical Species do in solution. A net flow of neutrons exists from HIGH Flux to LOW Flux regions. For a one-dimemsional, one-energy system: J x is the NET number of neutrons that pass per unit time through an area perpendicular to the direction x. D is the Diffusion Coefficent (cm) Neutron Current Density Vector x  (x) J x Gradient of Flux

8. The Equation of Continuity It is the conservation equation of neutrons in a medium The Total number of neutrons in a Volume V is The Rate of Change is: V r

9. The Equation of Continuity The Rate of Production in the Volume V is The Rate of Absorption in the Volume V is Rate of Leakage through the surface A Surface J x J z J y

10. The Diffusion Equation The Continuity Equation The Diffusion Eq . Fick´s Law Diffusion Length The integrands must satisfy The integration is over the same volume V

11. The Diffusion Equation Boundary Conditions The neutron flux can be found by solving the diffusion equation. It requires the specification of BOUNDARY conditions for the FLUX. Physical: The flux must be always POSITIVE. The flux must be FINITE. Geometry: Vacuum Boundary Condition: Unreflected Core Interface Boundary Conditions for two adjacent regions A B n d  x)  d)=0

12. The Diffusion Equation The Diffusion Variables Validity of the Fick´s Law Approximation: Fick´s Law IS NOT an exact relation, but an approximation. It is not valid: In a medium that strongly absorbs neutrons (e.g. near control rods). Within about three mean free paths of either a neutron source or the surface of a medium. For strongly anisotropic neutron scattering. Low A High A Reflectors have LOW A

13. One-group Reactor Equation The design of a reactor requires The calculations of the conditions necessary for criticality. The calculation of the distribution of neutrons to determine the power distribution in the system: Establish the thermal conditions. Determine the needs for heat removal during operation and abnormal conditions. The simplest equation is for a “bare” Fast Reactor One-group Flux and Neutronic Parameters One-group Reactor Equation:

14. One-group Reactor Equation The source of neutrons In a steady state reactor the source of neutrons is mainly the fissions in the fuel. The average number of neutrons per fission is The source can be expressed in terms of the rate of absorptions as And in Terms of k ∞

15. One-group Reactor Equation In Steady-state, if the fission source does not balance the Leakage and the absorption, the equation is not satisfied. The source term is multiplied by 1/k eff . The Buckling is defined as And the k eff is Material Buckling Geometric Buckling

16. Criticality of a Bare Reactor The necessary condition for the reactor to be critical is In terms of the Buckling for a critical reactor: The equation determines the conditions under which a bare reactor is critical. For a given geometry, which determines the buckling, the composition can be calculated. For a given composition, the “ CRITICAL ” buckling can be computed and the geometric dimensions obtained. k eff accounts also for the leakage Material Properties

17. One-group Critical Reactor Equation Examples of Solutions Power Energy per fission The Solution for the Flux is: Buckling Spherical Critical Reactor The flux is a function only of the radius r Homogeneous Reactor The power is given by the integral There are many possible values of B that will satisfy the boundary conditions , but the geometrical buckling is the FIRST eigenvalue B 1 r R

18. One-group Critical Reactor Equation Examples of Solutions Finite Cylindrical Critical Reactor The flux is a function of the radius r and z Two Functions: The solution: Homogeneous Reactor z r H/2 H/2 R

19. One-group Critical Reactor Equation Maximum-to-Average Flux and Power The maximum value of the flux  max in a uniform bare reactor is always found at the center. The power density is also highest at the center. The maximun-to-average flux ratio  is a measure of the overall variation of the flux in the system. For a spherical bare reactor Too large for a real reactor. Real reactors have FLATTER Flux distributions by using reflectors and distributing the fuel.

20. Multi-group Reactor Equation For thermal reactors and for accurate solutions it is necessary to solve the diffusion equation the energy dependency to obtain More precise description of Cross Section energy dependency. More accurate reaction rates (fission, absorption, scattering, etc.) The process of moderation and resonance absorption. The thermal and fast fission rates. The energy spectrum is divided into “ENERGY GROUPS”: g 1 , g 2 ,…,g N g 1 g 2 g N …… .. Discretization of the Neutron Energy for Multi-group Calculations

21. Multi-group Reactor Equation The “transfer” of neutrons between groups is accounted for by: Scattering Cross-sections (Transfer X_sections) Fission Spectrum The Multi-group diffusion equations are: For Fluxes and X-sections defined as: Group 1 ( g 1 ) Group 2 ( g 1 ) Group n-1 ( g n-1 ) Group N ( g N ) … . Energy Increasing Energy Groups for a N-Group Diffusion Calculation Transfer out of g Transfer into g

22. Multigroup Diffusion Core Analysis Codes Modern Core Analysis Codes They use the Multi-group Diffusion Equations in two or several groups Two to six Groups: Fast and Thermal + additional resonance region groups. Cross sections are obtained form Advanced Transport based Lattice-Codes (e.g. CASMO-4, WIMS, NEWT): Energy Averages maintaining Reaction Rates. Spatial-Material Averages: Heterogeneous Cores. Corrections to the Diffusion Approximation: Neutronic Information from Lattice-Codes with Neutron Transport Corrections. Advanced formulations of NET NEUTRON CURRENTS across interfaces and in highly absorbing regions. Algorithms to “reconstruct” the local flux at the fuel rod level. Examples: SIMULATE, DIF3D, PARCS.

23. State-of-the-Art Nodal Methods Ref.: www.fz-juelich.de/ ief/ief-6/2/htr2-flu.html Node i,j,k Ref.: http://www.polymtl.ca/nucleaire/en/GAN/GAN.php The Multi-group equations are solved for each node i,j,k in which the reactor is divided. The nodes “homogenize” the heterogeneous reactor.

24. Neutron Transport Transport theory is based on the Boltzmann Equation developed for the kinetic theory of gases. The development of nuclear reactors in the 1940 applied the equation to the transport of neutrons in Reactor design and Radiation shielding. Analytical solutions are very difficult for real 3D-configurations. Today, the Transport Equation is solved numerically by discretizing the Angular, Energy, and Time Dependence of the neutron flux and the cross sections. It is a more accurate description of the neutron field than the diffusion equation.

25. Neutron Transport Neutron Transport Methods account for the angular direction Fission Source Scattering External Neutron Source Time variation and removal of neutrons Angular Flux and Neutron Density z x y dV dA