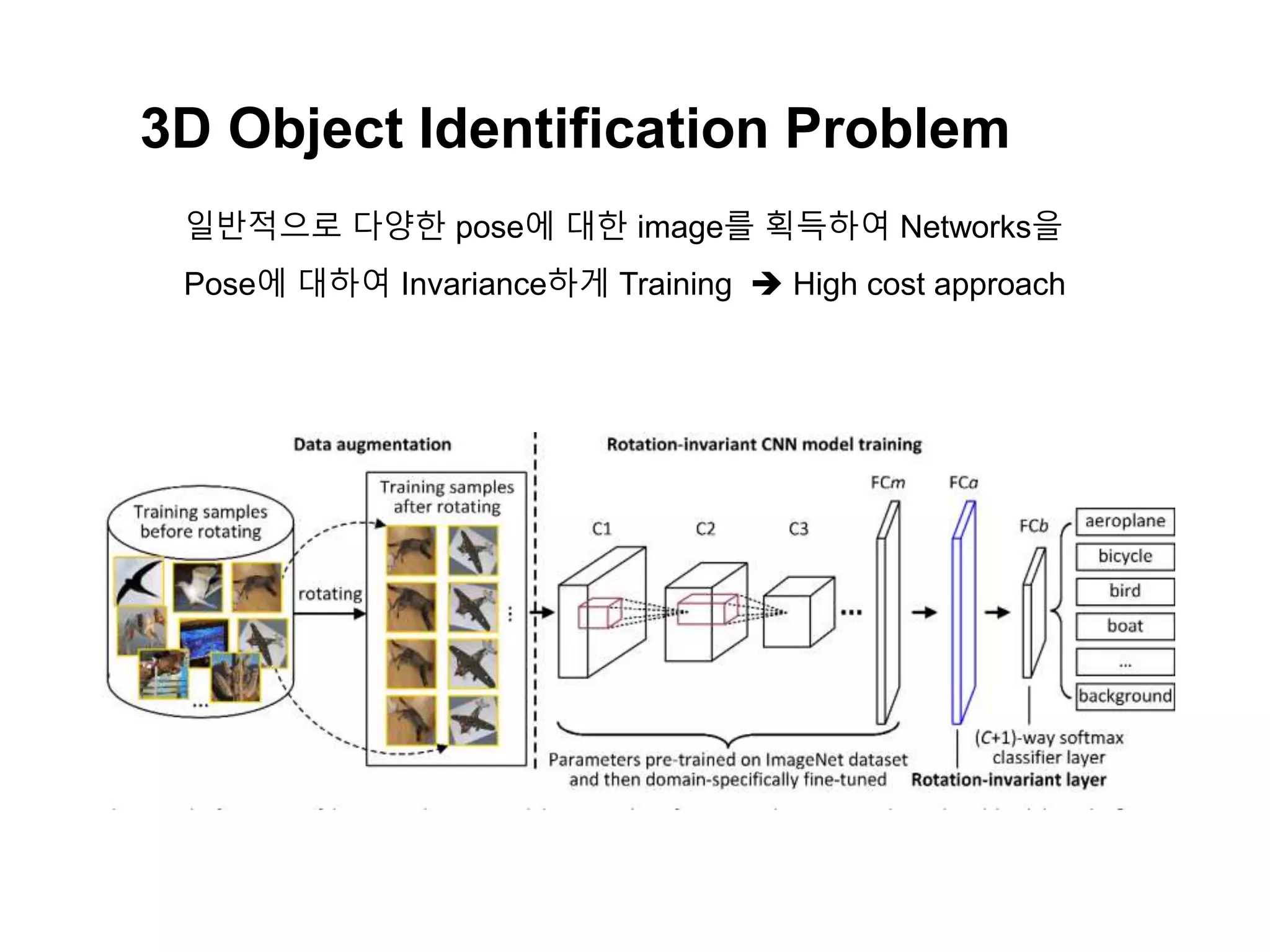
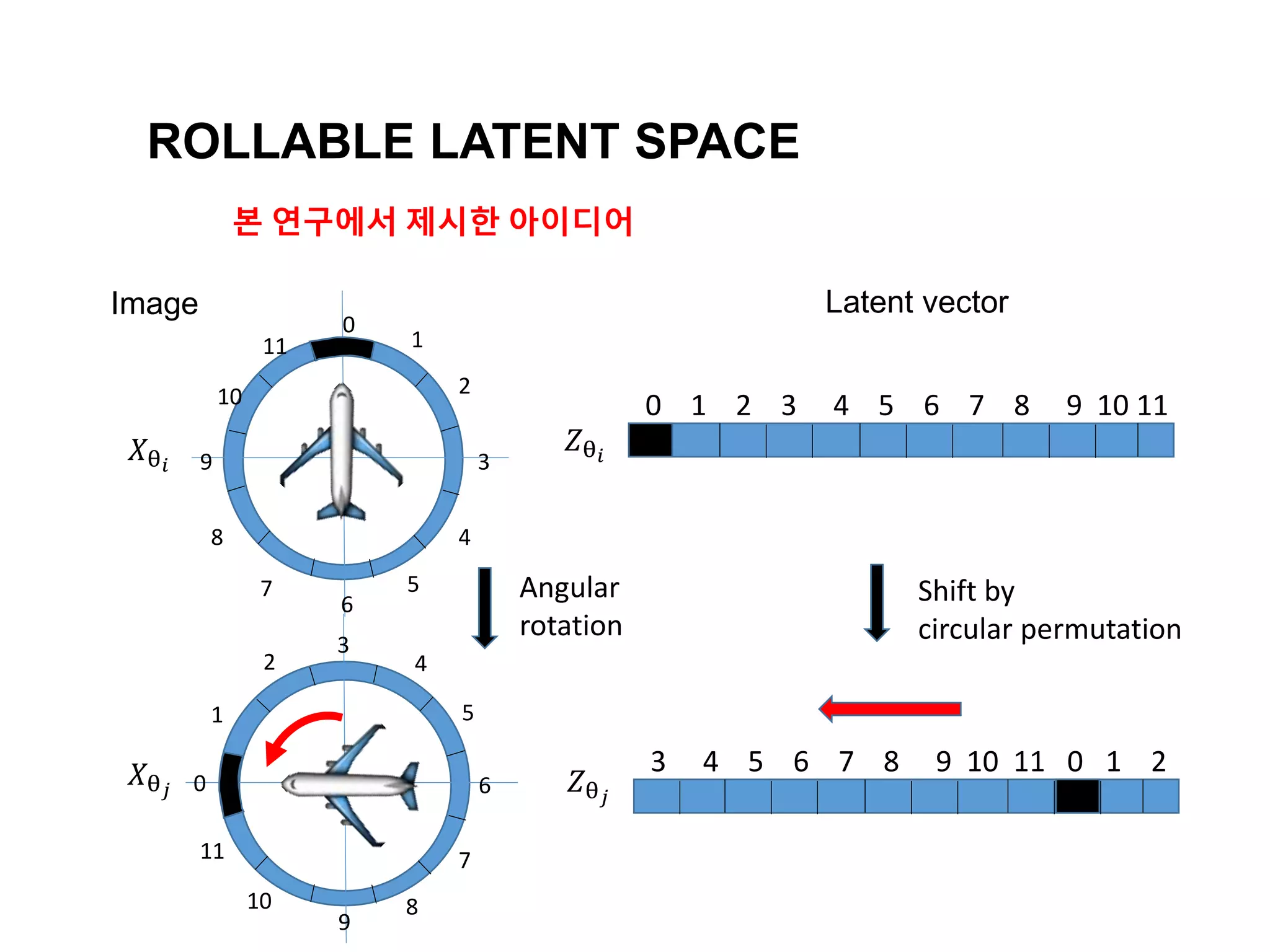
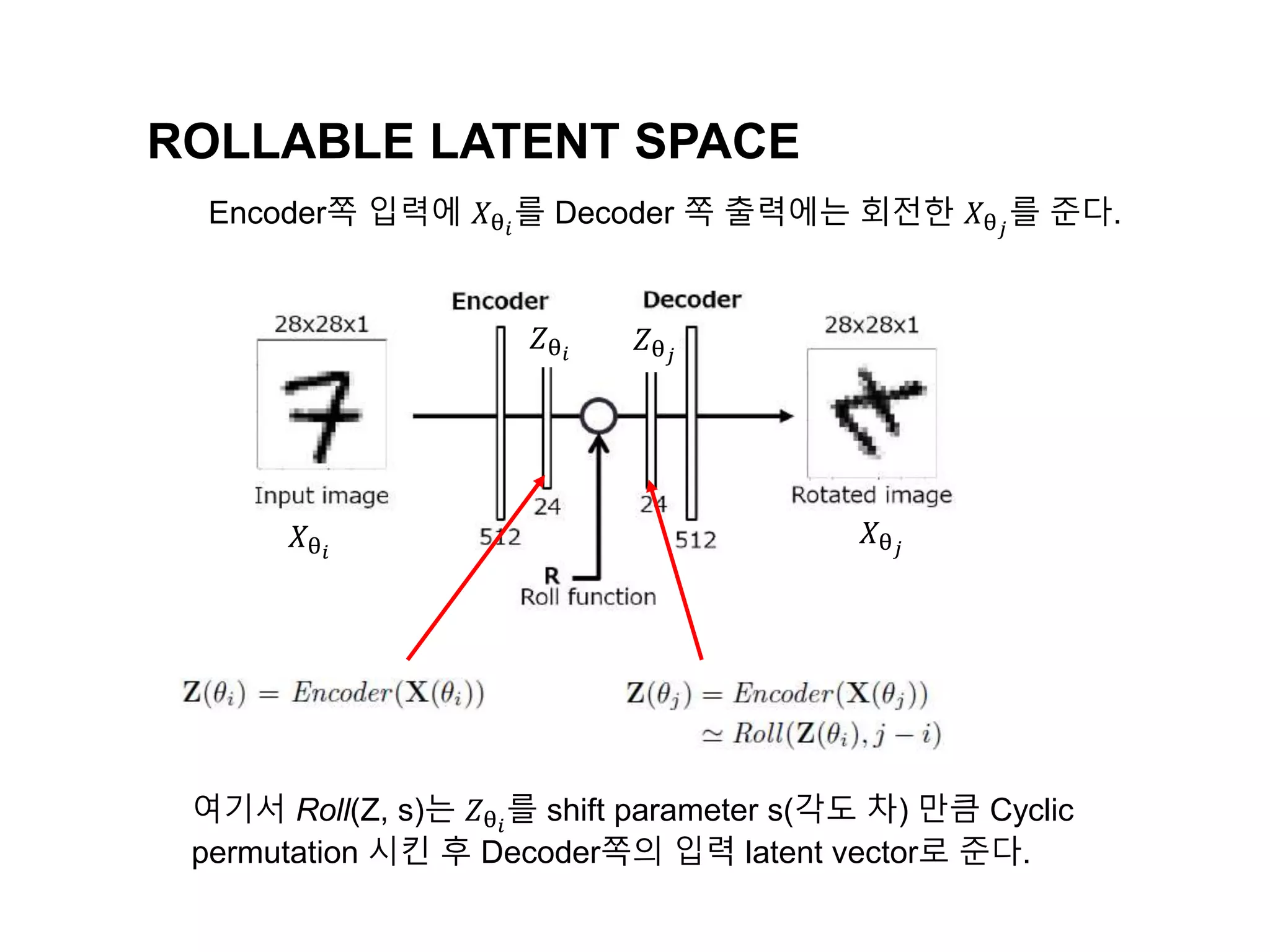
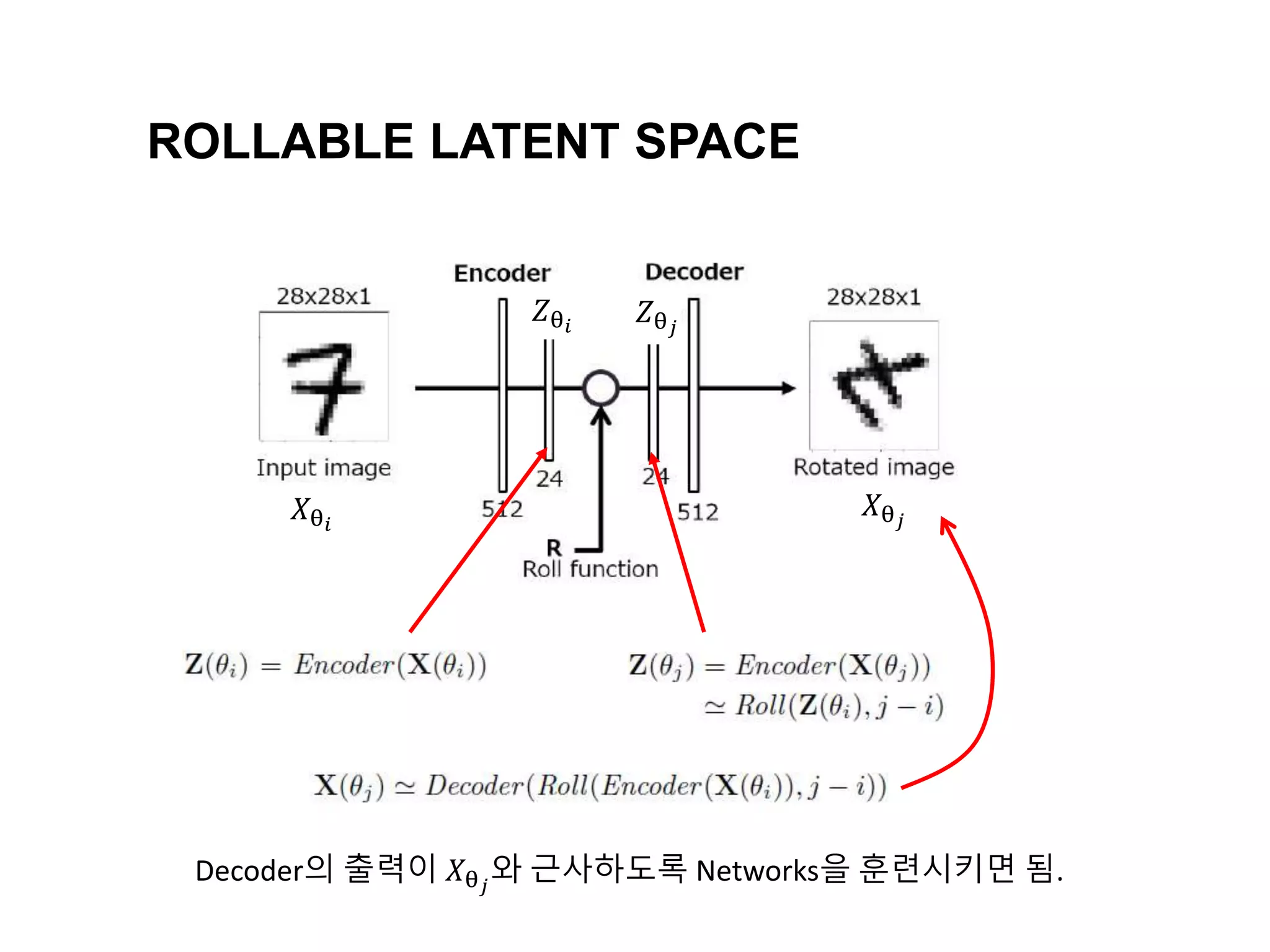
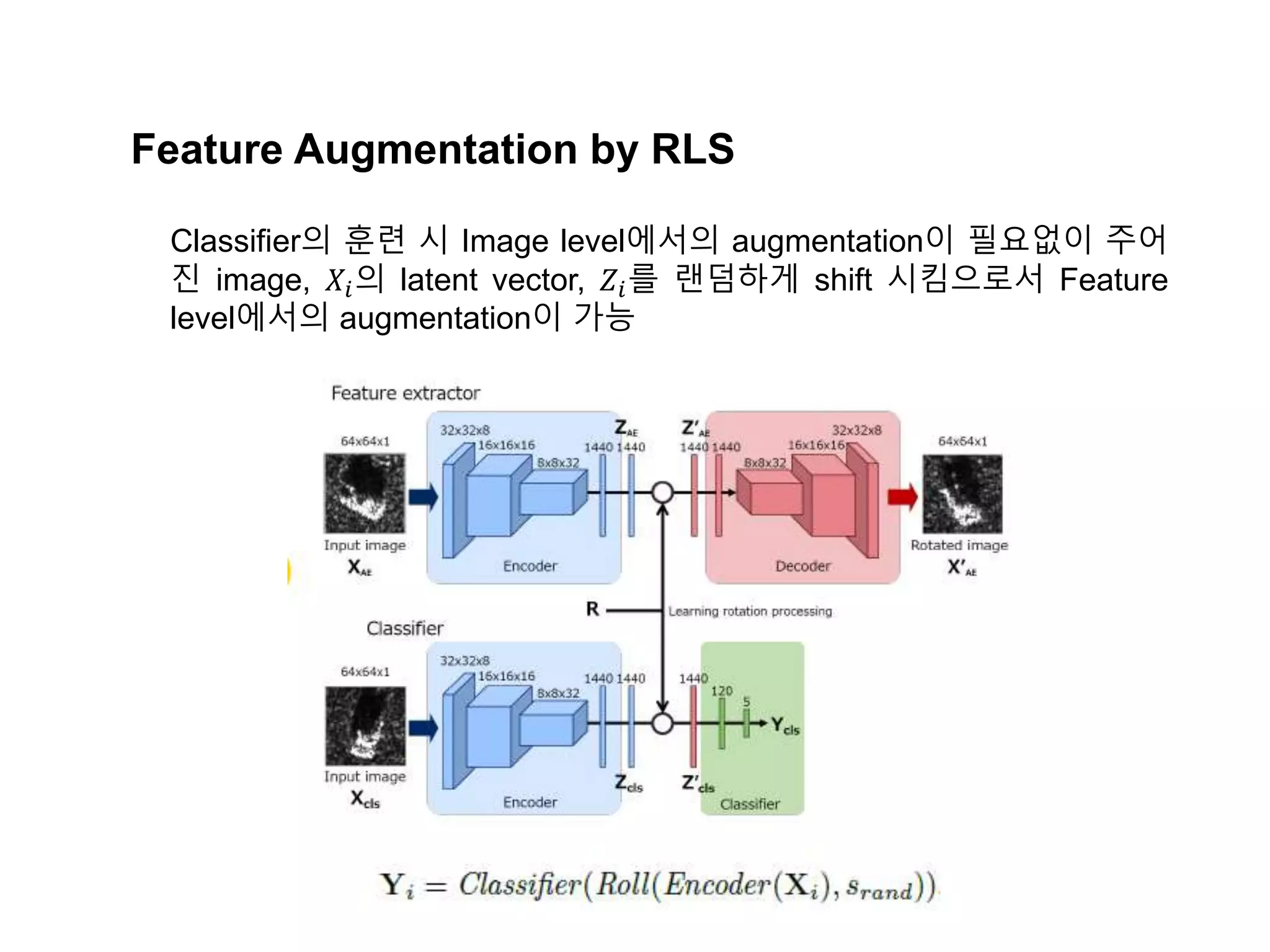
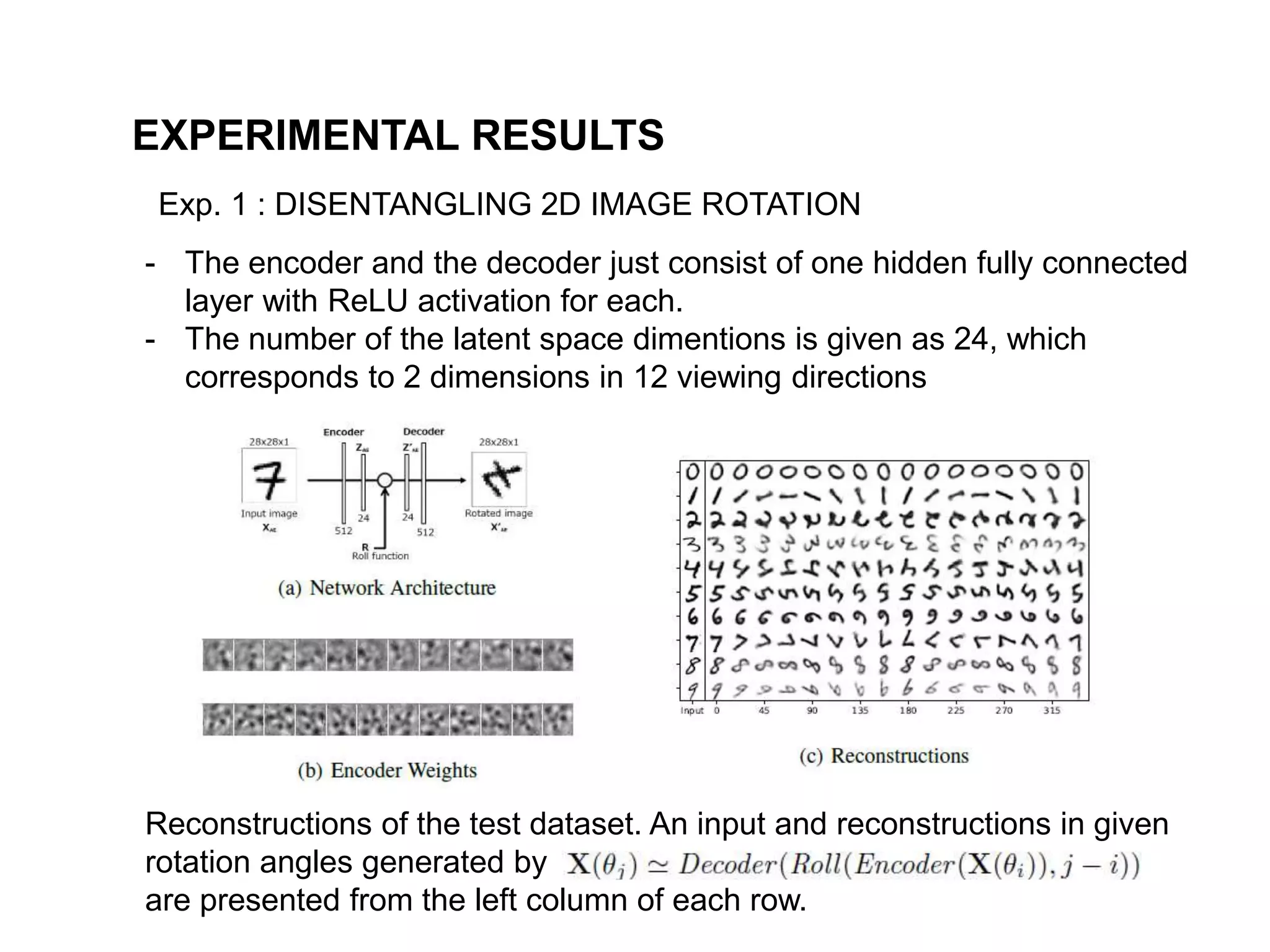
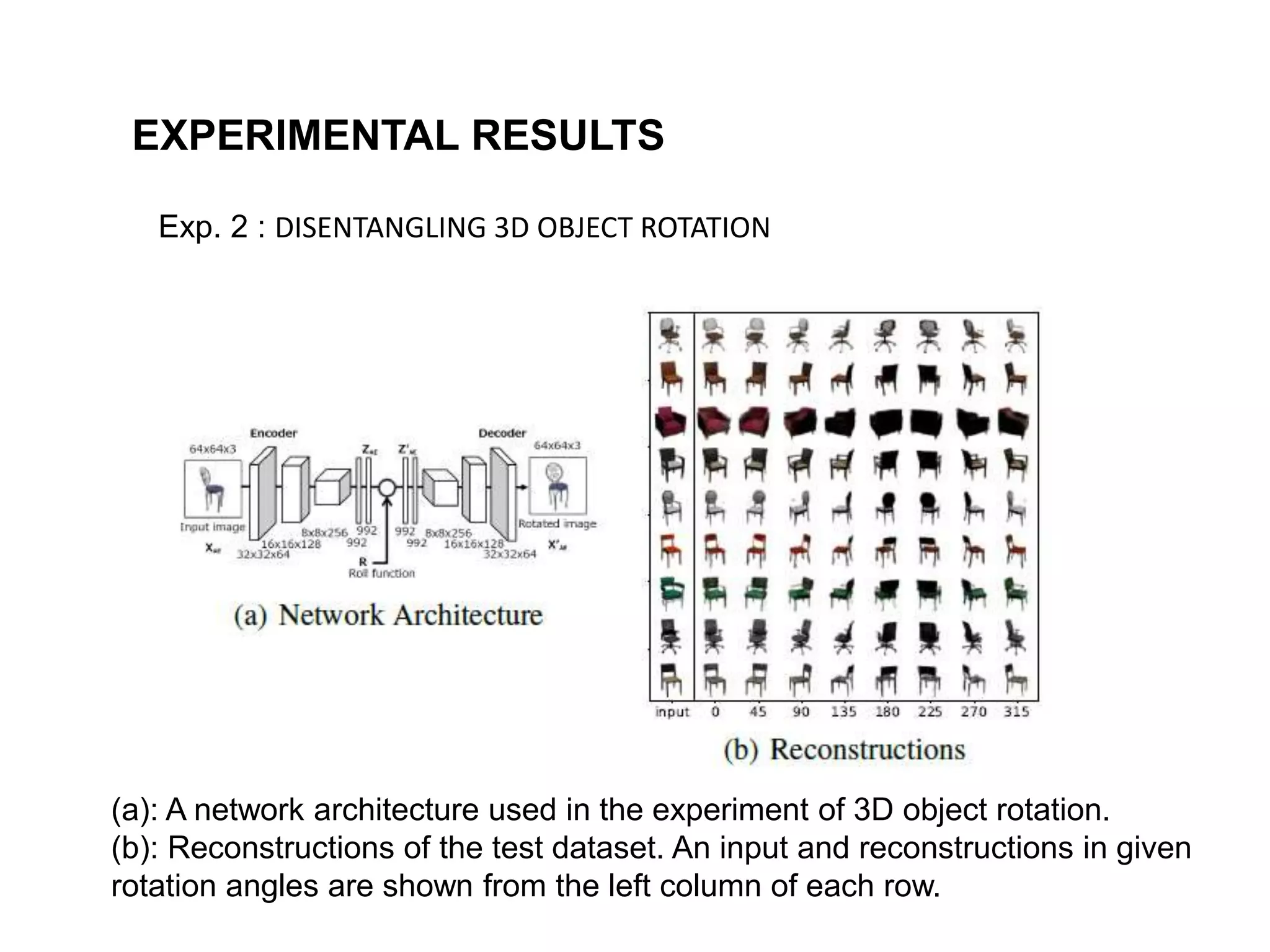
The document discusses a method for disentangling object identity from posture information using a rollable latent space approach, which enables the training of networks without high costs typically associated with acquiring various pose images. It presents a modified auto-encoder that maps angular rotations in the image space to shifts in the latent vector space, allowing for effective feature augmentation and the inference of latent vectors for untrained poses. Experimental results demonstrate the effectiveness of this method through 2D and 3D object rotation reconstructions.

1. ARCHITECTURAL CONDITIONING
FOR DISENTANGLEMENT OF OBJECT
IDENTITY AND POSTURE INFORMATION
저자 : Kazutoshi Sagi, Takahiro Toizumi & Yuzo Senda
Data Science Research Laboratories
NEC Corporation
https://openreview.net/forum?id=HkaYjG6Lf
정리 : 김홍배

2. 일반적으로 다양한 pose에 대한 image를 획득하여 Networks을
Pose에 대하여 Invariance하게 Training  High cost approach
3D Object Identification Problem

3. Equivariance
Φ
Image(X)
Latent(Z) Z1 Z2
𝑇𝑔
2
𝑇𝑔
1
Φ
Transformation
X1 X2
Z2 = 𝑻 𝒈
𝟐
Z1 = 𝑻 𝒈
𝟐
Φ(X1) = Φ(𝑻 𝒈
𝟏
X1 )
: Invariance is special case of equivariance where 𝑇𝑔
2 is the identity.
X2 = 𝑇𝑔
1
X1
Z2 = 𝑇𝑔
2
Z1
: 주어진 Image의 pose변환에 대하여 Latent space상에서
명확한 변환관계를 찾을 수 있다면 ?
Z1 ≠ Z2 but keeps the relationship
Mapping
ft’n(Φ(·))

4. ROLLABLE LATENT SPACE
0
1
2
3
4
5
6
7
8
9
10
11
0 1 2 3 4 5 6 7 8 9 10 11
0
1
2
3
4
5
6
7
8
9
10
11
Image Latent vector
Shift by
circular permutation
Angular
rotation
본 연구에서 제시한 아이디어
3 4 5 6 7 8 9 10 11 0 1 2
𝑋θ 𝑖
𝑋θ 𝑗
𝑍θ 𝑖
𝑍θ 𝑗

5. ROLLABLE LATENT SPACE
Image space에서의 pose 변경(Angular rotation)이 Latent vector의
Circular Permutation에 의한 Shift로 나타낼 수 있다면 ?
 2 space의 Mapping 관계를 명확하게 알 수 있으며
Training하지않은 다른 pose에서의 latent vector를 유추할 수 있다 !
 여기서는 Auto-Encoder를 살짝 바꿔서 강제로 학습을 시킨다

6. ROLLABLE LATENT SPACE
𝑋θ 𝑖
𝑋θ 𝑗
𝑍θ 𝑖
𝑍θ 𝑗
여기서 Roll(Z, s)는 𝑍θ 𝑖
를 shift parameter s(각도 차) 만큼 Cyclic
permutation 시킨 후 Decoder쪽의 입력 latent vector로 준다.
Encoder쪽 입력에 𝑋θ 𝑖
를 Decoder 쪽 출력에는 회전한 𝑋θ 𝑗
를 준다.

7. ROLLABLE LATENT SPACE
𝑋θ 𝑖
𝑋θ 𝑗
𝑍θ 𝑖
𝑍θ 𝑗
Decoder의 출력이 𝑋θ 𝑗
와 근사하도록 Networks을 훈련시키면 됨.

8. Feature Augmentation by RLS
Classifier의 훈련 시 Image level에서의 augmentation이 필요없이 주어
진 image, 𝑋𝑖의 latent vector, 𝑍𝑖를 랜덤하게 shift 시킴으로서 Feature
level에서의 augmentation이 가능

9. EXPERIMENTAL RESULTS
- The encoder and the decoder just consist of one hidden fully connected
layer with ReLU activation for each.
- The number of the latent space dimentions is given as 24, which
corresponds to 2 dimensions in 12 viewing directions
Exp. 1 : DISENTANGLING 2D IMAGE ROTATION
Reconstructions of the test dataset. An input and reconstructions in given
rotation angles generated by
are presented from the left column of each row.

10. EXPERIMENTAL RESULTS
Exp. 2 : DISENTANGLING 3D OBJECT ROTATION
• 809 chair models are selected
• The first 500 models are used as a training set and the remaining 309 models
are used as a test set.
• Each chair model is rendered from 31 azimuth angles and 2 elevation angles
(20 and 30)
• A deep convolutional encoder-decoder architecture are used.
• The number of the latent space dimensions is given as 992, which corresponds
to 32 dimensions in 31 viewing directions.

11. EXPERIMENTAL RESULTS
Exp. 2 : DISENTANGLING 3D OBJECT ROTATION
(a): A network architecture used in the experiment of 3D object rotation.
(b): Reconstructions of the test dataset. An input and reconstructions in given
rotation angles are shown from the left column of each row.