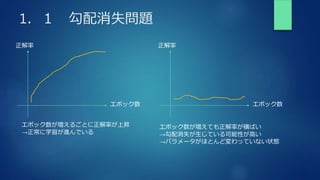
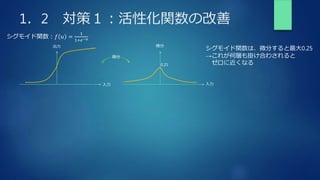
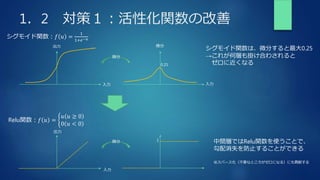
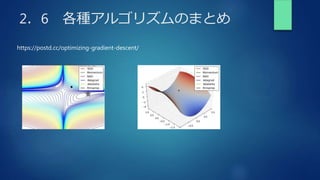
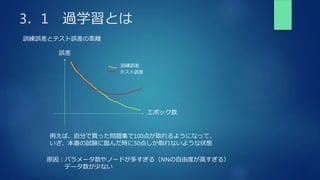
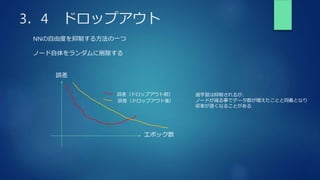
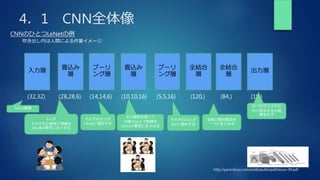
The document summarizes key concepts from a deep learning training, including gradient descent problems and solutions, optimization algorithms like momentum and Adam, overfitting and regularization techniques, and convolutional neural networks (CNNs). Specifically, it discusses gradient vanishing and exploitation issues, activation function and weight initialization improvements, batch normalization, optimization methods, overfitting causes and regularization countermeasures like dropout, and a basic CNN architecture overview including convolution, pooling and fully connected layers.







![2.2 モメンタム
𝑽𝑘 = 𝜇𝑽𝑘−1 − ε𝛻𝐸
前回の𝐰の変化量に𝜇を掛けて加算する。移動平均のような動きをする。
局所解に停滞しにくい
𝒘𝑘+1 = 𝒘𝑘 + 𝑽𝑘
参考
【機械学習】パラメータ更新の最適化#モメンタム
(𝜇を慣性項という)
v[k] = momentum * v[k] - learning_rate * grad[k]
実装例
w[k] += v[k]](https://image.slidesharecdn.com/rabbitchallenge4dnn2-210429131718/85/Rabbit-challenge-3-DNN-Day2-11-320.jpg)
![2.3 AdaGrad
ℎ𝑡 = ℎ𝑡−1+(𝛻𝐸)2
勾配の緩やかな斜面に対して学習が進みやすいが、
大域最適解にたどり着かず、鞍点問題を引き起こしやすい(学習率が徐々に小さくなるため)
𝒘𝑡+1 = 𝒘𝑡 − 𝜀
1
ℎ𝑡
𝛻𝐸
参考
【機械学習】パラメータ更新の最適化#AdaGrad
これまでの重みの更新の記憶
h[k] += grad[k]**2
実装例
w[k] - = (learning_rate * grad[k]) / np.sqrt(h[k] + 1e-7)](https://image.slidesharecdn.com/rabbitchallenge4dnn2-210429131718/85/Rabbit-challenge-3-DNN-Day2-12-320.jpg)
![2.4 RMSProp
ℎ𝑡 = 𝛼ℎ𝑡−1+(1 − 𝛼)(𝛻𝐸)2
AdaGradの鞍点問題に陥りやすいデメリットを改善
AdaGradの場合の初期値をうまく調整する必要があったのに対し、
RMSPropはその調整が簡単になった。
𝒘𝑡+1 = 𝒘𝑡 − 𝜀
1
ℎ𝑡
𝛻𝐸
𝛼ℎ𝑡−1前回の重みの更新の記憶
(1 − 𝛼)(𝛻𝐸)2
今回の重み更新
h[k] *= decay_rate
実装例
w[k] - = (learning_rate * grad[k]) / np.sqrt(h[k] + 1e-7)
こちらはAdaGradと一緒
#𝛼ℎ𝑡−1
h[k] +=(1 - decay_rate)*grad[k]**2 #(1 − 𝛼)(𝛻𝐸)2](https://image.slidesharecdn.com/rabbitchallenge4dnn2-210429131718/85/Rabbit-challenge-3-DNN-Day2-13-320.jpg)
![2.5 Adam
𝑚𝑡 = 𝛽1𝑚𝑡−1+(1 − 𝛽1)𝛻𝐸
モメンタム + RMSPropの良いところ取り
𝒘𝑡+1 = 𝒘𝑡 − 𝜀
1
𝑣𝑡
𝑚𝑡
勾配の1乗の記憶
m[k] += (1-beta1)*(grad[k] - m[k])
実装例
w[k] - = (learning_rate * m[k]) / np.sqrt(v[k] + 1e-7)
こちらはAdaGradやRMSPropと類似
(𝛻𝐸が前回の記憶値𝑚𝑡に代わっている)
𝑣𝑡 = 𝛽2𝑣𝑡−1+(1 − 𝛽2)(𝛻𝐸)2 勾配の2乗の記憶
m[k] = m[k] + (1-beta1)*(grad[k]) - (1-beta1)*m[k]
= beta1*m[k] + (1-beta1)*(grad[k])
v[k] += (1-beta2)*(grad[k]**2 - v[k])](https://image.slidesharecdn.com/rabbitchallenge4dnn2-210429131718/85/Rabbit-challenge-3-DNN-Day2-14-320.jpg)


![3.3 正則化 実装例
s[k] = np.sign(w[k])
L1ノルム(Lasso)実装例
grad[k] += rate * s[k]
1
𝑝
𝜆 𝑤 𝑝 で𝑝 = 1ならば、𝑤は一次のみなので、
勾配すなわち微分を求めると𝜆 × ±1となる。
L2ノルム(Ridge)実装例
1
𝑝
𝜆 𝑤 𝑝 で𝑝 = 2ならば、𝑤は二次のみなので、
勾配すなわち微分を求めると𝜆 × 𝑤となる。
ここで、微分で出てきた係数は𝜆に吸収されると考えて良い
grad[k] += rate * w[k]](https://image.slidesharecdn.com/rabbitchallenge4dnn2-210429131718/85/Rabbit-challenge-3-DNN-Day2-19-320.jpg)

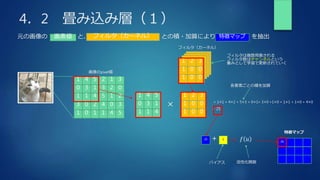


![4.6 実装 畳込み層の高速化施策
1 4 5 2
0 3 1 3
1 1 4 5
3 0 2 4
1 4 5 0 3 1 1 1 4
4 5 2 3 1 3 1 4 5
0 3 1 1 1 4 3 0 2
3 1 3 1 4 5 0 2 4
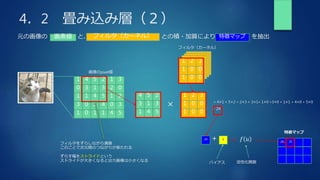
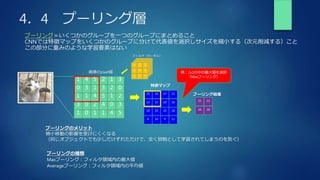
畳み込みされる領域をフィルタのサイズで区切って一列に並べる
これにより、フィルタとの掛け算の和は単純な配列の積と和になる
def im2col(input_data, filter_h, filter_w, stride=1, pad=0):
N, C, H, W = input_data.shape
out_h = ( (H + 2*pad - filter_h) // stride ) + 1
out_w = ( (W + 2*pad - filter_w) // stride ) + 1
img = np.pad( input_data, [(0,0), (0,0), (pad, pad), (pad, pad)], 'constant')
col = np.zeros((N, C, filter_h, filter_w, out_h, out_w))
for y in range(filter_h):
y_max = y + stride * out_h
for x in range(filter_w):
x_max = x + stride * out_w
col[:, :, y, x, :, :] = img[:, :, y:y_max:stride, x:x_max:stride]
# (N, C, filter_h, filter_w, out_h, out_w) - > (N, filter_w, out_h, out_w, C, filter_h)
col = col.transpose(0, 4, 5, 1, 2, 3)
col = col.reshape(N * out_h * out_w, -1)
return col
畳み込みの出力データサイズを計算(上の例だと2×2)
元データにパディングを追加
この関数の出力配列(畳み込み領域を一列に並べた配列)
フィルタ幅高さ分だけ一つずつずらすため、
一回の取り出しサイズの上限を計算
(上の例だと、y_max,x_maxとも2,3,4)
元の画像を(x:x_max)×(y:y_max)で取り出す(stride分飛ばしながら)
フィルタサイズの幅高さに並べ替え、一列にreshape](https://image.slidesharecdn.com/rabbitchallenge4dnn2-210429131718/85/Rabbit-challenge-3-DNN-Day2-28-320.jpg)
![4.7 実装 プーリング層の逆伝播
Poolingクラス
def forward(self, x):
N, C, H, W = x.shape
out_h = int(1 + (H - self.pool_h) / self.stride)
out_w = int(1 + (W - self.pool_w) / self.stride)
# xを行列に変換
col = im2col(x, self.pool_h, self.pool_w, self.stride, self.pad)
# プーリングのサイズに合わせてリサイズ
col = col.reshape(-1, self.pool_h*self.pool_w)
# 行ごとに最大値を求める
arg_max = np.argmax(col, axis=1)
out = np.max(col, axis=1)
# 整形
out = out.reshape(N, out_h, out_w, C).transpose(0, 3, 1, 2)
self.x = x
self.arg_max = arg_max
return out
def backward(self, dout):
dout = dout.transpose(0, 2, 3, 1)
pool_size = self.pool_h * self.pool_w
dmax = np.zeros((dout.size, pool_size))
dmax[np.arange(self.arg_max.size), self.arg_max.flatten()] = dout.flatten()
dmax = dmax.reshape(dout.shape + (pool_size,))
dcol = dmax.reshape(dmax.shape[0] * dmax.shape[1] * dmax.shape[2], -1)
dx = col2im(dcol, self.x.shape, self.pool_h, self.pool_w, self.stride, self.pad)
return dx
プーリングの出力データサイズを計算
高速化のために一行にする
Maxプーリング処理
(argmaxは一行の中の最大値のindexが入る。)
arg_max(index)の部分にdoutが入る
(Reluの微分のような感じ)](https://image.slidesharecdn.com/rabbitchallenge4dnn2-210429131718/85/Rabbit-challenge-3-DNN-Day2-29-320.jpg)


