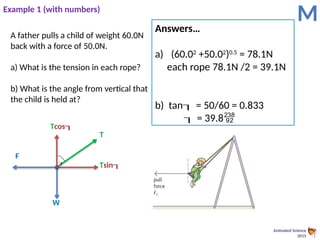
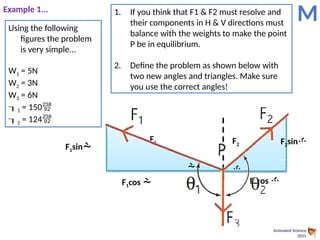
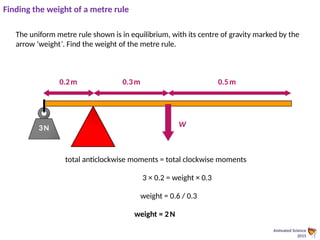
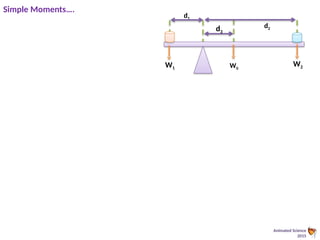
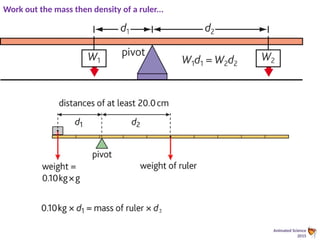
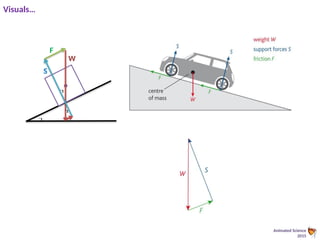
This document provides an overview of the principles of static equilibrium, focusing on vector and scalar quantities, the principles of moments, and the conditions required for a body to be in equilibrium. It includes learning objectives, mathematical techniques, and practical applications involving forces in different contexts, along with numerous example problems. The content is structured to guide students in understanding and applying these concepts in physics.