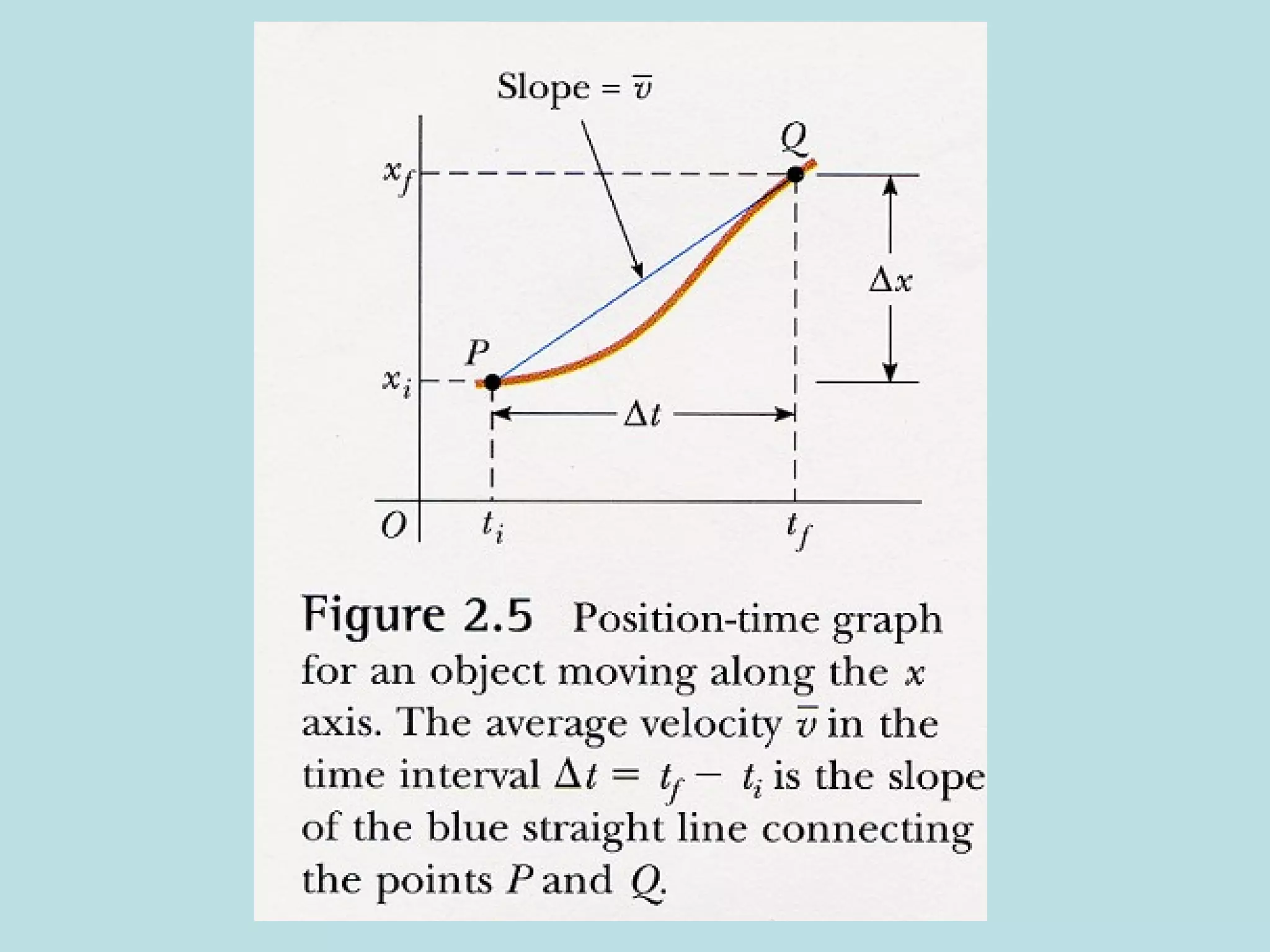
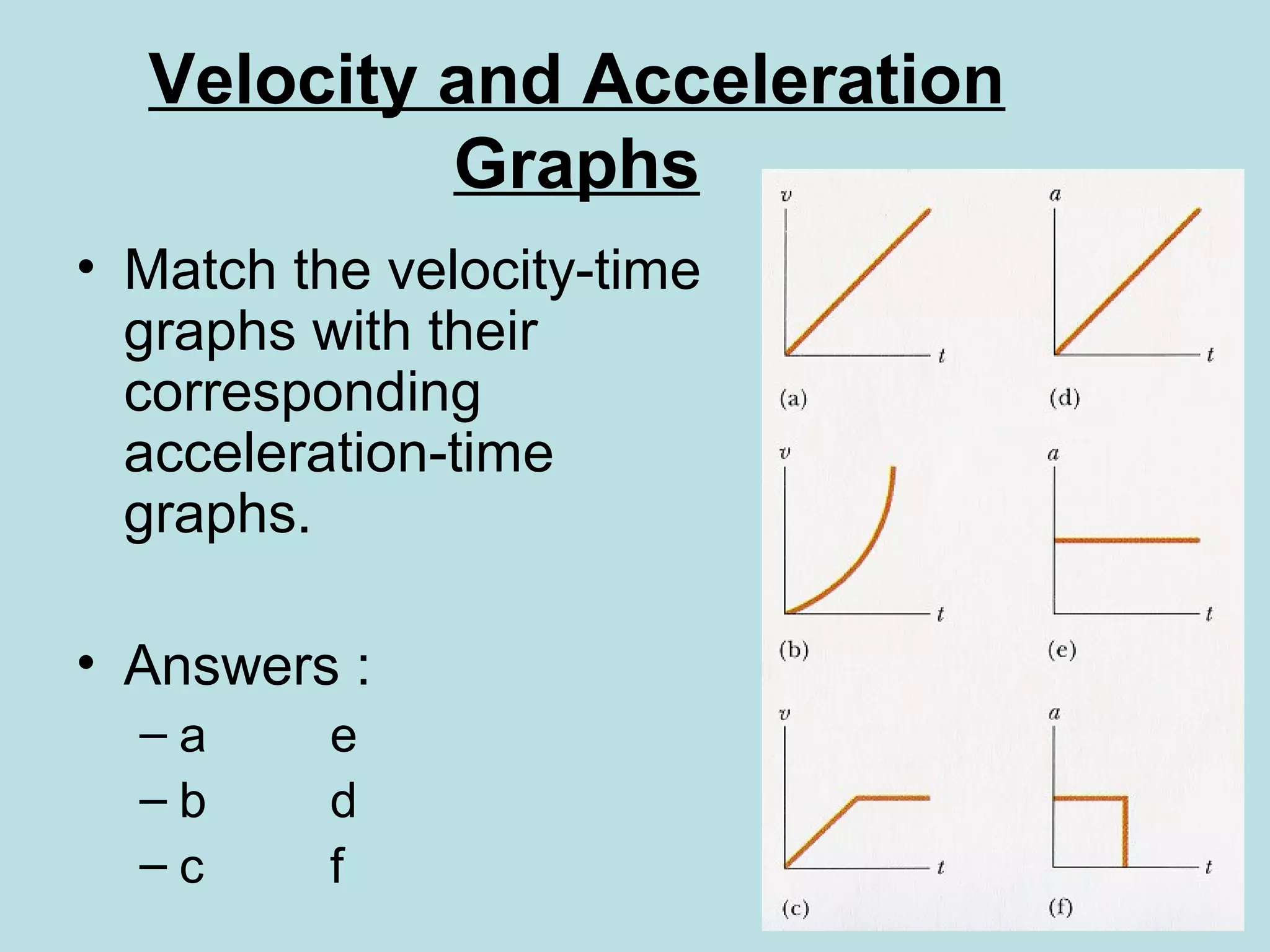
This document defines key concepts related to motion in one dimension, including scalar and vector quantities, displacement, distance, velocity, acceleration, and free fall. Displacement is a vector quantity that describes the change in an object's position, while distance is a scalar quantity referring to how far an object moves. Velocity and acceleration can be average or instantaneous, and their relationships as well as graphical representations are explained. Free fall describes the motion of objects under the influence of gravity alone. Practice problems apply these concepts to real-world scenarios.

1. Motion in One Dimension

2. Scalar and Vector Quatities
• Vector- a physical quantity that requires
the specification of both magnitude and
direction.
• Scalar- a physical quantity that requires
only magnitude.

3. Displacement
• Is the change in position of an object.
• Is given by the difference between an
objects final and initial coordinates.
• Symbol – Δx
– Where Δ is the symbol for “the change in”
• Δx = xFinal- xinitial
• Units – meter (m)
• Vector quantity

4. Distance
• Is how far an object moves.
• The path that the object travels matters.
• Units – meter (m)
• Symbol – d
• Scalar quantity

5. Sign Convention
• When dealing with motion in one
dimension, the object only has two
direction to travel. These two directions
are specified by using + and – signs.
• If the sign of the motion is + the object is
moving in the +x direction. Likewise, if the
sign of the motion is - the object is moving
in the -x direction.

6. Average Velocity
• Is the displacement, Δx, divided by the
time interval during which the
displacement occurred.
• Equation:
• Units m/s

7. Instantaneous Velocity
• The limit of the average velocity as the
time interval Δt becomes infinitesimally
short.
• Equation:
• Units m/s

8. Graphical Representation of
Average Velocity
• The slope of a position vs. time graph
gives the average velocity of an object.
• For any object, the average velocity during
the time interval ti to tf is equal to the slope
of the straight line joining the initial and
final points on a graph of the position of
the object plotted vs. time.

10. Graphical Representation of
Instantaneous Velocity
• The instantaneous
velocity is defined as
the slope of the line
tangent to the position-
time curve at P.

11. A toy train moves slowly
along a straight
portion of track
according to the graph
of position vs. time to
the right.
Find
• the average velocity for the total trip.
• the average velocity for 0.0 s- 4.0 s.
• the average velocity for 4.0 s- 8.0 s.
• the average velocity for 8.0 s- 12.0 s.
• the instantaneous velocity at t = 2.0 s.
• the instantaneous velocity at t = 5.0 s.

12. Average Acceleration
• The change in velocity during the time
interval during which the change occurs.
• Equation:
• Units: m/s2

13. Instantaneous Acceleration
• The limit of the average acceleration as
the time interval Δt becomes infinitesimally
short.
• Equation:
• Units m/s2

14. Acceleration and Velocity
• When the object’s velocity and
acceleration are in the same direction, the
speed of the object will increase with time.
• When the object’s velocity and
acceleration are in opposite directions, the
speed of the object will decrease with
time.

15. Motion Maps
One way to describe motion is through a
diagram called a motion map. Many
different types of motion maps exist, we
will start with a simple one.

17. Graphical Representation of
Average Acceleration
• The slope of a velocity vs. time
graph gives the average
acceleration of an object.
• For any object, the average
acceleration during the time
interval ti to tf is equal to the slope
of the straight line joining the initial
and final points on a graph of the
velocity of the object plotted vs.
time.

18. Graphical Representation of
Instantaneous Acceleration
• The instantaneous acceleration of an
object is equal to the slope of the velocity-
time graph at that instant in time.
• From now on we will use “acceleration” to
mean “average acceleration” .

19. A baseball player moves
in a straight line path in
order to catch a fly ball
hit into the outfield. His
velocity as a function of
time is shown in the
graph.
A) Find his instantaneous acceleration at points
A,B,C on the curve.
B) Describe in everyday language how the outfielder
is moving.

20. Velocity and Acceleration
Graphs
• Match the velocity-time
graphs with their
corresponding
acceleration-time
graphs.
• Answers :
– a e
– b d
– c f

21. Freefall
•Is when an object is moving under the
influence of gravity alone. The source of
the initial motion is not important.
•Objects that are thrown upward,
downward or released from rest are all in
freefall once released.

22. • Once objects are in freefall they have a
constant acceleration downward, which is
the acceleration due to gravity, g.
• g=9.8m/s2
• g is + or – depending on the definition of
the + direction

23. Freefall Practice Problems
1. A ball is thrown downward from the top of
a cliff with an initial speed of 10.0 m/s.
Determine the velocity and speed of the
ball ay t=2.00s.

24. Freefall Practice Problems
2. A stone is thrown from the top of a building
with an initial velocity of 20.0 m/s upward. The
building is 50.0m high, and the stone just
misses the edge of the roof on the way down.
Determine
• the time to reach the maximum height.
• the maximum height.
• the time needed to return to the throwers
height.
• the velocity of the stone at this height.
• the velocity and position of the stone at t =
5.00s.

25. Freefall
•Is when an object is moving under the
influence of gravity alone. The source of
the initial motion is not important.
•Objects that are thrown upward,
downward or released from rest are all in
freefall once released.

26. • Once objects are in freefall they have a
constant acceleration downward, which is
the acceleration due to gravity, g.
• g=9.8m/s2
• g is + or – depending on the definition of
the + direction

27. Freefall Practice Problems
1. A ball is thrown downward from the top of
a cliff with an initial speed of 10.0 m/s.
Determine the velocity and speed of the
ball ay t=2.00s.

28. Freefall Practice Problems
2. A stone is thrown from the top of a building
with an initial velocity of 20.0 m/s upward. The
building is 50.0m high, and the stone just
misses the edge of the roof on the way down.
Determine
• the time to reach the maximum height.
• the maximum height.
• the time needed to return to the throwers
height.
• the velocity of the stone at this height.
• the velocity and position of the stone at t =
5.00s.