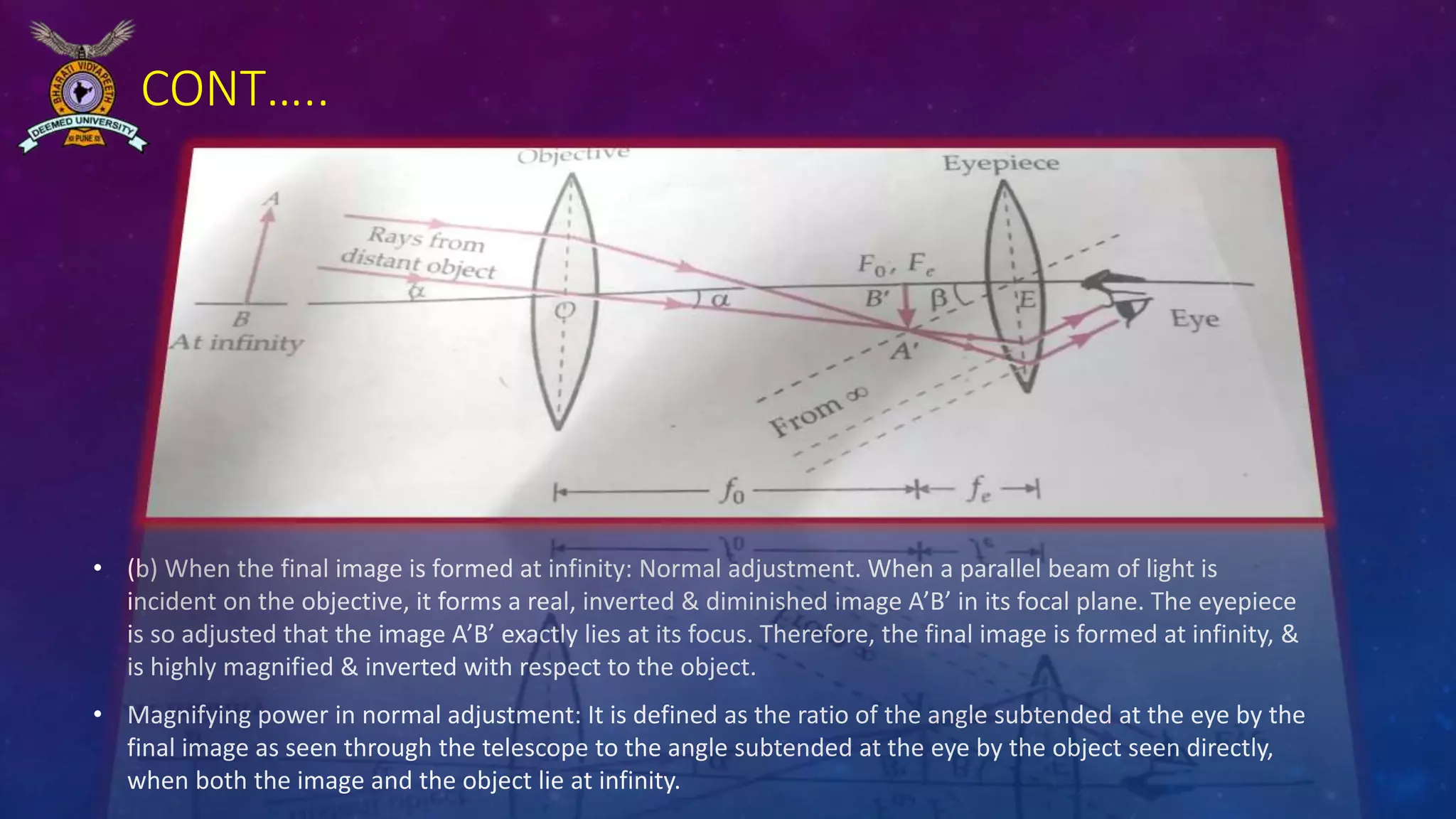
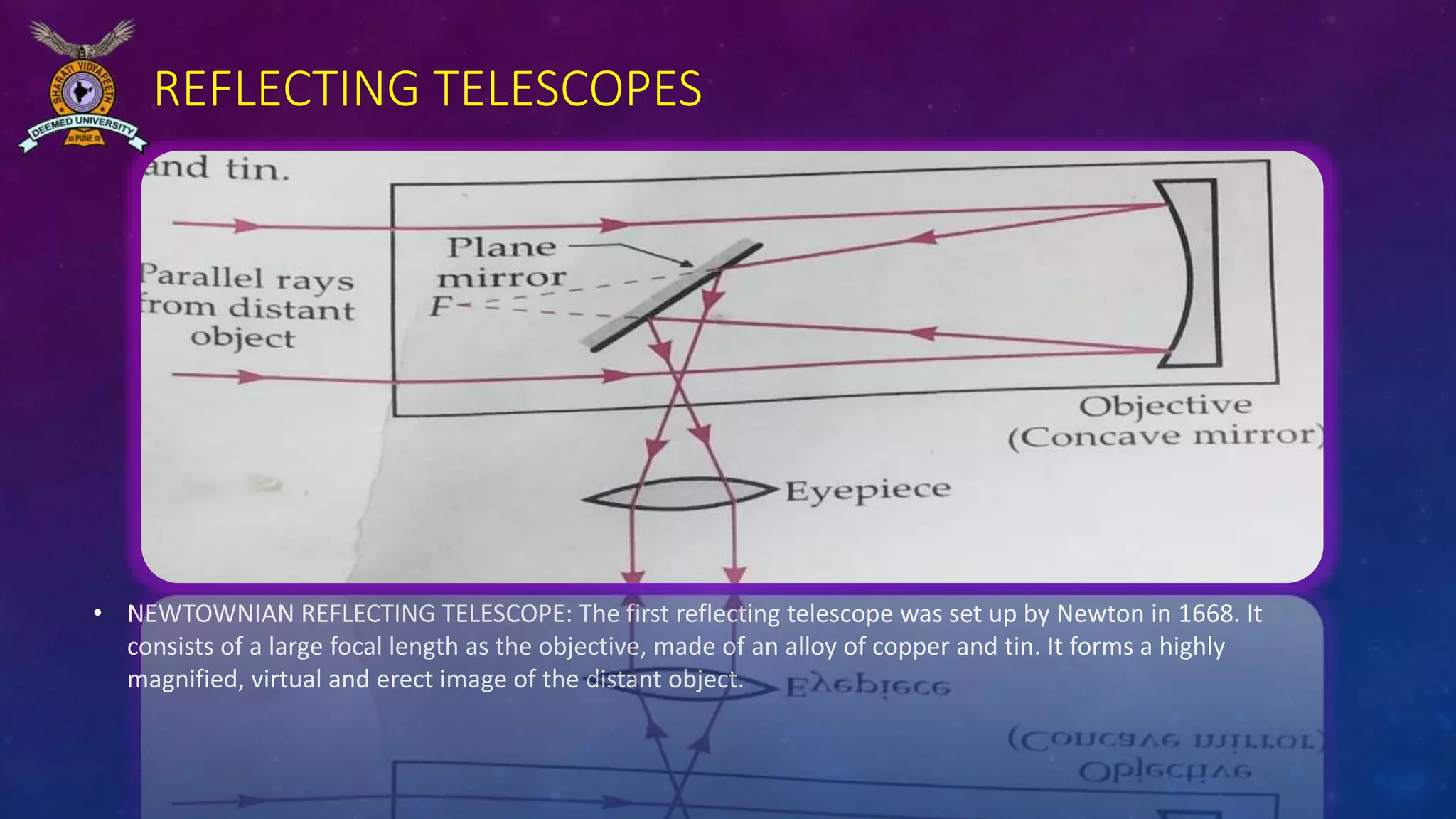
The document discusses angular magnification in microscopes and telescopes, explaining how simple magnifiers and compound microscopes achieve magnification through lens placement and focal length adjustments. It outlines the working principles of refracting and reflecting telescopes, including astronomical and terrestrial types, detailing how they create clear images of distant objects. Key formulas for calculating magnifying power and the construction of these optical devices are also provided.

1. ANGULAR
MAGNIFICATION OF
MICROSCOPE AND
TELESCOPE
BY ANJALI NAIR & TANISHKA PRASAD
( B.OPTOM 1ST YEAR)

2. ANGULAR MAGNIFICATION
• the ratio of the angle subtended at the eye by the image formed by an optical instrument to that
subtended at the eye by the object when not viewed through the instrument.
• A plus lens is used as a simple magnifier.
• The simple magnifier achieves angular magnification by permitting the placement of the object closer
to the eye than the eye could normally focus. The standard close focus distance is taken as 25 cm.

3. SIMPLE MICROSCOPE
• Microscope is an optical instrument which forms large image close and minute objects.
• A simple microscope or a magnifying glass is just a convex lens of short focal length, held close to the
eye.
• When an object is at a distance equal to the focal length of the lens, the image is formed at infinity.
• When an object is at a distance less than the focal length of the lens, the image obtained is virtual, erect
and magnified.

4. ANGULAR MAGNIFICATION OF SIMPLE MICROSCOPE
1. When the final image is formed at the least distance of distinct vision:
• When an object “AB” is placed between the focus ‘F’ & optical centre ‘O’ of a convex lens; a virtual, erect &
magnified image A’B’ is formed on the same side of the lens as the object. Since a normal eye can see an
object clearly at the least distance of distinct vision D {=25CM} , the position of the lens is so adjusted that
the final image is formed at the distance ‘D’ from the lens.

5. CONT…..
• Magnifying power: the magnifying power of a simple microscope is defined as the ratio of the angles subtended by the
image and the object at the eye, when both are at the least distance of distinct vision from the eye.
• As the eye is held close to the lens, the angles subtended at the lens may be taken to be the angles subtended at the
eye. The image A’B’ is formed at the least distance of distinct vision ‘D’. Let ∠A’OB’ = β. Imagine the object AB to be
displaced to position ∠A’’OB’ = α. Then magnifying power,
m=β/α = tanβ/tanα = AB/OB÷A’’B’/OB’ = AB/OB÷AB/OB’ = OB’/OB = -D/-x = D/x
Let ‘f’ be the focal length of the lens. As the image is formed at the least distance of distinct vision from the lens, so
v= -D
Using thin lens formula,
1/v-1/u=1/f
We get, 1/-D – 1/-x= 1/f
or, 1/x= 1/D+1/f
or, D/x= 1+D/f
Therefore, m= 1+D/f
Thus shorter the focal length of the convex lens, the greater is its magnifying power.

6. CONT….
1. When the final image is formed at infinity:
When we see an image at the near point, it causes some strain in the eye. Often the object is placed at the
focus at the convex lens, so that parallel rays enter the eye. The image is formed at infinity, which is more
suitable & comfortable for viewing by the relaxed eye.

7. CONT…..
• Magnifying power: It is defined as the ratio of the angle formed by the image (when situated at infinity) at
the eye to the angle formed by the object at the eye, when situated at the least distance of distinct vision.
m= β/α = tanβ/tanα
tanβ = h/f
tanα = h/D
m= h/f ÷ h/D
m= D/f
Thus magnification is one less than the magnifying when the image is formed at the near point. But viewing
is more comfortable when the eye is focussed at infinity.

8. COMPOUND MICROSCOPE
• A compound microscope is an optical device used to see magnified images of tiny objects. A good quality
compound microscope can produce magnification of the order of 1000.
• It consists of two convex lenses of short focal length, arranged co-axially at the ends of two sliding metal
tubes.
1. Objective: It is a convex lens of very short focal length f0 & small aperture. It is positioned near the object
to be magnified.
2. Eyepiece or ocular: It is a convex lens of comparatively larger focal length fe & larger aperture than the
objective (fe > f0). It is positioned near the eye for viewing the final image.

9. ANGULAR MAGNIFICATION OF COMPOUND MICROSCOPE
1. When the final image is formed at the least distance of distinct vision:
The object AB to be viewed is placed at distance u0 , slightly larger than the focal length f0 of the objective O. the
objective forms a real, inverted & magnified image A’B’, of the object AB on the other side of the lens O. The
separation between the objective O & the eyepiece E, is so adjusted that the image A’B’ lies within the focal length
fe of the eyepiece. The image A’B’ acts as an object for the eyepiece which essentially acts like a simple microscope.
The eyepiece E forms a virtual and magnified final image A’’B’’ of the object AB. Clearly, the final image A’’B” is
inverted with respect to the object AB.

10. CONT….
Magnifying power: The magnifying power of a compound microscope is defined as the ratio of the angle
subtended at the eye by the final virtual image to the angle subtended at the eye by the object, when both
are at the least distance of distinct vision from the eye.
• m= β/α= tanβ/tanα= h’/ue ÷ h/D = h’/h*D/ue = m0me
here, m0= h’/h= v0/u0
As the eyepiece acts as a simple microscope, so
me = D/ue = 1+D/fe
Therefore, m= v0/u0(1+D/fe)
As the object AB is placed close to the focus F0 of the objective, therefore, u0 ͌ -f0
Also the image A’B’ is formed close to the eyelens whose focal length is short, therefore v0 ͌L= the length of
the microscope tube or the distance between the two lenses
Therefore m0 = v0/u0 = L/-f0
Therefore –L/f0(1+D/fe) (for final image at D)

11. CONT….
• When the final image is formed at infinity.
When the image A’B’ lies at the focus Fe‘ of the eyepiece i.e., ue = fe , the image A’’B’’ is formed at infinity.
Magnification due to objective, m0= h’/h = L/-f0
Angular magnification due to eyepiece, me = D/fe
Total magnification when the final image is formed at infinity,
m= m0*me = -L/f0*D/fe
Obviously, magnifying power of the compound microscope is large when both f & f are small.

12. TELESCOPE
• A telescope is an optical device which enables
us to see distant objects clearly.
• It provides an angular magnification of the distant
objects.
• Different types of telescope:
Broadly, the telescope can be divided into two categories:
1. Refracting Telescopes: They make use of lenses to view distant objects.
These are of two types:
(a) Astronomical Telescope
(b) Terrestrial Telescope
2. Reflecting Telescope: These make use of converging mirrors to view the distant objects. For Example,
Newtonian & Cassegrain telescope.

13. ASTRONOMICAL TELESCOPE
• It is a refracting type telescope use to see heavenly bodies like stars, planets, satellites, etc.
• It consists of two converging lenses mounted co-axially at the outer ends of the two sliding tubes.
1. OBJECTIVE
2. EYEPIECE
(a) When the final image is formed at the least distance of distinct vision: The parallel beam of light coming
from the distant object falls on the objective at some angle α. The objective focusses the beam in its focal
plane and forms a real, inverted & diminished image A’B’. The image A’B’ acts as an object for the eyepiece.
The distance of the eyepiece is so adjusted that the image A’B’ lies within its focal length. The eyepiece
magnifies this image so that final image A’’B’’ is magnified & inverted with respect to the object. The final
image is seen distinctly by the eye at the least distance of distinct vision.

14. ANGULAR MAGNIFICATION OF ASTRONOMICAL TELESCOPE
• Magnifying power: The magnifying power of a telescope is defined as the ratio of the angle
subtended at the eye by the final image formed at the least distance of distinct vision to the
angle subtended at the eye by the object at infinity, when seen directly.
• ∠A’OB’= α . Also, Let ∠A’’EB’’= β
Therefore, Magnifying power, m= β/α ͌ tanβ / tanα = A’B’/B’E ÷ A’B’/OB’ = OB’/B’E.
According to the new Cartesian sign convention,
OB’= +f0 = focal length of the objective
B’E= -ue = distance of A’B’ from the eyepiece, acting as an object for it.
Therefore, m= -f0/ue . Again, for the eyepiece: u= -ue & v= -D. As, 1/v-1/u= 1/f.
Therefore, 1/-D-1/-ue = 1/fe . Or, 1/ue = 1/fe+1/D = 1/fe(1+fe/D)
Hence, m= -f /f (1+f /D)

15. CONT…..
• (b) When the final image is formed at infinity: Normal adjustment. When a parallel beam of light is
incident on the objective, it forms a real, inverted & diminished image A’B’ in its focal plane. The eyepiece
is so adjusted that the image A’B’ exactly lies at its focus. Therefore, the final image is formed at infinity, &
is highly magnified & inverted with respect to the object.
• Magnifying power in normal adjustment: It is defined as the ratio of the angle subtended at the eye by the
final image as seen through the telescope to the angle subtended at the eye by the object seen directly,
when both the image and the object lie at infinity.

16. CONT…..
• ∠A’OB’= α , ∠A’EB’= β
• Therefore, Magnifying power, m= β/α = tanβ / tanα = A’B’/B’E ÷ A’B’/OB’= OB’/B’E
Applying new Cartesian sign convention, OB’= +f0 = Distance of A’B’ from the objective along the
incident light
B’E = -fe = Distance of A’B’ from the eyepiece against the incident light.
Therefore, m= -f0/fe

17. TERRESTRIAL TELESCOPE
• It is a refracting type telescope used to see erect images of distant earthly objects. It uses an
additional convex lens between objective & eyepiece for obtaining an erect image.
• When the image is formed at infinity,
m= f0/fe ,
When the image is formed at the least distance of distinct vision,
m= f0/fe(1+fe/D)

18. REFLECTING TELESCOPES
• NEWTOWNIAN REFLECTING TELESCOPE: The first reflecting telescope was set up by Newton in 1668. It
consists of a large focal length as the objective, made of an alloy of copper and tin. It forms a highly
magnified, virtual and erect image of the distant object.

19. CONT.....
• Cassegrain Reflecting Telescope: It consists of a large concave paraboloidal (primary) mirror having a hole
at its center. The eyepiece is placed on the axis of the telescope near the hole of the primary mirror.
• Let f0 be the focal length of the objective & fe that of the eyepiece
• For the final (1+fimage formed at the least distance of distinct vision,
m= f0 /fe (1+fe /D)
When the image formed at infinity:
m= f0 /fe = R/2 ÷ fe