There are four types of conic sections: 1. Ellipses have an equation of the form (x^2/a^2) + (y^2/b^2) = 1. The values of a and b determine the shape and size. 2. Hyperbolas have a similar equation to ellipses but with a minus sign instead of plus, resulting in two branches that extend to infinity. 3. Circles have the equation (x-a)^2 + (y-b)^2 = r^2, where (a,b) are the coordinates of the center and r is the radius. 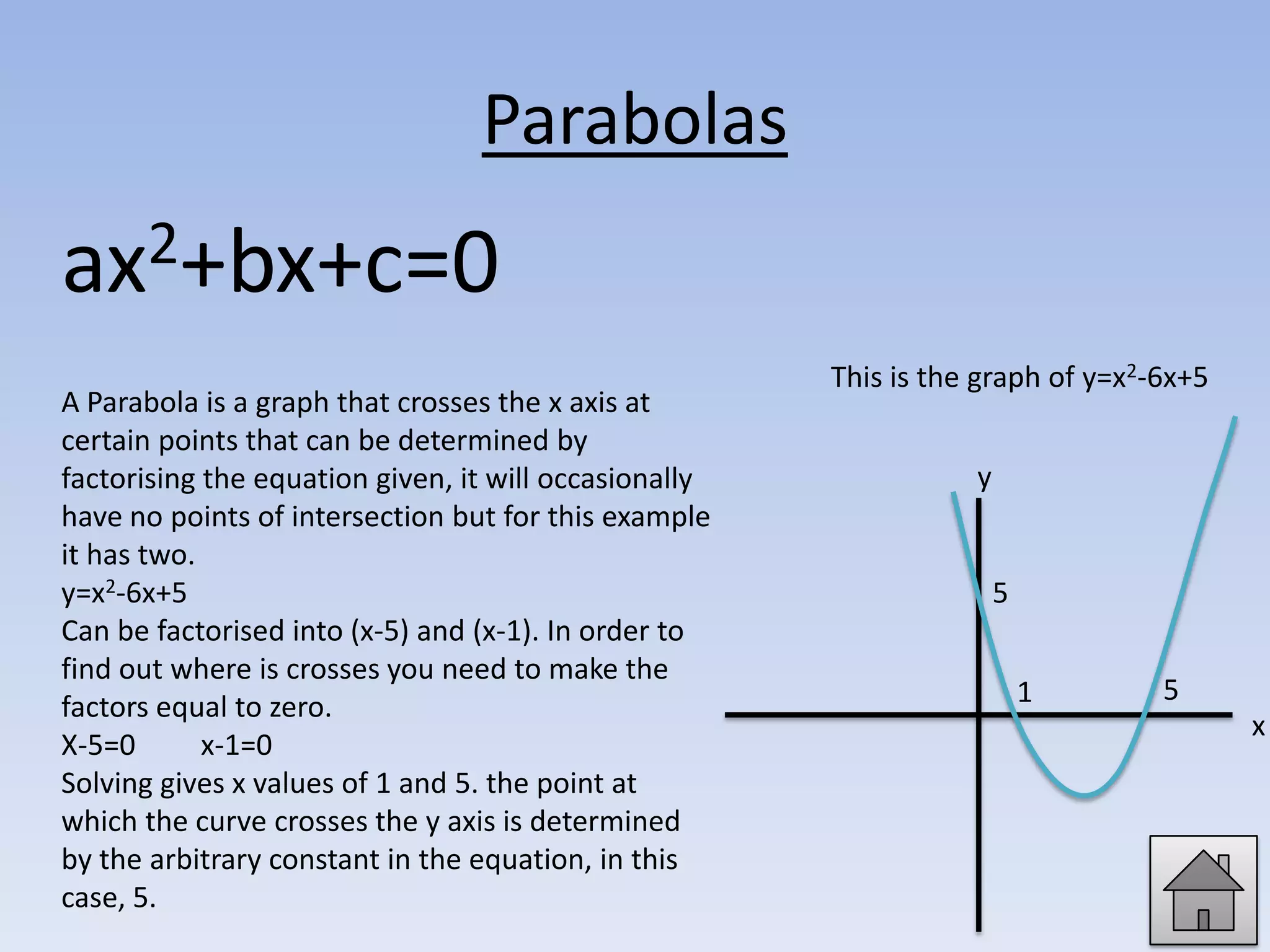4. Parabolas have the general form ax

1. Conics
What are they? What do they look like? What are their equations?
The Word Conic Comes from the shape of a cone and the four examples of “conic
sections” come from taking certain slices out of the 3D cone and observing them
from a 2D perspective. This lets us see certain shapes that we can map onto a graph
with x and y axis that we can translate and reflect.
There are four conic Sections that can be taken from a cone and they are:
Ellipses Hyperbolae Circles Parabolas
By Anderson McCammont 12JA

2. Ellipses
An Ellipse is a shape that is similar to the appearance of an oval. It has the equation of:
x 2 y 2
a2 b2
y
In this example to the right hand side, we can see
that there are two values on the graph. The value of
a is 2 and the value of b is 1. We know this because
as it is “x squared over a squared”, a is paired with x 1
and so the value that lies on the ellipse and on the x
axis is the value of a. The value of b is 1 because, 2
exactly the same as the reason previously stated, x
the value that lies on the ellipse and y axis is the
value of b.

3. Hyperbolae
A Hyperbola has a similar equation to that of an ellipse the only difference being that the
sign is a minus instead of an add. This effects the
Conic so that it looks like the image shown below.
The value of a that is used in the
y hyperbolic equation is where the
hyperbola itself crosses the x axis. This
is a and –a. Using the equations of
y=b/a x and y=-b/a x, you can sub in the
equations of the lines of the asymptotes
and then find b from that which finally
lets you write the hyperbola in the form
x of an equation seen below.
x 2 y 2
a 2 b 2

4. Circles
(x-a)2+(y-b)2=r2
Circles are very different to the other conics as their equation involves radii.
In the case of the other conics, the values of a and b were determined by
The location of the points of intersection, this time the value of a and b are given by
Finding out the centre of the circle in the form (x,y). The x value in this co-ordinate is now
The value of a and the y value is the value of b. R on the other hand is as stated earlier the
value of the radius, squared. Ill give an example:
The centre of a circle is:
(3,4) with radius 5, write this in the form of the equation of a circle.
Using the equation setup and the information given, we can rewrite the data as:
(x-3) 2 + (y-4) 2 =52
This finally becomes: (x-3) 2 + (y-4) 2 =25

5. Parabolas
ax 2+bx+c=0
This is the graph of y=x2-6x+5
A Parabola is a graph that crosses the x axis at
certain points that can be determined by
factorising the equation given, it will occasionally y
have no points of intersection but for this example
it has two.
y=x2-6x+5 5
Can be factorised into (x-5) and (x-1). In order to
find out where is crosses you need to make the
1 5
factors equal to zero.
x
X-5=0 x-1=0
Solving gives x values of 1 and 5. the point at
which the curve crosses the y axis is determined
by the arbitrary constant in the equation, in this
case, 5.