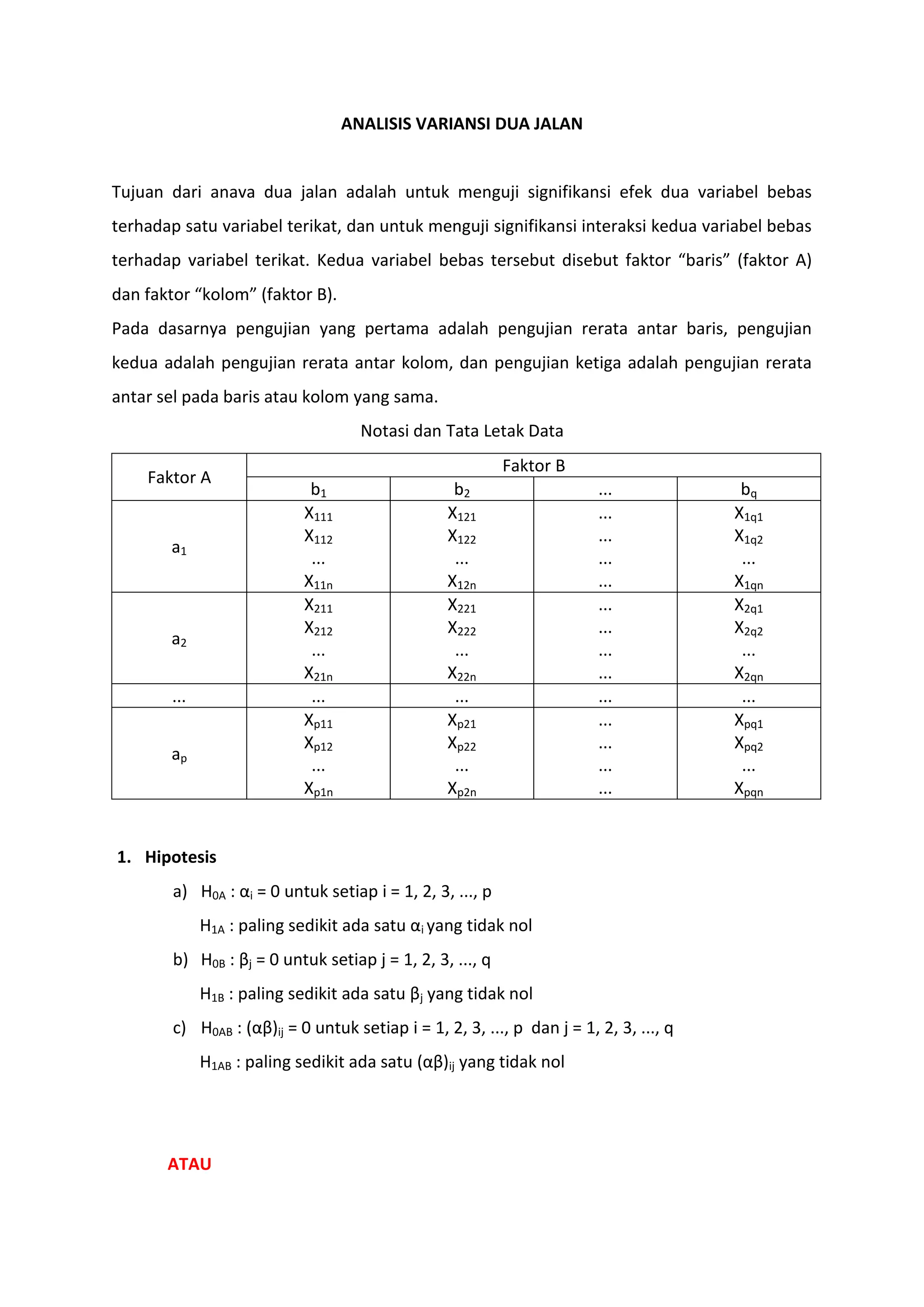
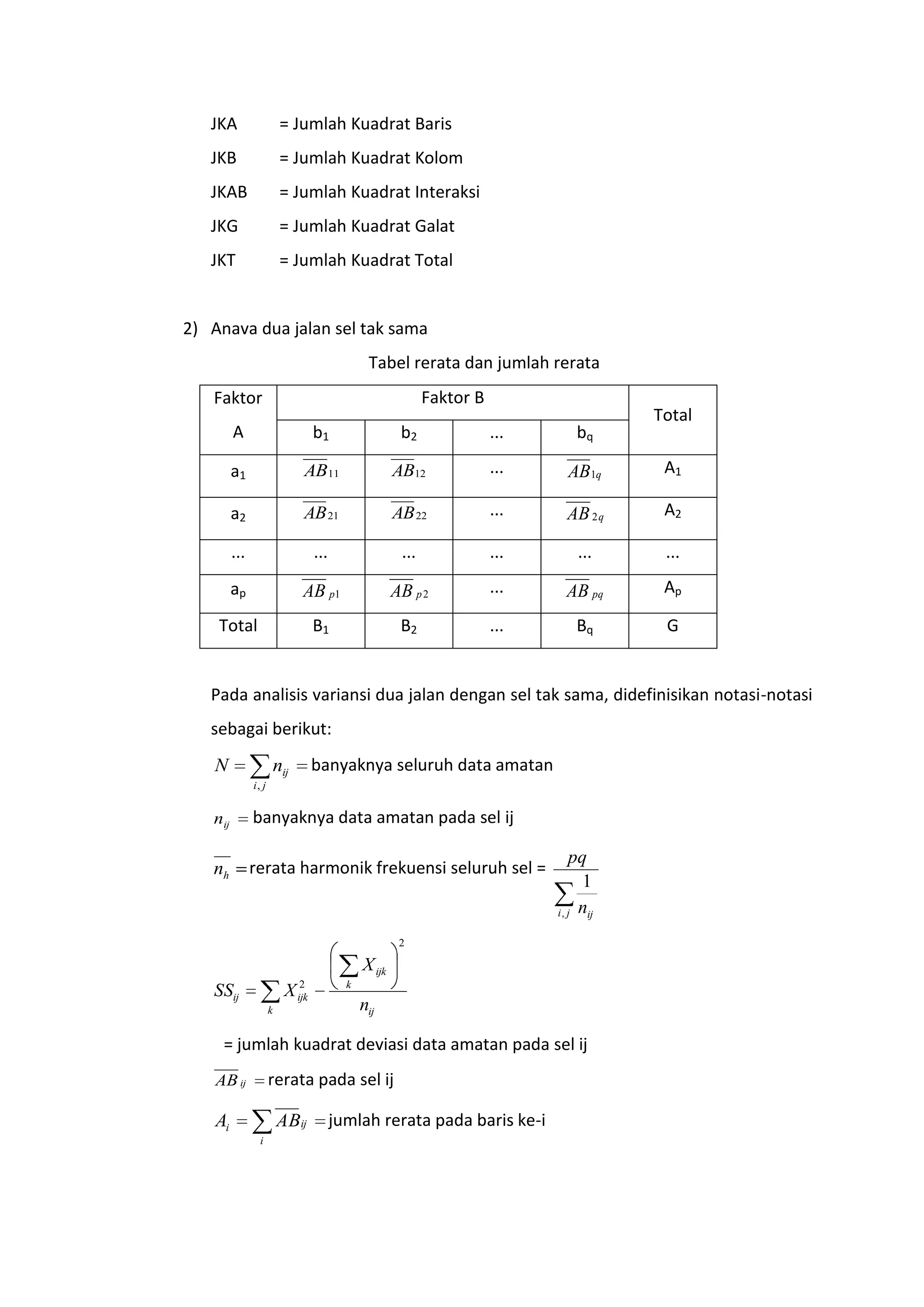
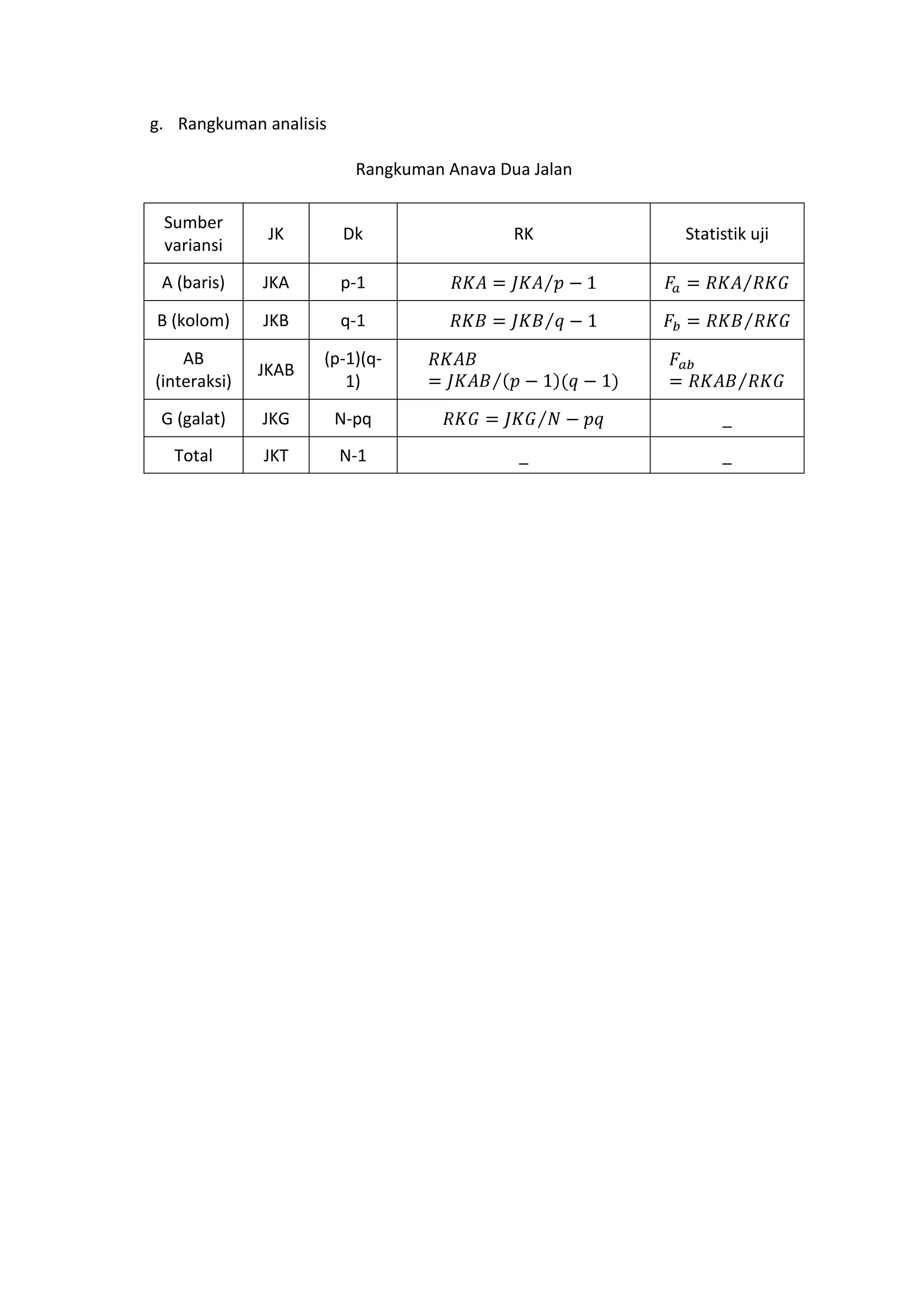
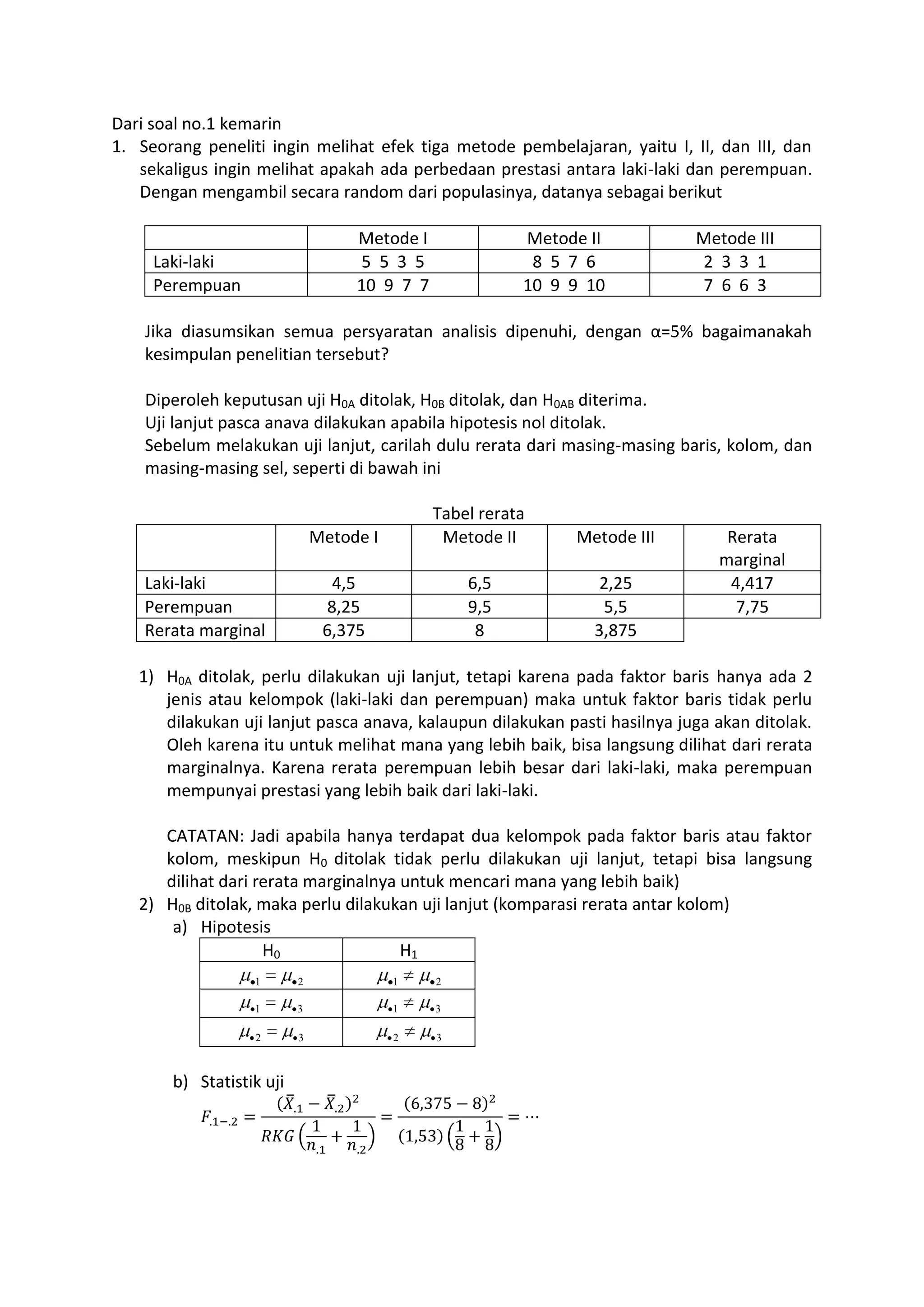
Dokumen ini membahas analisis variansi dua jalan (ANAVA) untuk menguji pengaruh dua variabel bebas terhadap satu variabel terikat dan interaksinya. Terdapat penjelasan tentang hipotesis, perhitungan jumlah kuadrat, derajat kebebasan, dan langkah-langkah dalam analisis dan uji lanjut. Contoh penelitian juga diberikan untuk menggambarkan penerapan ANAVA dalam menentukan efek metode pembelajaran dan waktu mengajar terhadap prestasi siswa.

1. ANALISIS VARIANSI DUA JALAN
Tujuan dari anava dua jalan adalah untuk menguji signifikansi efek dua variabel bebas
terhadap satu variabel terikat, dan untuk menguji signifikansi interaksi kedua variabel bebas
terhadap variabel terikat. Kedua variabel bebas tersebut disebut faktor “baris” (faktor A)
dan faktor “kolom” (faktor B).
Pada dasarnya pengujian yang pertama adalah pengujian rerata antar baris, pengujian
kedua adalah pengujian rerata antar kolom, dan pengujian ketiga adalah pengujian rerata
antar sel pada baris atau kolom yang sama.
Notasi dan Tata Letak Data
Faktor A
Faktor B
b1 b2 ... bq
a1
X111
X112
...
X11n
X121
X122
...
X12n
...
...
...
...
X1q1
X1q2
...
X1qn
a2
X211
X212
...
X21n
X221
X222
...
X22n
...
...
...
...
X2q1
X2q2
...
X2qn
... ... ... ... ...
ap
Xp11
Xp12
...
Xp1n
Xp21
Xp22
...
Xp2n
...
...
...
...
Xpq1
Xpq2
...
Xpqn
1. Hipotesis
a) H0A : αi = 0 untuk setiap i = 1, 2, 3, ..., p
H1A : paling sedikit ada satu αi yang tidak nol
b) H0B : βj = 0 untuk setiap j = 1, 2, 3, ..., q
H1B : paling sedikit ada satu βj yang tidak nol
c) H0AB : (αβ)ij = 0 untuk setiap i = 1, 2, 3, ..., p dan j = 1, 2, 3, ..., q
H1AB : paling sedikit ada satu (αβ)ij yang tidak nol
ATAU

2. a) H0A : tidak ada perbedaan efek antar baris terhadap variabel terikat
H1A : ada perbedaan efek antar baris terhadap variabel terikat
b) H0B : tidak ada perbedaan efek antar kolom terhadap variabel terikat
H1B : ada perbedaan efek antar kolom terhadap variabel terikat
c) H0AB : tidak ada interaksi antar baris dan kolom terhadap variabel terikat
H1AB : ada interaksi baris dan kolom terhadap variabel terikat
2. Komponen komputasi
a. Jumlah Kuadrat (JK)
1) Anava dua jalan sel sama
Tabel jumlah AB
Faktor
A
Faktor B
Total
b1 b2 ... bq
a1 AB11 AB12 ... AB1q A1
a2 AB21 AB22 ... AB2q A2
... ... ... ... ... ...
ap ABp1 ABp2 ... ABpq Ap
Total B1 B2 ... Bq G
Untuk memudahkan perhitungan pada anava dua jalan sel sama, didefinisikan
besaran-besaran (1), (2), (3), (4), dan (5) sebagai berikut:
N
G2
1
j
j
np
B
2
4
kji
ijkX
,,
2
2
ji
ij
n
AB
,
2
5
i
i
nq
A
2
3
)1()3(JKA
)1()4(JKB
)4()3()5()1(JKAB
)5(2JKG
JKGJKABJKBJKAJKTJKT atau)1()2(
Dimana:

3. JKA = Jumlah Kuadrat Baris
JKB = Jumlah Kuadrat Kolom
JKAB = Jumlah Kuadrat Interaksi
JKG = Jumlah Kuadrat Galat
JKT = Jumlah Kuadrat Total
2) Anava dua jalan sel tak sama
Tabel rerata dan jumlah rerata
Faktor
A
Faktor B
Total
b1 b2 ... bq
a1 11AB 12AB ... qAB1 A1
a2 21AB 22AB ... qAB2 A2
... ... ... ... ... ...
ap 1pAB 2pAB ... pqAB Ap
Total B1 B2 ... Bq G
Pada analisis variansi dua jalan dengan sel tak sama, didefinisikan notasi-notasi
sebagai berikut:
ji
ijnN
,
banyaknya seluruh data amatan
ijn banyaknya data amatan pada sel ij
hn rerata harmonik frekuensi seluruh sel =
ji ijn
pq
,
1
ij
k
ijk
k
ijkij
n
X
XSS
2
2
= jumlah kuadrat deviasi data amatan pada sel ij
ijAB rerata pada sel ij
i
iji ABA jumlah rerata pada baris ke-i

4. j
ijj ABB jumlah rerata pada kolom ke-j
ij
ijABG jumlah rerata semua sel
Untuk memudahkan perhitungan, didefinisikan besaran-besaran (1), (2), (3),
(4), dan (5) sebagai berikut:
pq
G2
1
ij
ijSS2
i
i
q
A
2
3
j
j
p
B
2
4
ij
ijAB
2
5
13hnJKA
14hnJKB
4351hnJKAB
2JKG
JKGJKABJKBJKAJKT
b. Derajat kebebasan

5. c. Rerata kuadrat
d. Statistik uji
1) Untuk adalah
2) Untuk adalah
3) Untuk adalah
e. Daerah kritik
1) Daerah kritik untuk adalah
2) Daerah kritik untuk adalah
3) Daerah kritik untuk adalah
f. Keputusan uji
1) ditolak apabila
2) ditolak apabila
3) ditolak apabila

6. g. Rangkuman analisis
Rangkuman Anava Dua Jalan
Sumber
variansi
JK Dk RK Statistik uji
A (baris) JKA p-1
B (kolom) JKB q-1
AB
(interaksi)
JKAB
(p-1)(q-
1)
G (galat) JKG N-pq _
Total JKT N-1 _ _

7. Contoh:
1. Seorang peneliti ingin melihat efek tiga metode pembelajaran, yaitu I, II, dan III, dan
sekaligus ingin melihat apakah ada perbedaan prestasi antara laki-laki dan perempuan.
Dengan mengambil secara random dari populasinya, datanya sebagai berikut
Metode I Metode II Metode III
Laki-laki 5 5 3 5 8 5 7 6 2 3 3 1
Perempuan 10 9 7 7 10 9 9 10 7 6 6 3
Jika diasumsikan semua persyaratan analisis dipenuhi, dengan α=5% bagaimanakah
kesimpulan penelitian tersebut?
2. Seorang peneliti ingin mengetahui secara serentak apakah waktu mengajar (pagi, siang,
sore) dan ukuran kelas (besar, kecil) berpengaruh terhadap prestasi belajar matematika.
Setelah satu semester, tes yang sama diberikan kepada sampel penelitian. Data
mengenai prestasi belajar disajikan dalam tabel berikut
besar kecil
Pagi 3 1 2 2 2 1 6 6 5 3 4 6
Siang 2 4 3 1 4 4 4 2 3 6 3 5
Sore 4 4 5 5 4 7 5 2 4 3 4 4
Jika diasumsikan semua persyaratan analisis dipenuhi, dengan α=5% bagaimanakah
kesimpulan penelitian tersebut?

8. UJI LANJUT PASCA ANAVA DUA JALAN DENGAN METODE SCHEFFE’
Langkah-langkah dalam menggunakan metode Scheffe’ sebagai berikut :
a. Komparasi Rerata Antar Baris
Hipotesis pada komparasi rerata antar baris adalah :
untuk setiap i = 1, 2, 3 dan j = 1,2, 3
paling tidak ada satu pasangan dan yang tidak nol
Uji Scheffe’ untuk komparasi rerata antar baris adalah :
Dengan daerah kritik :
Dengan :
= nilai pada pembandingan baris ke-i dan baris ke-j
= rerata pada baris ke-i
= rerata pada baris ke-j
RKG = rerata kuadrat galat, yang diperoleh dari perhitungan analisis variansi
= ukuran sampel baris ke-i
= ukuran sampel baris ke-j
b. Komparasi Rerata Antar Kolom
Hipotesis pada komparasi rerata antar kolom adalah :
untuk setiap i = 1, 2, 3 dan j = 1, 2, 3
paling tidak ada satu pasangan dan yang tidak nol
Uji Scheffe’ untuk komparasi rerata antar kolom adalah :
Dengan daerah kritik :
Dengan :
= nilai pada pembandingan kolom ke-i dan kolom ke-j
= rerata pada kolom ke-i
= rerata pada kolom ke-j
RKG = rerata kuadrat galat, yang diperoleh dari perhitungan analisis variansi
= ukuran sampel kolom ke-i
= ukuran sampel kolom ke-j

9. c. Komparasi Rerata Antar Sel pada Kolom yang Sama
Hipotesis pada komparasi rerata antar sel pada kolom yang sama adalah :
untuk setiap i = 1, 2, ..., k dan j = 1, 2, 3
paling tidak ada satu pasang dan yang tidak nol
Uji Scheffe’ untuk komparasi rerata antar sel pada kolom yang sama adalah sebagai
berikut:
kjij
kjij
kjij
nn
RKG
XX
F
11
2
Dengan:
kjijF = nilai obsF pada pembandingan rerata pada sel ij dan ik.
ijX = rerata pada sel ij
kjX = rerata pada sel ik
RKG = rerata kuadrat galat yang diperoleh dari perhitungan analisis variansi
ijn = ukuran sel ij
kjn = kuran sel ik
Sedangkan daerah kritik untuk uji itu adalah :
d. Komparasi Rerata Antar Sel pada Baris yang Sama
Hipotesis pada komparasi rerata antar sel pada baris yang sama adalah
untuk setiap i = 1, 2, 3 dan j = 1, 2, ..., k
paling tidak ada satu pasang dan yang tidak nol
Uji Scheffe’ untuk komparasi rerata antar sel pada baris yang sama adalah sebagai
berikut :
ikij
ikij
ikij
nn
RKG
XX
F
11
2
Sedangkan daerah kritik untuk uji itu adalah :

10. Dari soal no.1 kemarin
1. Seorang peneliti ingin melihat efek tiga metode pembelajaran, yaitu I, II, dan III, dan
sekaligus ingin melihat apakah ada perbedaan prestasi antara laki-laki dan perempuan.
Dengan mengambil secara random dari populasinya, datanya sebagai berikut
Metode I Metode II Metode III
Laki-laki 5 5 3 5 8 5 7 6 2 3 3 1
Perempuan 10 9 7 7 10 9 9 10 7 6 6 3
Jika diasumsikan semua persyaratan analisis dipenuhi, dengan α=5% bagaimanakah
kesimpulan penelitian tersebut?
Diperoleh keputusan uji H0A ditolak, H0B ditolak, dan H0AB diterima.
Uji lanjut pasca anava dilakukan apabila hipotesis nol ditolak.
Sebelum melakukan uji lanjut, carilah dulu rerata dari masing-masing baris, kolom, dan
masing-masing sel, seperti di bawah ini
Tabel rerata
Metode I Metode II Metode III Rerata
marginal
Laki-laki 4,5 6,5 2,25 4,417
Perempuan 8,25 9,5 5,5 7,75
Rerata marginal 6,375 8 3,875
1) H0A ditolak, perlu dilakukan uji lanjut, tetapi karena pada faktor baris hanya ada 2
jenis atau kelompok (laki-laki dan perempuan) maka untuk faktor baris tidak perlu
dilakukan uji lanjut pasca anava, kalaupun dilakukan pasti hasilnya juga akan ditolak.
Oleh karena itu untuk melihat mana yang lebih baik, bisa langsung dilihat dari rerata
marginalnya. Karena rerata perempuan lebih besar dari laki-laki, maka perempuan
mempunyai prestasi yang lebih baik dari laki-laki.
CATATAN: Jadi apabila hanya terdapat dua kelompok pada faktor baris atau faktor
kolom, meskipun H0 ditolak tidak perlu dilakukan uji lanjut, tetapi bisa langsung
dilihat dari rerata marginalnya untuk mencari mana yang lebih baik)
2) H0B ditolak, maka perlu dilakukan uji lanjut (komparasi rerata antar kolom)
a) Hipotesis
H0 H1
21 21
31 31
32 32
b) Statistik uji

11. Silahkan dilanjutkan sendiri!!!
c) Daerah kritis
...
d) Keputusan uji
e) Kesimpulan
(karena ada tiga hipotesis, maka keputusan uji dan kesimpulan juga ada tiga)
2. Seorang peneliti ingin mengetahui secara serentak apakah waktu mengajar (pagi, siang,
sore) dan ukuran kelas (besar, kecil) berpengaruh terhadap prestasi belajar matematika.
Setelah satu semester, tes yang sama diberikan kepada sampel penelitian. Data
mengenai prestasi belajar disajikan dalam tabel berikut
besar kecil
Pagi 3 1 2 2 2 1 6 6 5 3 4 6
Siang 2 4 3 1 4 4 4 2 3 6 3 5
Sore 4 4 5 5 4 7 5 2 4 3 4 4
Jika diasumsikan semua persyaratan analisis dipenuhi, dengan α=5% bagaimanakah
kesimpulan penelitian tersebut?
Keputusan uji: H0A diterima, H0B ditolak, dan H0AB ditolak.
Tabel rerata
Besar Kecil Rerata
marginal
Pagi ... ... ...
Siang ... ... ...
Sore ... ... ...
Rerata marginal ... ...
1) H0B ditolak, perlu dilakukan uji lanjut, tetapi karena pada faktor kolom hanya ada 2
jenis atau kelompok (besar dan kecil) maka untuk faktor kolom tidak perlu
dilakukan uji lanjut pasca anava, kalaupun dilakukan pasti hasilnya juga akan
ditolak. Oleh karena itu untuk melihat mana yang lebih baik, bisa langsung dilihat
dari rerata marginalnya. Karena rerata ... lebih besar dari ..., maka ... mempunyai
efek yang lebih baik dari ...
2) H0AB ditolak, maka perlu dilakukan uji lanjut (kkomparasi rerata antar sel pada baris
atau kolom yang sama)
a) Hipotesis

12. H0 H1
1211 1211
2221 2221
3231 3231
2111 2111
3111 3111
3121 3121
2212 2212
3212 3212
3222 3222
b) Statistik uji
dst
c) Daerah kritis
d) Keputusan uji
e) Kesimpulan
(silahkan dilanjutkan sendiri)

13. TUGAS ( dikumpulkan hari ini juga)
Seorang peneliti ingin mengetahui manakah metode pembelajaran yang paling efektif
diantara CTL dan NHT. Peneliti tersebut juga ingin mengetahui manakah yang lebih efektif
antara waktu pelaksanaan pembelajaran pagi, siang, dan sore. Selain itu peneliti juga ingin
mengetahui apakah terdapat perbedaan prestasi belajar siswa yang mengikuti
pembelajaran dengan CTL dan NHT pada tiap-tiap waktu pelaksanaan pembelajaran. Setelah
dilakukan eksperimen dan diambil sampel dari populasinya, datanya disajikan dalam tabel
berikut
Pagi Siang Sore
CTL 8 9 8 7 6 6 7 5 5 4 4 3
NHT 8 9 9 6 7 9 8 8 3 3 4 2
Jika diasumsikan semua persyaratan analisis dipenuhi,
a. Dengan tingkat signifikansi 5%, bagaimanakah kesimpulan dari penelitian tersebut?
b. Apakah anda perlu melakukan uji lanjut pasca anava? Kalau perlu lakukanlah dan
bagaimana kesimpulannya?