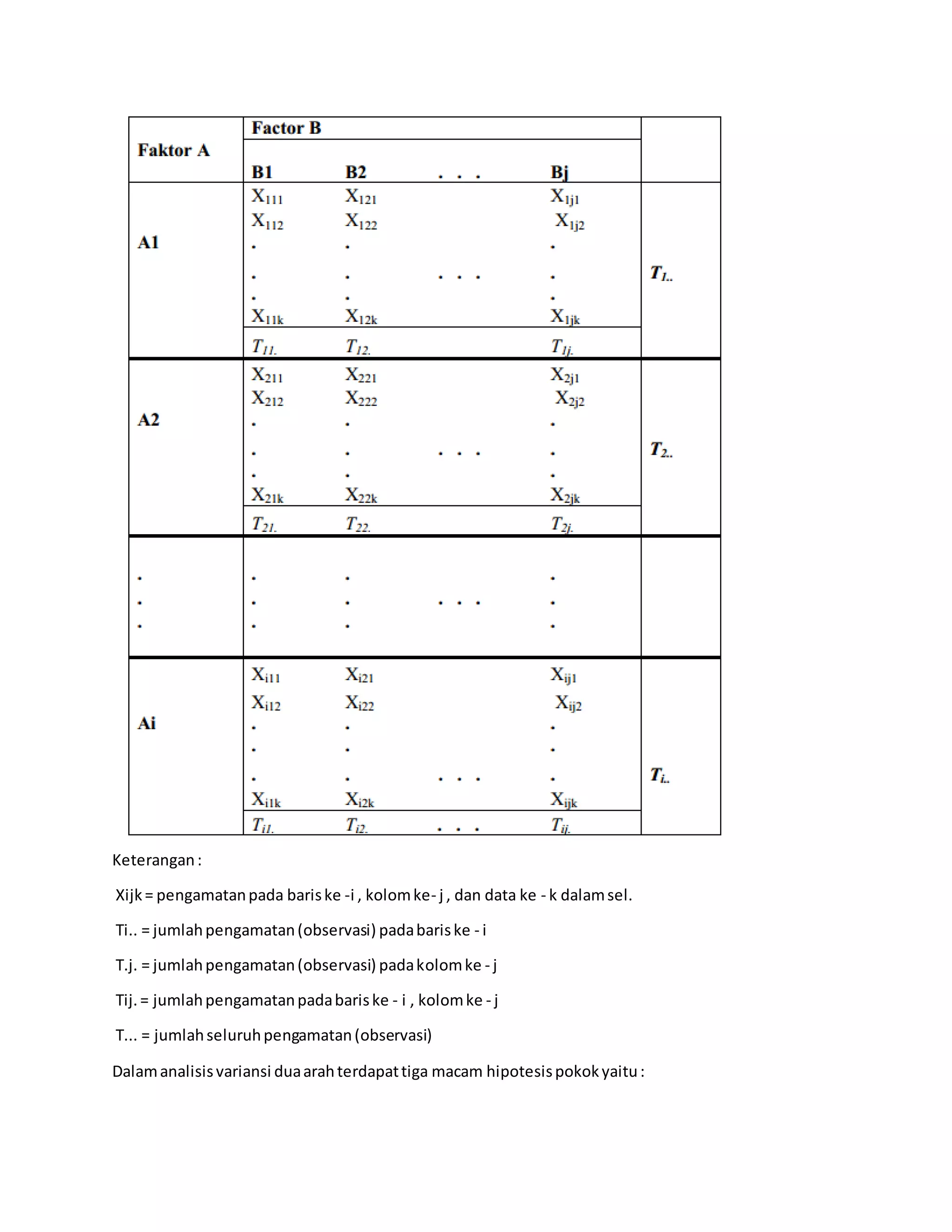
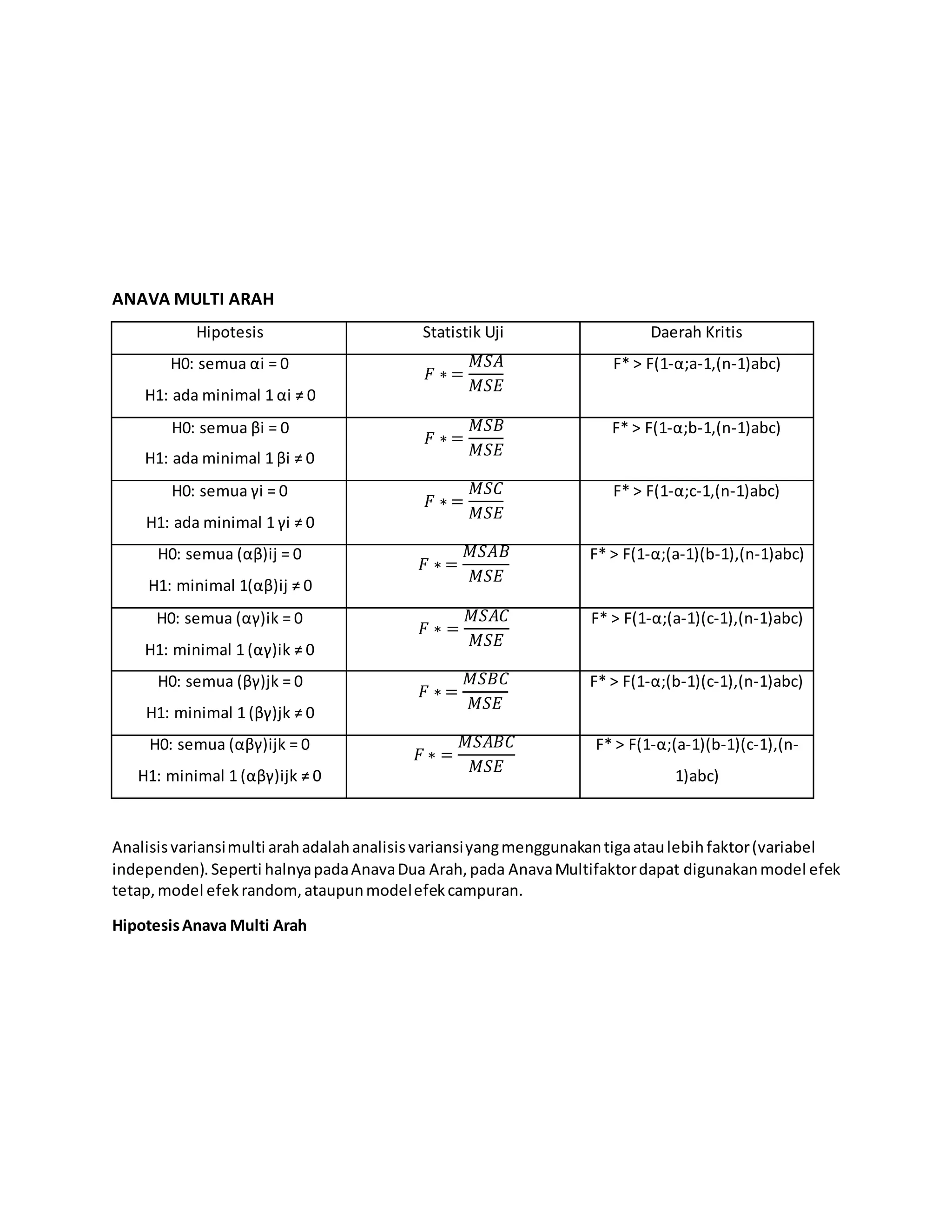
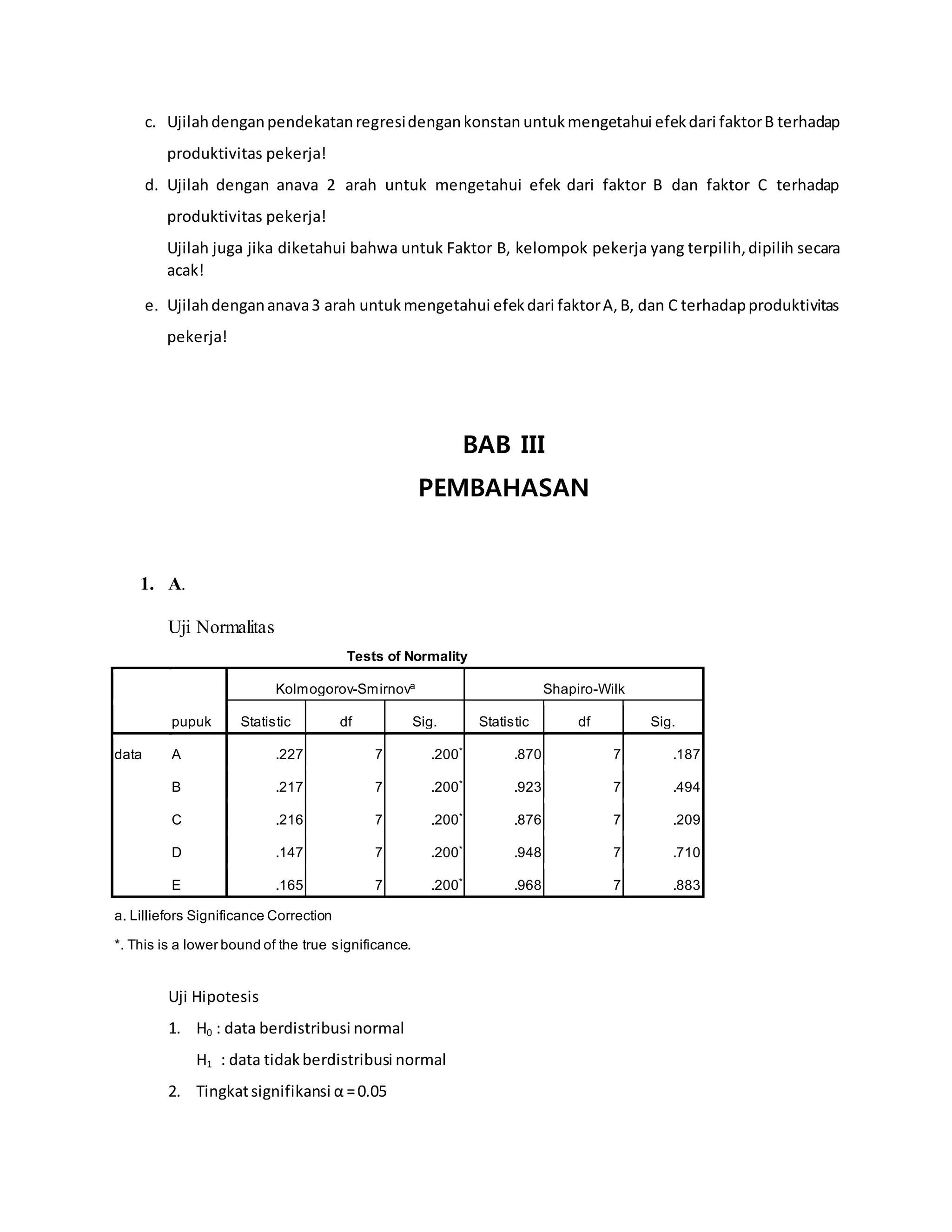
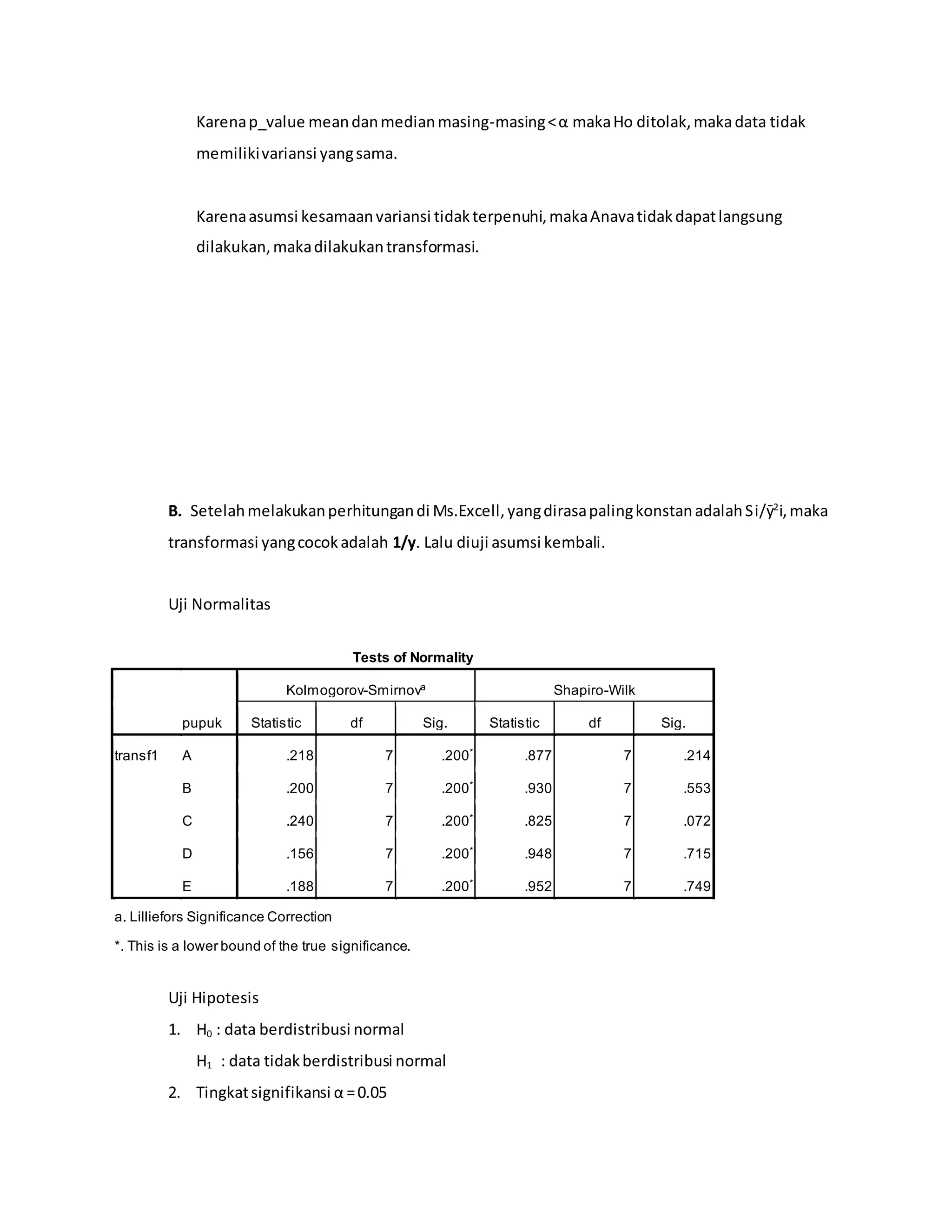
Laporan ini membahas praktikum analisis variansi terapan. Terdapat beberapa bab yang membahas landasan teori ANOVA satu arah dan dua arah beserta contoh soal dan penyelesaiannya. Soal uji kasus menguji pengaruh jenis pupuk terhadap hasil panen gabah dan pengaruh faktor shift kerja, kelompok pekerja dan jenis kelamin terhadap produktivitas pekerja.

1. LAPORAN
PRAKTIKUM ANALISIS VARIANSI
TERAPAN
Dosen Pengampu :
Prof. Dr. Sri Haryatmi Kartiko, M.Si
Asisten Praktikum :
Yulia Indah
Muhammad Fuad Hasyim
Oleh :
Adhitya Akbar
10/297716/PA/13065
LABORATORIUM KOMPUTASI
MATEMATIKA DAN STATISTIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

2. UNIVERSITAS GADJAH MADA
YOGYAKARTA
2013
BAB I
LANDASAN TEORI
Analisisvarians (analysisofvariance,ANOVA) adalah suatu metode analisisstatistikayangtermasukke
dalam cabang statistika inferensi. Dalam literatur Indonesia metode ini dikenal dengan berbagai nama
lain,sepertianalisisragam, sidikragam,dan analisisvariansi.Iamerupakanpengembangandari masalah
Behrens-Fisher, sehingga uji-F juga dipakai dalam pengambilan keputusan. Analisis varians pertama kali
diperkenalkan oleh Sir Ronald Fisher, bapak statistika modern. Dalam praktik, analisis varians dapat
merupakan uji hipotesis (lebih sering dipakai) maupun pendugaan (estimation, khususnya di bidang
genetika terapan).
Secara umum,analisisvariansmenguji dua varians(atauragam) berdasarkan hipotesis nol bahwakedua
variansitusama.Varianspertamaadalahvariansantarcontoh(amongsamples)danvarianskeduaadalah
variansdi dalammasing-masingcontoh(within samples).Denganidesemacamini,analisisvariansdengan
dua contoh akan memberikan hasil yang sama dengan uji-t untuk dua rerata (mean).
Supaya sahih (valid) dalam menafsirkan hasilnya, analisis varians menggantungkan diri pada empat
asumsi yang harus dipenuhi dalam perancangan percobaan:
1. Data berdistribusi normal,karenapengujiannyamenggunakanuji F-Snedecor
2. Variansatau ragamnyahomogen,dikenalsebagai homoskedastisitas,karenahanyadigunakan
satu penduga(estimate) untukvariansdalamcontoh
3. Masing-masingcontohsalingbebas,yangharusdapatdiaturdenganperancanganpercobaan
yang tepat
4. Komponen-komponendalammodelnyabersifataditif (salingmenjumlah).

3. Uji mean yang dilakukan untuk k populasi ( k > 2 ), memerlukan prosedur yang agak sedikit berbeda
dengan 1 atau 2 populasi. Jika t-test atau z-test digunakan untuk menganalisis data 1 atau 2 populasi,
tetapi tidakcukupbaikuntukkasuslebihdari 2populasi (k>2).Hal ini disebabkankarenajikaadasejumlah
k populasi,berarti akanada pasanganmeanyang akan diuji.Misalkanada4 populasi A,B,C dan D untuk
mengetahui apakah terdapat perbedaan berarti diantara populasi tersebut, kita harus menguji apakah
ada perbedaan antara pasangan AB, AC, AD, BC, BD, dan CD. Berarti untuk kasus ini diperlukan 6 uji-t
yang terpisah.Hal ini sangat tidakefektif danakanmenimbulkangalatseluruhnyamenjaditerlalu besar.
Olehkarenaitudiperlukansuatumetode yangtepatuntukmengatasi masalahtersebut,yaitudigunakan
uji statistika yang disebut Analisis Variansi (ANAVA).
ASUMSIDALAM ANOVA
Ada beberapaasumsi yangharusdipenuhi olehdatadalamanalisisvariansiini,seperti
yang telahdijelaskanpadababsebelumnyayaitu:
1. Data bersifatindependen
2. Data berdistribusi normal
3. Data mempunyai variansiyangrelatif sama
Jikaasumsi di atas tidakterpenuhi,makaadaprosedurkhususyangharusdilakukan.
Misalnya,datayang dianalisistidakmengikutidistribusinormal.Penangananyangdapat dilakukanuntuk
masalah tersebut salah satunya adalah dengan mentransformasi data. Selain dengantransformasi data,
cara lain untuk menganalisis data tersebut adalah dengan
melakukan uji non parametrik dimana uji tersebut tidak membutuhkan asumsi-asumsi seperti pada uji
parametrik.Uji nonparametrikyangdapatdilakukanmisalnya:uji Mann-Whitney, Wilcoxonsigned-rank
test, Sign test, Kruskal Wallis, dll.
ANAVA SATU ARAH
Anava satu arah adalah analisis variansi yang hanya menggunakan satu variabel independen.
TujuanANAVA SatuArah:
o Untuk membandingkanrata-rata(mean) dari beberapapopulasi (lebihdari dua).
o Untuk melihatefeksuatufaktorterhadapvariabel dependen.

4. Partisi Variansi
Variansi total dapatdibagi menjadi 2bagian:
SST = SSG + SSW
SST = Total sum of squares (jumlahkuadrattotal) yaitupenyebaranagregatnilai dataindividumelalui
beberapalevel faktor.
SSG/SSB= Sumof squaresbetween-grup(Jumlahkuadratantara) yaitupenyebarandiantaramean
sampel faktor.
SSW/SSE= Sumof squareswithin-grup(jumlahkuadratdalam) yaitupenyebaranyangterdapatdiantara
nilai datadalamsebuahlevel faktortertentu.
Rumusjumlahkuadarattotal ( total sum of squares)
Keterangan :
SSW/SSE = jumlah kuadrat dalam
k = levels of treatment ( jumlah populasi )
ni = ukuran sampel dari poplasi i

5. xij = pengukuran ke-j dari populsi ke-i
x = mean keseluruha ( dari seluruh nilai data )
Rumus untuk mencari varisi diantara grup
Keterangan :
SSB/SSG = jumlah kuadrat diantara
k = levels of treatment ( jumlah populasi )
ni = ukuran sampel dari poplasi i
xij = pengukuran ke-j dari populsi ke-i
x = mean keseluruha ( dari seluruh nilai data )
Rumus variasi dalam kelompok
MSW =SSW/N-K
dimana:
MSW = Rata-rata variasi dalam kelompok
SSW = jumlah kuadrat dalam
N-K = derajat bebas dari SSW
rumus variasi diantara kelompok
MSG = SSG/K-1
MSG/SSW = Rata-rata variasi diantara kelompok
SSG = jumlah kuadrat antara
k-1 = derajat bebas SSG
PROSEDUR UJI HIPOTESIS DALAM ANAVASATU ARAH
1. Ho : µ1 = µ2 =.....= µn

6. H1 : tidaksemuaµi sama
2. Tingkatsignifikansi α =0.05
3. StatistikUji
𝐹 =
𝑀𝑆𝑇
𝑀𝑆𝐸
~𝐹𝑘 − 1; 𝑁 − 𝑘 atau sig(p-value)
4. Daerah kritik
Ho ditolakjikap-value <α
ANALISIS PERBANDINGANGANDA( Multiple Comparison Analysis(MCA) )
 JikadalamANAVA H0 tidakditolak,makapekerjaanselesai dengankesimpulansemua
rata-rata relatif sama.
 JikadalamANAVA H0 ditolak,makamasihadapekerjaanuntukmelihatrata-rata
populasi manayangbenar-benarberbedadenganmenggunakanMCA.
 syarat MCA = jumlahlevelfaktornya(perlakuan) lebihdari dua.
Macam-macam metode yangdapatdigunakanuntukanalisisini adalahsbb:
o Tukey: untukukuransampel yangsama pada setiapperlakuan(equal )
o Bonferroni :untukukuransampel yangsama dan bedapadasetiapperlakuan
(equal&unequal)
o Scheffe :untukukuransampel yangsama danbeda padasetiapperlakuan(equal&
unequal)
o Fisher(LSD= LeastSquare Differences) :yangpaling umumdigunakan

7. ANALISIS VARIANSI DUA ARAH
AnalisisVariansi dapatdiperluasuntukpermasalahan/kasusyangmelibatkandua faktor.
Analisisvariansi2arah bertujuanuntukmengetahuiadatidaknyaefekatau pengaruhdari duafaktor.
Dalamanalisisini dapatdilakukanuji hipotesistentang perbedaanantarlevel faktordalamvariabelA
ataupundalamvariabel B.Jikaobservasi untuksetiapkombinasi level faktorlebihdari satu,dapatjuga
dilakukanuji hipotesisuntukmeanpopulasiinteraksi antarafaktorA dan faktorB.
Desaindatadapat dilihatseperti bawahini :

8. Keterangan:
Xijk= pengamatanpada bariske -i , kolomke- j , dan data ke - k dalamsel.
Ti.. = jumlahpengamatan(observasi) padabariske - i
T.j. = jumlahpengamatan(observasi) padakolomke - j
Tij.= jumlahpengamatanpadabariske - i , kolomke - j
T... = jumlahseluruhpengamatan(observasi)
Dalamanalisisvariansi duaarahterdapattiga macam hipotesispokokyaitu:

9. efekinteraksi menyelidikiapakahadapengaruhkombinasi antarafaktorA dan B. Untuk
menguji efekinteraksi ini diperlukanadanyareplikasi(ulangan) percobaanpadasetiap
sel.Jikadatayang tersediapadatiapsel hanyaada satu saja,maka efekini tidakdapat
diukur.
Langkah-langkahuji hipotesisyangdigunakanadalahsebagai berikut:

10. Tabel ANOVADUA ARAH
Uji hipotesispadaanovadua arah ini masihrelatif sesederhanaseperti padaanovasatu
arah. Secara lengkapuji hipotesisnyadapatdilihatpadatabel anovadi bawahini :

11. Kuantitas-kuantitasdi atasdijelaskandalamtabel di bawah:

12. ANAVA MULTI ARAH
Analisisvariansimulti arahadalahanalisisvariansiyangmenggunakantigaataulebihfaktor(variabel
independen).Seperti halnyapadaAnavaDua Arah,pada AnavaMultifaktordapat digunakanmodel efek
tetap,model efekrandom,ataupunmodelefekcampuran.
HipotesisAnava Multi Arah
Hipotesis Statistik Uji Daerah Kritis
H0: semua αi = 0
H1: ada minimal 1 αi ≠ 0
𝐹 ∗ =
𝑀𝑆𝐴
𝑀𝑆𝐸
F* > F(1-α;a-1,(n-1)abc)
H0: semua βi = 0
H1: ada minimal 1 βi ≠ 0
𝐹 ∗ =
𝑀𝑆𝐵
𝑀𝑆𝐸
F* > F(1-α;b-1,(n-1)abc)
H0: semua γi = 0
H1: ada minimal 1 γi ≠ 0
𝐹 ∗ =
𝑀𝑆𝐶
𝑀𝑆𝐸
F* > F(1-α;c-1,(n-1)abc)
H0: semua (αβ)ij = 0
H1: minimal 1(αβ)ij ≠ 0
𝐹 ∗ =
𝑀𝑆𝐴𝐵
𝑀𝑆𝐸
F* > F(1-α;(a-1)(b-1),(n-1)abc)
H0: semua (αγ)ik = 0
H1: minimal 1 (αγ)ik ≠ 0
𝐹 ∗ =
𝑀𝑆𝐴𝐶
𝑀𝑆𝐸
F* > F(1-α;(a-1)(c-1),(n-1)abc)
H0: semua (βγ)jk = 0
H1: minimal 1 (βγ)jk ≠ 0
𝐹 ∗ =
𝑀𝑆𝐵𝐶
𝑀𝑆𝐸
F* > F(1-α;(b-1)(c-1),(n-1)abc)
H0: semua (αβγ)ijk = 0
H1: minimal 1 (αβγ)ijk ≠ 0
𝐹 ∗ =
𝑀𝑆𝐴𝐵𝐶
𝑀𝑆𝐸
F* > F(1-α;(a-1)(b-1)(c-1),(n-
1)abc)

13. BAB II
PERMASALAHAN
1. Berikut ini adalah banyaknya panen gabah di suatu daerah menggunakan pupuk yang berbeda
:
A B C D E
76 75 77 69 59
79 85 83 63 51
88 79 84 68 49
75 88 82 65 54
90 80 64 65 55
80 89 66 60 56
91 78 50 61 57
Dari data tersebut,
a. Ujilah apakah asumsi kenormalan dan kesamaan variansi dalam anava terpenuhi!
b. Jika asumsi pada soal no.1a tidak terpenuhi, transformasi apakah yang paling cocok untuk
menstabilkan variansi / mendekatkan data tersebut dalam distribusi normal? (jika asumsi
terpenuhi, langsung kerjakan soal no.1c).
c. Ujilah apakah kelima jenis pupuk mempunyai jumlah panen yang sama!
d. Jika ada nilai yang tidak sama, jenis pupuk mana yang berbeda?
e. Jika pupuk A,B dan C termasuk pupuk buatan, D dan E termasuk pupuk alami, apakah
kesimpulan Anda tentang kedua pupuk tersebut!
f. Lakukan pendekatan regresi untuk anava dengan menggunakan konstan dan tanpa
konstan? Bagaimana kesimpulannya?

14. 2. Apakah yang Anda ketahui tentang uji Krukal Wallis?Padakondisi seperti apa ujiKruskal Wallis
digunakan?
Statistik uji apakah yang sering digunakan dalam analisis variansi? Mengapa digunakan
statistik uji tersebut?
3. Ingin diteliti apakah produktivitas pekerja di pabrik XYZ dipengaruhi oleh shift kerja, kelompok
pekerja dan jenis kelamin. Dari total 5000 pekerja yang semuanya terbagi ke dalam 20
kelompok kerja, hanya diteliti 40 pekerja dari 5 kelompok pekerja.
Factor A : jenis kelamin
Factor B : Kelompok pekerja
Factor C : Shift kerja
Shift1 Shift2 Shift3 Shift4
00.00-06.00 06.00-12.00 12.00-18.00 18.00-24.00
Laki-Laki
KelompokA 59 82 78 54
KelompokB 90 98 72 77
KelompokC 84 62 71 81
KelompokD 78 62 75 90
KelompokE 80 96 86 65
Perempuan
KelompokA 53 88 90 63
KelompokB 80 93 63 97
KelompokC 71 80 74 82
KelompokD 71 60 67 79
KelompokE 96 91 92 81
a. Ujilah asumsi kenormalan dan kesamaan variansi pada data diatas!
b. JikauntukfaktorB kelompokA,BmerupakanparapekerjadenganlatarbelakangpendidikanSMK
, kelompok C,D merupakan para pekerja berpendidikan D3 dan kelompok E merupakan para
pekerja berpendidikan S1, apakah ada perbedaan produktivitas pekerja?

15. c. Ujilahdenganpendekatanregresidengankonstan untukmengetahui efekdari faktorB terhadap
produktivitas pekerja!
d. Ujilah dengan anava 2 arah untuk mengetahui efek dari faktor B dan faktor C terhadap
produktivitas pekerja!
Ujilah juga jika diketahui bahwa untuk Faktor B, kelompok pekerja yang terpilih,dipilih secara
acak!
e. Ujilahdengananava3 arah untukmengetahui efekdari faktorA,B, dan C terhadapproduktivitas
pekerja!
BAB III
PEMBAHASAN
1. A.
Uji Normalitas
Tests of Normality
pupuk
Kolmogorov-Smirnova Shapiro-Wilk
Statistic df Sig. Statistic df Sig.
data A .227 7 .200*
.870 7 .187
B .217 7 .200* .923 7 .494
C .216 7 .200*
.876 7 .209
D .147 7 .200* .948 7 .710
E .165 7 .200*
.968 7 .883
a. Lilliefors Significance Correction
*. This is a lower bound of the true significance.
Uji Hipotesis
1. H0 : data berdistribusi normal
H1 : data tidakberdistribusi normal
2. Tingkatsignifikansi α =0.05

16. 3. StatistikUji (Kolmogorov-Smirnov)
p-value A = 0.200
p-value B= 0.200
p-value C= 0.200
p-value D= 0.200
p-value E= 0.200
4. Daerah kritik
Ho ditolakjikap-value <α
5. Kesimpulan
Karenasemuap_value > α makaHo tidakditolakuntukseluruhHo,maka databerdistribusi
normal
Uji KesamaanVariansi
Test of Homogeneity of Variance
Levene Statistic df1 df2 Sig.
data Based on Mean 7.648 4 30 .000
Based on Median 2.791 4 30 .044
Based on Median and with
adjusted df
2.791 4 12.667 .072
Based on trimmed mean 7.118 4 30 .000
Uji Hipotesis
1. Ho : σ²1 = σ²2 = σ²3 = σ²4 (databervariansi sama)
H1 : tidaksemuaσi² sama ( data tidakbervariansi sama)
2. Tingkatsignifikansi α =0.05
3. StatistikUji
p-value mean=0.000
p-value median=0.044
4. Daerah kritik
Ho ditolakjikap-value <α
5. Kesimpulan

17. Karenap_value meandanmedianmasing-masing<α makaHo ditolak,makadata tidak
memilikivariansi yangsama.
Karenaasumsi kesamaanvariansi tidakterpenuhi,makaAnavatidakdapatlangsung
dilakukan,makadilakukantransformasi.
B. Setelahmelakukanperhitungandi Ms.Excell,yangdirasapalingkonstanadalahSi/ȳ2
i,maka
transformasi yangcocokadalah 1/y. Lalu diuji asumsi kembali.
Uji Normalitas
Tests of Normality
pupuk
Kolmogorov-Smirnova
Shapiro-Wilk
Statistic df Sig. Statistic df Sig.
transf1 A .218 7 .200*
.877 7 .214
B .200 7 .200*
.930 7 .553
C .240 7 .200*
.825 7 .072
D .156 7 .200*
.948 7 .715
E .188 7 .200*
.952 7 .749
a. Lilliefors Significance Correction
*. This is a lower bound of the true significance.
Uji Hipotesis
1. H0 : data berdistribusi normal
H1 : data tidakberdistribusi normal
2. Tingkatsignifikansi α =0.05

18. 3. StatistikUji (Kolmogorov-Smirnov)
p-value A = 0.200
p-value B= 0.200
p-value C= 0.200
p-value D= 0.200
p-value E= 0.200
4. Daerah kritik
Ho ditolakjikap-value <α
5. Kesimpulan
Karenasemuap_value > α makaHo tidakditolakuntukseluruhHo,makadataberdistribusi
normal
Uji KesamaanVariansi
Test of Homogeneity of Variance
Levene Statistic df1 df2 Sig.
transf1 Based on Mean 4.678 4 30 .005
Based on Median 1.912 4 30 .134
Based on Median and with
adjusted df
1.912 4 9.349 .190
Based on trimmed mean 4.286 4 30 .007
Uji Hipotesis
1. Ho : σ²1 = σ²2 = σ²3 = σ²4 (databervariansi sama)
H1 : tidaksemuaσi² sama ( data tidakbervariansi sama)
2. Tingkatsignifikansi α =0.05
3. StatistikUji
p-value mean=0.005
p-value median=0.134
4. Daerah kritik
Ho ditolakjikap-value <α
5. Kesimpulan

19. Walaupun p_value meanmasihkurangdari α,tetapi p_value mediansudah>α maka Ho
tidakditolak untukmedian,makadatamemiliki variansiyangsamaberdasarkanmedian.
Jikadibandingkandenganuji kesamaanvariansiyangdilakukanpadadatatransformasi lnydibawahini,
maka hasil uji kesamaanvariansi hasil transformasi 1/y diatasmasihlebihbaik.
Test of Homogeneity of Variance
Levene Statistic df1 df2 Sig.
transf2 Based on Mean 5.867 4 30 .001
Based on Median 2.271 4 30 .085
Based on Median and with
adjusted df
2.271 4 10.452 .131
Based on trimmed mean 5.409 4 30 .002
C.
ANOVA
transf1
Sum of Squares df Mean Square F Sig.
Between Groups .000 4 .000 19.297 .000
Within Groups .000 30 .000
Total .000 34
Uji Hipotesis
5. Ho : µ1 = µ2 =.....= µn
H1 : tidaksemuaµi sama
6. Tingkatsignifikansi α =0.05
7. StatistikUji
p-value =0.000
8. Daerah kritik
Ho ditolakjikap-value <α
9. Kesimpulan

20. Karenap_value (0.000) < α (0.05) makaHo ditolak.,sehinggatidaksemuaµi samaatau
dengankata lainpalingtidakadasatu jenisdari keempatjenispupukyangmemberikanhasil
produksi yangberbeda.
D.
transf1
Tukey HSDa
pupuk N
Subset for alpha = 0.05
1 2 3
A 7 .0122
B 7 .0122
C 7 .0143 .0143
D 7 .0156
E 7 .0184
Sig. .114 .553 1.000
Means for groups in homogeneous subsets are displayed.
a. Uses Harmonic Mean Sample Size = 7,000.
Dilihatdari rata-ratanya(0.0184), maka pupukE-lahyangberbeda(memberikanhasil produksi terbesar).
E.

21. Contrast Coefficients
Contras
t
pupuk
A B C D E
1 1 1 1 -1.5 -1.5
Contrast Tests
ContrastValue of Contrast Std. Error t df Sig. (2-tailed)
data Assume equal variances 1 58.7143 7.46488 7.865 30 .000
Does notassume equal
variances
1 58.7143 6.42645 9.136 16.378 .000
Uji Hipotesis
1. Ho : L = 0
H1 : L ≠ 0
2. Tingkatsignifikansi α =0.05
3. StatistikUji
p-value =0.000
4. Daerah kritik
Ho ditolakjikap-value <α
5. Kesimpulan
Karenap_value kontras(0.000) < α (0.05) maka Ho ditolak.,sehinggaantara pupuk
buatan(A,B,C) danpupukalami(D,E) berbedasecarasignifikan.
Jika pupuk A, B, C pupuk buatan dan pupuk D, E adalah pupuk alami, maka pupuk alami lebih
baik dari pada pupuk buatan(pupuk alami memberikan hasil produksi yang lebih besar), dapat
dilihat di tabel hasil tes Tukey(MCA) di atas pada jawaban poin D.
F.

22. o Dengankonstanta
ANOVAb
Model Sum of Squares df Mean Square F Sig.
1 Regression 4042.686 4 1010.671 19.432 .000a
Residual 1560.286 30 52.010
Total 5602.971 34
a. Predictors:(Constant),X4, X3, X2, X1
b. DependentVariable:data
Uji Hipotesis
1. Ho : τ1 = τ2 =....= τa-1 = 0
H1 : tidaksemuaτ1 = 0 ; i=1,2,....,a-1
2. Tingkatsignifikansi α =0.05
3. Statistik Uji
p-value =0.000
4. Daerah kritik
Ho ditolakjikap-value <α
5. Kesimpulan
Karenap-value (0.000) < α (0.05) maka Ho ditolak,sehinggakelimajenispupukmemberikan
hasil produksi yangberbeda.
o Tanpa konstanta

23. ANOVAc,d
Model Sum of Squares df Mean Square F Sig.
1 Regression 181330.714 5 36266.143 697.298 .000a
Residual 1560.286 30 52.010
Total 182891.000b
35
a. Predictors:X5, X4, X3, X2, X1
b. This total sum of squares is notcorrected for the constantbecause the constantis zero for
regression through the origin.
c. DependentVariable:data
d. Linear Regression through the Origin
Uji Hipotesis
1. Ho : τ1 = τ2 =....= τa-1 = 0
H1 : tidaksemuaτ1 = 0 ; i=1,2,....,a-1
2. Tingkatsignifikansi α =0.05
3. StatistikUji
p-value =0.000
4. Daerah kritik
Ho ditolakjikap-value <α
5. Kesimpulan
Karenap-value (0.000) < α (0.05) maka Ho ditolak,sehinggakelimajenispupukmemberikan
hasil produksi yangberbeda.
Kesimpulan:Perhitungandengandantanpakonstantamemberikan hasil/kesimpulanyang
sama, yaitukelimajenispupukmemberikanhasil produksi yangberbeda.
2. Uji Kruskal-Wallisadalahujinonparametrikyangdigunakanuntukmembandingkantigaataulebih
kelompok data sampel. Uji Kruskal-Wallis digunakan ketika asumsi ANOVA tidak terpenuhi.
Pada ANOVA, kita asumsikan bahwa distribusi dari masing-masing kelompok harus terdistribusi
secara normal. Dalam uji Kruskal-Wallis, tidak diperlukan asumsi tersebut, sehingga uji Kruskal-
Wallisadalahuji distribusi bebas.Jikaasumsi normalitasterpenuhi,makauji Kruskal-Wallistidak
sekuat ANOVA.

24. Statistik uji yang digunakan dalam analisis variansi adalah uji F, karena uji F digunakan untuk
membandingkan 2 variansi sampel.
3. A.
Uji Normalitas(berdasarkanjeniskelamin)
Tests of Normality
jenis_kelamin
Kolmogorov-Smirnova
Shapiro-Wilk
Statistic df Sig. Statistic df Sig.
data2 Laki-laki .100 20 .200*
.975 20 .859
Perempuan .117 20 .200*
.954 20 .432
a. Lilliefors Significance Correction
*. This is a lower bound of the true significance.
Uji Hipotesis
1. H0 : data berdistribusi normal
H1 : data tidakberdistribusi normal
2. Tingkatsignifikansi α =0.05
3. StatistikUji (Kolmogorov-Smirnov)
p-value Laki-laki =0.200
p-value Perempuan=0.200
4. Daerah kritik
Ho ditolakjikap-value <α
5. Kesimpulan
Karenasemuap_value > α makaHo tidakditolakuntukseluruhHo,maka databerdistribusi
normal
Uji Normalitas(berdasarkankelompokkerja)

25. Tests of Normality
kelomp
ok
Kolmogorov-Smirnova
Shapiro-Wilk
Statistic df Sig. Statistic df Sig.
data2 A .196 8 .200*
.881 8 .192
B .188 8 .200*
.931 8 .522
C .221 8 .200*
.914 8 .386
D .139 8 .200*
.965 8 .855
E .188 8 .200*
.888 8 .224
a. Lilliefors Significance Correction
*. This is a lower bound of the true significance.
Uji Hipotesis
1. H0 : data berdistribusi normal
H1 : data tidakberdistribusi normal
2. Tingkatsignifikansi α =0.05
3. StatistikUji (Kolmogorov-Smirnov)
p-value A = 0.200
p-value B= 0.200
p-value C= 0.200
p-value D= 0.200
p-value E= 0.200
4. Daerah kritik
Ho ditolakjikap-value <α
5. Kesimpulan
Karenasemuap_value > α makaHo tidakditolakuntukseluruhHo,maka databerdistribusi
normal
Uji Normalitas (berdasarkan shift kerja)

26. Tests of Normality
shift
Kolmogorov-Smirnova
Shapiro-Wilk
Statistic df Sig. Statistic df Sig.
data2 1.00 .154 10 .200*
.965 10 .839
2.00 .203 10 .200*
.862 10 .080
3.00 .174 10 .200*
.940 10 .555
4.00 .203 10 .200*
.952 10 .688
a. Lilliefors Significance Correction
*. This is a lower bound of the true significance.
Uji Hipotesis
1. H0 : data berdistribusi normal
H1 : data tidakberdistribusi normal
2. Tingkatsignifikansi α =0.05
3. StatistikUji (Kolmogorov-Smirnov)
p-value 1= 0.200
p-value 2= 0.200
p-value 3= 0.200
p-value 4= 0.200
4. Daerah kritik
Ho ditolakjikap-value <α
5. Kesimpulan
Karenasemuap_value > α makaHo tidakditolakuntukseluruhHo,maka databerdistribusi
normal
Uji Kesamaan Variansi

27. Test of Homogeneity of Variance
Levene Statistic df1 df2 Sig.
data2 Based on Mean .215 1 38 .645
Based on Median .164 1 38 .688
Based on Median and with
adjusted df
.164 1 37.999 .688
Based on trimmed mean .184 1 38 .670
Uji Hipotesis
1. Ho : σ²1 = σ²2 =.....=σ²n (data bervariansi sama)
H1 : tidaksemuaσi² sama ( data tidakbervariansi sama)
2. Tingkatsignifikansi α =0.05
3. StatistikUji
p-value mean =0.645
p-value median=0.688
4. Daerah kritik
Ho ditolakjikap-value <α
5. Kesimpulan
Karenap_value meandanmedianmasing-masing>α makaHo tidakditolak.,makadata
memilikivariansi yangsama.
Karenakeduaasumsi dalamAnavaterpenuhi,makaAnavadapatlangsungdilakukan.
B.
ANOVA
data2
Sum of Squares df Mean Square F Sig.
Between Groups 1430.350 4 357.588 2.716 .045
Within Groups 4608.625 35 131.675
Total 6038.975 39
Uji Hipotesis

28. 1. Ho : µ1 = µ2 =.....= µn
H1 : tidaksemuaµi sama
2. Tingkatsignifikansi α =0.05
3. StatistikUji
p-value =0.045
4. Daerah kritik
Ho ditolakjikap-value <α
5. Kesimpulan
Karenap_value (0.045) < α (0.05) makaHo ditolak.,sehinggatidaksemuaµi samaatau
dengankata lainproduktifitaspekerjaberbeda.
Untuk mengetahui produktifitaskelompokkerjamanayangberbeda,digunakankontras.
Contrast Coefficients
Contras
t
kelompok
A B C D E
1 1 1 -.5 -.5 -1
Contrast Tests
Contrast Value of Contrast Std. Error t df Sig. (2-tailed)
data2 Assume equal variances 1 -5.4375 7.58998 -.716 35 .478
Does notassume equal
variances
1 -5.4375 8.24144 -.660 22.047 .516
Uji Hipotesis
1. Ho : L = 0
H1 : L ≠ 0
2. Tingkatsignifikansi α =0.05
3. StatistikUji (asumsi kesamaanvariansi terpenuhi)
p-value =0.478
4. Daerah kritik
Ho ditolakjikap-value <α
5. Kesimpulan

29. Karenap_value kontras(0.478) > α (0.05) maka Ho tidak ditolak.,sehinggaproduktifitas
pekerjaantarayang berpendidikanSMK, D3, dan S1 tidakberbedasecarasignifikan.
C.
ANOVAc,d
Model Sum of Squares df Mean Square F Sig.
1 Regression 1430.350 4 357.588 .052 .995a
Residual 246566.650 36 6849.074
Total 247997.000b
40
a. Predictors:K4, K3, K2, K1
b. This total sum of squares is not corrected for the constantbecause the constantis zero for
regression through the origin.
c. DependentVariable:data3
d. Linear Regression through the Origin
Uji Hipotesis
1. Ho : τ1 = τ2 =.....= τa-1 = 0
H1 : tidaksemuaτ1 = 0 ; i=1,2,....,a-1
2. Tingkatsignifikansi α =0.05
3. StatistikUji
p-value =0.995
4. Daerah kritik
Ho ditolakjikap-value <α
5. Kesimpulan
Karenap-value (0.995) > α (0.05) maka Ho tidakditolak,sehinggafaktorB(kelompokkerja)
tidakberpengaruh secarasignifikan terhadapproduktifitaspekerja.
D.

30. Tests of Between-Subjects Effects
DependentVariable:data2
Source
Type III Sum of
Squares df Mean Square F Sig.
Intercept Hypothesis 241958.025 1 241958.025 676.640 .000
Error 1430.350 4 357.588a
shift Hypothesis 159.275 3 53.092 .191 .901
Error 3340.850 12 278.404b
kelompok Hypothesis 1430.350 4 357.588 1.284 .330
Error 3340.850 12 278.404b
shift* kelompok Hypothesis 3340.850 12 278.404 5.023 .001
Error 1108.500 20 55.425c
a. MS(kelompok)
b. MS(shift * kelompok)
c. MS(Error)
Uji Interaksi
Sigshift*kelompok=0.001 < α (0.05), makaHo ditolak,sehinggaadainteraksi/pengaruhantara
shiftdankelompokkerjadalamproduktifitaskerja.
E.

31. Tests of Between-Subjects Effects
DependentVariable:data2
Source
Type III Sum of
Squares df Mean Square F Sig.
Intercept Hypothesis 241958.025 1 241958.025 676.640 .000
Error 1430.350 4 357.588a
jenis_kelamin Hypothesis 24.025 1 24.025 .346 .588
Error 277.350 4 69.338b
shift Hypothesis 159.275 3 53.092 .191 .901
Error 3340.850 12 278.404c
kelompok Hypothesis 1430.350 4 357.588 1.219 .358
Error 3192.551 10.883 293.354d
jenis_kelamin * shift Hypothesis 154.475 3 51.492 .947 .449
Error 652.650 12 54.387e
jenis_kelamin * kelompok Hypothesis 277.350 4 69.338 1.275 .333
Error 652.650 12 54.387e
shift* kelompok Hypothesis 3340.850 12 278.404 5.119 .004
Error 652.650 12 54.387e
jenis_kelamin * shift*
kelompok
Hypothesis 652.650 12 54.387 . .
Error .000 0 .f
a. MS(kelompok)
b. MS(jenis_kelamin * kelompok)
c. MS(shift * kelompok)
d. MS(jenis_kelamin * kelompok) + MS(shift * kelompok) - MS(jenis_kelamin * shift* kelompok)
e. MS(jenis_kelamin * shift* kelompok)
f. MS(Error)
1. Uji Interaksi ketigafaktor

32. Sigjenis_kelamin*shift*kelompoktidakada,sehinggatidakdapatdiuji.
2. Uji efekjenis_kelamin*shift
Sigjenis_kelamin*shift=0.449 > α (0.05), maka Ho diterima,sehingga tidakada interaksi antara
faktorjenis_kelamindenganshift.
3. Uji jenis_kelamin*kelompok
Sigjenis_kelamin*kelompok =0.333 > α (0.05), makaHo diterima,sehingga tidakada interaksi
antara faktorpetugasdenganwaktu.
4. Uji efekshift*kelompok
Sigshift*kelompok=0.004 < α (0.05), makaHo ditolak,sehingga adainteraksi antarafaktorshift
dengankelompok.
5. Uji efekfaktorjenis_kelamin
Sigjenis_kelamin=0.588 > α (0.05), maka Ho diterima,sehinggafaktorjenis_kelamin tidak
berpengaruhsecara signifikan.
6. Uji efekfaktorshift
Sigshift= 0.901 > α (0.05),maka Ho diterima, sehinggafaktorshift tidakberpengaruhsecara
signifikan.
7. Uji efekfaktorkelompok
Sigkelompok=0.358 > α (0.05), maka Ho diterima,sehinggafaktorkelompok tidak
berpengaruhsecara signifikan.