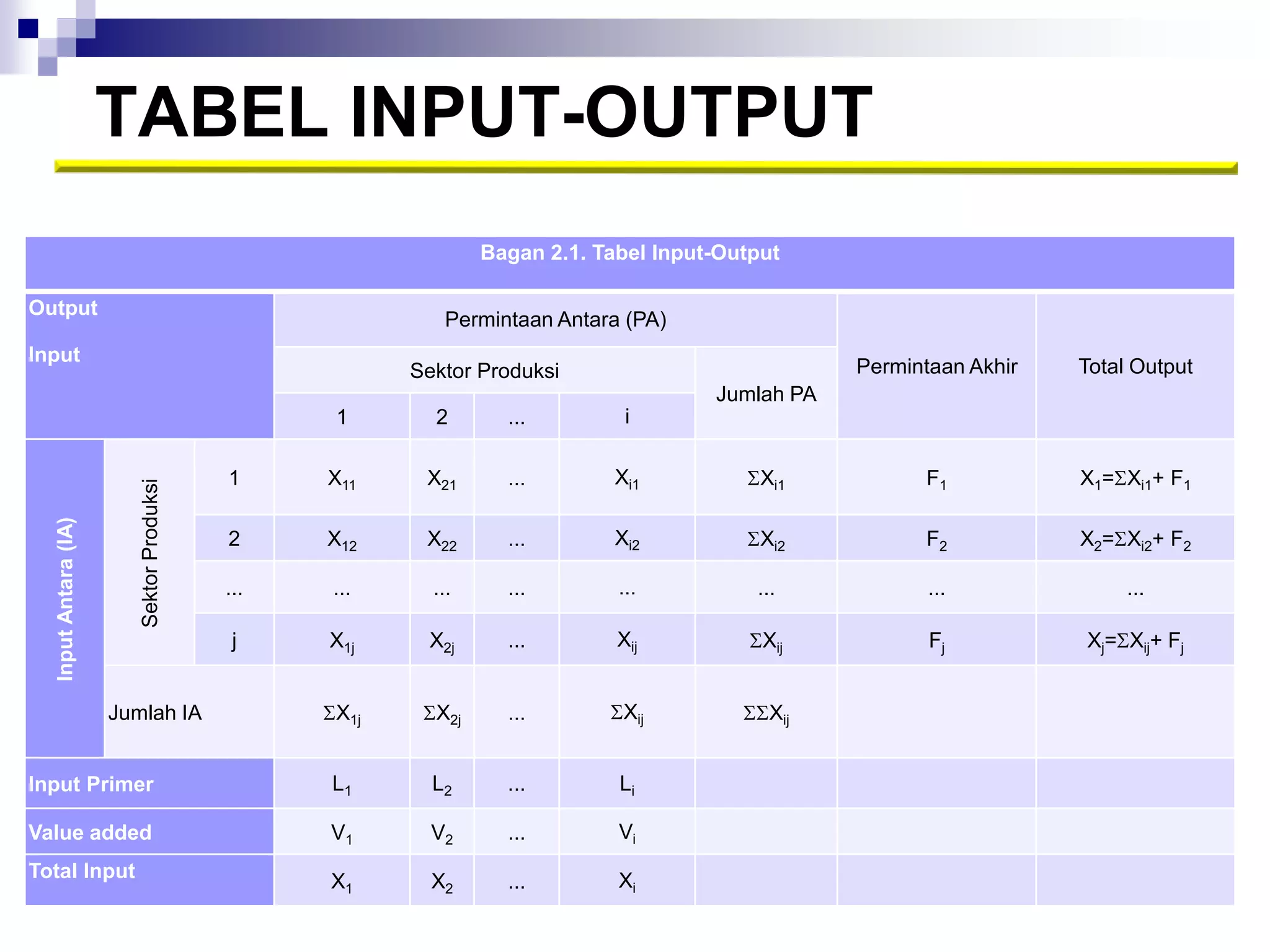
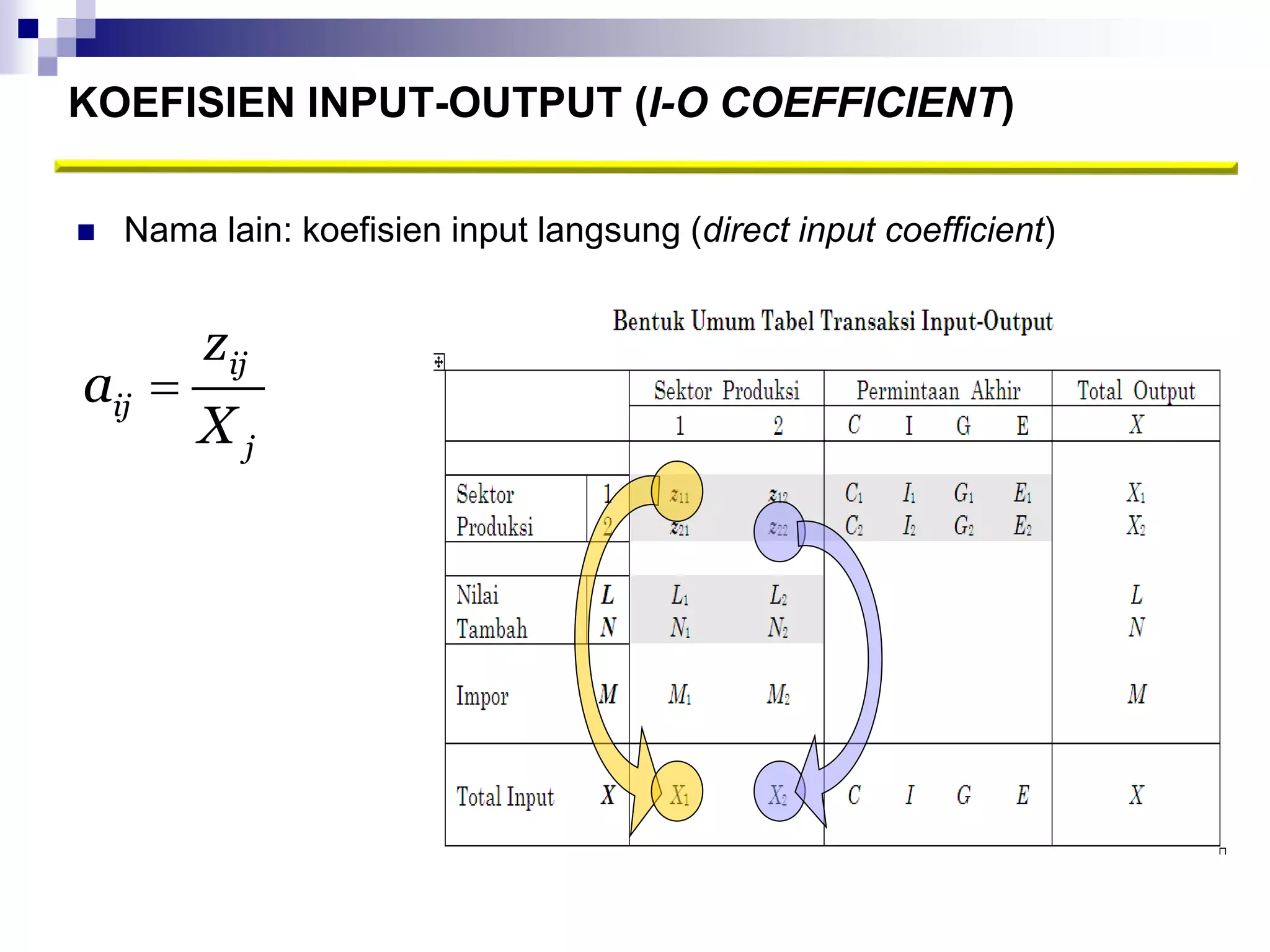
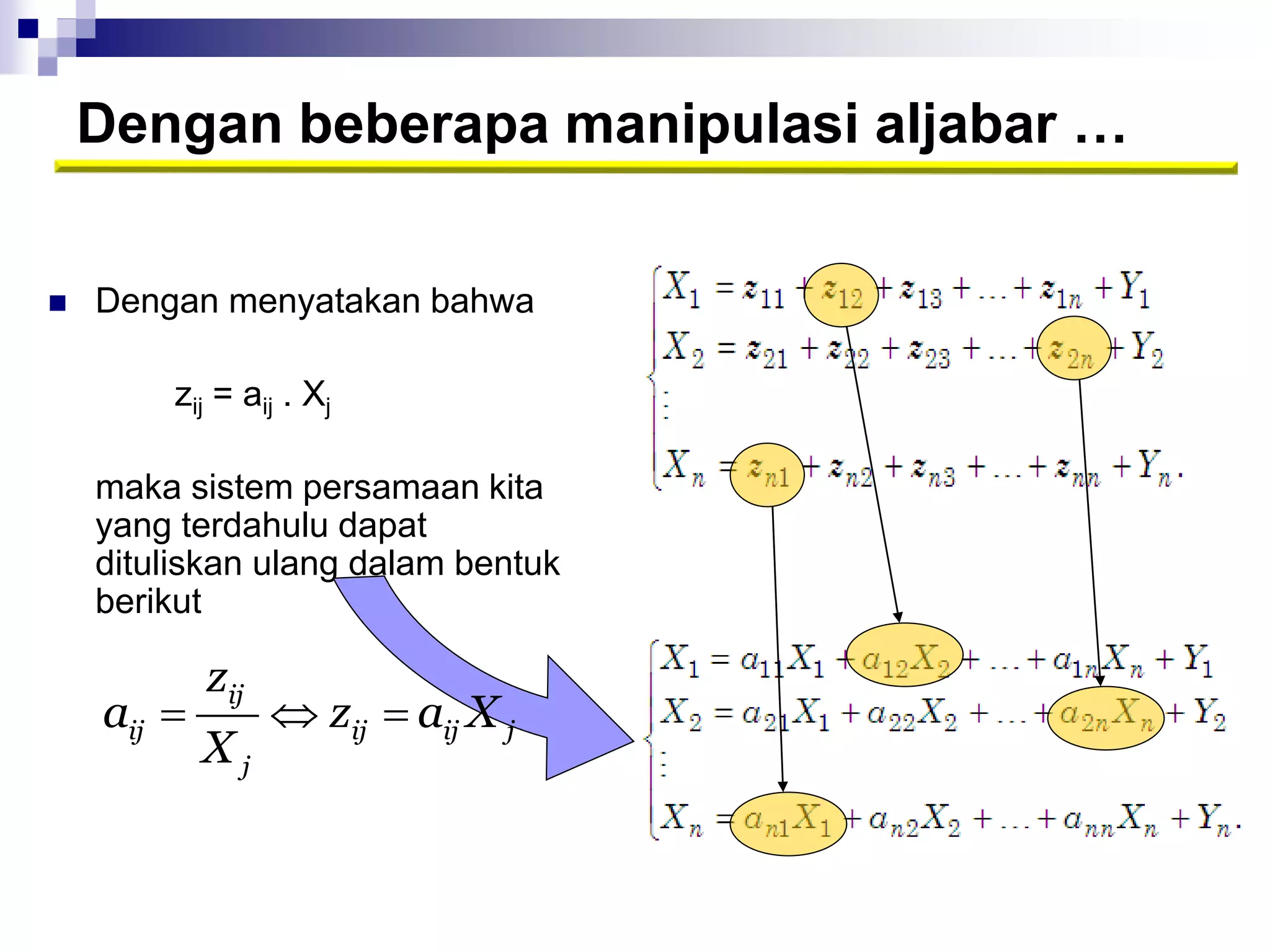
Dokumen ini membahas analisis input-output untuk memproyeksikan produksi, meramalkan kebutuhan tenaga kerja, dan mengidentifikasi sektor kunci. Tabel input-output digunakan untuk meramalkan dampak dari perubahan dan menghitung angka pengganda output, pendapatan rumah tangga, serta penyerapan tenaga kerja. Analisis ini penting untuk memahami hubungan antara permintaan akhir dan variabel endogen dalam perekonomian.

1. PEMAHAMAN ANALISIS
INPUT OUTPUT

2. Tujuan Analisis I-O
 memproyeksikan dan peramalan produksi atau
penyediaan kebutuhan sektoral untuk memenuhi
tuntutan sektoral tersirat oleh target alternatif untuk PDB
 meramalkan kebutuhan tenaga kerja terampil,
peningkatan kapasitas sektoral dan investasi
 Mengidentifikasi key sectors
 Tabel input-output juga dapat digunakan untuk
meramalkan dampak dari guncangan
 diterapkan untuk menentukan perbandingan-keuntungan

3. TABEL INPUT-OUTPUT
Bagan 2.1. Tabel Input-Output
Output
Input
Permintaan Antara (PA)
Permintaan Akhir Total OutputSektor Produksi
Jumlah PA
1 2 ... i
InputAntara(IA)
SektorProduksi
1 X11 X21 ... Xi1 Xi1 F1 X1=Xi1+ F1
2 X12 X22 ... Xi2 Xi2 F2 X2=Xi2+ F2
... ... ... ... ... ... ... ...
j X1j X2j ... Xij Xij Fj Xj=Xij+ Fj
Jumlah IA X1j X2j ... Xij Xij
Input Primer L1 L2 ... Li
Value added V1 V2 ... Vi
Total Input X1 X2 ... Xi

4. KOEFISIEN INPUT-OUTPUT (I-O COEFFICIENT)
 Nama lain: koefisien input langsung (direct input coefficient)
ij
ij
j
z
a
X


5. MATRIKS TEKNOLOGI
 Jika ada n sektor, maka akan
ada nxn banyaknya koefisien
input-output aij.
 Keseluruhan koefisien tersebut
dapat disajikan dalam sebuah
matriks A sebagai berikut
 Matriks ini disebut pula matriks
teknologi
 Salah satu konsekuensi dari
perhitungan koefisien input-
output ialah sebagai berikut:
ij
ij ij ij j
j
z
a z a X
X
  













nnnn
n
n
aaa
aaa
aaa




21
22221
11211
A

6. Dengan beberapa manipulasi aljabar …
 Dengan menyatakan bahwa
zij = aij . Xj
maka sistem persamaan kita
yang terdahulu dapat
dituliskan ulang dalam bentuk
berikut
ij
ij ij ij j
j
z
a z a X
X
  

7. Dan beberapa manipulasi aljabar lagi …
11 12 1 1 1
21 22 2 2 2
1 2
1
1
1
n
n
n n nn n n
a a a X Y
a a a X Y
a a a X Y
      
          
    
    
          
1 11 1 12 2 1 1
2 21 1 22 2 2 2
1 1 2 2
n n
n n
n n n nn n n
X a X a X a X Y
X a X a X a X Y
X a X a X a X Y
    

    


     
11 1 12 2 1 1
21 1 22 2 2 2
1 1 2 2
(1 )
(1 )
(1 ) .
n n
n n
n n nn n n
a X a X a X Y
a X a X a X Y
a X a X a X Y
    

     


     
(I- A)X= Y

8. SEHINGGA JIKA KITA BERTANYA:
 Bagaimanakah efek suatu perubahan eksogen (yaitu perubahan
pada nilai permintaan akhir Y) terhadap output X?
Kita ketahui bahwa (I – A)X = Y. Maka,
Matriks
Leontief Inverse
-1
X = (I - A) Y

9. LEONTIEF INVERSE DAN PENGGANDA KEYNES
11 12 1
21 22 2
1 2
n
n
n n nn
b b b
b b b
b b b
 
 
  
 
 
  
-1
(I - A) B
1
0 0 0(1 )
( )c
Y C I G
  
-1
X=(I- A) Y

10. TABEL TRANSAKSI PEREKONOMIAN HIPOTETIS
Sektor Produksi Permintaan Akhir Total Output
1 2 C I X
Sektor
Produksi
1 100 400 300 200 1000
2 300 600 500 600 2000
Input
Primer
L 200 700
N 400 300
Total Input 1000 2000
1
10001
1
2000
100 400 0ˆ( )
300 600 0
0,1 0,2
0,3 0,3
    
     
   
 
  
 
A Z X





















7,03,0
2,09,0
3,03,0
2,01,0
10
01
A)(I






 
579,1526,0
351,0228,1
)( 1
AI

11. PERUBAHAN FINAL DEMAND
.
947,578
877,350
300
200
579,1526,0
351,0228,1
)(



















 

 1t
1
1t YAIX

12. TIGA MACAM ANGKA PENGGANDA
 Pengganda output (output multiplier)
 Pengganda pendapatan rumah tangga (income multiplier)
 Pengganda tenaga kerja (employment multiplier)

13. ANGKA PENGGANDA
 Analisis angka pengganda mencoba melihat apa yang
terjadi terhadap variabel-variabel endogen, yaitu output
sektoral, apabila terjadi perubahan variabel-variabel
eksogen, seperti permintaan akhir, di perekonomian
Perubahan
variabel eksogen
--- konsumsi, investasi,
pengeluaran pemerintah ---
Perubahan
variabel endogen
--- output/produksi ---
Angka pengganda
(multiplier)

14. ANGKA PENGGANDA OUTPUT
 Jika ada tambahan final demand sebesar Rp 1 di satu
sektor tertentu (katakan sektor i), berapa besar
tambahan output sektor tersebut?
Rp 1 tambahan final demand
di sektor i
--- konsumsi, investasi,
pengeluaran pemerintah ---
Tambahan output
di sektor i
Angka pengganda output
(output multiplier)

15. CONTOH KASUS
0,1 0,2
0,3 0,3
 
  
 
A
1,228 0,351
0,526 1,579
  
   
 
1
(I A)
Katakan terdapat tambahan final demand sebesar Rp 1 untuk sektor 1
sementara final demand sektor 2 tidak berubah. Dituliskan,
1
0
 
   
 
Y 
   1
X (I A) YDengan menggunakan
1,228 0,351 1 1,228
0,526 1,579 0 0,526
    
      
    
X
1
1,754 unit uang
1,754
1 unit uang
O  
Angka pengganda (multiplier) output sektor 1:

16. Untuk sektor 2, dan seterusnya …
Dengan cara yang sama, jika terdapat tambahan final demand sebesar Rp 1
untuk sektor 2, sementara final demand sektor 1 tidak berubah, maka
0
1
 
   
 
Y 
   1
X (I A) Y
1,228 0,351 0 0,351
0,526 1,579 1 1,579
    
      
    
X
2
1,930 unit uang
1,930
1 unit uang
O  
Angka pengganda (multiplier) output sektor 2:
Dengan menggunakan
1
n
j ij
i
O b

 Sehingga secara umum dapat dituliskan

17. ANGKA PENGGANDA PENDAPATAN RT
 Jika ada tambahan final demand sebesar Rp 1 di satu sektor
tertentu (katakan sektor i), berapa besar tambahan pendapatan
rumah tangga di sektor tersebut?
 Pendapatan rumah tangga berasal dari penerimaan gaji/upah
tenaga kerja – yang pada gilirannya merupakan proporsi tertentu
dari output yang diproduksi
Rp 1 tambahan final demand
di sektor i
--- konsumsi, investasi,
pengeluaran pemerintah ---
Tambahan output
di sektor i
Angka pengganda output
(output multiplier)
Tambahan
pendapatan
rumah tangga
di sektor i
Angka pengganda
pendapatan rumah tangga
(household income
multiplier)

18. HUBUNGAN OUTPUT- PENDAPATAN RUMAH TANGGA
 Pendapatan rumah
tangga berasal dari
pembayaran upah/gaji
oleh sektor produksi
 Untuk setiap Rp1
output sektor i,
berapakah proporsi
yang dikeluarkan untuk
membayar upah/gaji?
 Dapat dilihat pada mat-
riks input primer. Biasa-
nya diletakkan sebagai
input primer pertama Sehingga, proporsi upah/gaji dalam struktur produksi
Sektor i dapat dilihat pada koefisien an+1,i

19. CONTOH KASUS:
1,228 0,351
0,526 1,579
  
   
 
1
(I A)
1,1
1,2
0,2
0,35
n
n
a
a




Tambahan pendapatan rumah tangga:
1 (0,2)(1,228) +(0,35)(0,526)=0,4297H 
2 (0,2)(0,351) (0,35)(1,579) 0,6228H   
Ini adalah SIMPLE HOUSEHOLD
INCOME MULTIPLIER, dinotasikan:
1,
1
n
j n i ij
i
H a b

 

20. ANGKA PENGGANDA TENAGA KERJA
 Jika ada tambahan final demand sebesar Rp 1 di satu sektor
tertentu (katakan sektor i), berapa besar tambahan penyerapan
tenaga kerja di sektor tersebut?
 Terdapat hubungan yang proporsional antara output yang
diproduksi dengan jumlah tenaga kerja yang digunakan. Jika kita
ketahui besar tambahan output yang akan diproduksi, maka dapat
dihitung pula jumlah tenaga kerja yang diperlukan
Rp 1 tambahan final demand
di sektor i
--- konsumsi, investasi,
pengeluaran pemerintah ---
Tambahan output
di sektor i
Angka pengganda output
(output multiplier)
Tambahan
serapan
tenaga kerja
di sektor i
Angka pengganda
tenaga kerja
(employment multiplier)

21. CONTOH KASUS: MULTIPLIER TENAGA KERJA
1,228 0,351
0,526 1,579
  
   
 
1
(I A)
Tambahan jumlah pekerja:
Ini adalah SIMPLE EMPLOYMENT
MULTIPLIER, dinotasikan:
Kita membutuhkan data jumlah pekerja
Di setiap sektor. Katakan data yang ada:
Sektor 1 = 4 orang pekerja
Sektor 2 = 10 orang pekerja
Selanjutnya dapat dihitung rata-rata
pekerja untuk tiap satuan output:
Berarti: 1
4
0,004
1000
w  
2
10
0,005
2000
w  
1
2
(1,228)(0,004) (0,526)(0,005) 0,0075
(0,351)(0,004) (1,579)(0,005) 0,0093
E
E
  
  
1,
1
n
j n i ij
i
E w b

 
wj = Lj / Xj

22. Indeks Daya Penyebaran dan Indeks
Derajat Kepekaan
 Indeks daya penyebaran (Backwards Linkage)
 Indeks derajt kepekaan (Forward Linkage)

23. HASIL DAMPAK
INVESTASI

24. Hitunglah berapa dampak kenaikan
investasi di sektor tanaman pangan
terhadap output??