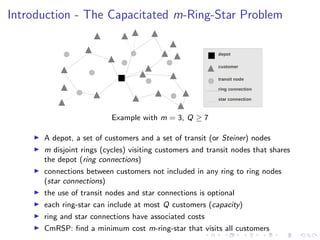
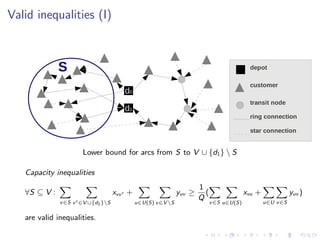
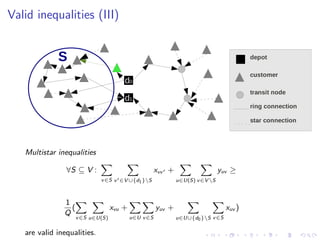
This document presents an integer linear programming formulation and branch-and-cut algorithm for the Capacitated m-Ring-Star Problem (CmRSP). The CmRSP involves finding minimum cost rings and connections to visit customers while respecting capacity constraints. The formulation is solved using a branch-and-cut algorithm with valid inequalities and heuristic separation routines. Computational results on benchmark instances show the algorithm outperforms CPLEX by solving larger instances to proven optimality faster and with smaller optimality gaps. Future work involves improving heuristics, branching strategies, and developing new valid inequalities and relaxations.

1. An Integer Linear Programming Formulation and
Branch-and-Cut Algorithm for the Capacitated
m-Ring-Star Problem (CmRSP)
Hern´an Berinsky
Paula Zabala
Departamento de Computaci´on
Facultad de Ciencias Exactas y Naturales
Universidad de Buenos Aires
hberins@dc.uba.ar
pzabala@dc.uba.ar

2. Introduction - The Capacitated m-Ring-Star Problem
R. Baldacci, M. Dell’Amico, J. Salazar Gonz´alez. The Capacitated
m-Ring-Star Problem, Operations Research Vol. 55, No. 6,
November-December 2007, pp. 1147-1162, INFORMS.
A. Mauttone, S. Nesmachnow, A. Olivera, F. Robledo. A hybrid
metaheuristic algorithm to solve the Capacitated m-Ring Star Problem,
2007, International Network Optimization Conference.
E. Hoshino, C. de Souza. Column Generation Algorithms for the
Capacitated m-Ring-Star Problem, Lecture Notes in Computer Science,
Springer Berlin / Heidelberg, Volume 5092/2008, June 2008.

3. Introduction - The Capacitated m-Ring-Star Problem
depot
customer
transit node
ring connection
star connection
Example with m = 3, Q ≥ 7
A depot, a set of customers and a set of transit (or Steiner) nodes
m disjoint rings (cycles) visiting customers and transit nodes that shares
the depot (ring connections)
connections between customers not included in any ring to ring nodes
(star connections)
the use of transit nodes and star connections is optional
each ring-star can include at most Q customers (capacity)
ring and star connections have associated costs
CmRSP: find a minimum cost m-ring-star that visits all customers

4. Integer Programming Formulation (I)
Depot is represented by d0 and d1 (copy of d0)
U = {u1, ..., u|U|} customers
W = {w1, ..., w|W |} transit (Steiner) nodes
V = U ∪ W
for v ∈ V ∪ {d0}, v ∈ V ∪ {d1}, cvv are the ring connection costs
for u ∈ U, v ∈ V , duv are the star connection costs
for v ∈ V ∪ {d0}, v ∈ V ∪ {d1}, v = v
xvv =
1 if there is a ring connection from v to v
0 other case
for u ∈ U, v ∈ V , u = v
yuv =
1 if there is a star connection from u to v
0 other case
for v ∈ V , fv ∈ Z is the number of customers visited (in a ring-star) in a
directed path from d0 to v in (including star connections)

5. Integer Programming Formulation (II)
min v∈V ∪{d0} v ∈V ∪{d1},v =v cvv xvv + u∈U v∈V ,v=u duv yuv
subject to
1. v∈V xd0v = m
2. v∈V xvd1 = m
3. v∈V ∪{d0},v=u xvu + v∈V ,v=u yuv = 1 ∀u ∈ U
4. v∈V ∪{d0},v=w xvw ≤ 1 ∀w ∈ W
5. v ∈V ∪{d0},v =v xv v = v ∈V ∪{d1},v =v xvv ∀v ∈ V
6. yuv ≤ v ∈V ∪{d0},v =v xv v ∀u ∈ U ∀v ∈ V u = v
7. fu ≥ 1 + u ∈U,u =u yu u ∀u ∈ U
8. fw ≥ u∈U yuw ∀w ∈ W
9. fu ≥ (fv + 1 + u ∈U,u =u yu u) − |U|(1 − xvu) ∀u ∈ U ∀v ∈ V u = v
10. fw ≥ (fv + u∈U yuw ) − |U|(1 − xvw ) ∀w ∈ W ∀v ∈ V w = v
11. 1 ≤ fv ≤ Q ∀v ∈ V

6. Valid inequalities (I)
d1
depot
customer
transit node
ring connection
star connection
S
d0
Lower bound for arcs from S to V ∪ {d1} S
Capacity inequalities
∀S ⊆ V :
v∈S v ∈V ∪{d1}S
xvv +
u∈U(S) v∈V S
yuv ≥
1
Q
(
v∈S u∈U(S)
xvu +
u∈U v∈S
yuv )
are valid inequalities.

7. Valid inequalities (II)
d1
depot
customer
transit node
ring connection
star connection
S
d0
Lower bound for arcs from S to V ∪ {d1} S, useful when |U(S)| < Q
Connectivity inequalities
∀S ⊆ V , ∀u ∈ U(S), |U(S)| ≥ 1:
v∈S v ∈V ∪{d1}S
xvv ≥
v∈V ∪{d0}
xvu +
v∈S
yuv
are valid inequalities.

8. Valid inequalities (III)
d1
depot
customer
transit node
ring connection
star connection
S
d0
Multistar inequalities
∀S ⊆ V :
v∈S v ∈V ∪{d1}S
xvv +
u∈U(S) v∈V S
yuv ≥
1
Q
(
v∈S u∈U(S)
xvu +
u∈U v∈S
yuv +
u∈U∪{d0}S v∈S
xuv )
are valid inequalities.

9. Valid inequalities (IV)
d1
depot
customer
transit node
ring connection
star connection
S
d0
Capacity bounded by constant
∀S ⊆ V , K =
|U(S)|
Q
:
v∈S v ∈V ∪{d1}S
xvv +
u∈U(S) v∈V S
yuv ≥ K
are valid inequalities.

10. Valid inequalities (V)
d1
depot
customer
transit node
ring connection
star connection
S
d0
If u is not connected to any node v ∈ V ∪ {d1} {u } then u is not
connected to u
If u is connected to u then u is connected to a node v ∈ V ∪ {d1}, v = u
Sum of customers
∀u, u ∈ U u = u : xu u + yu u ≤ xud1 +
v ∈V ,v =u,v =u
xuv + yuv
are valid inequalities.

11. Branch-and-Cut algorithm
Initial heuristic: we consider a two-phase method. In the first phase, an
heuristic chooses m customers. In the second phase, a greedy algorithm
builds the m rings introducing new customers iteratively considering some
ring and star connections posibilities in each iteration.
Branching strategies: best-bound for node selection and reduced
pseudo-costs for variable selection.
Separation routines: direct enumeration for separation problem in Sum
of customers inequalities, and heuristic algorithm for Capacity,
Connectivity, Multistar and Capacity bounded by constant inequalities.

12. Computational Results
(26,12,13,4,4)
(26,12,13,4,5)
(26,12,13,5,3)
(26,18,7,3,7)
(26,18,7,4,5)
(26,18,7,5,4)
(26,25,0,3,10)
(26,25,0,4,7)
(26,25,0,5,6)
(51,12,38,3,5)
(51,12,38,4,4)
(51,12,38,5,3)
(51,25,25,3,10)
(51,25,25,4,7)
(51,25,25,5,6)
0
200
400
600
800
1000
1200
1400
1600
1800
2000
Running time
CPLEX vs BC
Time_CPX Time_BC
Instance
Time[seconds]
(26,12,13,4,4)
(26,12,13,4,5)
(26,12,13,5,3)
(26,18,7,3,7)
(26,18,7,4,5)
(26,18,7,5,4)
(26,25,0,3,10)
(26,25,0,4,7)
(26,25,0,5,6)
(51,12,38,3,5)
(51,12,38,4,4)
(51,12,38,5,3)
(51,25,25,3,10)
(51,25,25,4,7)
(51,25,25,5,6)
0
5
10
15
20
25
%Gap
CPLEX vs BC
gap_CPX gap_BC
Instance
%Gap

13. Computational Results
(26,12,13,4,4)
(26,12,13,4,5)
(26,12,13,5,3)
(26,18,7,3,7)
(26,18,7,4,5)
(26,18,7,5,4)
(26,25,0,3,10)
(26,25,0,4,7)
(26,25,0,5,6)
(51,12,38,3,5)
(51,12,38,4,4)
(51,12,38,5,3)
(51,25,25,3,10)
(51,25,25,4,7)
(51,25,25,5,6)
0
200
400
600
800
1000
1200
1400
1600
1800
2000
Running time
CPLEX vs BC
Time_CPX Time_BC
Instance
Time[seconds]
(26,12,13,4,4)
(26,12,13,4,5)
(26,12,13,5,3)
(26,18,7,3,7)
(26,18,7,4,5)
(26,18,7,5,4)
(26,25,0,3,10)
(26,25,0,4,7)
(26,25,0,5,6)
(51,12,38,3,5)
(51,12,38,4,4)
(51,12,38,5,3)
(51,25,25,3,10)
(51,25,25,4,7)
(51,25,25,5,6)
0
20000
40000
60000
80000
100000
120000
# nodes explored
CPLEX vs BC
nod_CPX nod_BC
Instance
#nodesexplored

14. Conclusions and future work
Conclusions
Integer programming formulation
Initial heuristic (initial gap about ∼ 35%)
Branch-and-bound parameters: BB/RPC
Other features: Branch-and-cut IPC and skip factor, partially symmetry
breaking
Future work
Heuristics and metaheuristics: improve initial heuristic, implement a
primal heuristic
Analyze formulation specific variable/node branching selection
Valid inequalities and separation algorithms
Other kind of relaxations