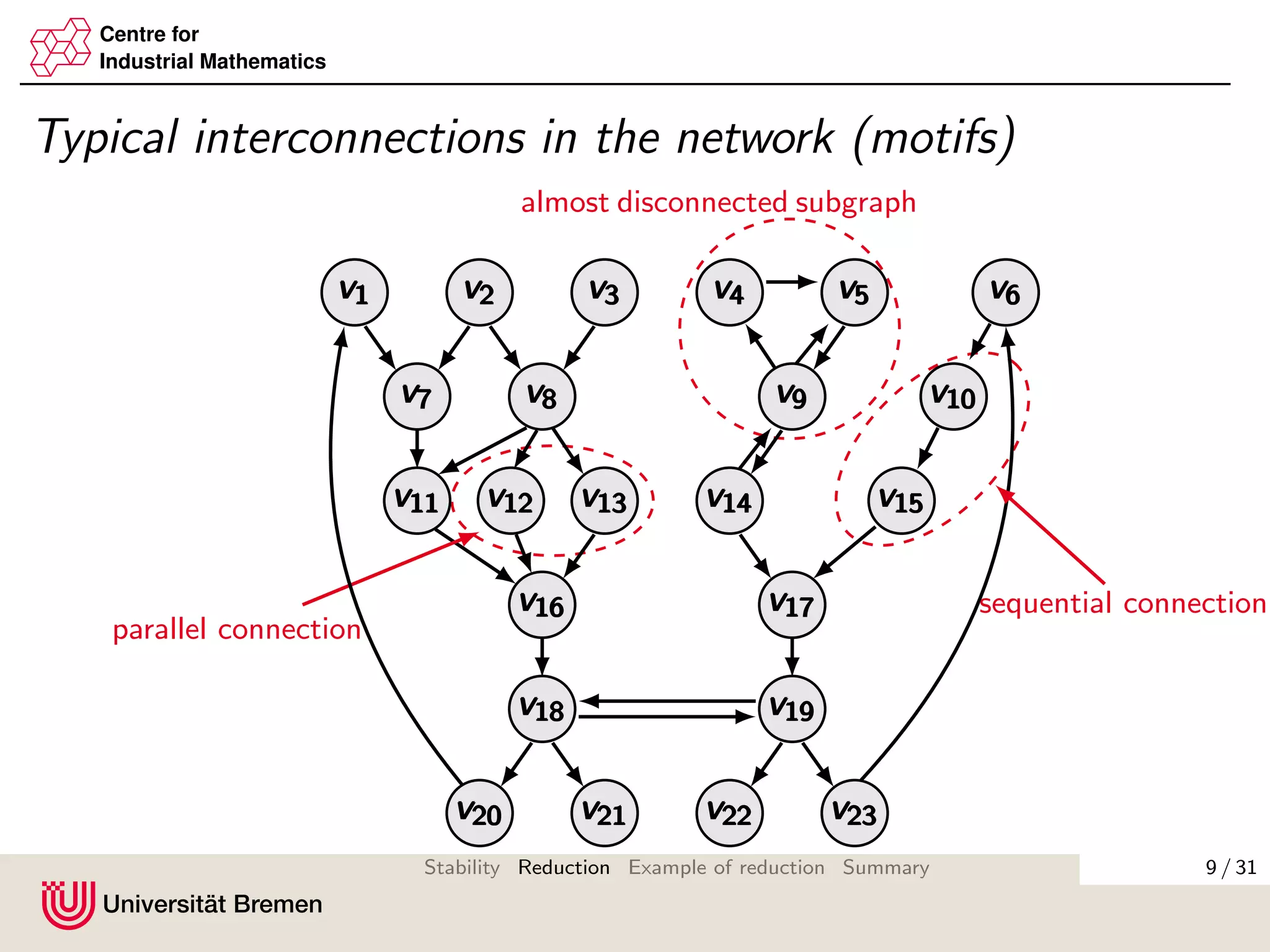
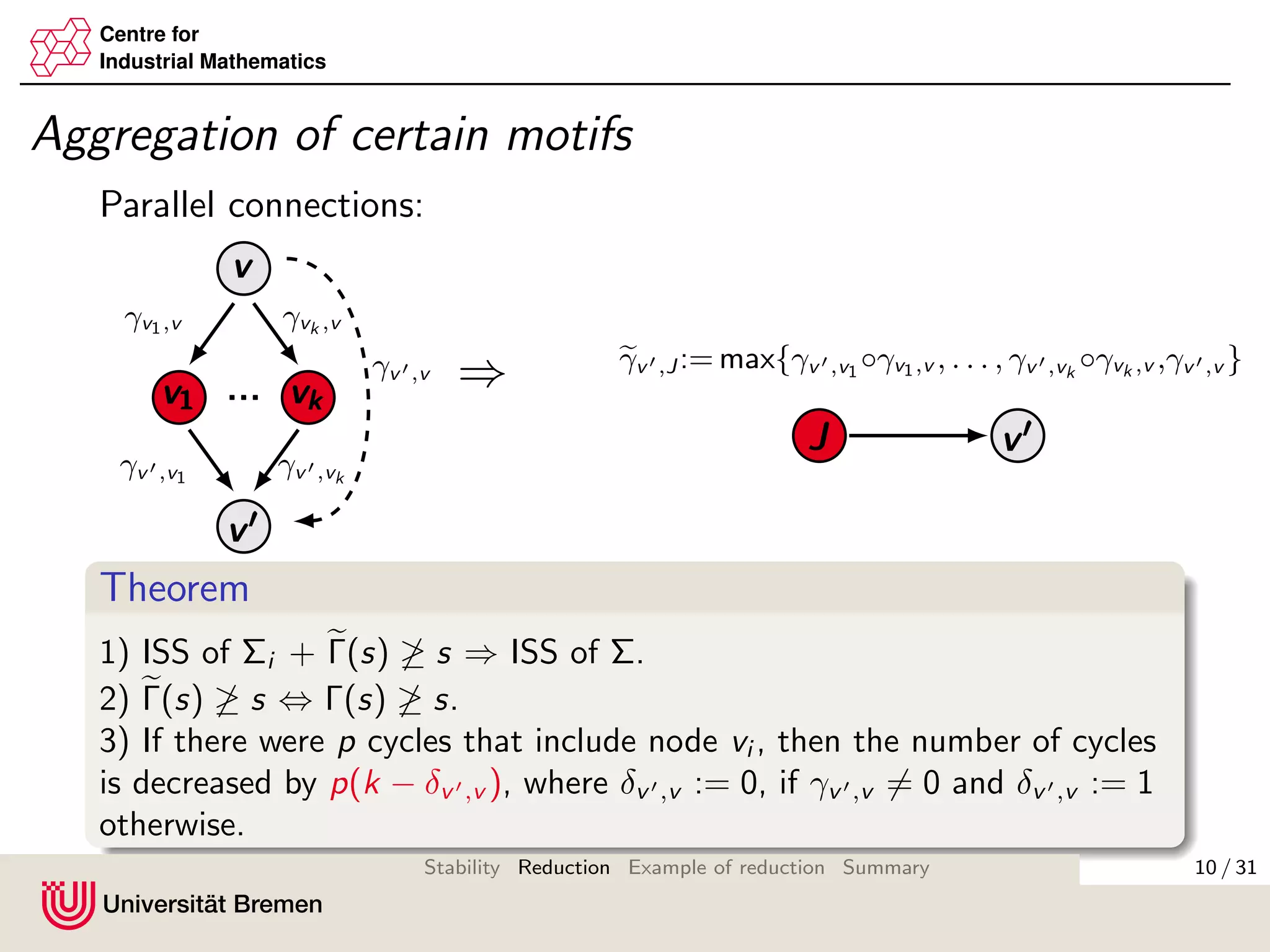
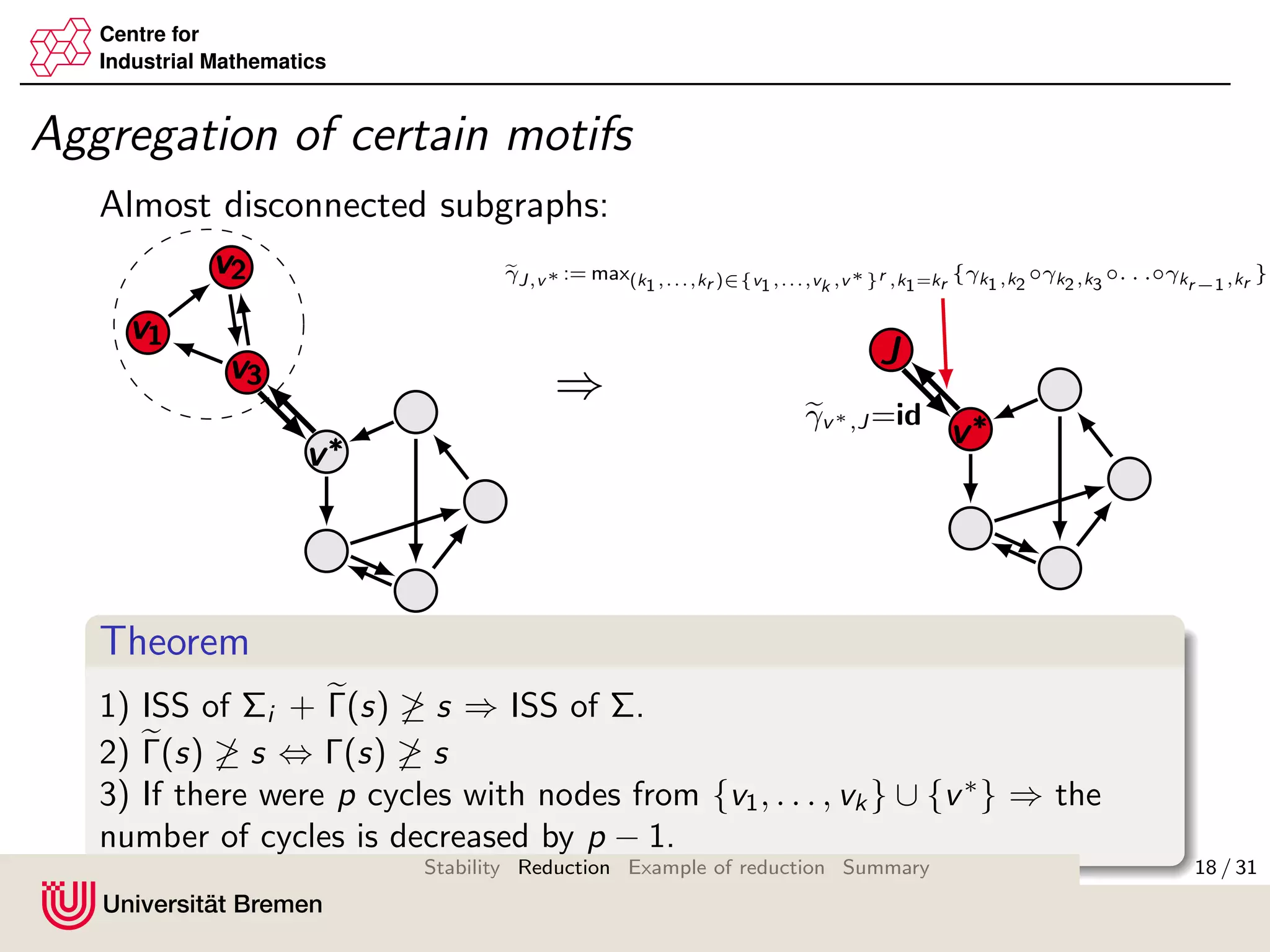
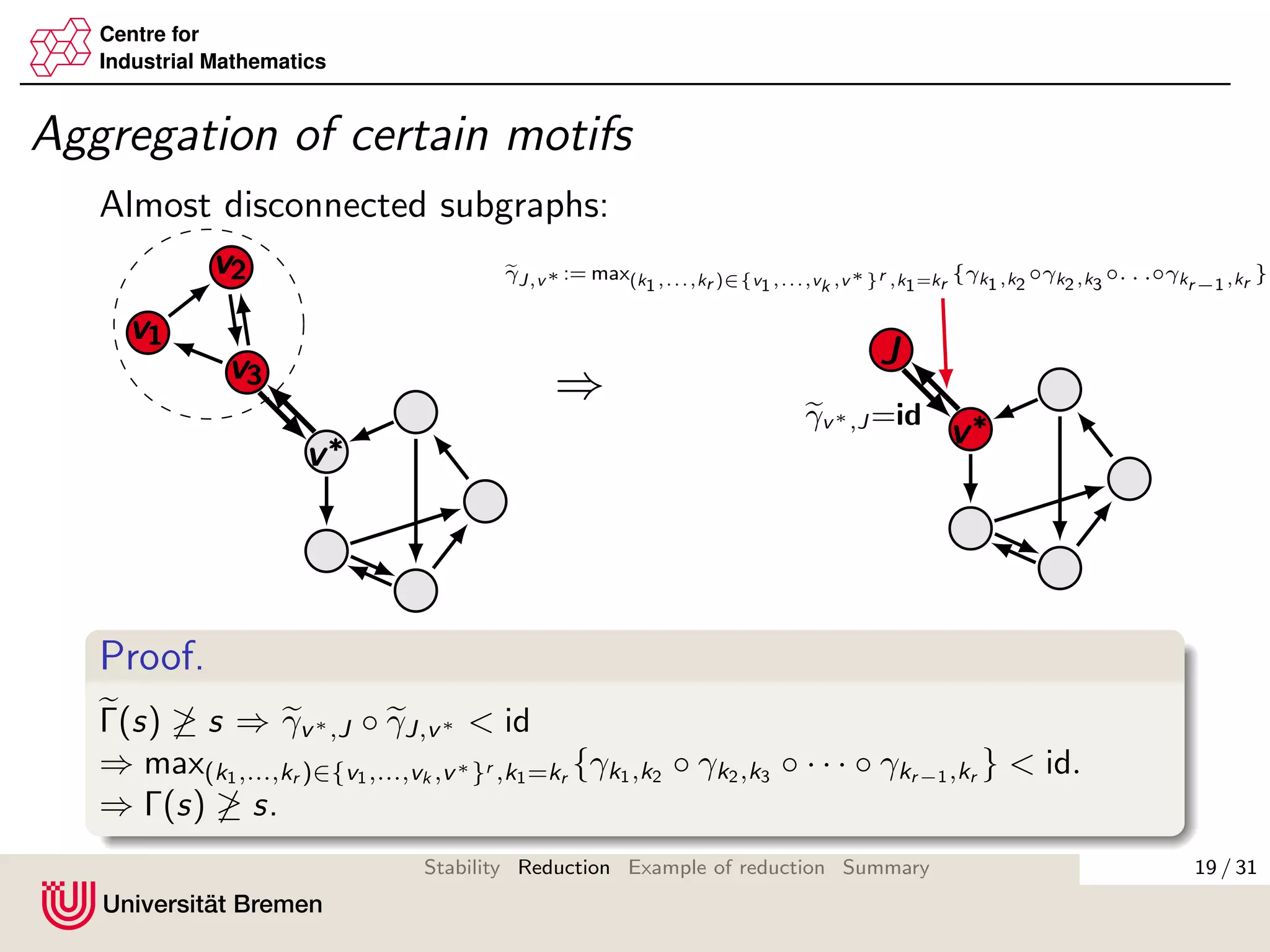
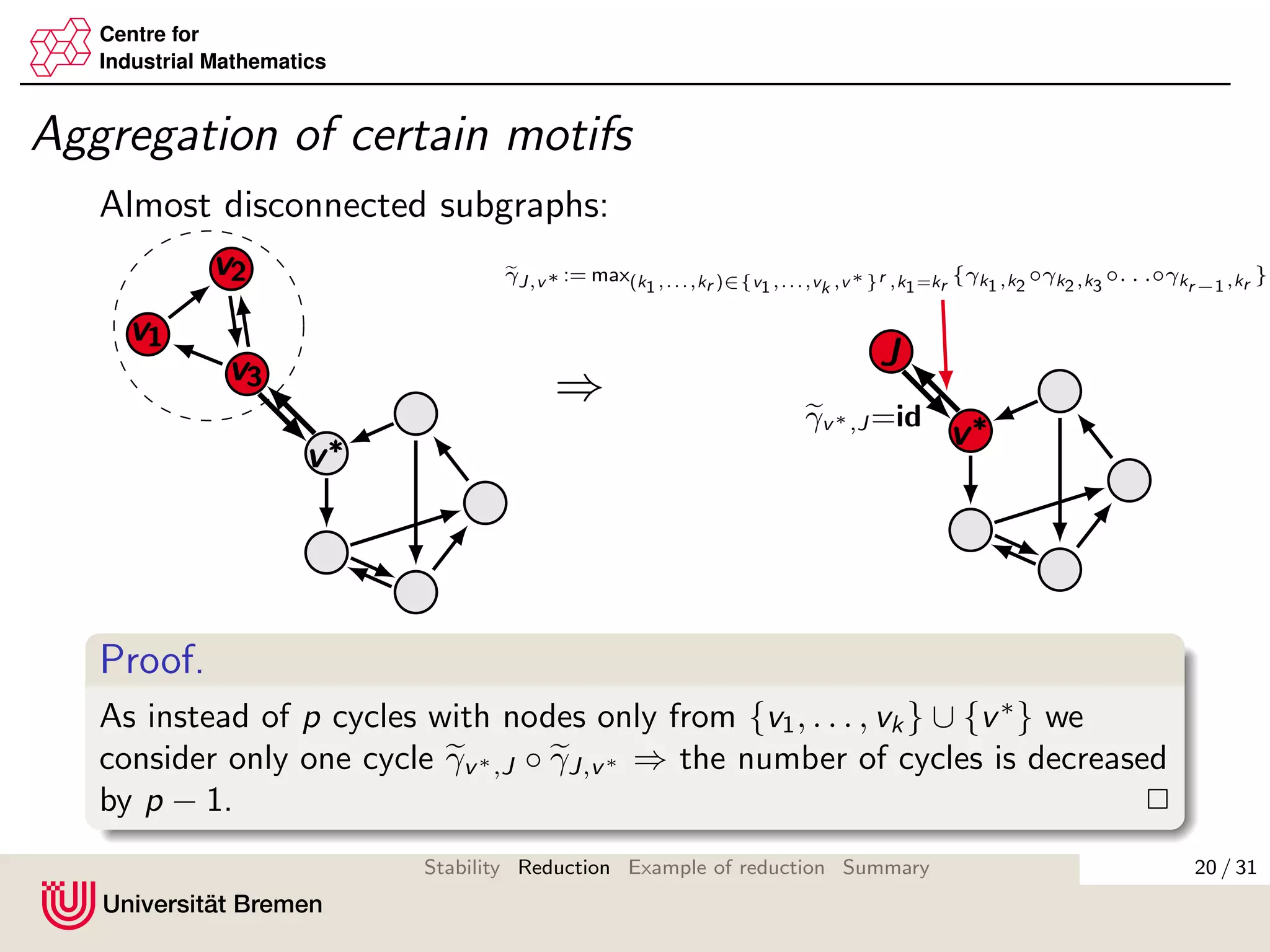
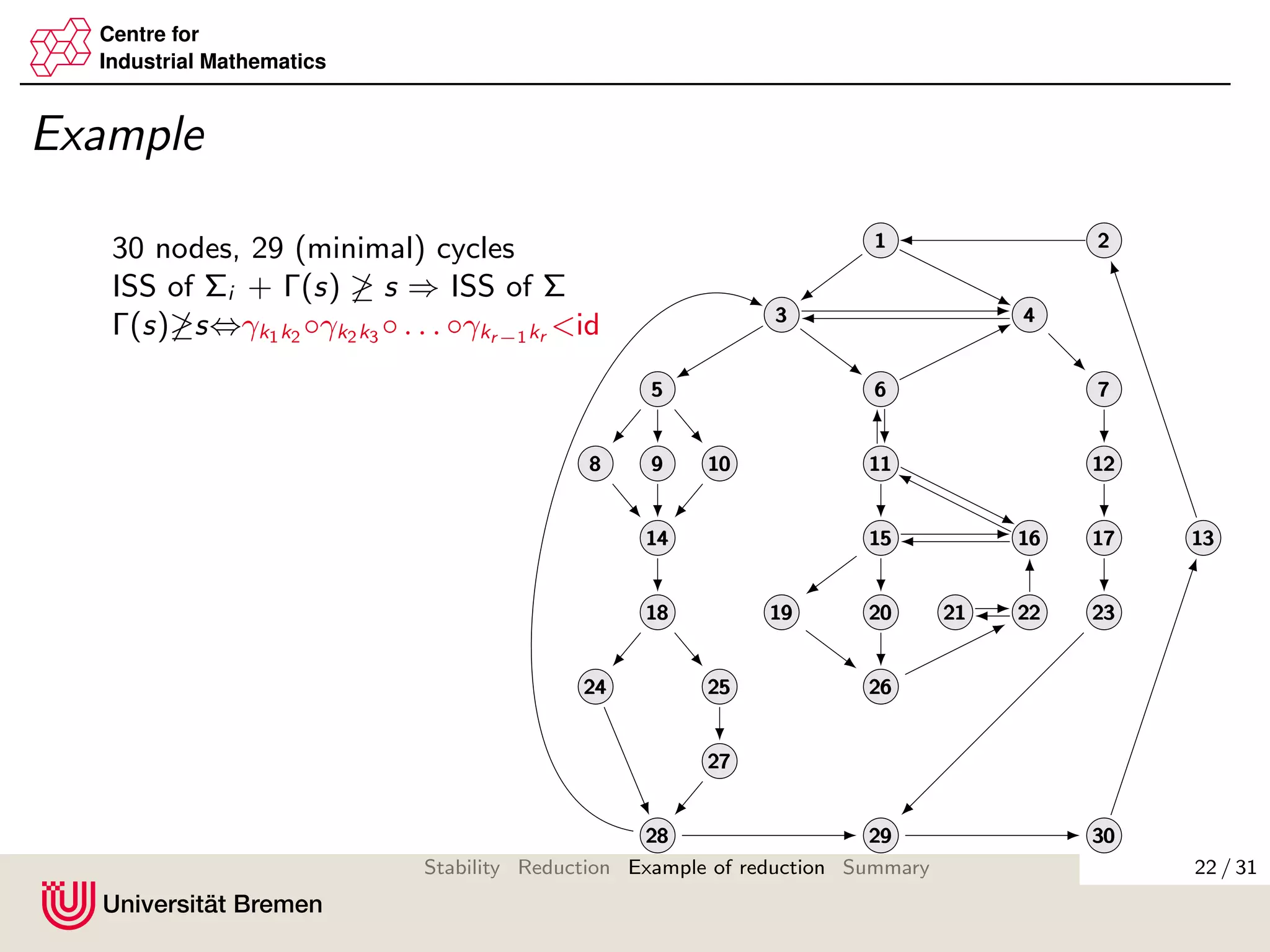
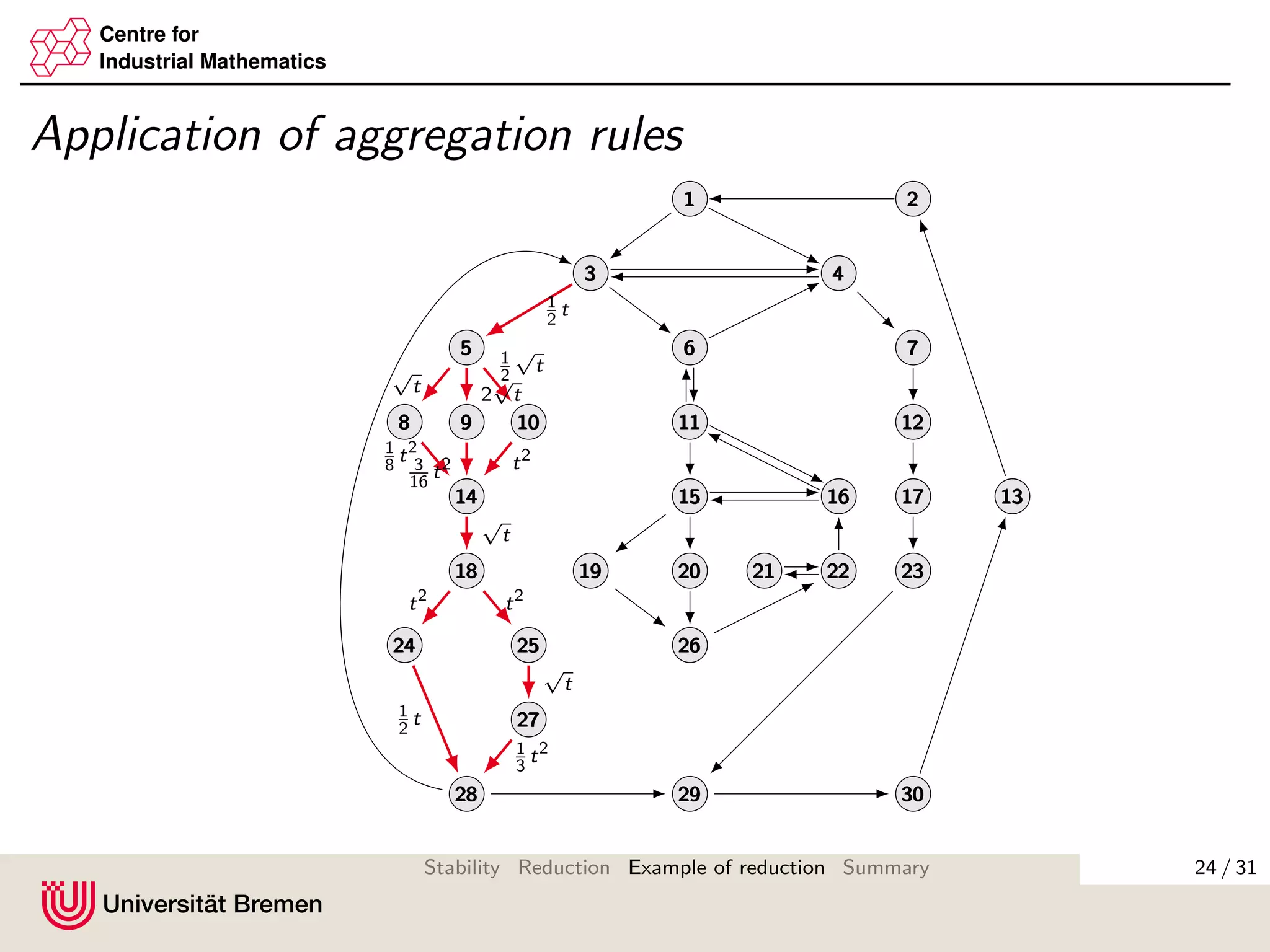
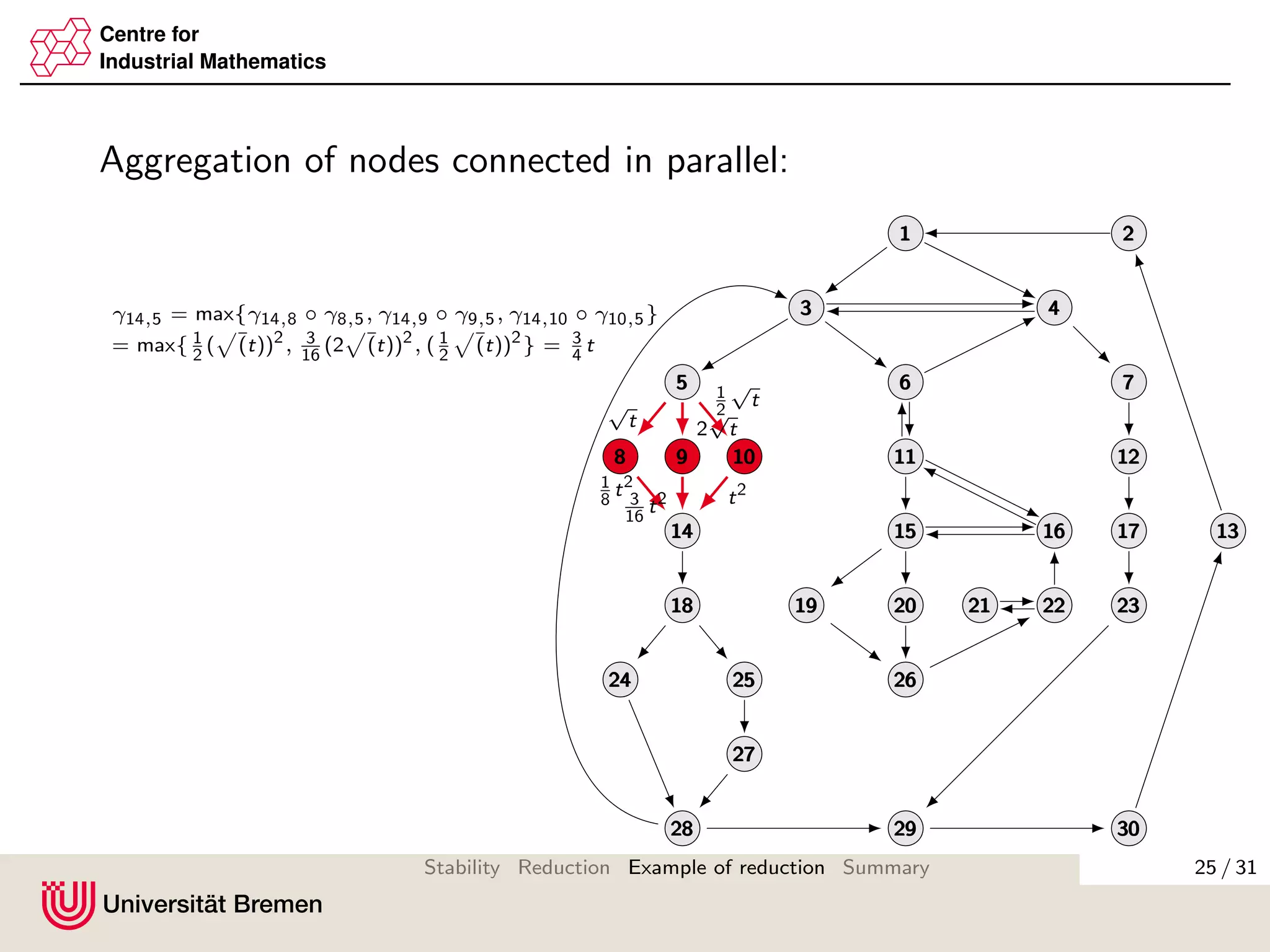
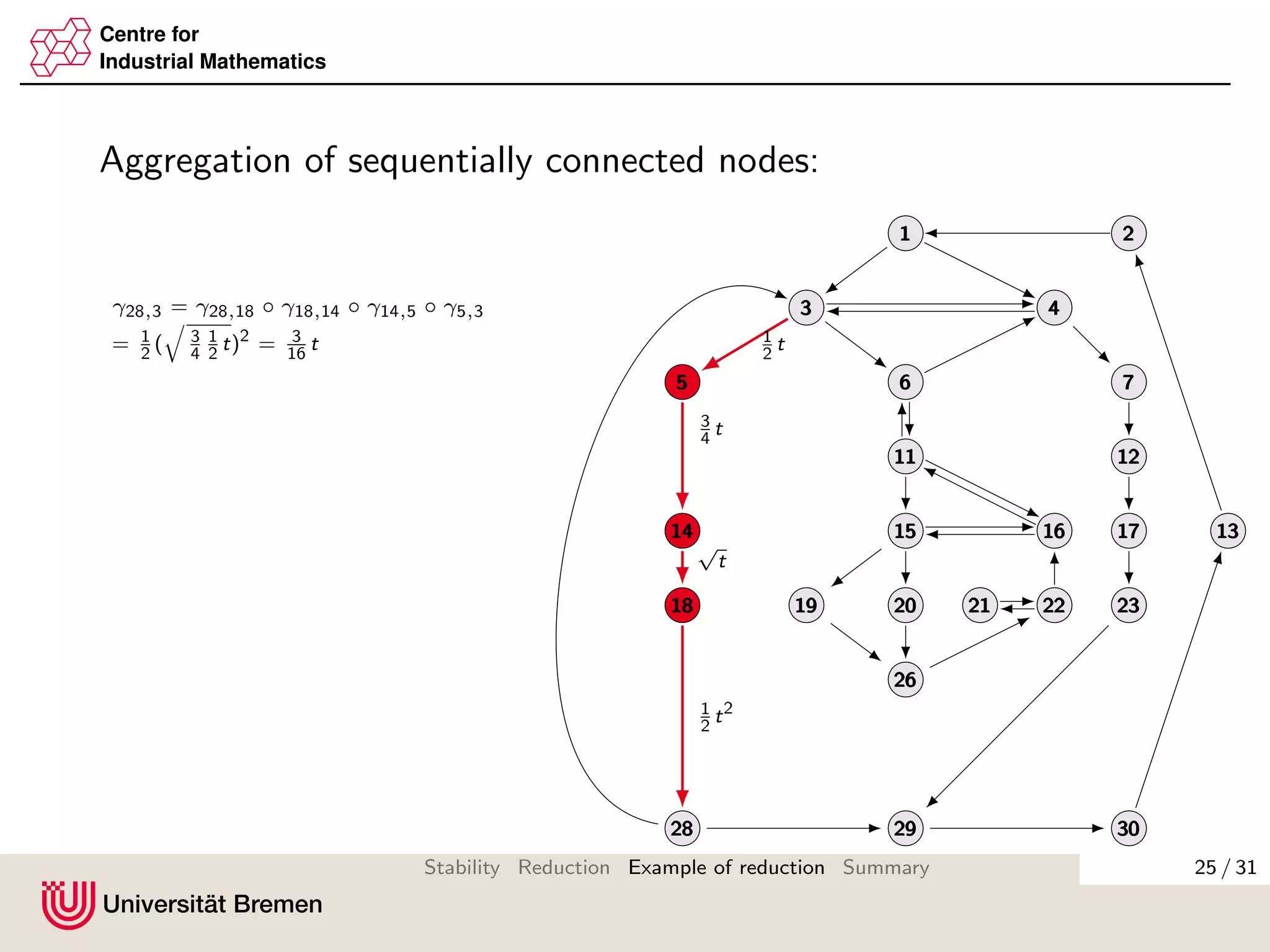
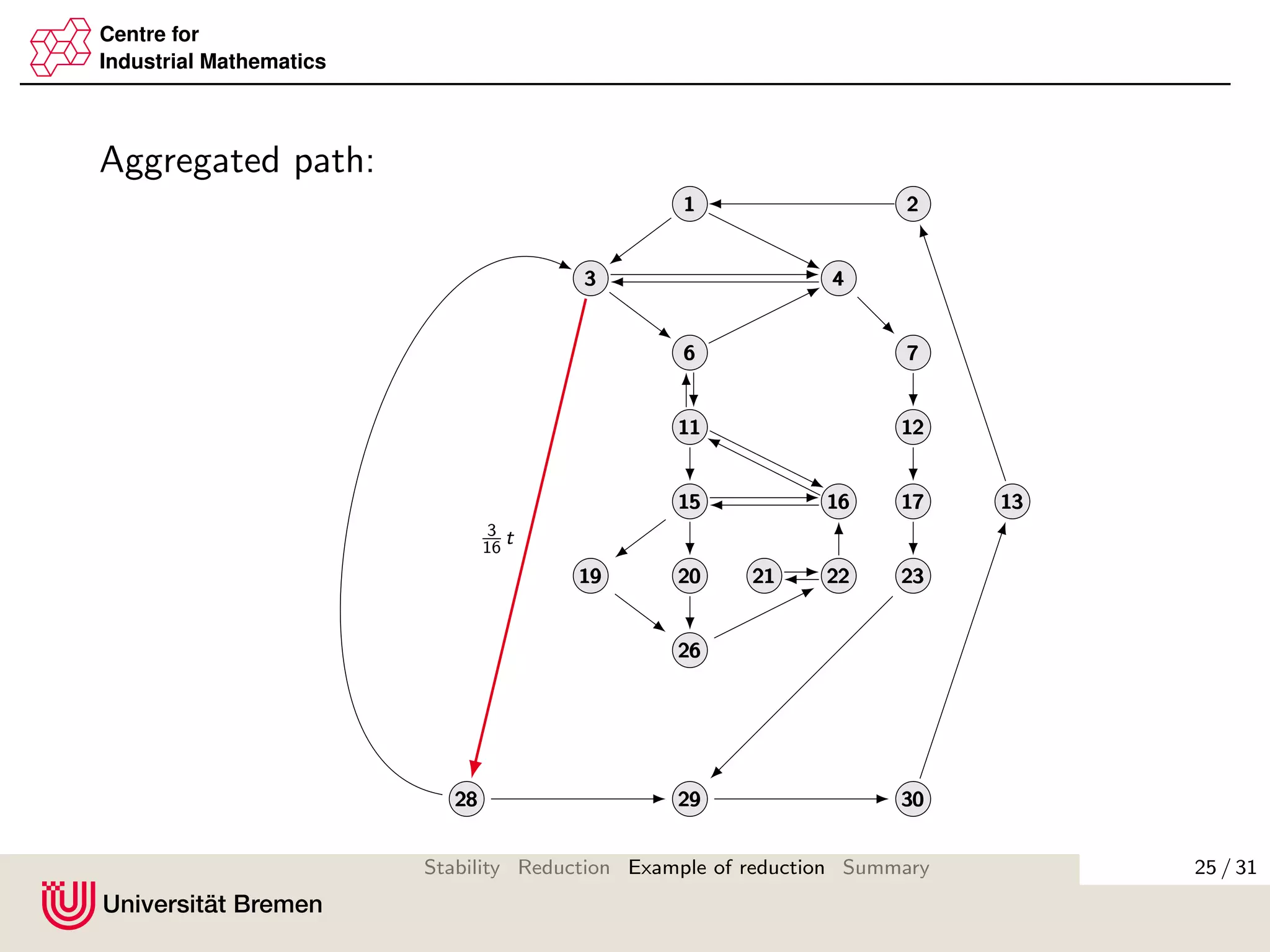
The document discusses methods for reducing the size of gain matrices used in analyzing the stability of interconnected systems. It proposes aggregating nodes in typical interconnection motifs like parallel and sequential connections to obtain a reduced gain matrix. This is done while preserving the small gain condition needed for input-to-state stability. Aggregating motifs involving almost disconnected subgraphs is also discussed. The reduction technique aims to simplify verifying the small gain condition for large networks.