Downloaded 47 times
Uploaded byÁkos Horváth
CPS(M): Constraint Satisfaction Problem over Models (a.k.a rule based design space exploration)
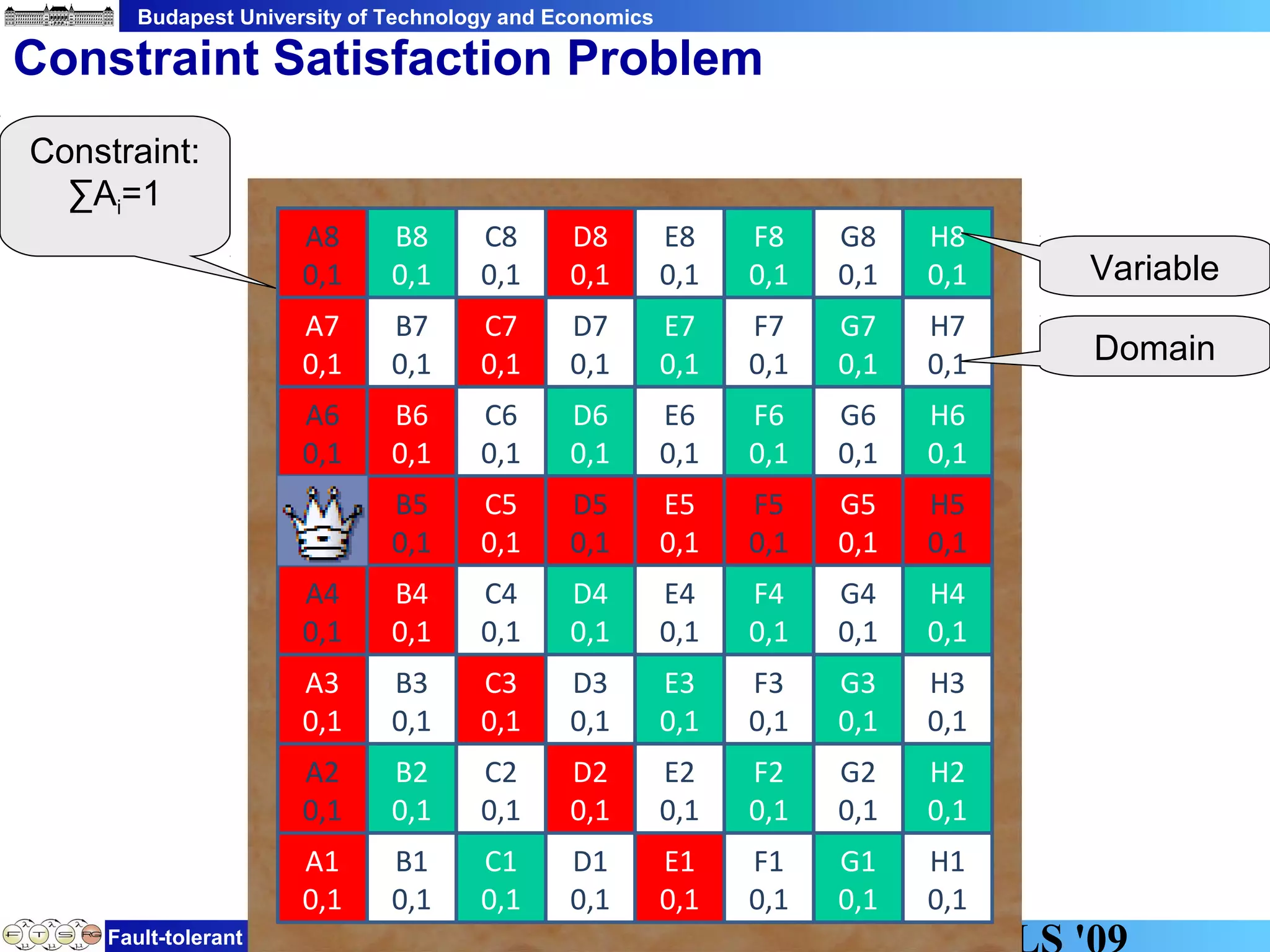
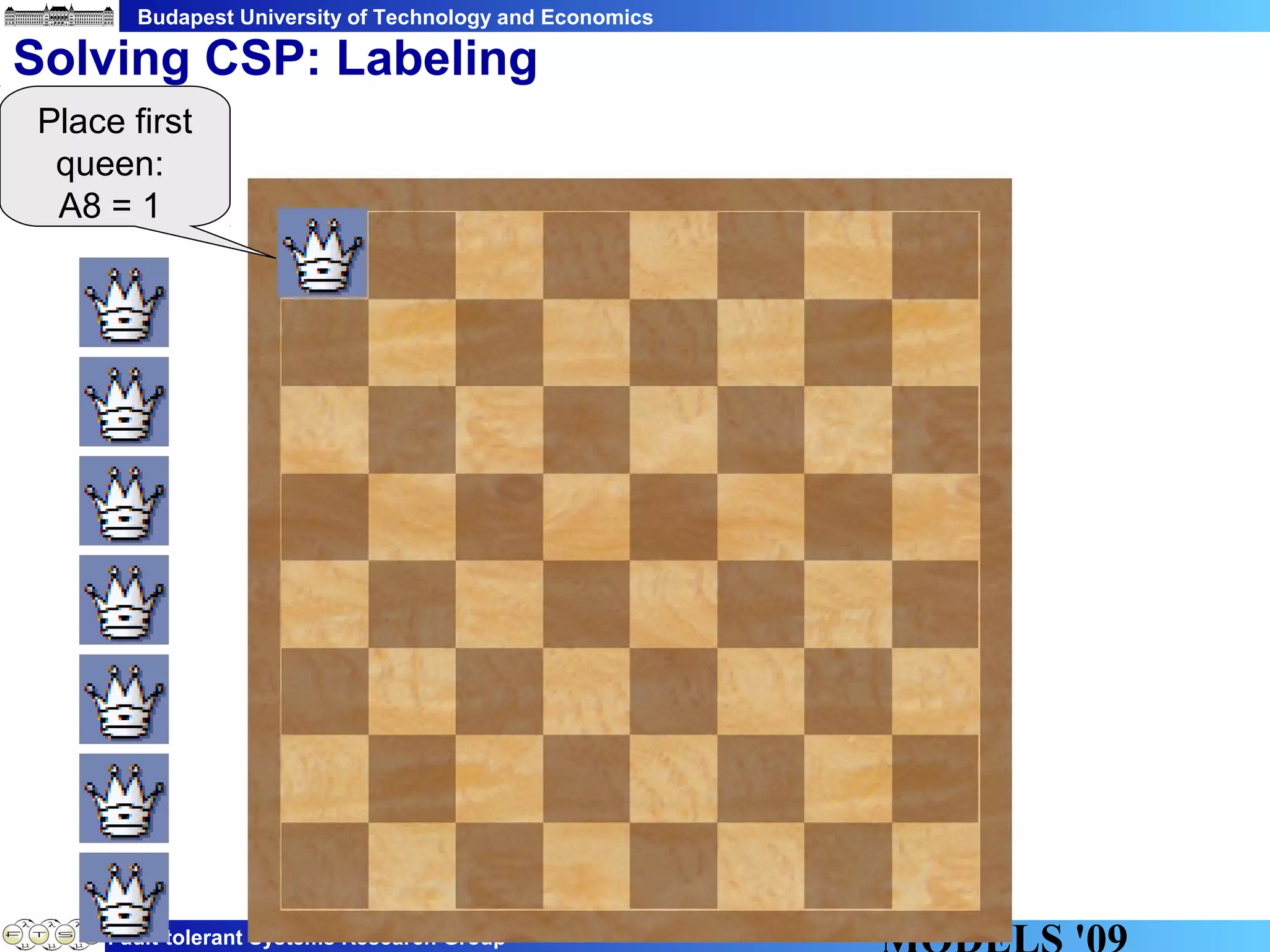
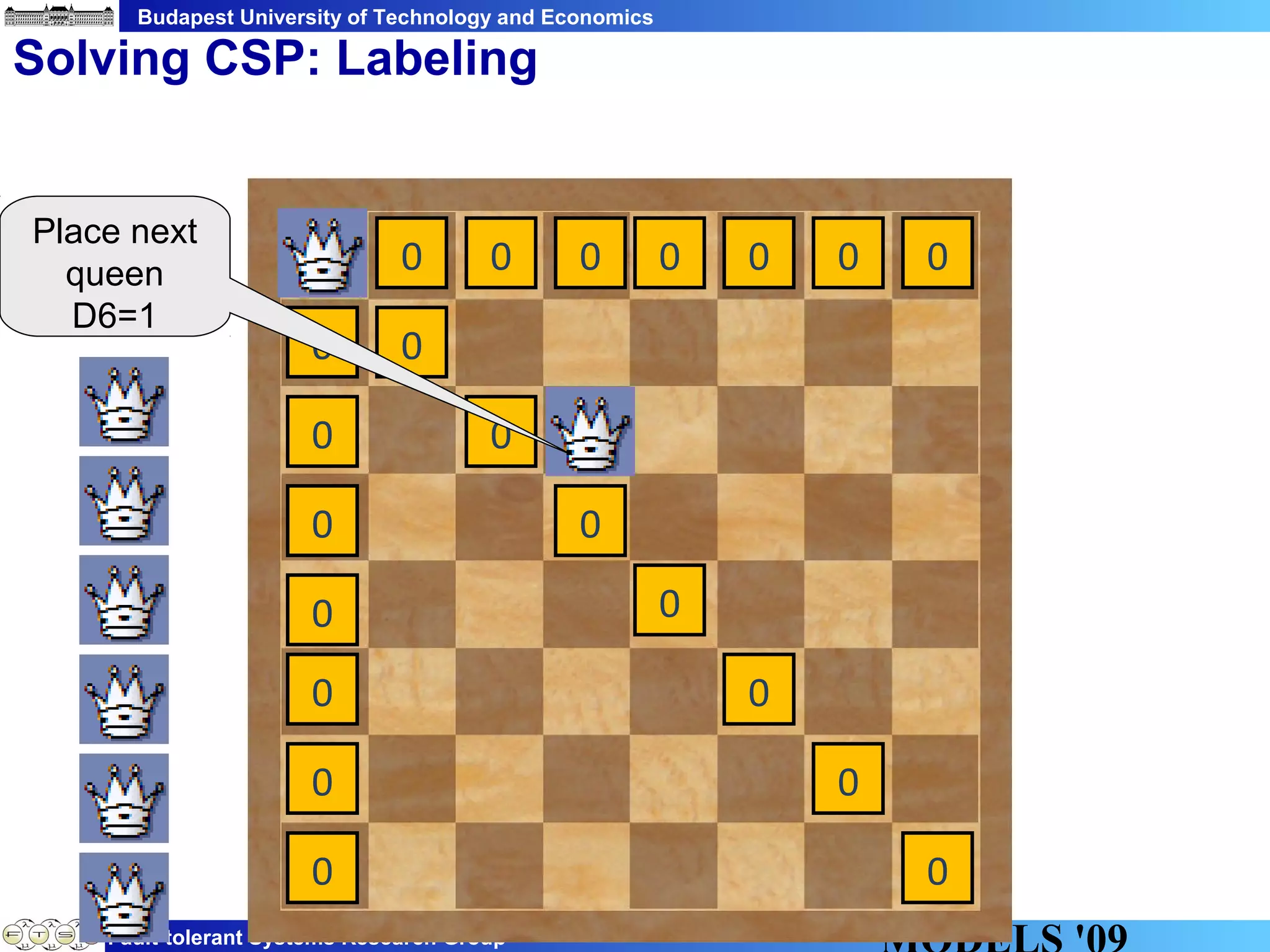
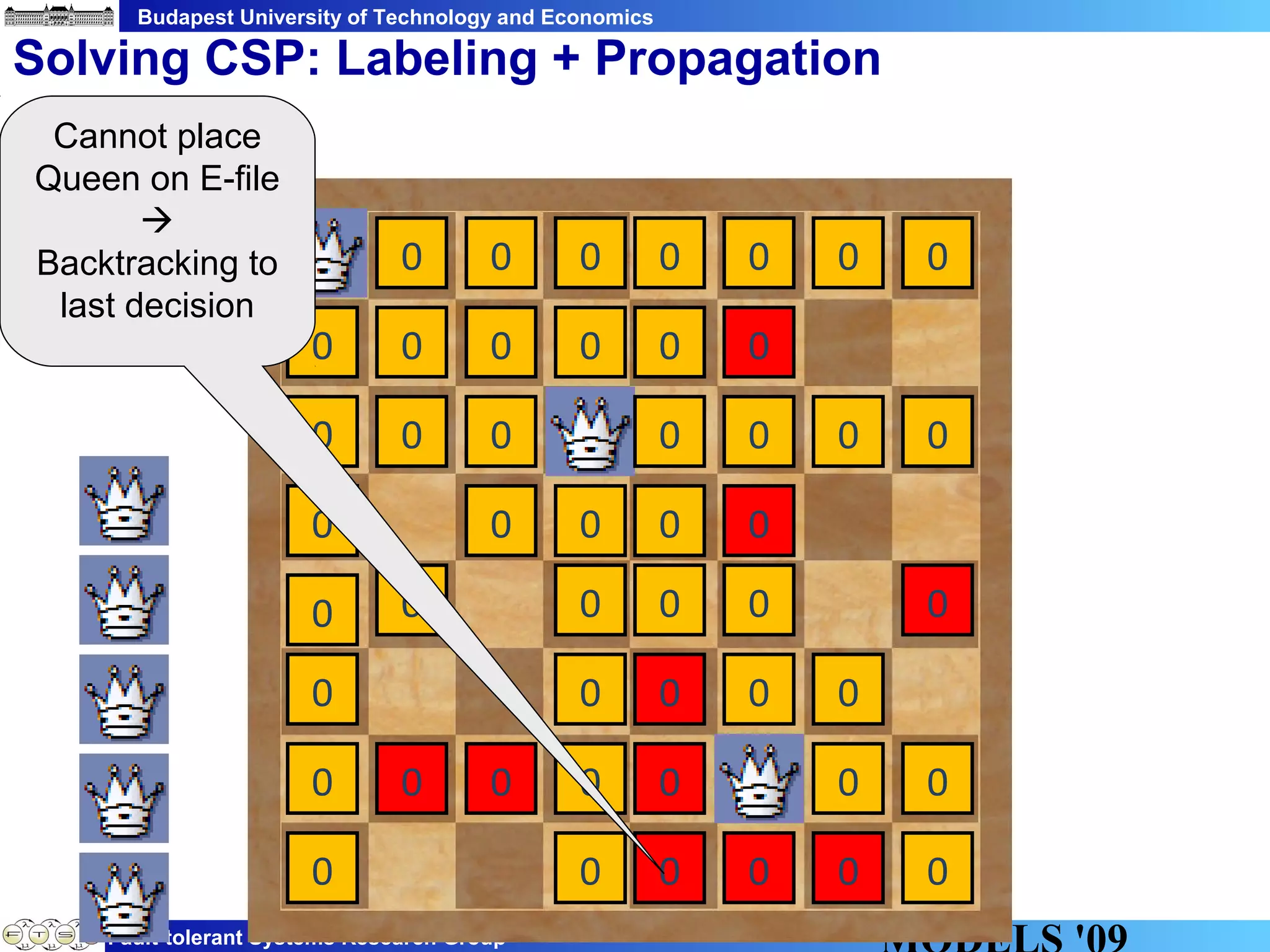
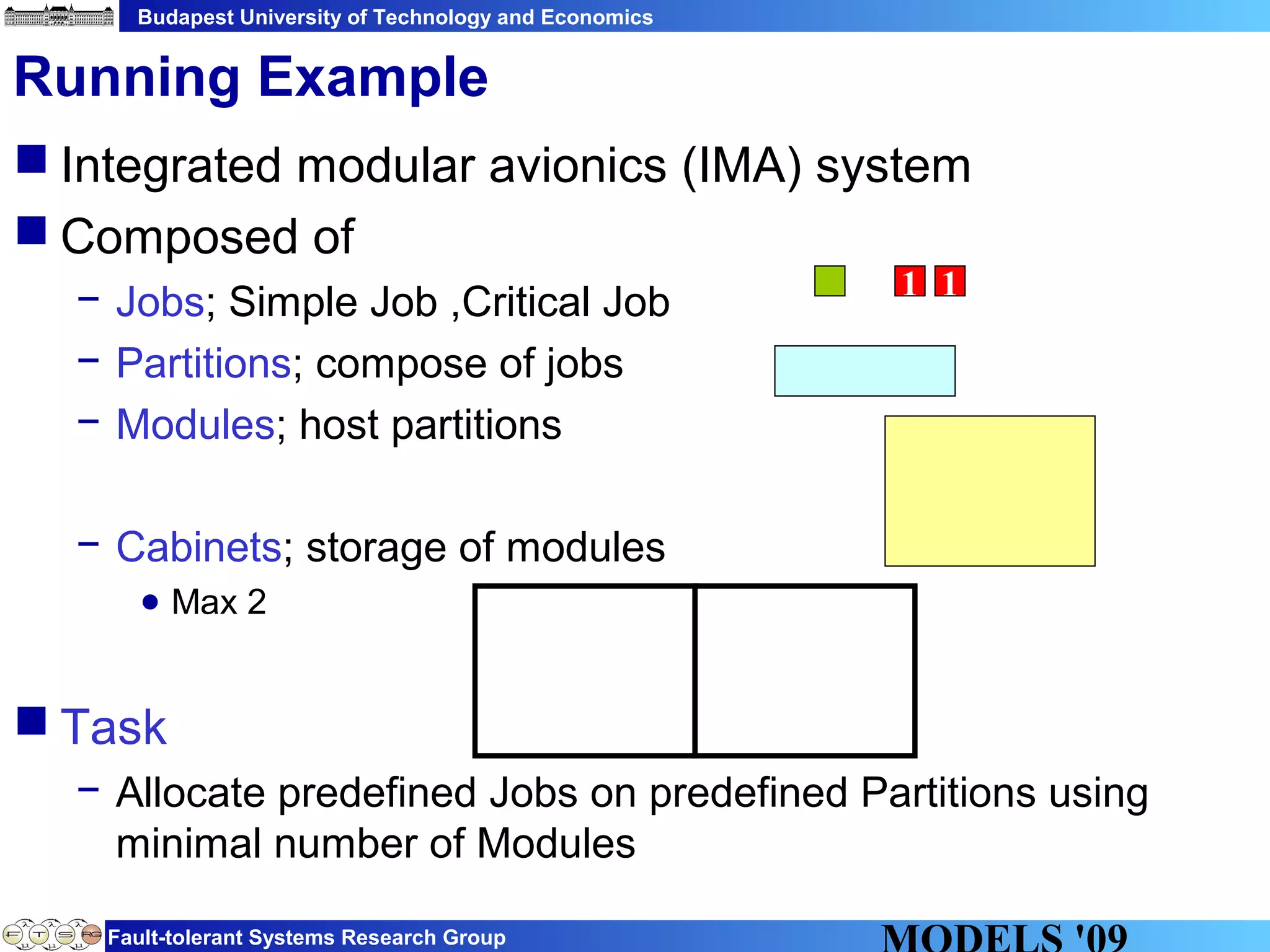
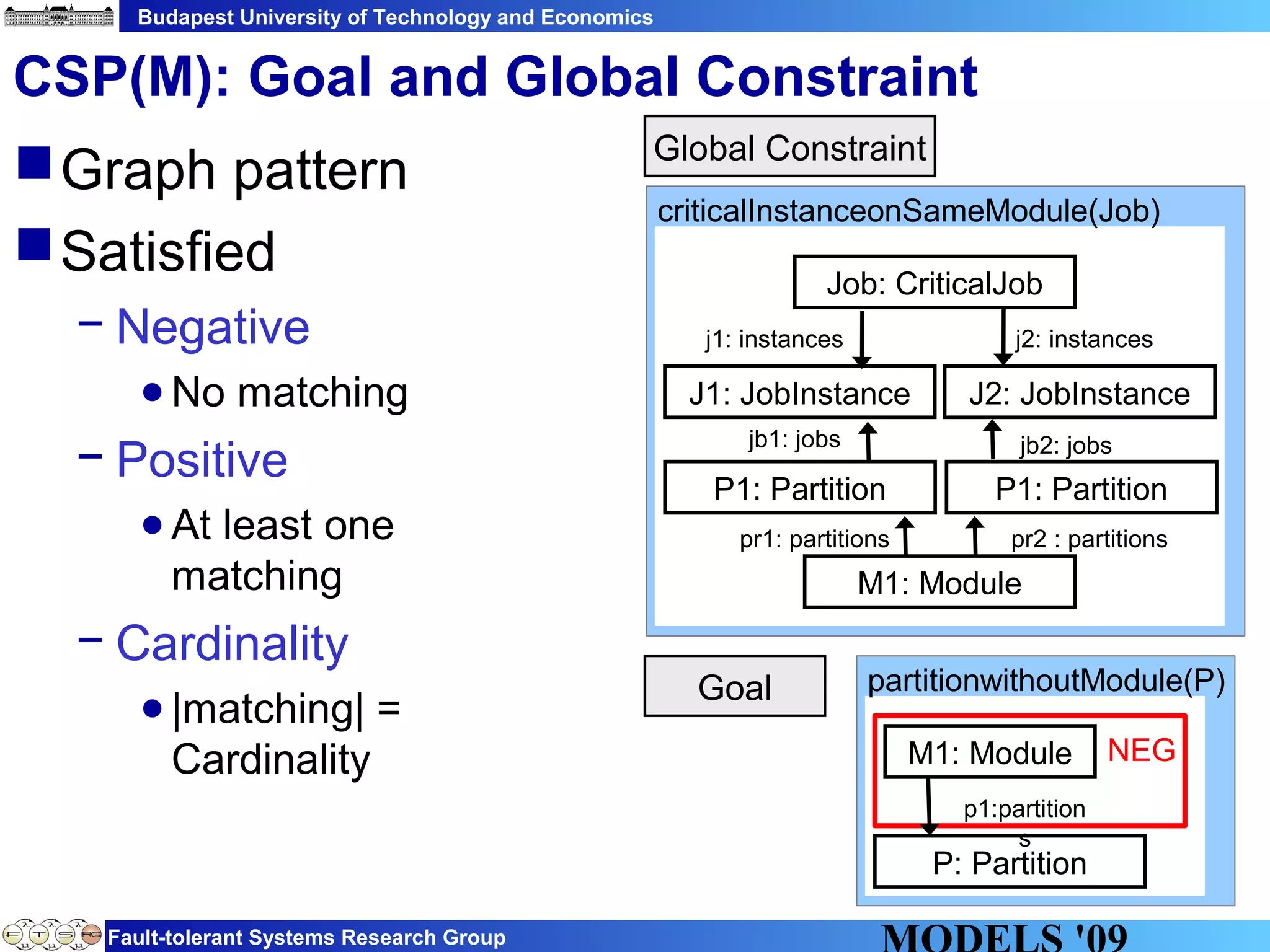
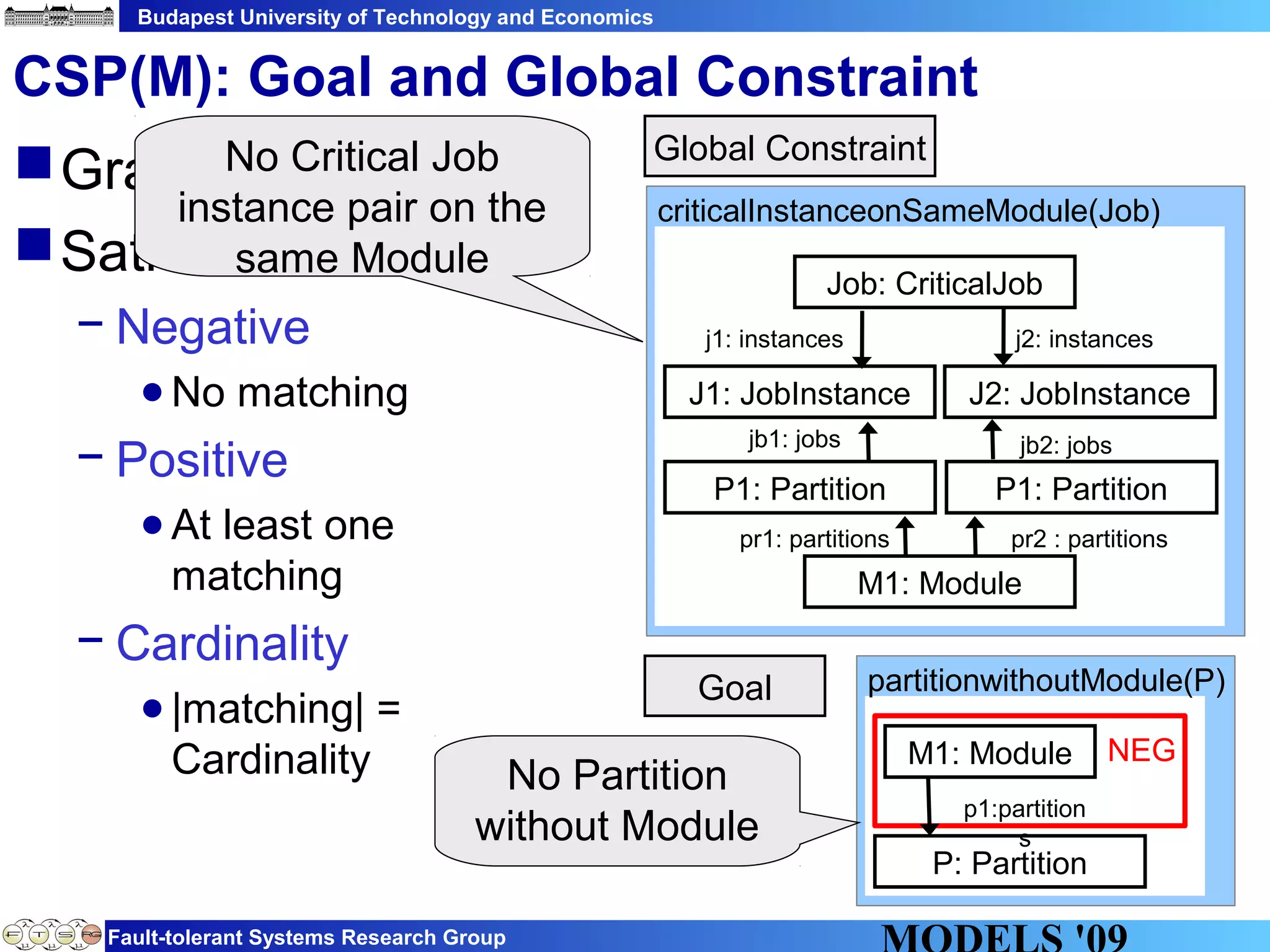
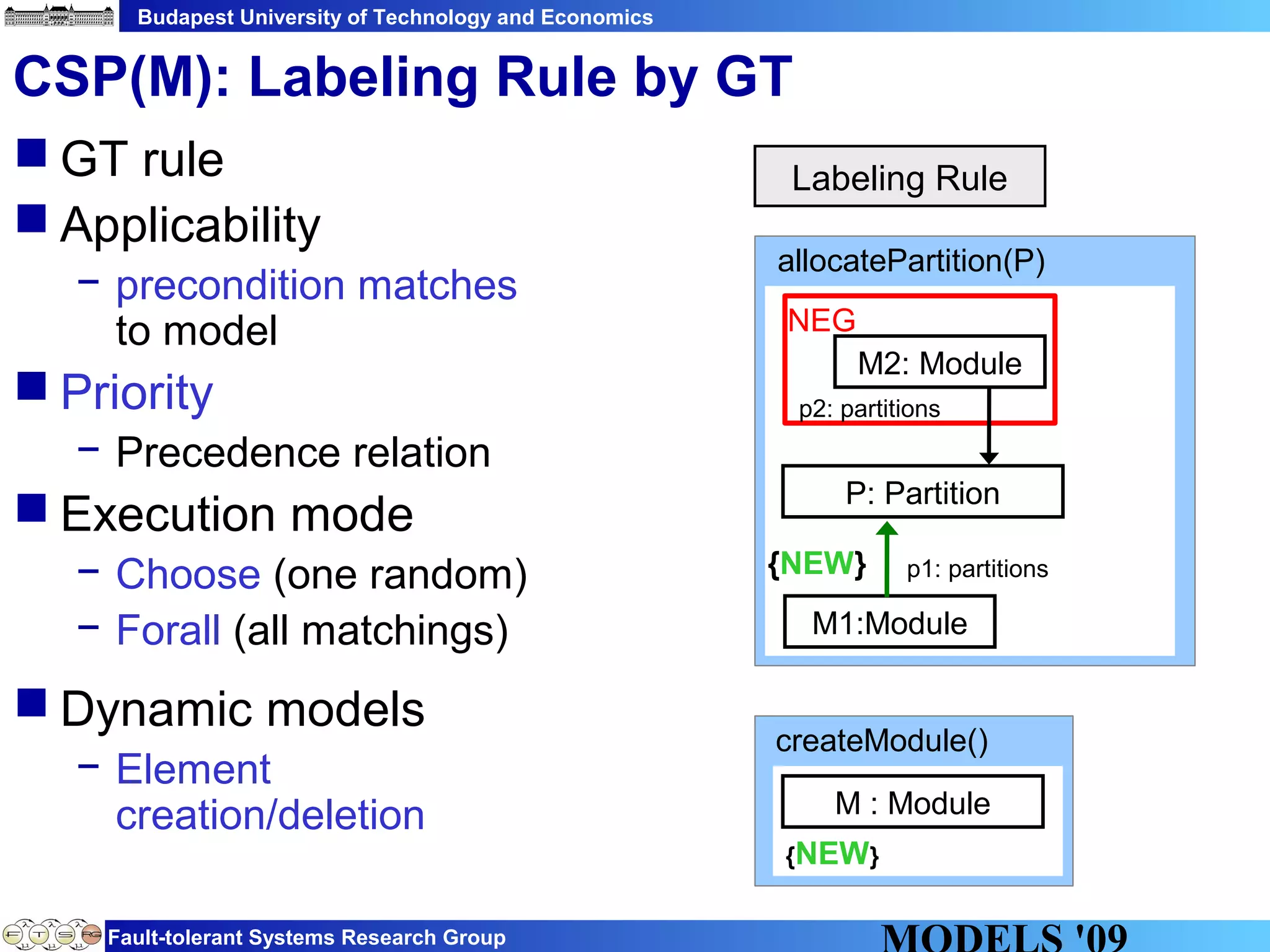
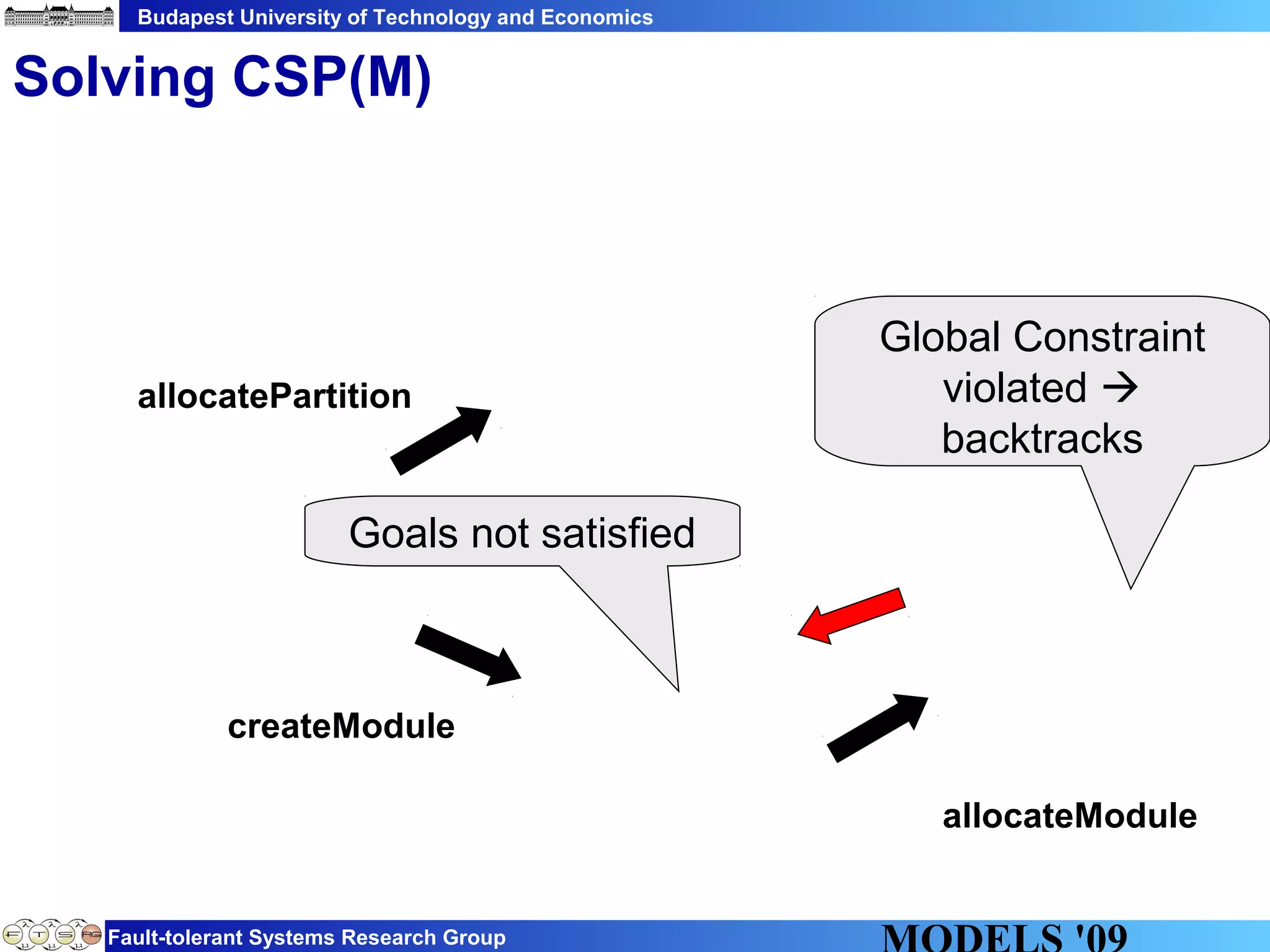
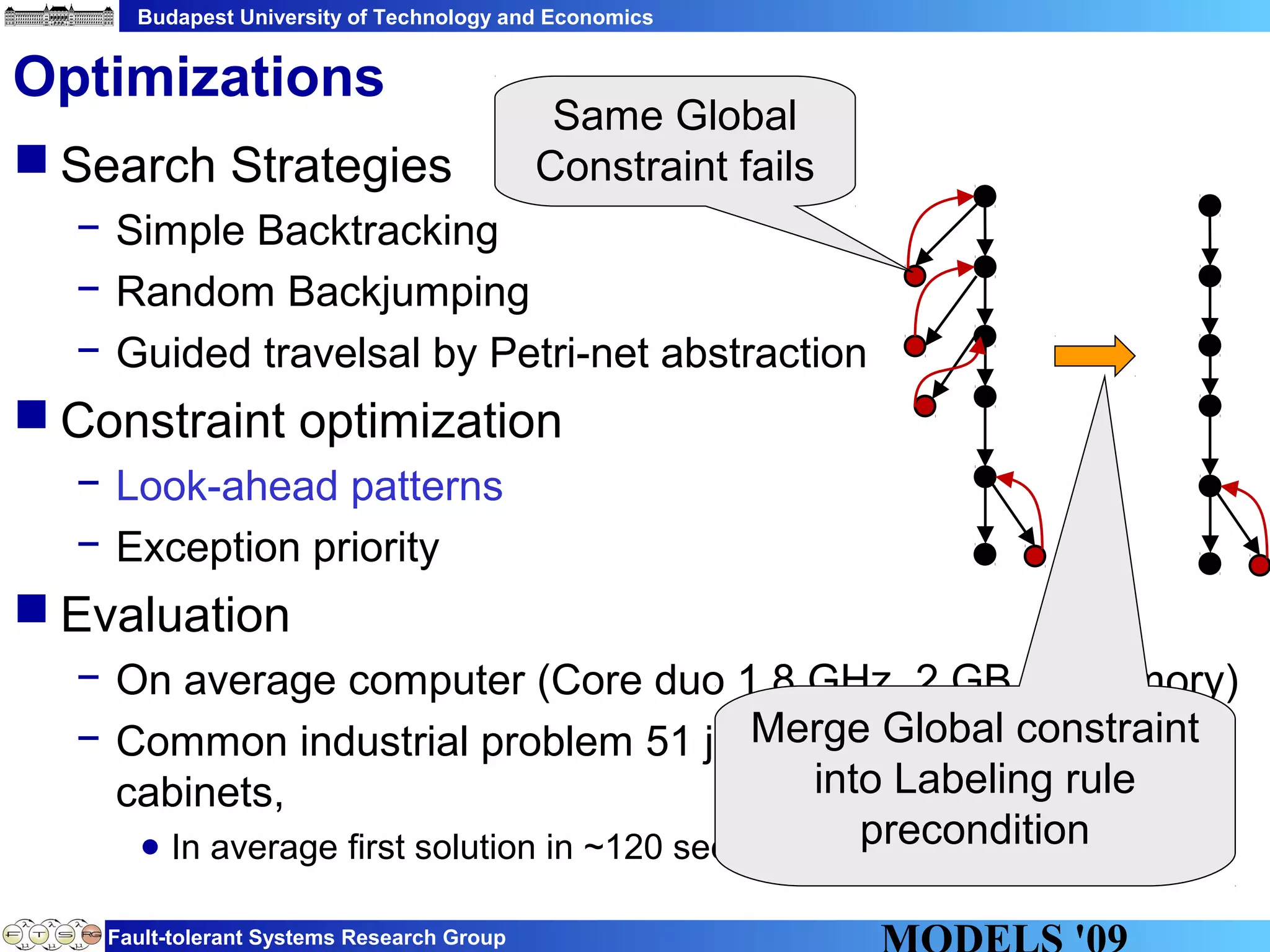
This document discusses constraint satisfaction problems over models (CSP(M)). It defines CSP(M) as being described by an initial model, a set of global constraints, goals, and labeling rules. It presents an example of allocating jobs to partitions in an integrated modular avionics system. Constraints and goals are defined as graph patterns. Labeling rules are defined using graph transformation rules. Solving CSP(M) involves applying labeling rules to reach a state satisfying all constraints and goals, backtracking if needed. The document outlines an implementation over VIATRA2 and discusses optimizations and future work.
More Related Content
Similar to CPS(M): Constraint Satisfaction Problem over Models (a.k.a rule based design space exploration)
CPS(M): Constraint Satisfaction Problem over Models (a.k.a rule based design space exploration)
- 1. Budapest University ofTechnology and Economics Fault-tolerant Systems Research Group CSP(M): Constraint Satisfaction Problem over Models Ákos Horváth and Dániel Varró
- 2. Budapest University ofTechnology and Economics Fault-tolerant Systems Research Group 2 Outline Introduction CSP(M) Conclusion Solving CSP(M)
- 3. Budapest University ofTechnology and Economics Fault-tolerant Systems Research Group Eight Queens Problem Place 8 queens on a checkboard without captures
- 4. Budapest University ofTechnology and Economics Fault-tolerant Systems Research Group Constraint Satisfaction Problem B8 0,1 A8 0,1 D8 0,1 C8 0,1 F8 0,1 E8 0,1 H8 0,1 G8 0,1 C7 0,1 B7 0,1 E7 0,1 D7 0,1 G7 0,1 F7 0,1 A7 0,1 H7 0,1 B6 0,1 A6 0,1 D6 0,1 C6 0,1 F6 0,1 E6 0,1 H6 0,1 G6 0,1 C5 0,1 B5 0,1 E5 0,1 D5 0,1 G5 0,1 F5 0,1 A5 0,1 H5 0,1 B4 0,1 A4 0,1 D4 0,1 C4 0,1 F4 0,1 E4 0,1 H4 0,1 G4 0,1 C3 0,1 B3 0,1 E3 0,1 D3 0,1 G3 0,1 F3 0,1 A3 0,1 H3 0,1 B2 0,1 A2 0,1 D2 0,1 C2 0,1 F2 0,1 E2 0,1 H2 0,1 G2 0,1 C1 0,1 B1 0,1 E1 0,1 D1 0,1 G1 0,1 F1 0,1 A1 0,1 H1 0,1 Constraint: ∑Ai=1 Variable Domain
- 5. Budapest University ofTechnology and Economics Fault-tolerant Systems Research Group Solving CSP: Labeling Place first queen: A8 = 1
- 6. Budapest University ofTechnology and Economics Fault-tolerant Systems Research Group Solving CSP: Constraint Propagation 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 Deduce consequences A7=0
- 7. Budapest University ofTechnology and Economics Fault-tolerant Systems Research Group Solving CSP: Labeling 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 Place next queen D6=1
- 8. Budapest University ofTechnology and Economics Fault-tolerant Systems Research Group Solving CSP: Constraint Propagation 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 Deduce consequence B6=0
- 9. Budapest University ofTechnology and Economics Fault-tolerant Systems Research Group Solving CSP: Labeling + Propagation 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 Cannot place Queen on E-file Backtracking to last decision
- 10. Budapest University ofTechnology and Economics Fault-tolerant Systems Research Group Solving CSP: Backtracking 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
- 11. Budapest University ofTechnology and Economics Fault-tolerant Systems Research Group Solving CSP: Labeling + Propagation 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
- 12. Budapest University ofTechnology and Economics Fault-tolerant Systems Research Group Solving CSP: Labeling + Propagation 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 If you are smarter, you can see this is in wrong place Backjumping to preceding state
- 13. Budapest University ofTechnology and Economics Fault-tolerant Systems Research Group Solving CSP: Backjumping 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 Continues with labeling…
- 14. Budapest University ofTechnology and Economics Fault-tolerant Systems Research Group Extensions: Dynamic variables 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 I5 0,1 I6 0,1 I3 0,1 I4 0,1 I2 0,1 Introducing new variables while solving
- 15. Budapest University ofTechnology and Economics Fault-tolerant Systems Research Group Extensions: Complex labeling 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 How many queens can you place without captures?
- 16. Budapest University ofTechnology and Economics Fault-tolerant Systems Research Group Extensions: Complex labeling 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
- 17. Budapest University ofTechnology and Economics Fault-tolerant Systems Research Group Extensions: Complex labeling 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 Placing a new queen invalidates effects of previous constraint propagation
- 18. Budapest University ofTechnology and Economics Fault-tolerant Systems Research Group Challenges for CSP over Models Dynamic variables Dynamic constraint management Native representation for (graph) models
- 19. Budapest University ofTechnology and Economics Fault-tolerant Systems Research Group 19 Outline Introduction CSP(M) Conclusion Solving CSP(M)
- 20. Budapest University ofTechnology and Economics Fault-tolerant Systems Research Group CSP(M) Described by (M0,C,G,L) − M0 initial model (typed graph) − C set of global constraints (graph patterns) − G set of goals (graph patterns) − L set of labeling rules (GT rules) Goal − Find a model Ms which satisfies all global constraints and goals. ●One model ●All model ●Optimal model
- 21. Budapest University ofTechnology and Economics Fault-tolerant Systems Research Group Integrated modular avionics (IMA) system Composed of − Jobs; Simple Job ,Critical Job − Partitions; compose of jobs − Modules; host partitions − Cabinets; storage of modules ● Max 2 Task − Allocate predefined Jobs on predefined Partitions using minimal number of Modules Running Example 1 1
- 22. Budapest University ofTechnology and Economics Fault-tolerant Systems Research Group Running Example: Constraints Partition one criticality level Critical job’s redundant instances on different Partitions and Modules Free memory of partition can not be less than zero ●Attribute constraint 1 1 1 1 12
- 23. Budapest University ofTechnology and Economics Fault-tolerant Systems Research Group CSP(M): Goal and Global Constraint Graph pattern Satisfied − Negative ●No matching − Positive ●At least one matching − Cardinality ●|matching| = Cardinality criticalInstanceonSameModule(Job) J1: JobInstance Job: CriticalJob j1: instances J2: JobInstance M1: Module j2: instances pr1: partitions jb1: jobs P1: Partition P1: Partition jb2: jobs pr2 : partitions partitionwithoutModule(P) P: Partition M1: Module NEG p1:partition s Global Constraint Goal
- 24. Budapest University ofTechnology and Economics Fault-tolerant Systems Research Group CSP(M): Goal and Global Constraint Graph pattern Satisfied − Negative ●No matching − Positive ●At least one matching − Cardinality ●|matching| = Cardinality criticalInstanceonSameModule(Job) J1: JobInstance Job: CriticalJob j1: instances J2: JobInstance M1: Module j2: instances pr1: partitions jb1: jobs P1: Partition P1: Partition jb2: jobs pr2 : partitions partitionwithoutModule(P) P: Partition M1: Module NEG p1:partition s Global Constraint Goal No Critical Job instance pair on the same Module No Partition without Module
- 25. Budapest University ofTechnology and Economics Fault-tolerant Systems Research Group CSP(M): Labeling Rule by GT GT rule Applicability − precondition matches to model Priority − Precedence relation Execution mode − Choose (one random) − Forall (all matchings) M1:Module allocatePartition(P) P: Partition M2: Module NEG p1: partitions{NEW} p2: partitions createModule() M : Module {NEW} Dynamic models − Element creation/deletion Labeling Rule
- 26. Budapest University ofTechnology and Economics Fault-tolerant Systems Research Group 26 Outline Introduction CSP(M) Conclusion Solving CSP(M)
- 27. Budapest University ofTechnology and Economics Fault-tolerant Systems Research Group Solving CSP(M) Current State
- 28. Budapest University ofTechnology and Economics Fault-tolerant Systems Research Group Solving CSP(M) allocatePartition Next state Transition New Elements
- 29. Budapest University ofTechnology and Economics Fault-tolerant Systems Research Group Solving CSP(M) allocatePartition Solution: Satisfies goals and global constraint
- 30. Budapest University ofTechnology and Economics Fault-tolerant Systems Research Group Solving CSP(M) allocatePartition createModule allocateModule Goals not satisfied Global Constraint violated backtracks
- 31. Budapest University ofTechnology and Economics Fault-tolerant Systems Research Group Implementation over VIATRA2 Incremental constraint evaluation by incremental pattern matching − Cached matchings − Incrementally updated Simple state space representation Typed graph comparison − DSMDiFF Backtracking − Transaction on atomic manipulation operations
- 32. Budapest University ofTechnology and Economics Fault-tolerant Systems Research Group Search Strategies − Simple Backtracking − Random Backjumping − Guided travelsal by Petri-net abstraction Constraint optimization − Look-ahead patterns − Exception priority Evaluation − On average computer (Core duo 1.8 GHz, 2 GB of memory) − Common industrial problem 51 jobs, 7 partitions and 4 cabinets, ● In average first solution in ~120 sec Optimizations
- 33. Budapest University ofTechnology and Economics Fault-tolerant Systems Research Group Search Strategies − Simple Backtracking − Random Backjumping − Guided travelsal by Petri-net abstraction Constraint optimization − Look-ahead patterns − Exception priority Evaluation − On average computer (Core duo 1.8 GHz, 2 GB of memory) − Common industrial problem 51 jobs, 7 partitions and 4 cabinets, ● In average first solution in ~120 sec Optimizations
- 34. Budapest University ofTechnology and Economics Fault-tolerant Systems Research Group Search Strategies − Simple Backtracking − Random Backjumping − Guided travelsal by Petri-net abstraction Constraint optimization − Look-ahead patterns − Exception priority Evaluation − On average computer (Core duo 1.8 GHz, 2 GB of memory) − Common industrial problem 51 jobs, 7 partitions and 4 cabinets, ● In average first solution in ~120 sec Optimizations
- 35. Budapest University ofTechnology and Economics Fault-tolerant Systems Research Group Search Strategies − Simple Backtracking − Random Backjumping − Guided travelsal by Petri-net abstraction Constraint optimization − Look-ahead patterns − Exception priority Evaluation − On average computer (Core duo 1.8 GHz, 2 GB of memory) − Common industrial problem 51 jobs, 7 partitions and 4 cabinets, ● In average first solution in ~120 sec Optimizations Restriction on the number of rule applications
- 36. Budapest University ofTechnology and Economics Fault-tolerant Systems Research Group Search Strategies − Simple Backtracking − Random Backjumping − Guided travelsal by Petri-net abstraction Constraint optimization − Look-ahead patterns − Exception priority Evaluation − On average computer (Core duo 1.8 GHz, 2 GB of memory) − Common industrial problem 51 jobs, 7 partitions and 4 cabinets, ● In average first solution in ~120 sec Optimizations Same Global Constraint fails Merge Global constraint into Labeling rule precondition
- 37. Budapest University ofTechnology and Economics Fault-tolerant Systems Research Group Search Strategies − Simple Backtracking − Random Backjumping − Guided travelsal by Petri-net abstraction Constraint optimization − Look-ahead patterns − Exception priority Evaluation − On average computer (Core duo 1.8 GHz, 2 GB of memory) − Common industrial problem 51 jobs, 7 partitions and 4 cabinets, ● In average first solution in ~120 sec Optimizations
- 38. Budapest University ofTechnology and Economics Fault-tolerant Systems Research Group 38 Outline Introduction CSP(M) Conclusion Solving CSP(M)
- 39. Budapest University ofTechnology and Economics Fault-tolerant Systems Research Group Conclusion Summary − General definition of constraint problems over models ● Labeling rules by GT rules ● Goals and constraints by GT patterns ● Dynamic variables − Implementation over VIATRA2 ● Constraint propagation using incremental pattern matching ● Dynamically add/remove constraints and labeling rules Future work − Compact state space representation ● Model differentials ● Symbolic state representation ● State comparison − Automatic look-ahead pattern detection (critical pair analysis) − Comparison with Alloy and Korat
Editor's Notes
- #21 Global constraint must hold in all traversed state space Goals are need to be satisfied in the solution model Labeling rule defines the valid operations to use to reach a solution model
- #22 integrated modular avionics (IMA) system composed of Jobs (also referred as applications), Partitions, Modules and Cabinets. Jobs are the atomic software blocks of the system defined by their memory requirement. Based on their criticality level jobs are separated into two sets: critical and simple (non-critical). For critical jobs double or triple modular redundancy is applied while for simple ones only one instance is allowed. Partitions are complex software components composed of jobs with a predefined free memory space. Jobs can be allocated to the partition as long as they fit into its memory space. Modules are SW components capable of hosting partitions. Finally, Cabinets are storages for maximum up to two modules used to physically distribute elements of the system. Additionally a certain number of safety related requirements will also have to be satisfied: (i) a partition can only host jobs of one criticality level and (ii) instances of a certain critical job can not be allocated to the same partition and module. The task is to allocate an IMA system defined by its jobs and partitions over a predefined cabinet structure and to minimize the number of modules used.
- #32 Constraint evaluation. As matches of patterns are cached, this reduces the evaluation of constraints and preconditions of labeling rules to a simple check. This way, the solver has an incrementally maintained up-to-date view of its constraint store and enabled labeling rules.
- #33 Exception priority: restrict rule application
- #34 Exception priority: restrict rule application
- #35 Exception priority: restrict rule application
- #36 Exception priority: restrict rule application
- #37 Exception priority: restrict rule application
- #38 Exception priority: restrict rule application
- #42 For introducing GT related notation, I chose a Graph transformation requires a metamodel (or a type graph) that defines the abstract syntax of our modeling domain. Multiplicity declares the number of objects, that at run-time, may participate in an association. An instance model (or an instance graph) is also needed, which describes a concrete system from our domain.
- #44 Exception priority: restrict rule application
- #49 To traverse the search space of a constraint program introduced in Sec. 3.2, we define the solver as a virtual machine that maintains a 4-tuple (CG,CS,AM,LS) as a state. CG is called the current goal; CS is the constraint store; AM is the actual model; and finally LS is the labeling store. The (i) current goal stores the subgoals that still need to be satisfied; the (ii) constraint store holds all constraints the solver has satisfied so far while the (iii) actual model represents the underlying actual model and finally the (iv) labeling store contains all enabled labeling rules. An element in the labeling store is a pair (l,m), where l is a labeling rule and m is a valid match of its precondition LHSl in AM; formally m : LHSl −!AM. Initially, the CG, CS and LS are