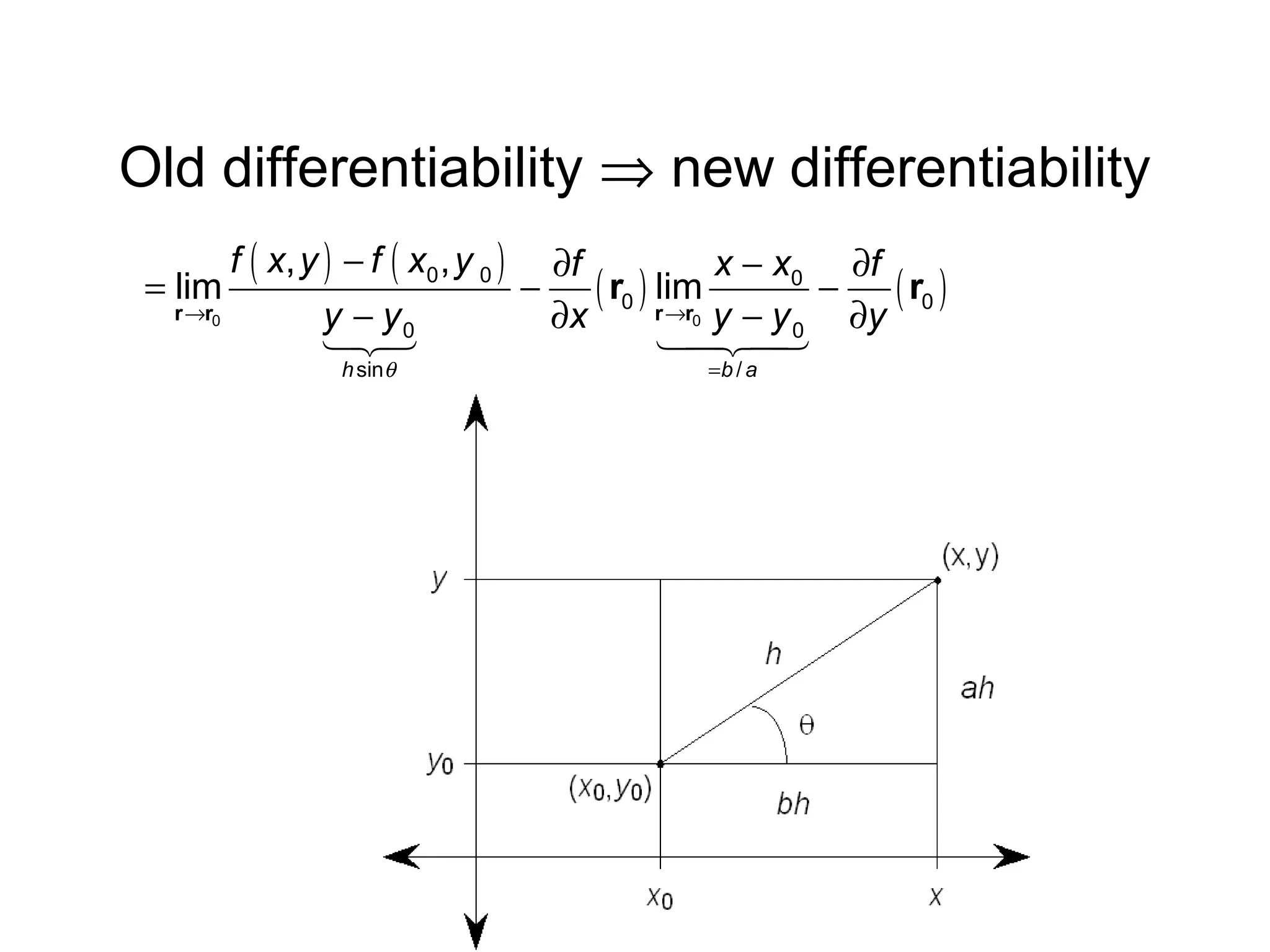
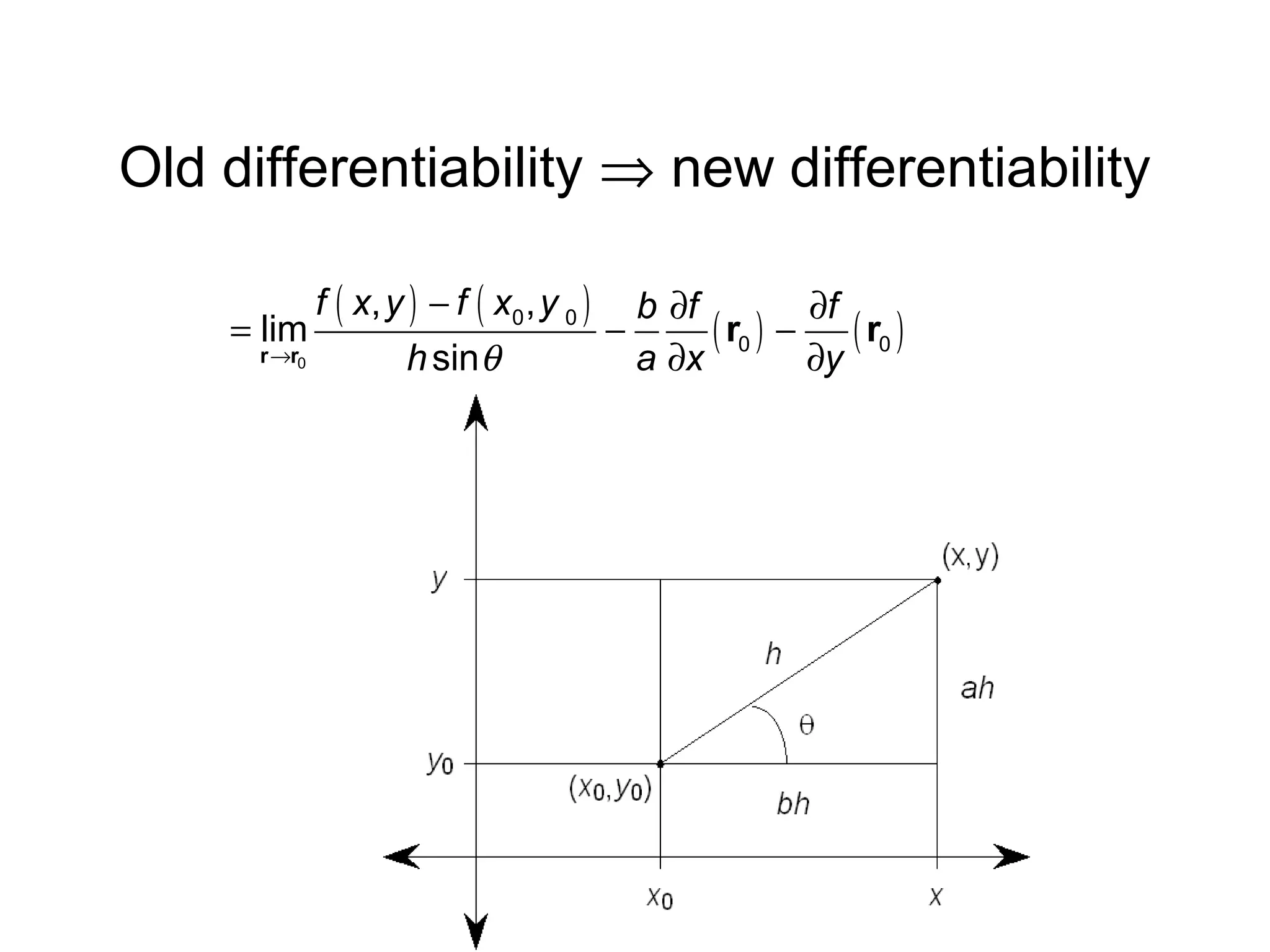
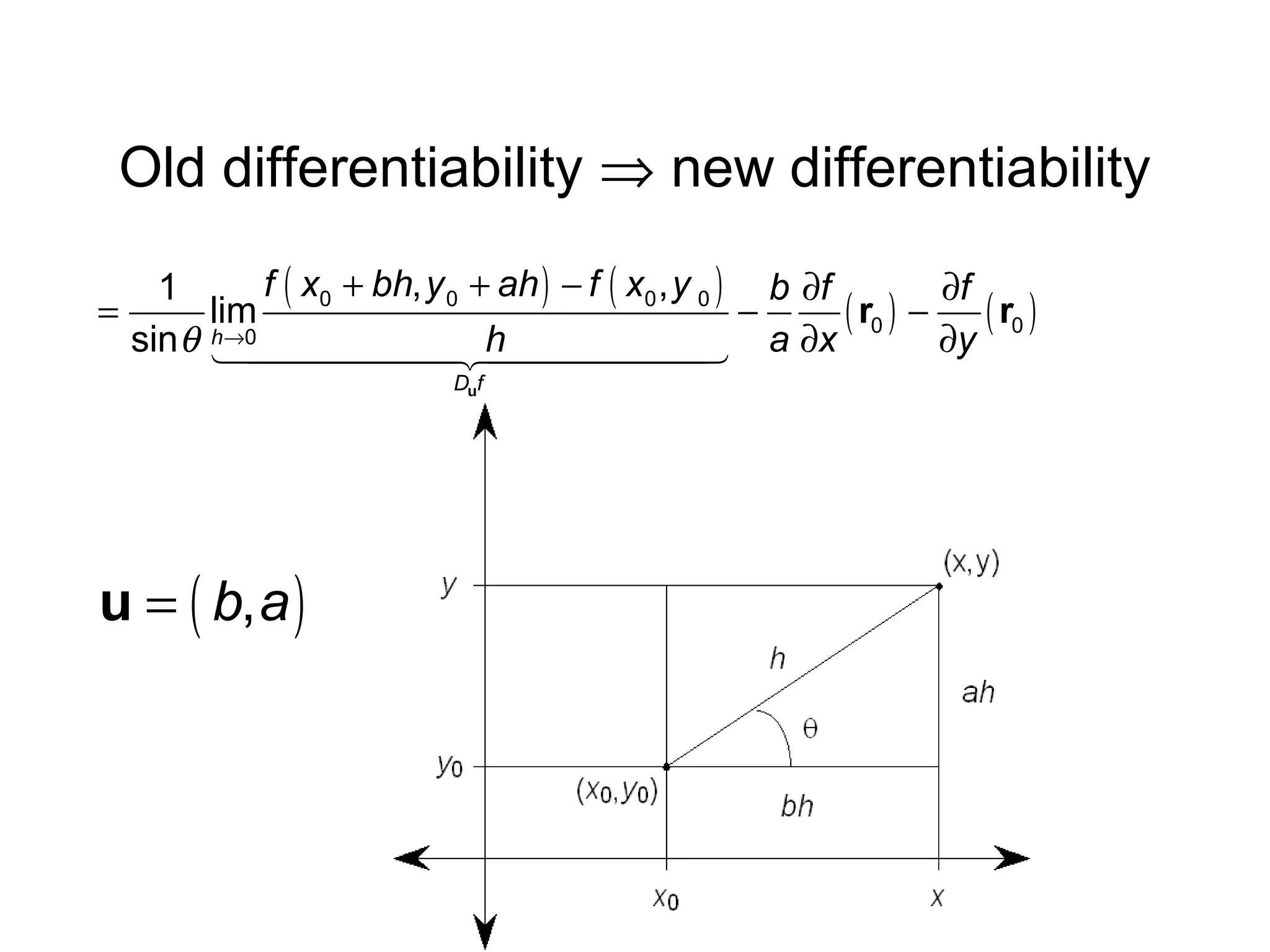
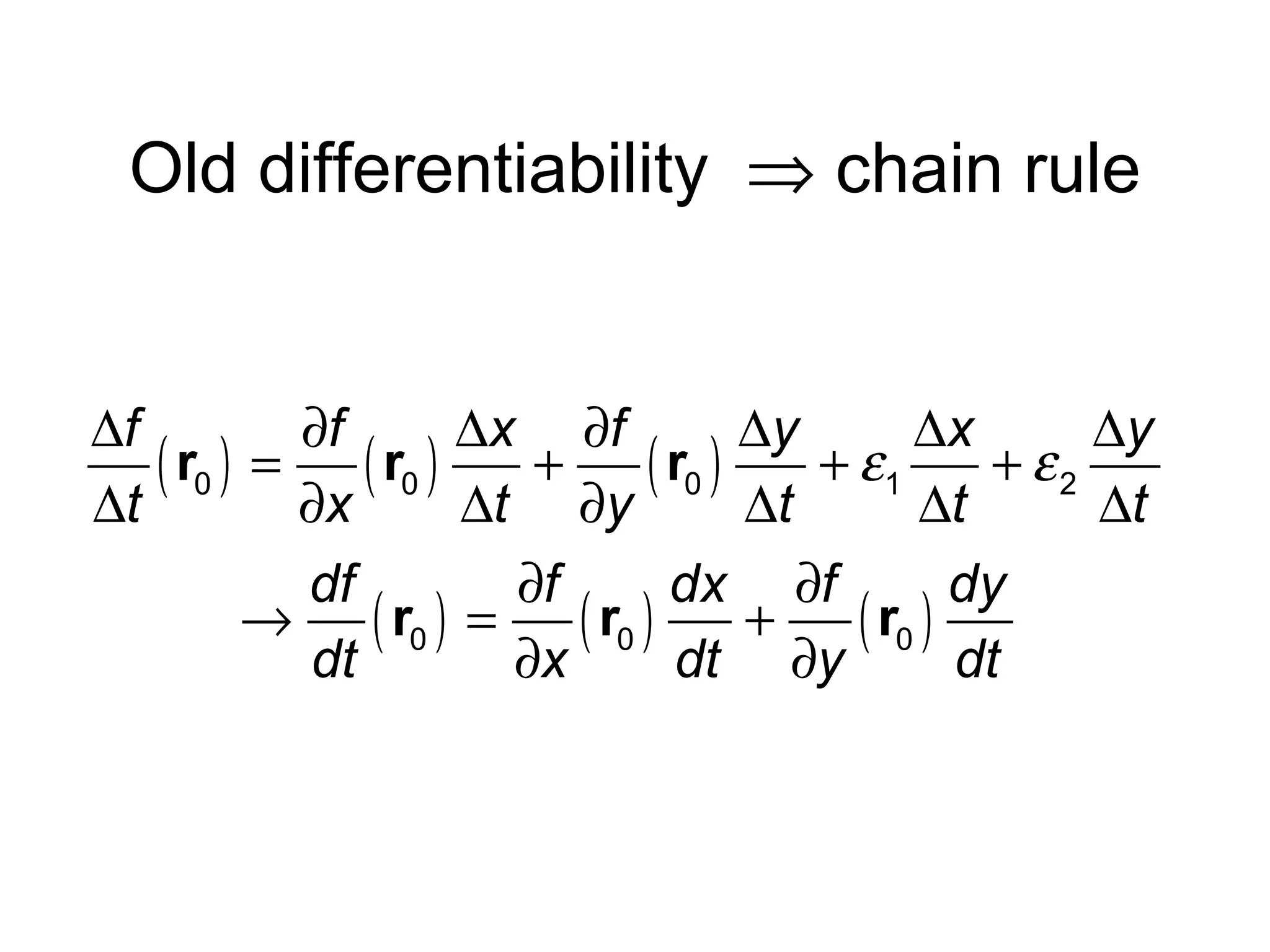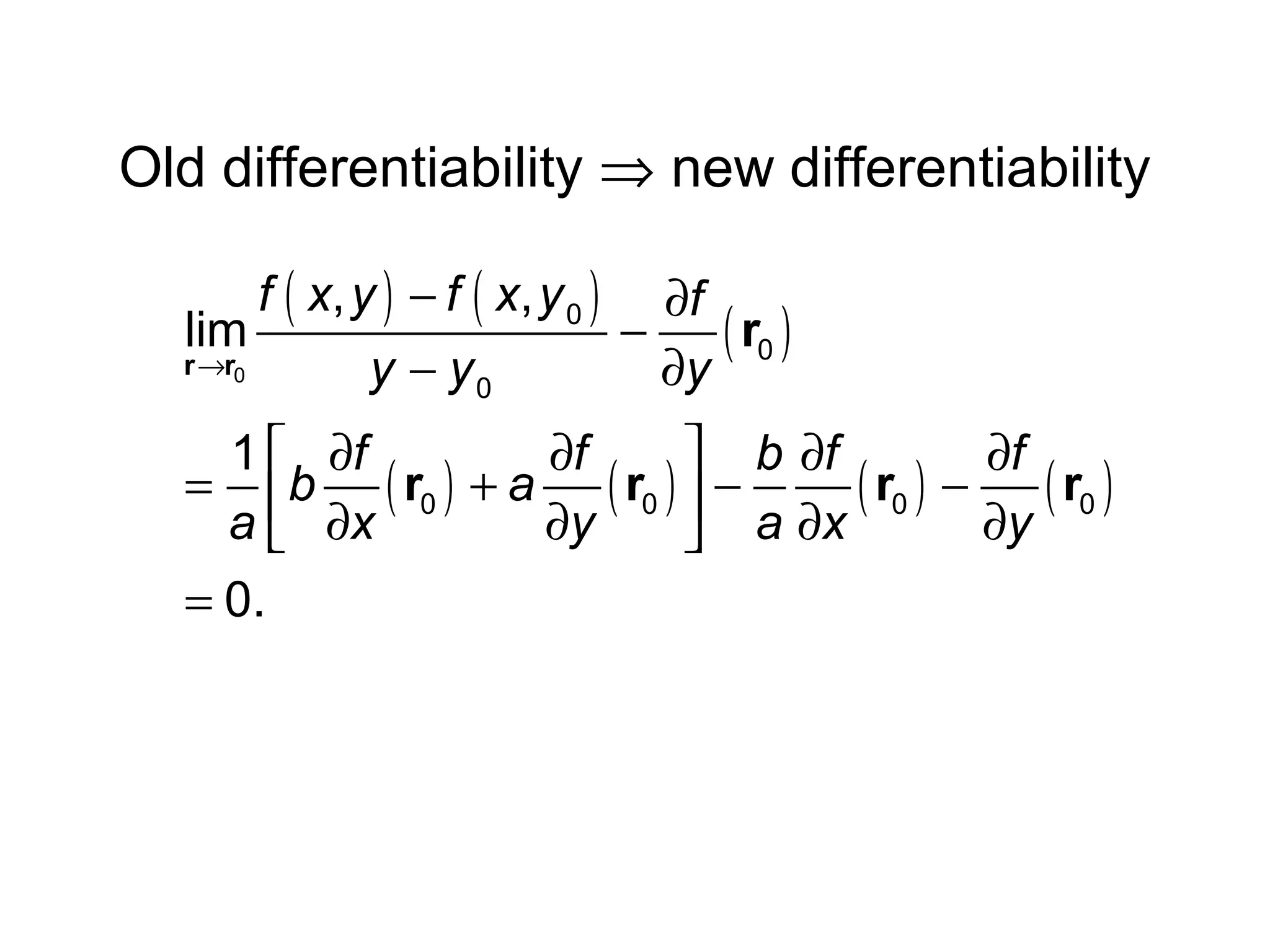This document presents an alternative proof of the chain rule for multivariable functions. It begins by defining the chain rule formula and then proves it using a new definition of differentiability. The proof shows that under the new definition, differentiability implies continuity and satisfies the chain rule. It also proves that the old definition of differentiability implies the new one, so both definitions are equivalent. The conclusion is that the old definition of differentiability is sufficient to prove the chain rule.

1. An alternative proof for the chain
rule for multivariable functions
Raymond Jensen
Northern State University

2. Chain rule: let f be differentiable wrt. x, y,
and x, y differentiable wrt. t.
x = x(t)
y = y (t)
f = f ( x, y )
df ∂f dx ∂f dy
=
+
dt ∂x dt ∂y dt

3. Proof
g ( t ) − g ( t0 )
dg
( t0 ) = lim
t →t0
dt
t − t0
f ( x ( t ) ,y ( t ) ) = g ( t )
=g ( t )
df
( x ( t0 ) , y ( t0 ) ) = lim0
t →t
dt
=g ( t0 )
64 744 64 744
4
8
4
8
f ( x ( t ) , y ( t ) ) − f ( x ( t0 ) , y ( t0 ) )
t − t0

4. Proof: begin as with the product
rule
df
df
x ( t0 ) , y ( t0 ) ) =
( r0 )
(
dt
dt
f ( x ( t ) , y ( t ) ) − f ( x ( t0 ) , y ( t ) ) + f ( x ( t0 ) , y ( t ) ) − f ( x ( t0 ) , y ( t0 ) )
= lim
t →t0
t − t0
= lim
t →t0
f ( x ( t ) , y ( t ) ) − f ( x ( t0 ) , y ( t ) )
t − t0
+ lim
t →t0
f ( x ( t0 ) , y ( t ) ) − f ( x ( t0 ) , y ( t 0 ) )
t − t0

5. Proof: continue as with the
single-variable chain rule
f ( x ( t ) , y ( t ) ) − f ( x ( t0 ) , y ( t ) ) x ( t ) − x ( t0 )
df
( r0 ) = lim
t →t0
dt
x ( t ) − x ( t0 )
t − t0
f ( x ( t0 ) , y ( t ) ) − f ( x ( t0 ) , y ( t0 ) ) y ( t ) − y ( t0 )
+ lim
t →t0
y ( t ) − y ( t0 )
t − t0
f ( x, y ) − f ( x0 , y )
x ( t ) − x ( t0 )
= lim
lim
r →r0
t →t0
x − x0
t − t0
f ( x0 , y ) − f ( x 0 , y 0 )
y ( t ) − y ( t0 )
+ lim
lim
r →r0
t →t0
y − y0
t − t0

6. Proof: continue as with the
single-variable chain rule
f ( x, y ) − f ( x 0 , y )
x ( t ) − x ( t0 )
df
lim
( r0 ) = rlim
→r0
t →t0
dt
x − x0
t − t0
144424443 144
244
3
="
∂f
"
∂x
=
dx
dt
f ( x0 , y ) − f ( x0 , y 0 )
y ( t ) − y ( t0 )
+ lim
lim
r →r0
t →t0
y − y0
t − t0
1444 24444 144244
4
3
3
=
∂f
∂y
=
dy
dt

7. Definition: f is [new] differentiable at r0 if
f ( x, y ) − f ( x0 , y ) ∂f
lim
=
( r0 )
r →r0
x − x0
∂x
and
f ( x, y ) − f ( x, y 0 ) ∂f
lim
=
( r0 )
r →r0
y − y0
∂y

8. Definition: f is [old] differentiable at r0 if
∆f ( r0 ) = f ( r0 + ∆r ) − f ( r0 )
∂f
∂f
=
( r0 ) ∆x + ( r0 ) ∆y + ε1∆x + ε 2∆y
∂x
∂y
where ε1 = ε 1 ( ∆r ) , ε 2 = ε 2 ( ∆r ) → 0 as ∆r → 0
∆x = x − x0 , ∆y = y − y 0 , ∆r = r − r0

9. Old differentiability ⇒ chain rule
∆f
∂f
∆x ∂f
∆y
∆x
∆y
( r0 ) = ( r0 ) + ( r0 ) + ε1 + ε 2
∆t
∂x
∆t ∂y
∆t
∆t
∆t
df
∂f
dx ∂f
dy
→ ( r0 ) =
( r0 ) + ( r0 )
dt
∂x
dt ∂y
dt

10. Old differentiability ⇒ continuity
• Leithold thm. 12.4.3

11. New differentiability ⇒ continuity
lim f ( r ) − f ( r0 ) = lim f ( x, y ) − f ( x, y 0 ) + f ( x, y 0 ) − f ( x0 , y 0 ) 


r →r0
r →r0
= lim f ( x, y ) − f ( x, y 0 )  + lim f ( x, y 0 ) − f ( x0 , y 0 ) 




r →r0
r →r0
 f ( x, y ) − f ( x , y 0 ) 
= lim 
lim
 r →r0 ( y − y 0 )
r →r0
y − y0

1444 24444 14243
4
3
=0
=
∂f
∂y
 f ( x, y 0 ) − f ( x0 , y 0 ) 
+ lim 
lim
 r →r0 ( x − x0 )
r →r0
x − x0

14444
24444  14243
3
=0
=
=0
∂f
∂x

12. If partials of f exist near r0 and are continuous
at r0 then f is old differentiable at r0.
• Stewart thm. 11.4.8, Leithold thm. 12.4.4

13. If partials of f exist near r0 and are continuous
at r0 then f is new differentiable at r0.
f ( x, y ) − f ( x0 , y ) ∂f
f ( x, y ) − f ( x 0 , y )
f ( x, y 0 ) − f ( x 0 , y 0 )
lim
−
− lim
( r0 ) = rlim
r →r0
→r0
r →r0
x − x0
∂x
x − x0
x − x0
( )
678 6 74 6 74 6 74
4( 0 )8 4 ( ) 8
4( 0 ) 8
f ( x, y ) − f ( x 0 , y ) − f ( x , y 0 ) + f ( x 0 , y 0 )
= lim
r →r0
x − x0
g x
g x
h x
g ( x ) − g ( x0 ) −  h ( x ) − h ( x 0 ) 


= lim
r →r0
x − x0
MVT
h x

14. If partials exist near r0 and are continuous at
r0 then f is new differentiable at r0.
f ( x, y ) − f ( x0 , y ) ∂f
g ′ ( u ) ∆x − h′ ( v ) ∆x
lim
−
( r0 ) = rlim
r →r0
→r0
x − x0
∂x
∆x
= lim g ′ ( u ) − h′ ( v ) 


r →r0
∂f
∂f
= lim ( u, y ) − lim ( v , y 0 )
r →r0 ∂x
r →r0 ∂x
∂f
∂f
=
( r0 ) − ( r0 )
∂x
∂x
=0

15. Old differentiability ⇒ new differentiability
f ( x, y ) − f ( x, y 0 ) ∂f
lim
−
( r0 )
r →r0
y − y0
∂y
f ( x, y ) − f ( x, y 0 ) − f ( x0 , y ) + f ( x0 , y 0 )
= lim
r →r0
y − y0
f ( x, y ) − f ( x0 , y 0 ) − f ( x, y 0 ) − f ( x0 , y ) + 2f ( x0 , y 0 )
= lim
r →r0
y − y0
f ( x, y ) − f ( x 0 , y 0 )
f ( x 0 , y 0 ) − f ( x, y 0 )
f ( x0 , y 0 ) − f ( x0 , y )
= lim
+ lim
+ lim
r →r0
r →r0
r →r0
y − y0
y − y0
y − y0
1444 24444
4
3
=−
∂f
∂y
f ( x, y ) − f ( x 0 , y 0 )
f ( x 0 , y 0 ) − f ( x, y 0 )
x − x0 ∂f
= lim
+ lim
lim
−
( r0 )
r →r0
r →r0
r →r0 y − y
y − y0
x − x0
∂y
0
1444 24444
4
3
=−
∂f
∂x

16. Old differentiability ⇒ new differentiability
f ( x, y ) − f ( x0 , y 0 ) ∂f
x − x0 ∂f
= lim
−
−
( r0 ) rlim
( r0 )
r →r0
→r0 y − y
y − y0
∂x
∂y
1 3
2
1 24 0
4 3
h sinθ
=b / a

17. Old differentiability ⇒ new differentiability
f ( x, y ) − f ( x0 , y 0 ) b ∂f
∂f
= lim
−
( r0 ) − ( r0 )
r →r0
h sinθ
a ∂x
∂y

18. Old differentiability ⇒ new differentiability
=
f ( x0 + bh, y 0 + ah ) − f ( x0 , y 0 ) b ∂f
1
∂f
lim
−
r0 ) −
(
( r0 )
h→0
sinθ 1444444 h
∂y
2444444
3 a ∂x
Duf
u = ( b, a )

19. Old differentiability ⇒ new differentiability
1
b ∂f
∂f
= Duf ( r0 ) −
( r0 ) − ( r0 )
a
a ∂x
∂y
u = ( b, a )

20. Thm: If f is old differentiable at r0
then Duf(r0) exists and:
Duf ( r0 )
∂f
∂f
=
( r0 ) b + ( r0 ) a
∂x
∂y
= ∇f ( r0 ) ×u
• Stewart thm. 11.6.3, Leithold thm. 12.6.2
• u = (b, a)

21. Old differentiability ⇒ new differentiability
f ( x, y ) − f ( x, y 0 ) ∂f
lim
−
( r0 )
r →r0
y − y0
∂y
 b ∂f
1  ∂f
∂f
∂f
= b ( r0 ) + a ( r0 )  −
( r0 ) − ( r0 )
a  ∂x
∂y
∂y
 a ∂x
= 0.

22. Conclusion
• Old differentiability ⇒ new differentiability
⇒ chain rule.

23. Question:
• Old differentiability ⇔ new differentiability?

24. References
• Stewart, Essential Calculus (Thompson, 2007)
• Leithold, The Calculus 7th ed. (Harper, 1996)