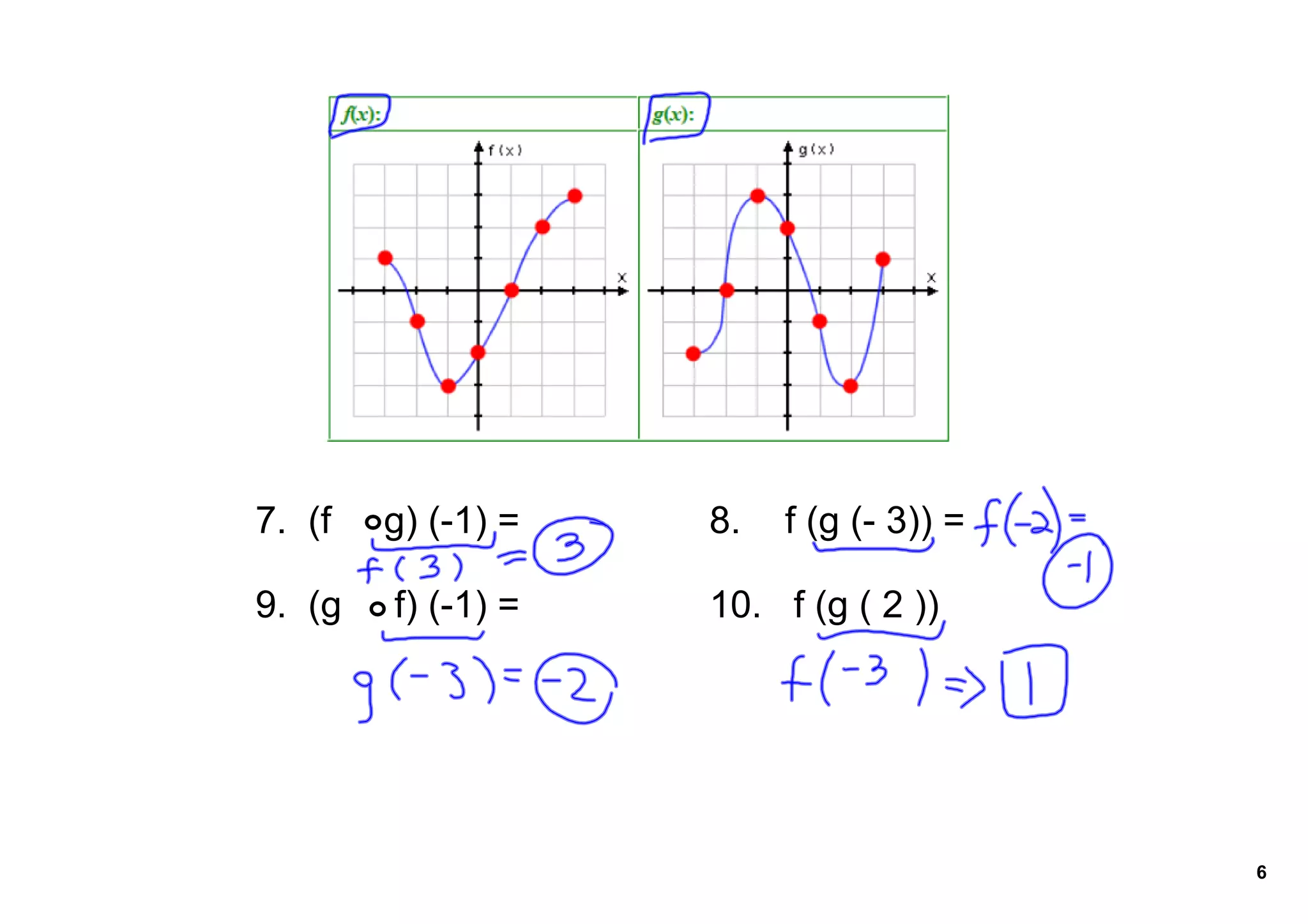
There are several ways to combine two functions, such as addition, subtraction, multiplication, and division of the functions. Another way is function composition, where one function is applied to the output of another function. With composition, the functions are applied from the inside out - first evaluate the inner function, then apply the outer function to the result. Examples show how to evaluate various compositions of the functions f(x) = 2x + 1 and g(x) = x^2.

1. There are several ways in which we can put two functions
together. For example, we could add, subtract, multiply or
divide them...
f(x) + g(x) f(x) ­ g(x) f(x) g(x) f(x) ÷ g(x)
Let f(x) = 2x + 1
g(x) = x2
Find: 1. f(0) + g(­4) 2. f(­3) g(2)
1

2. A composition of functions is another way of "putting" two
functions together...but be careful with notation!!
( f g )(x) is the composition of f and g,
it does not mean to multiply f and g
(f ( g ( x ) ) can also be used as the same notation.
Read as: "f of g of x"
2

3. With compositions work right to left {or inside outside}
(f g)(x) and f(g(x)) (1) Find g(x)
(2) Use this value to find f
(g f)(x) and g(f(x)) (1) Find f(x)
(2) Use this value to find g
3

4. 4

5. Examples: f(x) = 2x + 1 and g(x) = x2
1. (f g)(2) 2. (g f )(2)
3. f (g (3) ) 4. g( f ( 3 ))
5. f(g(f(­2))) 6. g(g(g(2))
5

6. 7. (f g) (­1) = 8. f (g (­ 3)) =
9. (g f) (­1) = 10. f (g ( 2 ))
6