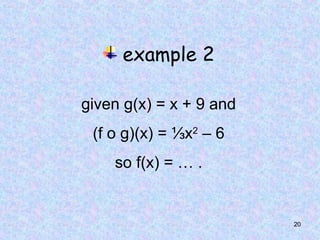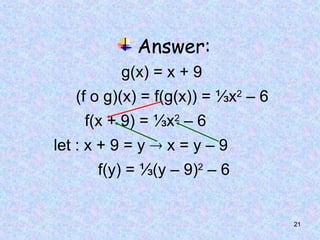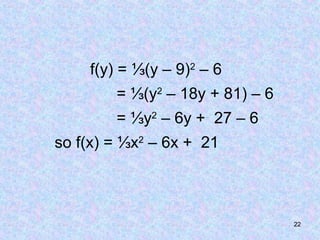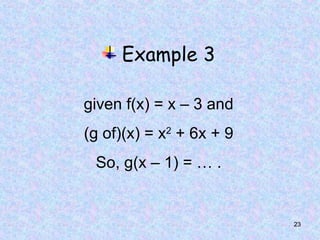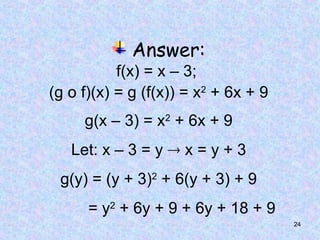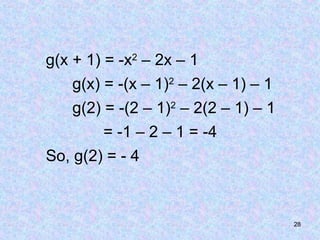The document discusses composite functions, which are created by combining two functions sequentially, resulting in a new function called a composition function. It includes examples, properties such as non-commutativity and associativity, and methods for determining a function when the composition and other functions are known. Additionally, it provides practical examples demonstrating the application of these concepts.

1. 1
Composite
Function

2. 2
Composite Function
Combining the operations of two
functions sequentially will produce
a new function. This combination
is called function composition and
the result is called a composition
function.

3. 3
x  A is mapping f to y  B
write as f : x → y or y = f(x)
y  B is mapping by g to z  C
Write as g : y → z or z = g(y)
or z = g(f(x))
A
x
C
z
B
y
f g

4. 4
then the function that mapping x 
A to z  C
is a composition of functions f and
g
Write as (g o f)(x) = g(f(x))
A B C
x z
y
f g
g o f

5. 5
Example 1
f : A → B and g: B → C
defined as in the picture
determine (g o f)(a) and (g o f)(b)
A B C
a
b
p
q
1
2
3
f g

6. 6
Ans:
A B C
a
b
p
q
1
2
3
f g
f(a) = 1 and g(1) = q
so (g o f)(a) = g(f(a)) = g(1) q
(g o f)(a) = ?

7. 7
A B C
a
b
p
q
1
2
3
f g
f(b) = 3 and g(3) = p
So, (g o f) = g(f(b)) = g(3) = p
(g o f)(b) = ?

8. 8
Peoperties Composite
Function
1.Not commutative :
f o g ≠ g o f
2. Associative :
f o (g o h) = (f o g) o h = f o g o h
3. Has an identity function : I(x) = x
f o I = I o f = f

9. 9
Example 1
f : R → R dan g : R → R
f(x) = 3x – 1 dan g(x) = 2x2
+ 5
Tentukan: a. (g o f)(x)
b. (f o g)(x)

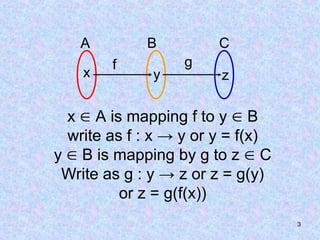
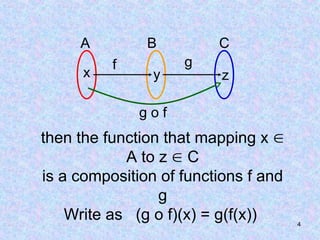
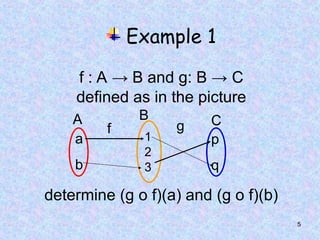
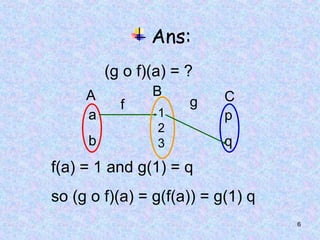
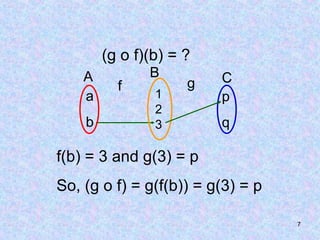
10. 10
Answer:
f(x) = 3x – 1 and g(x) = 2x2
+ 5
a. (g o f)(x) = g[f(x)] = g(3x – 1)
= 2(3x – 1)2
+ 5
= 2(9x2
– 6x + 1) + 5
= 18x2
– 12x + 2 + 5
= 18x2
– 12x + 7

11. 11
f(x) = 3x – 1 and g(x) = 2x2
+ 5
b. (f o g)(x) = f[g(x)] = f(2x2
+ 5)
= 3(2x2
+ 5) – 1
= 6x2
+ 15 – 1
(f o g)(x) = 6x2
+ 14
(g o f)(x) = 18x2
– 12x + 7
(g o f)(x) ≠ (f o g )(x)
not comutative

12. 12

13. 13
Answer:
f(x) = x – 1, g(x) = x2
– 1
and h(x) = 1/x
((f o g) o h)(x) = (f o g)(h(x))
(f o g)(x) = (x2
– 1) – 1
= x2
– 2
(f o g(h(x))) = (f o g)(1/x)
= (1/x)2
– 2

14. 14
f(x) = x – 1, g(x) = x2
– 1
dan h(x) = 1/x
(f o (g o h))(x) = (f(g oh)(x))
(g o h)(x)= g(1/x)
= (1/x)2
– 1
= 1/x2
- 1
f(g o h)(x)= f(1/x2
– 1)
= (1/x2
– 1) – 1
=(1/x)2
– 2

15. 15
Example 3
I(x) = x, f(x) = x2
and g(x) = x + 1
Determine:
a.(f o I)(x) and (g o I)
b.(I o f) and (I o g)

16. 16
Answer:
I(x) = x, f(x) = x2
and g(x) = x + 1
(f o I)(x) = x2
(g o I)(x) = x + 1
(I o f)(x) = x2
(I o g)(x) = x + 1
(I o f)(x) = (f o I) = f

17. 17
Determining a Function If
the Composition Function
and Other Functions Are
Known

18. 18
Example 1
given f(x) = 3x – 1
and (f o g)(x) = x2
+ 5
find g(x).

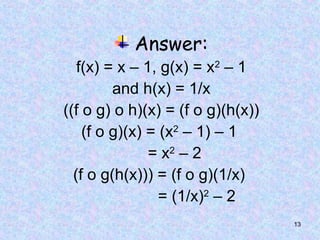
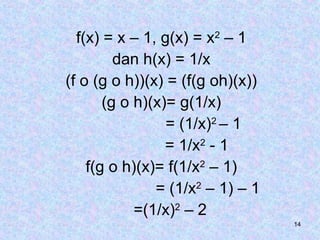
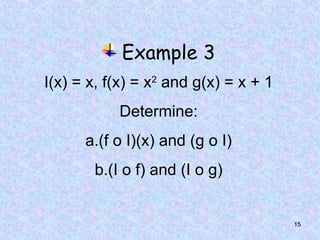
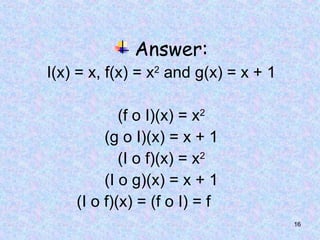
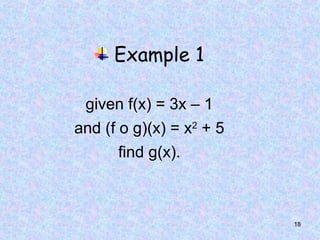
19. 19
answer
f(x) = 3x – 1dan (f o g)(x) = x2
+ 5
fg(x)] = x2
+ 5
3.g(x) – 1 = x2
+ 5
3.g(x) = x2
+ 5 + 1 = x2
+ 6
Jadi g(x) = ⅓(x2
+ 6)

20. 20
example 2
given g(x) = x + 9 and
(f o g)(x) = ⅓x2
– 6
so f(x) = … .

21. 21
Answer:
g(x) = x + 9
(f o g)(x) = f(g(x)) = ⅓x2
– 6
f(x + 9) = ⅓x2
– 6
let : x + 9 = y  x = y – 9
f(y) = ⅓(y – 9)2
– 6

22. 22
f(y) = ⅓(y – 9)2
– 6
= ⅓(y2
– 18y + 81) – 6
= ⅓y2
– 6y + 27 – 6
so f(x) = ⅓x2
– 6x + 21

23. 23
Example 3
given f(x) = x – 3 and
(g of)(x) = x2
+ 6x + 9
So, g(x – 1) = … .

24. 24
Answer:
f(x) = x – 3;
(g o f)(x) = g (f(x)) = x2
+ 6x + 9
g(x – 3) = x2
+ 6x + 9
Let: x – 3 = y  x = y + 3
g(y) = (y + 3)2
+ 6(y + 3) + 9
= y2
+ 6y + 9 + 6y + 18 + 9

25. 25
g(y) = y2
+ 6y + 9 + 6y + 18 + 9
= y2
+ 12y + 36
g(x – 1) = (x – 1)2
+ 12(x – 1) + 36
= x2
– 2x + 1 + 12x – 12 + 36
= x2
+ 10x + 25
So, g(x – 1) = x2
+ 10x + 25

26. 26
Example 4
Given f(x) = 2x + 1
and (f o g)(x + 1)= -2x2
– 4x + 1
Find g(-2) =….

27. 27
Answer:
f(g(x + 1))= -2x2
– 4x + 1
f(x) = 2x + 1 → f(g(x))= 2g(x) + 1
f(g(x + 1)) = 2g (x + 1) + 1
2g(x + 1) + 1 = -2x2
– 4x – 1
2g(x + 1) = -2x2
– 4x – 2
g(x + 1) = -x2
– 2x – 1

28. 28
g(x + 1) = -x2
– 2x – 1
g(x) = -(x – 1)2
– 2(x – 1) – 1
g(2) = -(2 – 1)2
– 2(2 – 1) – 1
= -1 – 2 – 1 = -4
So, g(2) = - 4