1. The document discusses different types of algebraic structures, beginning with groupoids and semigroups. A groupoid is a non-empty set with a binary operation, while a semigroup satisfies the additional property of being associative. 2. Groups are then defined as sets that are closed, associative, have an identity element, and have inverses. Examples of groups include the integers under addition and a set of 3x3 matrices under multiplication. 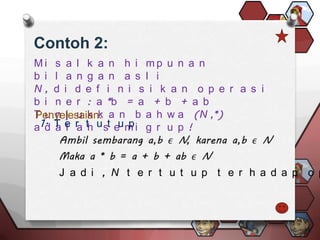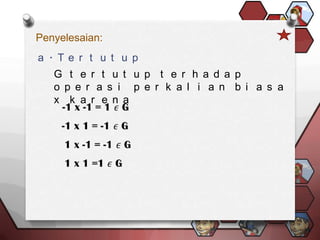3. Abelian groups, also known as commutative groups, are groups where the binary operation is commutative. An example provided is the group of integers under multiplication.

1. STRUKTUR ALJABAR
GRUP
Oleh:
F E L I R A MU R Y
T R I MU H T I H A R Y A N I
Dosen Pengasuh : 1. Dr. Darmawijoyo
2. Dr. Nila Kesumawati, M.Si.

2. O GRUPOID
O SEMIGRUP
O GRUP
O GRUP ABEL

3. GRUPOID
Definisi 1.2.1
Suatu himpunan tidak kosong, G
dengan operasi biner (*) didalamnya,
disebut grupoid dan dinyatakan
dengan (G,*)

4. Contoh 1:
* x y z
x x y y
y y x y
z z y x
Ta be l i ni di ba c a x * x = x , x *
y = y , z * z = x da n s e t e r us ny a
(G ,*) i n i me r u p a k a n
gr up oi d, k a r e na ope r a s i *
me r u pa k a n ope r a s i bi ne r
da l a m G.

5. SEMIGRUP

6. Contoh 2:
Mi s a l k a n h i mp u n a n
b i l a n g a n a s l i
N, d i d e f i n i s i k a n o p e r a s i
b i n e r : a *b = a + b + a b
T u n j u k k a n b a h w a (N ,*)
Penyelesaian:
a 1. T e r th u st eu m i g r u p !
d a l a p
J a d i , N t e r t u t u p t e r h a d a p o p

7. Penyelesaian:
2. A s s o s i a t i f
(a * b ) * c = (a + b + a b ) * c
= (a +b +a b ) + c + (a + b + a b ) c
= a + b + a b + c + a c + b c + a b
a * (b * c ) = a * (b + c + b c )
= a + (b +c +b c ) + a (b + c + b c )
= a + b + c + b c + a b + a c + a b

8. Penyelesaian:
J a d i , (N ,*) m e r u p a k a n s u a t u s e m

9. GRUP
Definisi 1.2.3
Suatu himpunan tidak kosong G
merupakan suatu grup, jika dalam
G terdapat operasi misalkan * dan
unsur-unsur dalam G memenuhi
syarat:

10. Grup
1. T e r t u t u p
2. A s s o s i a t i f

11. Contoh 3:
Penyelesaian:
x -1 1
-1 1 -1
1 -1 1

12. Penyelesaian:
a . Te r t u t u p
G t e r t u t u p t e r h a d a p
o p e r a s i p e r k a l i a n b i a s a
x k a r e n a

13. Penyelesaian:
b . As s o s i a t i f
(a x b) x c = (-1 x -1) x 1 = 1 x 1 = 1
a x (b x c) = -1 x (-1 x 1) = -1 x -1 = 1
s e h i n g g a (a x b ) x c = a
x (b x c ) = 1 m a k a G
a s s o s i a t i f

14. Penyelesaian:
c . A d a n y a e l e m e n i d e n t i t a s (e =
p e r k a l i a n
A mb i l s e mb a r a n g n i l a i d a r i G
-1 x e = e x (-1) = -1
1xe=ex1=1
Ma k a G me mp u n y a i i d e n t i t a s

15. Penyelesaian:
d . Ad a n y a i n v e r s
- A mb i l s e mb a r a n g n i l a i
d a r i G,
- A mb i l s e mb a r a n g n i l a i
d a r i G,
Ma k a a d a i n v e r s u n t u k s e t i a p

16. GRUP ABEL

17. Contoh 4:
Penyelesaian:
-1 x 1 = -1 d a n 1 x (-1) = -1
s e h i n g g a -1 x 1 = 1 x (-1) = -1
J a d i , (G ,x ) m e r u p a k a n g r u p
k o mu t a t i f a t a u g r u p
a b e l .

18. Terima Kasih

19. Elements Page