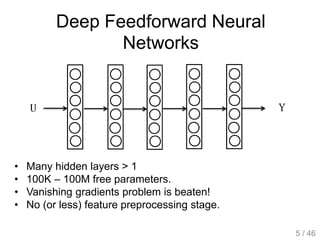
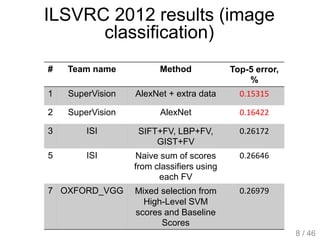
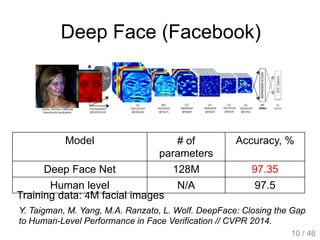
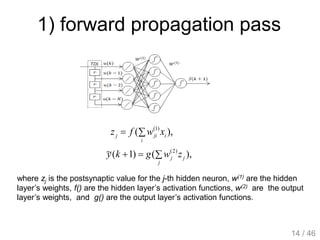
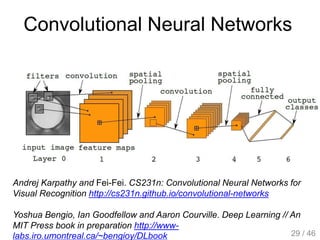
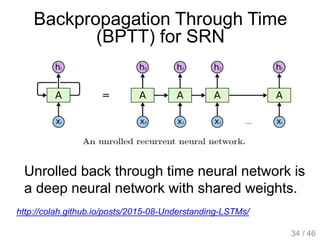
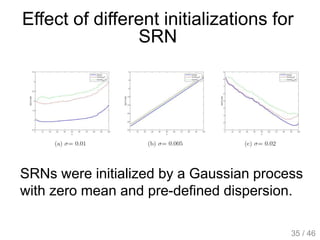
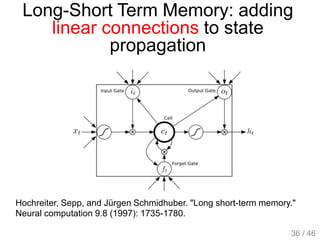
The document provides an overview of deep learning, covering various neural network architectures including deep feedforward neural networks, convolutional neural networks, and recurrent neural networks. It discusses important topics such as the challenges of vanishing gradients, training techniques like backpropagation, and the evolution of models through notable research and datasets like ImageNet. Key advancements in neural network design, performance metrics, and optimization strategies are highlighted throughout the text.

1. Обучение глубоких, очень
глубоких и рекуррентных
сетей
Артем Чернодуб
AI&Big Data Lab, 2 июня 2016, Одесса

2. Neural Network (199x-th)
2 / 46

3. Deep Neural Network (GoogleNet,
2014)
Szegedy, Christian, et al. "Going deeper with convolutions." Proceedings of
the IEEE Conference on Computer Vision and Pattern Recognition, 2015.
3 / 46

4. Classic Feedforward Neural
Networks (before 2006).
• Single hidden layer (Kolmogorov-Cybenko Universal
Approximation Theorem as the main hope).
• Vanishing gradients effect prevents using more layers.
• Less than 10K free parameters.
• Feature preprocessing stage is often critical.
4 / 46

5. Deep Feedforward Neural
Networks
• Many hidden layers > 1
• 100K – 100M free parameters.
• Vanishing gradients problem is beaten!
• No (or less) feature preprocessing stage.
5 / 46

6. Deep Learning = Learning of
Representations (Features)
The traditional model of pattern recognition (since the late
50's):
fixed/engineered features + trainable classifier
Hand-crafted
Feature
Extractor
Trainable
Classifier
Trainable
Feature
Extractor
Trainable
Classifier
End-to-end learning / Feature learning / Deep learning:
trainable features + trainable classifier
6 / 46

7. ImageNet Large Scale Visual
Recognition Challenge (ILSVRC)
Russakovsky, Olga, et al. "Imagenet large scale visual recognition
challenge." International Journal of Computer Vision 115.3 (2015): 211-252.
1000 classes
Train: 1,2M images
Test: 150K images
7 / 46

8. ILSVRC 2012 results (image
classification)
# Team name Method Top-5 error,
%
1 SuperVision AlexNet + extra data 0.15315
2 SuperVision AlexNet 0.16422
3 ISI SIFT+FV, LBP+FV,
GIST+FV
0.26172
5 ISI Naive sum of scores
from classifiers using
each FV
0.26646
7 OXFORD_VGG Mixed selection from
High-Level SVM
scores and Baseline
Scores
0.26979
8 / 46

9. AlexNet, 2012 — MeGa HiT
A. Kryzhevsky, I. Sutskever, G.E. Hinton. ImageNet Classification with
Deep Convolutional Neural Networks // Advances in Neural Information
Processing Systems 25 (NIPS 2012).
9 / 46

10. Deep Face (Facebook)
Y. Taigman, M. Yang, M.A. Ranzato, L. Wolf. DeepFace: Closing the Gap
to Human-Level Performance in Face Verification // CVPR 2014.
Model # of
parameters
Accuracy, %
Deep Face Net 128M 97.35
Human level N/A 97.5
Training data: 4M facial images
10 / 46

11. Deeper, deeper and deeper
Year Net’s name Number of layers Top-5 error,
%
2012 AlexNet 8 15.32
2013 - - -
2014 VGGNet 19 7.10
2015 ResNet 152 4.49
11 / 46

12. Cost of computing
https://en.wikipedia.org/wiki/FLOPS
Year Cost per
GFLOPS in
2013 USD
1997 $42000
2003 $100
2007 $52
2011 $1.80
2013 $0.12
2015 $0.06$
12 / 46

13. Training Neural Networks +
optimization
13 / 46

14. 1) forward propagation pass
),( )1(

i
ijij xwfz
),()1(~ )2(

j
jj zwgky
where zj is the postsynaptic value for the j-th hidden neuron, w(1) are the hidden
layer’s weights, f() are the hidden layer’s activation functions, w(2) are the output
layer’s weights, and g() are the output layer’s activation functions.
14 / 46

15. 2) backpropagation pass
Local gradients calculation:
),1(~)1(  kyktOUT

.)(' )2( OUT
jj
HID
j wzf  
,
)(
)2( j
OUT
j
z
w
kE



.
)(
)1( i
IN
j
ji
x
w
kE



Derivatives calculation:
15 / 46

16. Bad effect of vanishing (exploding)
gradients: two hypotheses
1) increased frequency and
severity of bad local
minima
2) pathological curvature, like
the type seen in the well-
known
Rosenbrock function: 222
)(100)1(),( xyxyxf 
16 / 46

17. Bad effect of vanishing (exploding)
gradients: a problem
,
)( )1()(
)(



 m
i
m
jm
ji
z
w
kE

,' )1()()1()( 
 m
i
i
m
ij
m
j
m
j wf  0
)(
)(



m
jiw
kE
=> 1mfor
17 / 46

18. Backpropagation mechanics in vector
form
)))1(('()()1(  mfdiagmm m aWδδ
Observations:
1mW
1)))1(('( mfdiag a
- robustness (weights decay)
- max(f’) = ¼ for sigmoid
- max(f’) = 1 for tanh
- max(f’) = 1 for ReLU
18 / 46

19. Backpropagation as multiplication of
Jacobians
))).1(('()(  nfdiagn n aWJ
Jacobian of n-th layer:
Local gradients as product of Jacobians:
),1()()()2(  nnnn JJδδ
).1()...1()()()(  hnnnnhn JJJδδ
),()()1( nnn Jδδ 
If ||J(n)|| < 1 – gradient vanishes;
if ||J(n)|| > 1 – gradient probably explodes.
19 / 46

20. Nonlinear Activation functions
Andrej Karpathy and Fei-Fei. CS231n: Convolutional Neural Networks for
Visual Recognition http://cs231n.github.io/convolutional-networks
Yoshua Bengio, Ian Goodfellow and Aaron Courville. Deep Learning // An
MIT Press book in preparation http://www-
labs.iro.umontreal.ca/~bengioy/DLbook
𝑓(𝑥) = max 0, 𝑥
𝑓′
𝑥 =
1, 𝑥 ≥ 0
0, 𝑥 < 0
ReLU activation
function
20 / 46

21. Legendary pretraining
21 / 46

22. Sparse Autoencoders
22 / 46

23. Dimensionality
reduction
• Use a stacked RBM as deep auto-
encoder
1. Train RBM with images as input &
output
2. Limit one layer to few dimensions
 Information has to pass through middle
layer
G. E. Hinton and R. R. Salakhutdinov. Reducing the Dimensionality of Data
with Neural Networks // Science 313 (2006), p. 504 – 507.
23 / 46

24. How to use unsupervised pre-
training stage / 1
24 / 46

25. How to use unsupervised pre-
training stage / 2
25 / 46

26. How to use unsupervised pre-
training stage / 3
26 / 46

27. How to use unsupervised pre-
training stage / 4
27 / 46

28. Why Multilayer Perceptron (it is
a shallow neural network from
1990-th ???
28 / 46

29. Convolutional Neural Networks
Andrej Karpathy and Fei-Fei. CS231n: Convolutional Neural Networks for
Visual Recognition http://cs231n.github.io/convolutional-networks
Yoshua Bengio, Ian Goodfellow and Aaron Courville. Deep Learning // An
MIT Press book in preparation http://www-
labs.iro.umontreal.ca/~bengioy/DLbook 29 / 46

30. Convolution Layer
Andrej Karpathy and Fei-Fei. CS231n: Convolutional Neural Networks for
Visual Recognition http://cs231n.github.io/convolutional-networks
Yoshua Bengio, Ian Goodfellow and Aaron Courville. Deep Learning // An
MIT Press book in preparation http://www-
labs.iro.umontreal.ca/~bengioy/DLbook 30 / 46

31. Implementation tricks: im2col
K. Chellapilla, S. Puri, P. Simard. High Performance Convolutional Neural
Networks for Document Processing // International Workshop on Frontiers
in Handwriting Recognition, 2006.
31 / 46

32. Implementation tricks: im2col for
convolution
K. Chellapilla, S. Puri, P. Simard. High Performance Convolutional Neural
Networks for Document Processing // International Workshop on Frontiers
in Handwriting Recognition, 2006.
32 / 46

33. Recurrent Neural Network
(SRN)
• Pascanu R., Mikolov T., Bengio Y. On the Difficulty of Training Recurrent Neural Networks
// Proc. of “ICML’2013”.
• Q.V. Le, N. Jaitly, G.E. Hinton. “A Simple Way to Initialize Recurrent Networks of Rectified
• Linear Units” (2015)
• M. Ajjovsky, A. Shah, Y. Bengio, "Unitary Evolution Recurrent Neural Networks" (2016)
• Henaff M., Szlam A., LeCun Y. Orthogonal RNNs and Long-Memory Tasks //arXiv preprint
arXiv:1602.06662. – 2016.
33 / 46

34. Backpropagation Through Time
(BPTT) for SRN
http://colah.github.io/posts/2015-08-Understanding-LSTMs/
Unrolled back through time neural network is
a deep neural network with shared weights.
34 / 46

35. Effect of different initializations for
SRN
SRNs were initialized by a Gaussian process
with zero mean and pre-defined dispersion.
35 / 46

36. Long-Short Term Memory: adding
linear connections to state
propagation
Hochreiter, Sepp, and Jürgen Schmidhuber. "Long short-term memory."
Neural computation 9.8 (1997): 1735-1780.
36 / 46

37. Long-Short Term Memory
(LSTM)
http://colah.github.io/posts/2015-08-Understanding-LSTMs/
37 / 46

38. Deep Residual Networks adding
linear connections to the conv nets
He, Kaiming, et al. "Deep Residual Learning for Image Recognition." arXiv
preprint arXiv:1512.03385 (2015).
38 / 46

39. Deep, big, simple neural nets:
no pre-training, simple gradient
descent
Ciresan, Dan Claudiu, et al. "Deep, big, simple neural nets for handwritten
digit recognition." Neural computation 22.12 (2010): 3207-3220.
39 / 46

40. Smart initialization
Glorot, Xavier, and Yoshua Bengio. "Understanding the difficulty of training
deep feedforward neural networks." International conference on artificial
intelligence and statistics. 2010.
40 / 46

41. Batch Normalization: brute force
whitening
Ioffe, Sergey, and Christian Szegedy. "Batch normalization: Accelerating
deep network training by reducing internal covariate shift." arXiv preprint
arXiv:1502.03167 (2015).
41 / 46

42. Orthogonal matrices
Orthogonal matrix is a square matrix with
real entries whose columns and rows are
orthogonal unit vectors, i.e.
IAAAA TT

where I is an identity matrix. Orthogonal
matrix is norm-preserving:
BAB 
where A is orthogonal matrix, B is any
matrix. 42 / 46

43. Examples of orthogonal
matrices
43 / 46

44. Backpropagation mechanics: see again
)))1(('()()1(  mfdiagmm m aWδδ
Linear case – orthogonality of W is enough!
mmm Wδδ )()1( 
Saxe, Andrew M., James L. McClelland, and Surya Ganguli. "Exact
solutions to the nonlinear dynamics of learning in deep linear neural
networks." arXiv preprint arXiv:1312.6120 (2013).
44 / 46

45. Smart orthogonal initialization:
orthogonal + whitening
Mishkin, Dmytro, and Jiri Matas. "All you need is a good init." arXiv preprint
arXiv:1511.06422 (2015).
45 / 46

46. Orthogonal Permutation Linear
Units (OPLU) / sortout
Rennie, Steven J., Vaibhava Goel, and Samuel Thomas. "Deep order
statistic networks." Spoken Language Technology Workshop (SLT), 2014
IEEE. IEEE, 2014.
Chernodub, Artem, and Dimitri Nowicki. "Norm-preserving Orthogonal
Permutation Linear Unit Activation Functions (OPLU)." arXiv preprint
)))1(('()()1(  mfdiagmm m aWδδ
46 / 46

47. contact: a.chernodub@gmail.com
Thanks!