Downloaded 12 times
![Grid Search
1. Define a search space
2. Try all 4*3=12
configurations
Search space for SVM Classifier
{
'C': [1, 10, 100, 1000],
'gamma': [1e-2, 1e-3, 1e-4],
'kernel': ['rbf']
}](https://image.slidesharecdn.com/random-170526111052/85/DataScienceLab2017_-16-320.jpg)
![Random Search
1. Define the search space
2. Sample the search space
and run ML algorithm
Search space for SVM Classifier
{
'C': scipy.stats.expon(scale=100),
'gamma': scipy.stats.expon(scale=.1),
'kernel': ['rbf']
}](https://image.slidesharecdn.com/random-170526111052/85/DataScienceLab2017_-17-320.jpg)
![● X - a search space
{
'C': [1, 1000],
'gamma': [0.0001, 0.1],
'kernel': ['rbf'],
}
Background: Examples](https://image.slidesharecdn.com/random-170526111052/85/DataScienceLab2017_-27-320.jpg)
![experiment = conn.experiments().create(
name='Some Optimization (Python)',
parameters=[
dict(name='C', type='double', bounds=dict(min=0.0, max=1.0)),
dict(name='gamma', type='double', bounds=dict(min=0.0, max=1.0)),
],
)
SigOpt API](https://image.slidesharecdn.com/random-170526111052/85/DataScienceLab2017_-62-320.jpg)
Uploaded byGeeksLab Odessa
DataScienceLab2017_Оптимизация гиперпараметров машинного обучения при помощи Байесовской оптимизации
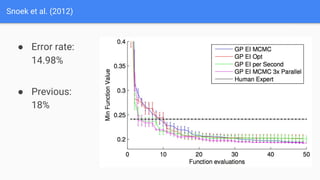
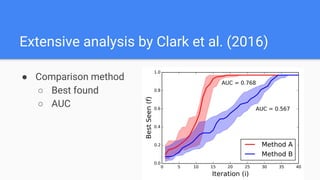
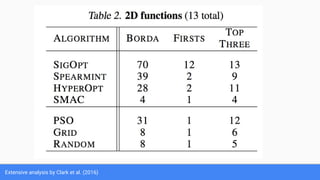
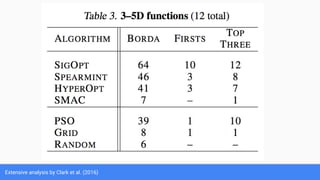
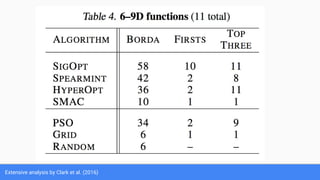
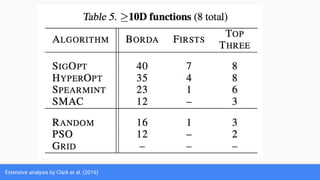
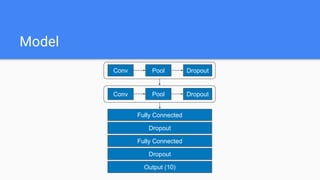
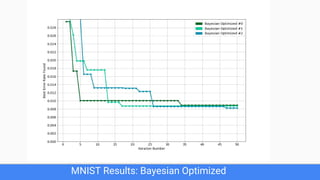
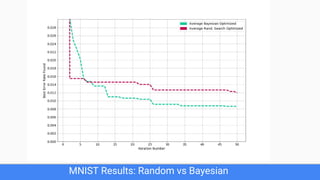
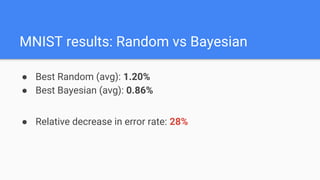
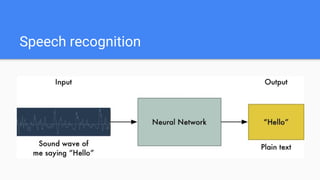
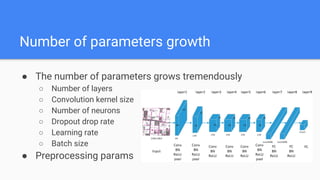
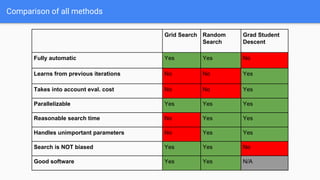
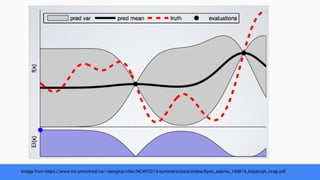
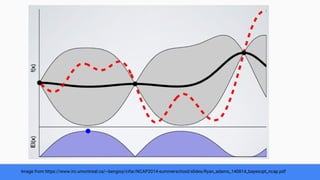
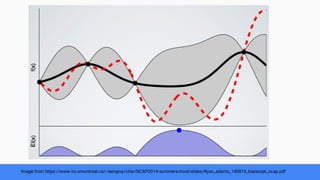
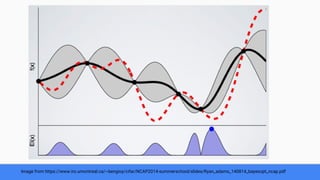
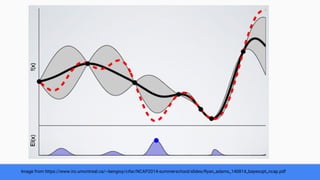
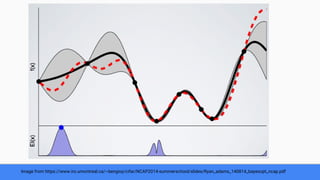
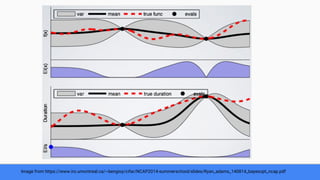
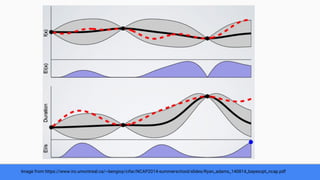
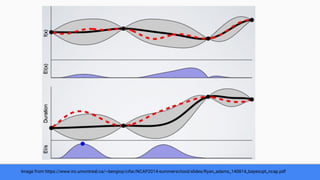
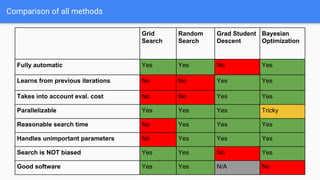
The document discusses Bayesian optimization for tuning machine learning hyper-parameters, highlighting its importance in achieving better algorithm performance. It compares various methodologies such as grid search, random search, and grad student descent, outlining their pros and cons. The author shares personal experiences and research findings to advocate for Bayesian optimization as a preferred method due to its capability of learning from past iterations and considering evaluation costs.
More Related Content
Similar to DataScienceLab2017_Оптимизация гиперпараметров машинного обучения при помощи Байесовской оптимизации
DataScienceLab2017_Оптимизация гиперпараметров машинного обучения при помощи Байесовской оптимизации
- 1. Bayesian Optimization of MLHyper-parameters Maksym Bevza Research Engineer at
- 2. ML solves complexproblems
- 3.
- 4.
- 5.
- 6.
- 7. Other complex problems ●And many more ○ Recommender systems ○ Natural language understanding ○ Robotics ○ Grammatical error correction ○ ...
- 8. Number of parametersgrowth ● The number of parameters grows tremendously ○ Number of layers ○ Convolution kernel size ○ Number of neurons ○ Dropout drop rate ○ Learning rate ○ Batch size ● Preprocessing params
- 9. Tuning parameters ismagic ● Complex systems are hard to analyse ● Impact of parameters on success is obscure
- 10. ● Success ofML algorithm depends on ○ Data ○ Good algorithm/architecture ○ Good parameters settings Tuning parameters is crucial
- 11. ● Success ofML algorithm depends on ○ Data ○ Good algorithm/architecture ○ Good parameters settings Tuning parameters is crucial
- 12. Goals ● Introduce BayesianOptimization to the audience ● Share personal experience ○ Results on digit recognition problem ○ Toolkits for Bayesian Optimization
- 13. Overview ● Tuning MLhyper-parameters ● Bayesian Optimization ● Available software ● Experiments in research field ● My experiments
- 14.
- 15. Tuning ML hyper-parameters ●Grid search ● Random search ● Grad student descent
- 16. Grid Search 1. Definea search space 2. Try all 4*3=12 configurations Search space for SVM Classifier { 'C': [1, 10, 100, 1000], 'gamma': [1e-2, 1e-3, 1e-4], 'kernel': ['rbf'] }
- 17. Random Search 1. Definethe search space 2. Sample the search space and run ML algorithm Search space for SVM Classifier { 'C': scipy.stats.expon(scale=100), 'gamma': scipy.stats.expon(scale=.1), 'kernel': ['rbf'] }
- 18. Grid Search: pros& cons ● Fully automatic ● Parallelizable ● Number experiments grows exponentially with number of params ● Waste of time on unimportant parameters ● Some points in search space are not reachable ● Does not learn from previous iterations
- 19. Random Search: pros& cons ● Fully automatic ● Parallelizable ● Number of iterations are set upfront ● No time waste on unimportant parameters ● All points in the search space are reachable ● Does not learn from previous iterations ● Does not take into account evaluation cost
- 20. ● f(x, y)= g(x) + h(y) ● h(y) is smaller than g(x) Grid Search vs Random Search
- 21. Grad Student Descent ●Researcher fiddles around with the parameters until it works Name of method by Ryan Adams
- 22. Grad Student Descent:pros & cons ● Learns from previous iterations ● Takes into account evaluation cost ● Parallelizable ● Benefits from understanding semantics of hyper-parameters ● Search is biased ● Requires a lot of manual work
- 23. Comparison of allmethods Grid Search Random Search Grad Student Descent Fully automatic Yes Yes No Learns from previous iterations No No Yes Takes into account eval. cost No No Yes Parallelizable Yes Yes Yes Reasonable search time No Yes Yes Handles unimportant parameters No Yes Yes Search is NOT biased Yes Yes No Good software Yes Yes N/A
- 24. Bayesian Optimization: thegoal ● Fully automatic ● Learns from previous iterations ● Takes into account evaluation cost ● Search is not biased ● Parallelizable ● Available software is non-free and not stable
- 25.
- 26. ● Let’s treatour ML learning algorithm as a function f : X -> Y ● X is our search space for hyper-parameters ● Y is set of score that we want to optimize ● Let’s consider other parameters to be fixed (e.g. dataset) Background
- 27. ● X -a search space { 'C': [1, 1000], 'gamma': [0.0001, 0.1], 'kernel': ['rbf'], } Background: Examples
- 28. ● We canoptimize towards any score (even non-differentiable) ○ Validation error rate ○ AUC ○ Recall at fixed FPR ○ Many more Background: Examples
- 29. ● Our MLalgorithm f for similar settings gets similar scores ● We can leverage it to try settings that are more promising ● For custom scores this condition should hold Intuition
- 30. ● Let’s considerone dimensional function f : R -> R ● Let’s suppose we want to minimize f An example Image from https://www.iro.umontreal.ca/~bengioy/cifar/NCAP2014-summerschool/slides/Ryan_adams_140814_bayesopt_ncap.pdf
- 31. ● Build allpossible functions ● Less smooth functions are less probable An example Image from https://www.iro.umontreal.ca/~bengioy/cifar/NCAP2014-summerschool/slides/Ryan_adams_140814_bayesopt_ncap.pdf
- 32.
- 33. Which point totry next?
- 34. ● Exploration: Tryplaces with high variance ● Exploitation: Try places with low mean Exploration / Exploitation tradeoff
- 35. ● Probability ofImprovement (PI) ● Expected Improvement (EI) ● Other complicated ones Strategies of choosing next point
- 36.
- 37. Let’s go stepby step
- 38.
- 39.
- 40.
- 41.
- 42.
- 43.
- 44.
- 45. What about costof evaluation?
- 46. ● Hyper-parameters oftenimpact the evaluation time ● Number of hidden layers, neurons per layer (Deep Learning) ● Number and depth of trees (Random Forest) ● Number of estimators (Gradient Boosting) Time limits vs evaluation limits
- 47. ● In practicewe deal with time limits ● E.g. what’s the best set-up we can get in 7 days? ● Try cheap evaluations first ● Given rough characteristic of f, try expensive evaluations Time limits vs evaluation limits
- 48. How to accountfor cost of evaluation?
- 49. ● Let’s estimatetwo functions at a time: ○ The function f itself ○ The cost of evaluation (duration) of function f ● We can use BO to estimate those functions How to account for cost of evaluation?
- 50. ● We chosedthe point with highest Expected Improvement ● Pick the highest EI/second instead Strategy of choosing next point with cost
- 51.
- 52.
- 53.
- 54. Comparison of allmethods Grid Search Random Search Grad Student Descent Bayesian Optimization Fully automatic Yes Yes No Yes Learns from previous iterations No No Yes Yes Takes into account eval. cost No No Yes Yes Parallelizable Yes Yes Yes Tricky Reasonable search time No Yes Yes Yes Handles unimportant parameters No Yes Yes Yes Search is NOT biased Yes Yes No Yes Good software Yes Yes N/A No
- 55.
- 56. ● Bayesian optimizationsoftware is tricky to build ● Leveraging clusters for parallelization is hard ● No hype around it What’s the catch?
- 57.
- 58. ● The toolkitsbuilt by researchers are not supported well ○ Spearmint ○ SMAC ○ HyperOpt ○ BayesOpt ● Non-bayesian alternatives ○ TPE (Tree-structured Parzen Estimator) ○ PSO (Particle Swarm Optimization) Available software
- 59. ● SigOpt providesBayesian Optimization as a service ● Claims state-of-the-art Bayesian Optimization ● Their customers ○ Prudential ○ Huawei ○ MIT ○ Hotwire ○ ... SigOpt
- 60.
- 61. from sigopt importConnection conn = Connection(client_token='TOKEN') SigOpt API
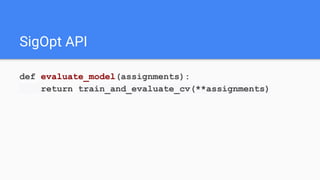
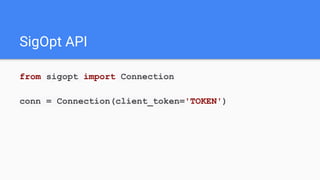
- 62. experiment = conn.experiments().create( name='SomeOptimization (Python)', parameters=[ dict(name='C', type='double', bounds=dict(min=0.0, max=1.0)), dict(name='gamma', type='double', bounds=dict(min=0.0, max=1.0)), ], ) SigOpt API
- 63. for _ inrange(30): suggestion = conn.experiments(experiment.id).suggestions().create() value = evaluate_model(suggestion.assignments) conn.experiments(experiment.id).observations().create( suggestion=suggestion.id, value=value, ) SigOpt API
- 64.
- 65. Snoek et al.(2012) ● CIFAR-10 ○ 60000 images ○ 32x32 colour ○ 10 classes ● Error rate: 14.98% ○ New state-of-the-art result (in 2012)
- 66. Snoek et al.(2012) ● Error rate: 14.98% ● Previous: 18%
- 67. Extensive analysis byClark et al. (2016) ● Extensive analysis of BO and other search methods ● Different type of functions ○ Oscillatory ○ Discrete values ○ Boring ○ ...
- 68. Extensive analysis byClark et al. (2016) ● Comparison method ○ Best found ○ AUC
- 69. Extensive analysis byClark et al. (2016) ● For each function ○ First placed ○ Top three ○ Borda
- 70. Extensive analysis byClark et al. (2016)
- 71. Extensive analysis byClark et al. (2016)
- 72. Extensive analysis byClark et al. (2016)
- 73. Extensive analysis byClark et al. (2016)
- 74.
- 75. Task ● Digit recognition ●MNIST dataset ○ 70000 images ○ 28x28 grayscale ○ 10 classes
- 76. Model Conv Pool Dropout FullyConnected Fully Connected Output (10) Dropout Dropout Conv Pool Dropout
- 77. ● 6 parameterstuned ○ Number of filters per layer (1) ○ Number of convolution layers (1) ○ Dense layers size (2) ○ Batch size (1) ○ Learning rate (1) Parameters of the model
- 78. ● Features ○ Parametertypes: INT, FLOAT, ENUM ○ Evaluation data stored in MongoDB ○ Works with noisy functions ● License: Non-commercial usage Spearmint
- 79.
- 80. MNIST Results: RandomSearch
- 81. MNIST Results: BayesianOptimized
- 82. MNIST Results: Randomvs Bayesian
- 83. ● Best Random(avg): 1.20% ● Best Bayesian (avg): 0.86% ● Relative decrease in error rate: 28% MNIST results: Random vs Bayesian
- 84.
- 85. ● Spearmint triesboundaries first ○ Be cautious in setting up your search space ● Use logarithmic scales when it makes sense ● Recommendations on iteration limit ○ 10-20 iterations per one parameter Gotchas
- 86. Conclusions ● Bayesian Optimizationleads to better results ● SigOpt is hopefully first stable implementation of BO
- 87. Thanks! Maksym Bevza Research Engineerat Grammarly maksym.bevza@grammarly.com www.grammarly.com