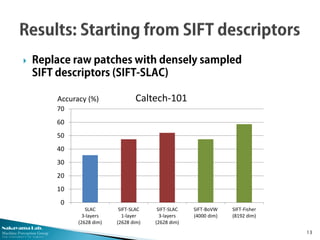
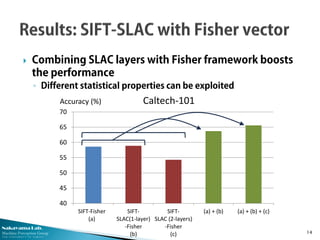
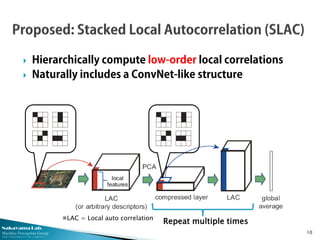
This document describes research from the Nakayama Lab at the University of Tokyo on deep learning approaches for computer vision tasks. It discusses stacked local autocorrelation (SLAC) features, which involve iteratively computing local autocorrelations and compressing with PCA. The SLAC approach achieves better performance than standard higher-order local autocorrelation features while using lower-dimensional representations. Combining SLAC with other frameworks like Fisher vectors can further boost performance on datasets like Caltech-101. Overall, the document advocates for deep learning by stacking different single-layer modules as a simple but powerful framework.

1. Nakayama Lab.
Machine Perception Group
The University of Tokyo
The University of Tokyo
Grad. School of Information Science and Technology
Hideki Nakayama

2. Nakayama Lab.
Machine Perception Group
The University of Tokyo
 Deep learning
◦ Successive local response filters and pooling layers
◦ State-of-the-art performance on many tasks & benchmarks
 Traditional BoW-based models are often referred to as
“shallow learning” (interpreted as a single-layer network)
2
[A. Krizhevsky et al., NIPS’12]

3. Nakayama Lab.
Machine Perception Group
The University of Tokyo
To achieve a certain level of representational power...
 Deep models are believed to require fewer free parameters
or neurons [Larochelle et al., 2007] [Bengio, 2009] [Delalleau and Bengio, 2011]
(not fully proved except for some specific cases, though.)
 However, optimization of deep models is challenging
◦ Non-convex, local minima, many heuristic hyperparameters...
◦ Optimizing shallow network is relatively easy (convex in many cases)
3
(If successfully
trained)  Better generalization
 Computational efficiency
 Scalability
Objection:
“Do Deep Nets Really
Need to be Deep?”
[Ba & Caruana, 2014]

4. Nakayama Lab.
Machine Perception Group
The University of Tokyo
 Suboptimal (layer-wise)
 Reasonable performance
◦ Even random weights
could work! [Jarrette, 2009]
 Easiness in tuning
 Stability in learning
 Flexibility in the choice of
layer modules
 Global optimality through
the entire network
 State-of-the-art performance
 Difficulty in optimization
 Computational cost
 Constraints on layer modules
4
Fine-tuning (back propagation)
through the entire network is
the key to the best performance!
Structure of the deep network
itself has the primary importance!
Global training of deep models Stacking single-layer
learning modules
◎
◎△
○

5. Nakayama Lab.
Machine Perception Group
The University of Tokyo
 Suboptimal (layer-wise)
 Reasonable performance
◦ Even random weights
could work! [Jarrette, 2009]
 Easiness in tuning
 Stability in learning
 Flexibility in the choice of
layer modules
 Global optimality through
the entire network
 State-of-the-art performance
 Difficulty in optimization
 Computational cost
 Constraints on layer modules
5
Fine-tuning (back propagation)
through the entire network is
the key to the best performance!
Structure of the deep network
itself has the primary importance!
Global training of deep models Stacking single-layer
learning modules
◎
◎△
○

6. Nakayama Lab.
Machine Perception Group
The University of Tokyo
Empirically studied on top of the bag-of-words framework
 Hyperfeatures [Agarwal et al., ECCV’06]
◦ Hierarchically stack bag-of-visual-words layers
 Deep Fisher Network [Simonyan et al., NIPS’13]
 Deep Sparse Coding [He et al., SDM’14]
6

7. Nakayama Lab.
Machine Perception Group
The University of Tokyo
 Higher-order Local Auto-Correlation (HLAC) features
◦ Non-linear filter (mask) response + average pooling
◦ Successfully deployed in many visual recognition applications
 Cons:
◦ Higher-order correlation & masks are required to achieve good
performance, making the feature representation high-dimensional
7

8. Nakayama Lab.
Machine Perception Group
The University of Tokyo
 Sum-product network [Poon and Domingos, UAI’11]
◦ A deep network where each node (neuron) outputs the sum or
product of input variables
 To represent the same functions, the number of nodes
has to grow: [Delalleau & Bengio, NIPS’11]
◦ Exponentially in a shallow network
◦ Linearly in a deep network
8

9. Nakayama Lab.
Machine Perception Group
The University of Tokyo
 So, why not use deep models?
9

10. Nakayama Lab.
Machine Perception Group
The University of Tokyo
 Hierarchically compute low-order local correlations
 Naturally includes a ConvNet-like structure
10
※LAC = Local auto correlation
Repeat multiple times

11. Nakayama Lab.
Machine Perception Group
The University of Tokyo
 Datasets
◦ MNIST [LeCun,1999]
 Digit recognition
 60k training/10k testing samples
 28x28 pixels
◦ CIFAR-10 [Krizhevsky, 2009]
 Object recognition
 50k training/10k testing samples
 32x32 pixels
◦ Caltech-101 [Fei-Fei, 2004]
 Object recognition
 30 training/15 testing samples
(per class)
 Classifier
◦ Logistic regression
11

12. Nakayama Lab.
Machine Perception Group
The University of Tokyo
 SLAC achieves better performance than standard
HLAC with reduced feature dimensions
12
84
86
88
90
92
94
96
98
100
HLAC
2nd-order
(35 dim)
HLAC
2nd-order
mask size 5
(219 dim)
HLAC
3rd-order
(153 dim)
HLAC
3rd-order
(2245 dim)
SLAC
2-layers
(1176 dim)
0
10
20
30
40
50
60
70
HLAC
1st-order
(45 dim)
HLAC
2nd-order
(739 dim)
HLAC
2nd-order
mask size 5
(5419 dim)
HLAC
3rd-order
(8023 dim)
SLAC
2-layers
(1176 dim)
Accuracy (%) Accuracy (%)MNIST (gray scale) CIFAR-10 (color)

13. Nakayama Lab.
Machine Perception Group
The University of Tokyo
 Replace raw patches with densely sampled
SIFT descriptors (SIFT-SLAC)
13
0
10
20
30
40
50
60
70
SLAC
3-layers
(2628 dim)
SIFT-SLAC
1-layer
(2628 dim)
SIFT-SLAC
3-layers
(2628 dim)
SIFT-BoVW
(4000 dim)
SIFT-Fisher
(8192 dim)
Accuracy (%) Caltech-101

14. Nakayama Lab.
Machine Perception Group
The University of Tokyo
 Combining SLAC layers with Fisher framework boosts
the performance
◦ Different statistical properties can be exploited
14
40
45
50
55
60
65
70
SIFT-Fisher
(a)
SIFT-
SLAC(1-layer)
-Fisher
(b)
SIFT-
SLAC (2-layers)
-Fisher
(c)
(a) + (b) (a) + (b) + (c)
Accuracy (%) Caltech-101

15. Nakayama Lab.
Machine Perception Group
The University of Tokyo
 Deep learning by stacking is a simple but powerful, flexible
framework to integrate various single-layer modules
 Stacked local autocorrelation (SLAC) features
◦ Iterate computation of local autocorrelation and PCA compression
◦ More efficient than standard HLAC that computes everything in a
single layer
◦ Using multiple layers makes sense
 Learning polynomials is a hot topic in ML
◦ R. Livni et al., Vanishing Component Analysis, In Proc. ICML, 2013.
◦ A. Andoni et al., Learning Polynomials with Neural Networks, In Proc. ICML, 2014.
15