Chitta Ranjan, profile picture
Uploaded byChitta Ranjan
PDF, PPTX190 views

Evolution of Deep Learning and new advancements

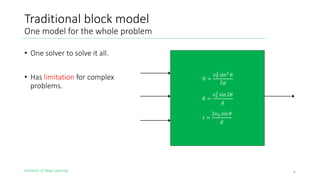
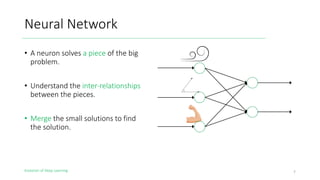
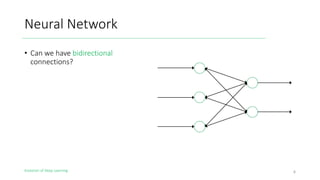
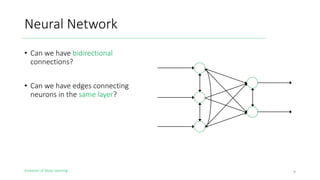
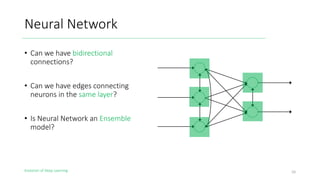
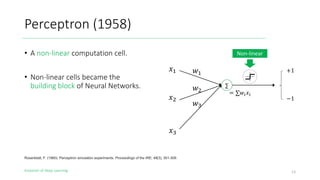
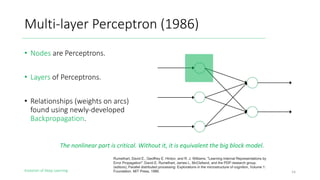
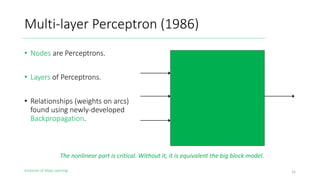
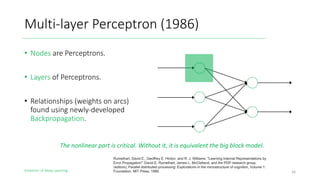
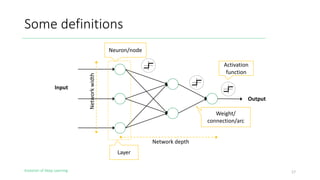
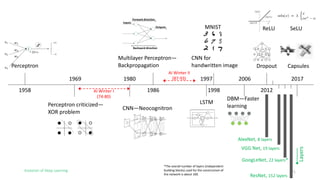
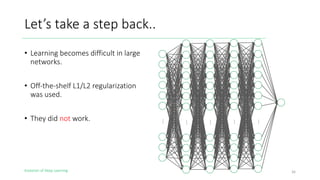
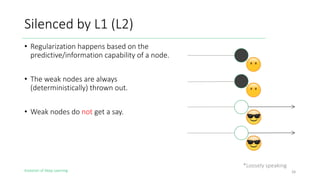
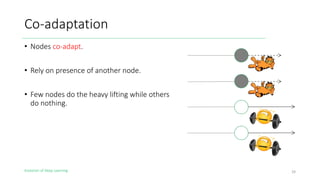
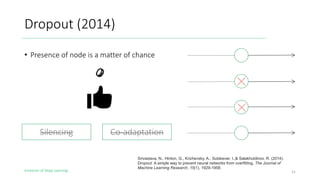
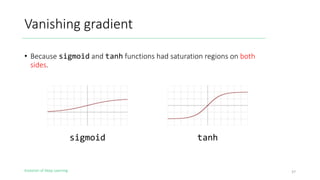
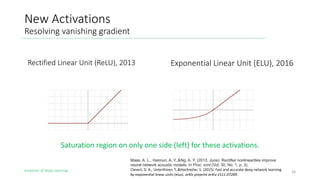
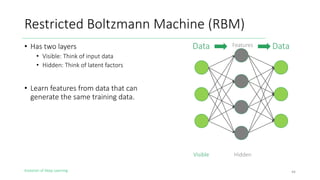
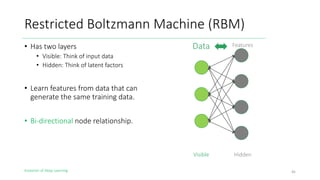
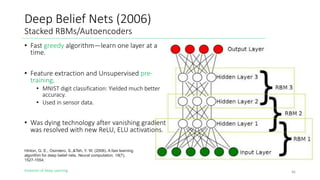
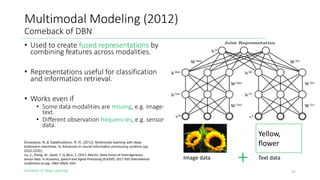
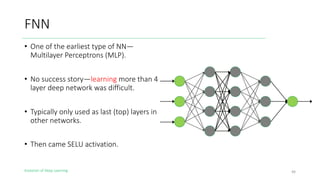
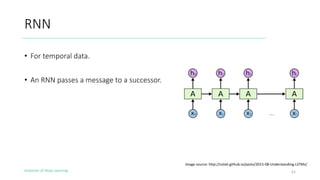
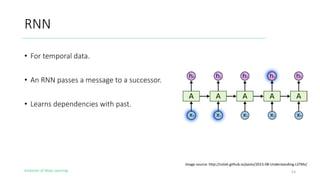
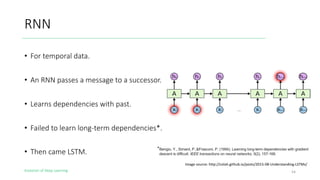
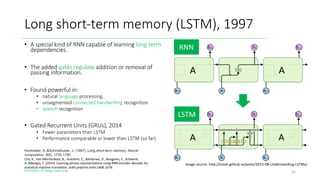
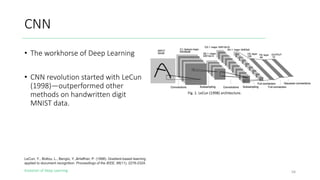
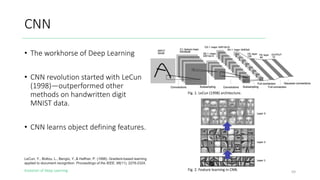
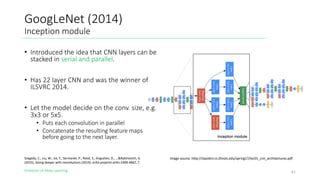
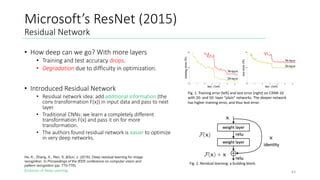
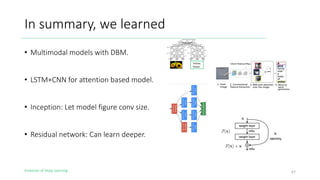
The document outlines the evolution of deep learning, discussing neural networks, their development, and various advancements such as multi-layer perceptrons and dropout techniques. It highlights key challenges in deep learning, like overfitting and the vanishing gradient problem, and presents solutions such as new activation functions and model types including convolutional and recurrent neural networks. Additionally, it situates important historical milestones in deep learning from the perceptron model to complex architectures like LSTM and attention-based models.

Technology◦
Related topics:
Deep Learning•

Embed presentation

Download as PDF, PPTX
Evolution of Deep Learning: New Methods and Applications Chitta Ranjan, Ph.D. Pandora Media. Feb 15, 2018 nk.chitta.ranjan@gmail.com 1
Evolution of Deep Learning Outline • Background • Challenges • Solutions 2
Evolution of Deep Learning How does our brain work? • How do we know where the ball will fall? 3
Evolution of Deep Learning How does our brain work? • How do we know where the ball will fall? • Do we solve these equations in our head? No. 4 ! = #$ % sin% ) 2+ , = #$ % sin 2) + - = 2#$ sin ) +
Evolution of Deep Learning How does our brain work? • How do we know where the ball will fall? • Do we solve these equations in our head? No. • Perhaps we break the problem into pieces and solve it. 5
Evolution of Deep Learning Traditional block model One model for the whole problem 6 • One solver to solve it all. • Has limitation for complex problems. ! = #$ % sin% ) 2+ , = #$ % sin 2) + - = 2#$ sin ) +
Evolution of Deep Learning Neural Network 7 • A neuron solves a piece of the big problem. • Understand the inter-relationships between the pieces. • Merge the small solutions to find the solution.
Evolution of Deep Learning Neural Network 8 • Can we have bidirectional connections?
Evolution of Deep Learning Neural Network 9 • Can we have bidirectional connections? • Can we have edges connecting neurons in the same layer?
Evolution of Deep Learning Neural Network 10 • Can we have bidirectional connections? • Can we have edges connecting neurons in the same layer? • Is Neural Network an Ensemble model?
Evolution of Deep Learning Birth of Neural Network 11
Evolution of Deep Learning Perceptron (1958) 12 Rosenblatt, F. (1960). Perceptron simulation experiments. Proceedings of the IRE, 48(3), 301-309.
Evolution of Deep Learning Perceptron (1958) ∑ !" !# !$ %" %# %$ = ∑%(!( +1 −1 Non-linear 13 • A non-linear computation cell. • Non-linear cells became the building block of Neural Networks. Rosenblatt, F. (1960). Perceptron simulation experiments. Proceedings of the IRE, 48(3), 301-309.
Evolution of Deep Learning Multi-layer Perceptron (1986) 14 • Nodes are Perceptrons. • Layers of Perceptrons. • Relationships (weights on arcs) found using newly-developed Backpropagation. The nonlinear part is critical. Without it, it is equivalent the big block model. Rumelhart, David E., Geoffrey E. Hinton, and R. J. Williams. "Learning Internal Representations by Error Propagation". David E. Rumelhart, James L. McClelland, and the PDP research group. (editors), Parallel distributed processing: Explorations in the microstructure of cognition, Volume 1: Foundation. MIT Press, 1986.
Evolution of Deep Learning Multi-layer Perceptron (1986) 15 • Nodes are Perceptrons. • Layers of Perceptrons. • Relationships (weights on arcs) found using newly-developed Backpropagation. The nonlinear part is critical. Without it, it is equivalent the big block model.
Evolution of Deep Learning Multi-layer Perceptron (1986) 16 • Nodes are Perceptrons. • Layers of Perceptrons. • Relationships (weights on arcs) found using newly-developed Backpropagation. The nonlinear part is critical. Without it, it is equivalent the big block model. Rumelhart, David E., Geoffrey E. Hinton, and R. J. Williams. "Learning Internal Representations by Error Propagation". David E. Rumelhart, James L. McClelland, and the PDP research group. (editors), Parallel distributed processing: Explorations in the microstructure of cognition, Volume 1: Foundation. MIT Press, 1986.
Evolution of Deep Learning Some definitions 17 Activation function Neuron/node Layer Network depth Networkwidth Weight/ connection/arc Input Output
Evolution of Deep Learning We learned.. 18
Evolution of Deep Learning So far we learned • Problem to be broken into pieces (at nodes). • Non-linear decision makers. 19
Evolution of Deep Learning Timeline 20
Evolution of Deep Learning 1980 Capsules SeLU 2017 Dropout 2012 ReLU ResNet, 152 layers GoogLeNet, 22 layers* VGG Net, 19 layers AlexNet, 8 layers Layers Perceptron 1958 1969 Perceptron criticized— XOR problem ∑ !" !# !$ %" %# %$ = ∑%(!( +1 −1 1987 1986 Multilayer Perceptron— Backpropagation Inputs Outputs Forward direction Backward direction AI Winter I (74-80) 2006 CNN for handwritten image 1998 CNN—Neocognitron AI Winter II (87-93) 1997 LSTM DBM—Faster learning *The overall number of layers (independent building blocks) used for the construction of the network is about 100. 21 MNIST
Evolution of Deep Learning Challenges Computation GPU! 22
Evolution of Deep Learning Challenges Computation GPU! 23
Evolution of Deep Learning Challenges Estimation Overfitting Vanishing gradient Dropout Activation functions 24
Evolution of Deep Learning Dropout 25
Evolution of Deep Learning Let’s take a step back.. 26 ⋮ ⋮ ⋮ ⋮ ⋮ • Learning becomes difficult in large networks. • Off-the-shelf L1/L2 regularization was used. • They did not work.
Evolution of Deep Learning Silenced by L1 (L2) • Regularization happens based on the predictive/information capability of a node. 27
Evolution of Deep Learning Silenced by L1 (L2) • Regularization happens based on the predictive/information capability of a node. • The weak nodes are always (deterministically) thrown out. • Weak nodes do not get a say. 28 *Loosely speaking
Evolution of Deep Learning Co-adaptation • Nodes co-adapt. • Rely on presence of another node. • Few nodes do the heavy lifting while others do nothing. 29
Evolution of Deep Learning 30 Wide networks doesn’t really help.
Evolution of Deep Learning Dropout (2014) • Presence of node is a matter of chance 31 Silencing Co-adaptation Srivastava, N., Hinton, G., Krizhevsky, A., Sutskever, I.,& Salakhutdinov, R. (2014). Dropout: A simple way to prevent neural networks from overfitting. The Journal of Machine Learning Research, 15(1), 1929-1958.
Evolution of Deep Learning Dropout with Gaussian gate (2017) • Regular dropout: multiply activations with Bernoulli RVs. • Generalization: Multiply with any RV. 32 !" !# !$ !% ~'(!)(+) ~'(!)(+) ~'(!)(+) ~'(!)(+) Molchanov, D., Ashukha, A.,&Vetrov, D. (2017). Variational dropout sparsifies deep neural networks. arXiv preprint arXiv:1701.05369.
Evolution of Deep Learning Dropout with Gaussian gate (2017) • Regular dropout: multiply activations with Bernoulli RVs. • Generalization: Multiply with any RV. • Gaussian gates is found to improve dropout’s performance. 33 !" !# !$ !% ~'(!)(+) ~'(!)(+) ~'(!)(+) ~'(!)(+) ~-(0,1) ~-(0,1) ~-(0,1) ~-(0,1) Molchanov, D., Ashukha, A.,&Vetrov, D. (2017). Variational dropout sparsifies deep neural networks. arXiv preprint arXiv:1701.05369.
Evolution of Deep Learning Activation functions 34
Evolution of Deep Learning Vanishing Gradient in Deep Networks 35 ⋮ ⋮ ⋮ ⋮ ⋮ """" • Learning was still difficult in large networks. • Activation functions at the time caused the gradient to vanish in lower layers. • Difficult to learn weights. Backpropagation
Evolution of Deep Learning 36 Deep networks doesn’t really help.
Evolution of Deep Learning Vanishing gradient • Because sigmoid and tanh functions had saturation regions on both sides. 37 sigmoid tanh
Evolution of Deep Learning New Activations Resolving vanishing gradient Rectified Linear Unit (ReLU), 2013 38 Maas, A. L., Hannun, A. Y.,&Ng, A. Y. (2013, June). Rectifier nonlinearities improve neural network acoustic models. In Proc. icml (Vol. 30, No. 1, p. 3). Clevert, D. A., Unterthiner, T.,&Hochreiter, S. (2015). Fast and accurate deep network learning by exponential linear units (elus). arXiv preprint arXiv:1511.07289. Exponential Linear Unit (ELU), 2016 Saturation region on only one side (left) for these activations.
Evolution of Deep Learning We learned.. 39
Evolution of Deep Learning So far we learned • Problem to be broken into pieces (at nodes). • Non-linear decision makers. • Challenges met • Overfitting: Dropout • Vanishing gradient: New activations 40
Evolution of Deep Learning Model types 41
Evolution of Deep Learning Types of Models • Unsupervised • Deep Belief Networks (DBN) • Supervised • Feed-forward Neural Network (FNN) • Recurrent Neural Network (RNN) • Convolutional Neural Network (CNN) 42
Evolution of Deep Learning Deep Belief Networks (DBN) 43
Evolution of Deep Learning Restricted Boltzmann Machine (RBM) • Has two layers • Visible: Think of input data • Hidden: Think of latent factors • Learn features from data that can generate the same training data. 44 HiddenVisible FeaturesData Data
Evolution of Deep Learning Restricted Boltzmann Machine (RBM) • Has two layers • Visible: Think of input data • Hidden: Think of latent factors • Learn features from data that can generate the same training data. • Bi-directional node relationship. 45 HiddenVisible FeaturesData
Evolution of Deep Learning Deep Belief Nets (2006) Stacked RBMs/Autoencoders 46 • Fast greedy algorithm—learn one layer at a time. • Feature extraction and Unsupervised pre- training. • MNIST digit classification: Yielded much better accuracy. • Used in sensor data. • Was dying technology after vanishing gradient was resolved with new ReLU, ELU activations. Hinton, G. E., Osindero, S.,&Teh, Y. W. (2006). A fast learning algorithm for deep belief nets. Neural computation, 18(7), 1527-1554.
Evolution of Deep Learning Multimodal Modeling (2012) Comeback of DBN Image data Text data 47 Yellow, flower + • Used to create fused representations by combining features across modalities. • Representations useful for classification and information retrieval. • Works even if • Some data modalities are missing, e.g. image- text. • Different observation frequencies, e.g. sensor data. Srivastava, N.,& Salakhutdinov, R. R. (2012). Multimodal learning with deep boltzmann machines. In Advances in neural information processing systems (pp. 2222-2230). Liu, Z., Zhang, W., Quek, T. Q.,&Lin, S. (2017, March). Deep fusion of heterogeneous sensor data. In Acoustics, Speech and Signal Processing (ICASSP), 2017 IEEE International Conference on (pp. 5965-5969). IEEE.
Evolution of Deep Learning Feed-forward Neural Network (FNN) 48
Evolution of Deep Learning FNN 49 • One of the earliest type of NN— Multilayer Perceptrons (MLP). • No success story—learning more than 4 layer deep network was difficult. • Typically only used as last (top) layers in other networks. • Then came SELU activation.
Evolution of Deep Learning Scaled Exponential Linear Units (SELU), 2017 Self-normalizing Neural Networks. New life for FNNs. 50 Klambauer, G., Unterthiner, T., Mayr, A.,&Hochreiter, S. (2017). Self-normalizing neural networks. In Advances in Neural Information Processing Systems (pp. 972-981). • Activations automatically converge to zero mean and unit variance. • Converges in presence of noise and perturbations. • Allows • train deep networks with many layers, • employ strong regularization schemes, and • to make learning highly robust.
Evolution of Deep Learning Recurrent Neural Network (RNN) 51
Evolution of Deep Learning RNN Image source: http://colah.github.io/posts/2015-08-Understanding-LSTMs/ 52 • For temporal data. • An RNN passes a message to a successor.
Evolution of Deep Learning RNN Image source: http://colah.github.io/posts/2015-08-Understanding-LSTMs/ 53 • For temporal data. • An RNN passes a message to a successor. • Learns dependencies with past.
Evolution of Deep Learning RNN Image source: http://colah.github.io/posts/2015-08-Understanding-LSTMs/ 54 *Bengio, Y., Simard, P.,&Frasconi, P. (1994). Learning long-term dependencies with gradient descent is difficult. IEEE transactions on neural networks, 5(2), 157-166. • For temporal data. • An RNN passes a message to a successor. • Learns dependencies with past. • Failed to learn long-term dependencies*. • Then came LSTM.
Evolution of Deep Learning Long short-term memory (LSTM), 1997 55 Image source: http://colah.github.io/posts/2015-08-Understanding-LSTMs/ RNN LSTM Hochreiter, S.,&Schmidhuber, J. (1997). Long short-term memory. Neural computation, 9(8), 1735-1780. Cho, K., Van Merriënboer, B., Gulcehre, C., Bahdanau, D., Bougares, F., Schwenk, H.,&Bengio, Y. (2014). Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv preprint arXiv:1406.1078. • A special kind of RNN capable of learning long-term dependencies. • The added gates regulate addition or removal of passing information. • Found powerful in: • natural language processing, • unsegmented connected handwriting recognition • speech recognition • Gated Recurrent Units (GRUs), 2014 • Fewer parameters than LSTM. • Performance comparable or lower than LSTM (so far).
Evolution of Deep Learning Attention Based Model (2015) • CNN together with LSTM. • Automatically learns • to fix gaze on salient objects. • Object alignments. • Object relationships with sequence of words. 56 Xu, K., Ba, J., Kiros, R., Cho, K., Courville, A., Salakhudinov, R., ...&Bengio, Y. (2015, June). Show, attend and tell: Neural image caption generation with visual attention. In International Conference on Machine Learning (pp. 2048-2057). Fig. 1. Attention model architecture. Fig. 2. Examples of attending to the correct object (white indicates the attended regions, underlines indicated the corresponding word).
Evolution of Deep Learning Convolutional Neural Network (CNN) 57
Evolution of Deep Learning CNN • The workhorse of Deep Learning • CNN revolution started with LeCun (1998)—outperformed other methods on handwritten digit MNIST data. 58 LeCun, Y., Bottou, L., Bengio, Y.,&Haffner, P. (1998). Gradient-based learning applied to document recognition. Proceedings of the IEEE, 86(11), 2278-2324. Fig. 1. LeCun (1998) architecture.
Evolution of Deep Learning CNN • The workhorse of Deep Learning • CNN revolution started with LeCun (1998)—outperformed other methods on handwritten digit MNIST data. • CNN learns object defining features. 59 LeCun, Y., Bottou, L., Bengio, Y.,& Haffner, P. (1998). Gradient-based learning applied to document recognition. Proceedings of the IEEE, 86(11), 2278-2324. Fig. 1. LeCun (1998) architecture. Fig. 2. Feature learning in CNN.
Evolution of Deep Learning AlexNet (2012) New estimation techniques 60 • Performed best on ImageNet data— ILSVRC 2012 winner. • A difficult dataset with more than 1000 categories (labels). • Similar to LeNet-5 with 5 conv and 3 dense layers. But with • Max Pooling • ReLU nonlinearity • Dropout regularization • Data augmentation. Krizhevsky, A., Sutskever, I.,& Hinton, G. E. (2012). Imagenet classification with deep convolutional neural networks. In Advances in neural information processing systems (pp. 1097-1105).
Evolution of Deep Learning GoogLeNet (2014) Inception module • Introduced the idea that CNN layers can be stacked in serial and parallel. • Has 22 layer CNN and was the winner of ILSVRC 2014. • Let the model decide on the conv. size, e.g. 3x3 or 5x5. • Puts each convolution in parallel • Concatenate the resulting feature maps before going to the next layer. 61 Image source: http://slazebni.cs.illinois.edu/spring17/lec01_cnn_architectures.pdfSzegedy, C., Liu, W., Jia, Y., Sermanet, P., Reed, S., Anguelov, D., ...&Rabinovich, A. (2015). Going deeper with convolutions (2014). arXiv preprint arXiv:1409.4842, 7.
Evolution of Deep Learning Microsoft’s ResNet (2015) Residual Network • Went aggressive on adding layers. • Evaluated depth up to 152 layers on ImageNet—8x deeper than VGG nets but still lower complexity. • How deep can we go? 62
Evolution of Deep Learning Microsoft’s ResNet (2015) Residual Network • How deep can we go? With more layers • Training and test accuracy drops. • Degradation due to difficulty in optimization. • Introduced Residual Network • Residual network idea: add additional information (the conv transformation F(x)) in input data and pass to next layer. • Traditional CNNs: we learn a completely different transformation F(x) and pass it on for more transformation. • The authors found residual network is easier to optimize in very deep networks. 63 Fig. 1. Training error (left) and test error (right) on CIFAR-10 with 20- and 50- layer ”plain” networks. The deeper network has higher training error, and thus test error. Fig. 2. Residual learning: a building block. He, K., Zhang, X., Ren, S.,&Sun, J. (2016). Deep residual learning for image recognition. In Proceedings of the IEEE conference on computer vision and pattern recognition (pp. 770-778).
Evolution of Deep Learning Capsules (2017) Going to the next level • CNNs do not understand spatial relationships between features. • Come Capsules • preserves hierarchical pose relationships between object parts. • makes model understand a new view is just another view of same thing. • Performance • Cut error rate by 45%. • Used a fraction of the data compared to a CNN. 64 Fig. 1. For CNN, the position of features do not matter. Image source: https://medium.com/ai³-theory-practice-business/understanding- hintons-capsule-networks-part-i-intuition-b4b559d1159b Sabour, S., Frosst, N.,&Hinton, G. E. (2017). Dynamic routing between capsules. In Advances in Neural Information Processing Systems (pp. 3859-3869). Fig. 2. Capsules understand all images are the same object.
Evolution of Deep Learning We learned.. 65
Evolution of Deep Learning In summary, we learned • Problem to be broken into pieces (at nodes). • Non-linear decision makers. • Challenges met • Overfitting: Dropout • Vanishing gradient: New activations • Scaled Exponential Linear Units—will bring FNN to forefront. • Capsules—more closer to how brain works. 66
Evolution of Deep Learning In summary, we learned • Multimodal models with DBM. • LSTM+CNN for attention based model. • Inception: Let model figure conv size. • Residual network: Can learn deeper. 67 Yellow, flower
Evolution of Deep Learning Thank you! 68
Evolution of Deep Learning Why is non-linear activation required? 69 !" !# !$ %& Given ! ' " = ) " ! + + " , " = - " (' " ) ' # = ) # , " + + # , # = - # (' # ) Layer-1 Layer-2 ' # = ) # , " + + # = ) # ' " + + # = ) # () " ! + + " ) + + # = ) # ) " ! + () # + " + + # ) = )′! + +′ ⇒ ' # ~ ! ⇒ ' 4 ~ ! ⋮ Any number of layers collapse to one. Processed information transfer due to non-linear activation If this activation is linear, i.e. , " = ' " , then it becomes equivalent to passing the original input ! to the next layer.

More Related Content

PPTX
ppt on machine learning to deep learning (1).pptx
byAnweshaGarima
 
PDF
Neural Networks: Multilayer Perceptron
byMostafa G. M. Mostafa
 
PPTX
Introduction to Deep learning
byleopauly
 
PDF
Deep learning for real life applications
byAnas Arram, Ph.D
 
PDF
Recurrent Neural Networks, LSTM and GRU
byananth
 
PPTX
Machine learning
byAyesha Ahsan khan
 
PPTX
Deep learning
byHatim EL-QADDOURY
 
PPTX
Lecture 18: Gaussian Mixture Models and Expectation Maximization
bybutest
 
ppt on machine learning to deep learning (1).pptx
byAnweshaGarima
 
Neural Networks: Multilayer Perceptron
byMostafa G. M. Mostafa
 
Introduction to Deep learning
byleopauly
 
Deep learning for real life applications
byAnas Arram, Ph.D
 
Recurrent Neural Networks, LSTM and GRU
byananth
 
Machine learning
byAyesha Ahsan khan
 
Deep learning
byHatim EL-QADDOURY
 
Lecture 18: Gaussian Mixture Models and Expectation Maximization
bybutest
 

What's hot

PDF
Gradient-based optimization for Deep Learning: a short introduction
byChristian Perone
 
PPTX
Deep Learning With Neural Networks
byAniket Maurya
 
PPTX
Deep neural networks
bySi Haem
 
PDF
Introduction to Recurrent Neural Network
byYan Xu
 
PPTX
04 Multi-layer Feedforward Networks
byTamer Ahmed Farrag, PhD
 
PDF
Nature-inspired algorithms
byLars Marius Garshol
 
PPTX
Introduction to Machine Learning
bySujith Jayaprakash
 
PDF
Neural Networks: Self-Organizing Maps (SOM)
byMostafa G. M. Mostafa
 
PPTX
Deep Learning for Machine Translation
byMatīss ‎‎‎‎‎‎‎  
 
PDF
Human Action Recognition
byNAVER Engineering
 
PPTX
Reinforcement Learning : A Beginners Tutorial
byOmar Enayet
 
PPTX
Rnn & Lstm
bySubash Chandra Pakhrin
 
PPTX
Artifical Neural Network and its applications
bySangeeta Tiwari
 
PPTX
Machine learning and linear regression programming
bySoumya Mukherjee
 
PDF
Artificial Intelligence overview (by impulse)
bySoftware in Brussels
 
PPTX
INTRODUCTION TO MACHINE LEARNING.pptx
byAbhigyanMishra17
 
PPT
neural networks
byInstitute of Technology Telkom
 
PPTX
Unit 2 unsupervised learning.pptx
byDr.Shweta
 
PPTX
Machine learning ppt
byPoojamanic
 
PPT
Unit I & II in Principles of Soft computing
bySivagowry Shathesh
 
Gradient-based optimization for Deep Learning: a short introduction
byChristian Perone
 
Deep Learning With Neural Networks
byAniket Maurya
 
Deep neural networks
bySi Haem
 
Introduction to Recurrent Neural Network
byYan Xu
 
04 Multi-layer Feedforward Networks
byTamer Ahmed Farrag, PhD
 
Nature-inspired algorithms
byLars Marius Garshol
 
Introduction to Machine Learning
bySujith Jayaprakash
 
Neural Networks: Self-Organizing Maps (SOM)
byMostafa G. M. Mostafa
 
Deep Learning for Machine Translation
byMatīss ‎‎‎‎‎‎‎  
 
Human Action Recognition
byNAVER Engineering
 
Reinforcement Learning : A Beginners Tutorial
byOmar Enayet
 
Rnn & Lstm
bySubash Chandra Pakhrin
 
Artifical Neural Network and its applications
bySangeeta Tiwari
 
Machine learning and linear regression programming
bySoumya Mukherjee
 
Artificial Intelligence overview (by impulse)
bySoftware in Brussels
 
INTRODUCTION TO MACHINE LEARNING.pptx
byAbhigyanMishra17
 
neural networks
byInstitute of Technology Telkom
 
Unit 2 unsupervised learning.pptx
byDr.Shweta
 
Machine learning ppt
byPoojamanic
 
Unit I & II in Principles of Soft computing
bySivagowry Shathesh
 

Similar to Evolution of Deep Learning and new advancements

PDF
Introduction to Deep Learning: Concepts, Architectures, and Applications
byAmr Rashed
 
DOCX
Case study on deep learning
byHarshitBarde
 
PPTX
Deep Learning Tutorial
byAmr Rashed
 
PPTX
Deep learning tutorial 9/2019
byAmr Rashed
 
PDF
Deep Learning, an interactive introduction for NLP-ers
byRoelof Pieters
 
PPTX
Lecture 1 (Introduction to Deep Learning).pptx
byBilalKhan316808
 
PPTX
Deep Learning: Towards General Artificial Intelligence
byRukshan Batuwita
 
PPTX
Deep learning from a novice perspective
byAnirban Santara
 
PDF
MLIP - Chapter 3 - Introduction to deep learning
byCharles Deledalle
 
PPTX
Deep Learning Sample Class (Jon Lederman)
byJon Lederman
 
PPT
Introduction_to_DEEP_LEARNING.ppt
bySwatiMahale4
 
PDF
An Introduction to Deep Learning
byPoo Kuan Hoong
 
PPT
Introduction_to_DEEP_LEARNING.sfsdafsadfsadfsdafsdppt
byNaiduSetti
 
PPT
Introduction_to_DEEP_LEARNING ppt 101ppt
bysathyanarayanakb1
 
PDF
DSRLab seminar Introduction to deep learning
byPoo Kuan Hoong
 
PDF
Unraveling Information about Deep Learning
byIRJET Journal
 
PDF
Big Data Malaysia - A Primer on Deep Learning
byPoo Kuan Hoong
 
PPTX
GDSC Introduction to Deep Learning Workshop
byssuser540861
 
PPT
DEEP LEARNING PPT aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa
byRRamya22
 
PPTX
HML: Historical View and Trends of Deep Learning
byYan Xu
 
Introduction to Deep Learning: Concepts, Architectures, and Applications
byAmr Rashed
 
Case study on deep learning
byHarshitBarde
 
Deep Learning Tutorial
byAmr Rashed
 
Deep learning tutorial 9/2019
byAmr Rashed
 
Deep Learning, an interactive introduction for NLP-ers
byRoelof Pieters
 
Lecture 1 (Introduction to Deep Learning).pptx
byBilalKhan316808
 
Deep Learning: Towards General Artificial Intelligence
byRukshan Batuwita
 
Deep learning from a novice perspective
byAnirban Santara
 
MLIP - Chapter 3 - Introduction to deep learning
byCharles Deledalle
 
Deep Learning Sample Class (Jon Lederman)
byJon Lederman
 
Introduction_to_DEEP_LEARNING.ppt
bySwatiMahale4
 
An Introduction to Deep Learning
byPoo Kuan Hoong
 
Introduction_to_DEEP_LEARNING.sfsdafsadfsadfsdafsdppt
byNaiduSetti
 
Introduction_to_DEEP_LEARNING ppt 101ppt
bysathyanarayanakb1
 
DSRLab seminar Introduction to deep learning
byPoo Kuan Hoong
 
Unraveling Information about Deep Learning
byIRJET Journal
 
Big Data Malaysia - A Primer on Deep Learning
byPoo Kuan Hoong
 
GDSC Introduction to Deep Learning Workshop
byssuser540861
 
DEEP LEARNING PPT aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa
byRRamya22
 
HML: Historical View and Trends of Deep Learning
byYan Xu
 

Recently uploaded

PDF
"Painless Major Upgrade: A Strategy for Updating Large Codebases", Andrii Yat...
byFwdays
 
PDF
How to build hackthon projects from ZERO!
byishantyadav1111
 
PDF
Peculiar Findings Around CEX Activity and ETH Price
bytobbymnbvcxz
 
PDF
"When every team does things "right", but together it turns into chaos", Yozh...
byFwdays
 
PDF
Bettersize | BeSEC Series Product Brochure
byBettersize Instruments
 
PDF
Post-Hackathon-Learnings-Maximizing-Impact-Beyond-the-Event.pdf
byishantyadav1111
 
PPTX
INSY_7213_Theme Sessions 47 & 48 Advanced databases.pptx
bystormzy56
 
PPTX
The Lex Wire Precedent: A Technical Standard for Machine-Mediated Authority ...
byJeff Howell
 
PDF
Transcript: What Thema can do: Leveraging metadata to support the discoverabi...
byBookNet Canada
 
PDF
Chapter 3 Cryptography and encryption techniques.pdf
byGetnet Tigabie Askale -(GM)
 
PDF
AI and Zero Trust: What it takes to do it right
byMark Simos
 
PDF
Transcript: EU regulations for the North American book supply chain - Tech Fo...
byBookNet Canada
 
PDF
7 Essential Types of Penetration Testing Services Every Business Should Under...
bypandeydevika621
 
PDF
Parental Control App for Phones_ The Complete 2026 Guide for Safer, Smarter P...
byRyan Cooper
 
PDF
What Thema can do: Leveraging metadata to support the discoverability of Firs...
byBookNet Canada
 
PDF
Taxonomy Alignment for SDG Tagging - ASHA Case Study
byEnterprise Knowledge
 
PDF
Computer-Based Training (CBT) The Backbone of Modern Technical & Defence Trai...
bycomputerbasedtrainin1
 
PDF
Dev Dives: Build and deploy agentic automations - the unified way
byUiPathCommunity
 
PPTX
Software Engineering in the Age of AI Agents
byHusseinMalikMammadli
 
PDF
Certified AI-Empowered SAFe Release Train Engineer.pdf
byMarc Entsminger SPC6, RTE, SSM, SA, SDP
 
"Painless Major Upgrade: A Strategy for Updating Large Codebases", Andrii Yat...
byFwdays
 
How to build hackthon projects from ZERO!
byishantyadav1111
 
Peculiar Findings Around CEX Activity and ETH Price
bytobbymnbvcxz
 
"When every team does things "right", but together it turns into chaos", Yozh...
byFwdays
 
Bettersize | BeSEC Series Product Brochure
byBettersize Instruments
 
Post-Hackathon-Learnings-Maximizing-Impact-Beyond-the-Event.pdf
byishantyadav1111
 
INSY_7213_Theme Sessions 47 & 48 Advanced databases.pptx
bystormzy56
 
The Lex Wire Precedent: A Technical Standard for Machine-Mediated Authority ...
byJeff Howell
 
Transcript: What Thema can do: Leveraging metadata to support the discoverabi...
byBookNet Canada
 
Chapter 3 Cryptography and encryption techniques.pdf
byGetnet Tigabie Askale -(GM)
 
AI and Zero Trust: What it takes to do it right
byMark Simos
 
Transcript: EU regulations for the North American book supply chain - Tech Fo...
byBookNet Canada
 
7 Essential Types of Penetration Testing Services Every Business Should Under...
bypandeydevika621
 
Parental Control App for Phones_ The Complete 2026 Guide for Safer, Smarter P...
byRyan Cooper
 
What Thema can do: Leveraging metadata to support the discoverability of Firs...
byBookNet Canada
 
Taxonomy Alignment for SDG Tagging - ASHA Case Study
byEnterprise Knowledge
 
Computer-Based Training (CBT) The Backbone of Modern Technical & Defence Trai...
bycomputerbasedtrainin1
 
Dev Dives: Build and deploy agentic automations - the unified way
byUiPathCommunity
 
Software Engineering in the Age of AI Agents
byHusseinMalikMammadli
 
Certified AI-Empowered SAFe Release Train Engineer.pdf
byMarc Entsminger SPC6, RTE, SSM, SA, SDP
 

Evolution of Deep Learning and new advancements

  • 1.
    Evolution of DeepLearning: New Methods and Applications Chitta Ranjan, Ph.D. Pandora Media. Feb 15, 2018 nk.chitta.ranjan@gmail.com 1
  • 2.
    Evolution of DeepLearning Outline • Background • Challenges • Solutions 2
  • 3.
    Evolution of DeepLearning How does our brain work? • How do we know where the ball will fall? 3
  • 4.
    Evolution of DeepLearning How does our brain work? • How do we know where the ball will fall? • Do we solve these equations in our head? No. 4 ! = #$ % sin% ) 2+ , = #$ % sin 2) + - = 2#$ sin ) +
  • 5.
    Evolution of DeepLearning How does our brain work? • How do we know where the ball will fall? • Do we solve these equations in our head? No. • Perhaps we break the problem into pieces and solve it. 5
  • 6.
    Evolution of DeepLearning Traditional block model One model for the whole problem 6 • One solver to solve it all. • Has limitation for complex problems. ! = #$ % sin% ) 2+ , = #$ % sin 2) + - = 2#$ sin ) +
  • 7.
    Evolution of DeepLearning Neural Network 7 • A neuron solves a piece of the big problem. • Understand the inter-relationships between the pieces. • Merge the small solutions to find the solution.
  • 8.
    Evolution of DeepLearning Neural Network 8 • Can we have bidirectional connections?
  • 9.
    Evolution of DeepLearning Neural Network 9 • Can we have bidirectional connections? • Can we have edges connecting neurons in the same layer?
  • 10.
    Evolution of DeepLearning Neural Network 10 • Can we have bidirectional connections? • Can we have edges connecting neurons in the same layer? • Is Neural Network an Ensemble model?
  • 11.
    Evolution of DeepLearning Birth of Neural Network 11
  • 12.
    Evolution of DeepLearning Perceptron (1958) 12 Rosenblatt, F. (1960). Perceptron simulation experiments. Proceedings of the IRE, 48(3), 301-309.
  • 13.
    Evolution of DeepLearning Perceptron (1958) ∑ !" !# !$ %" %# %$ = ∑%(!( +1 −1 Non-linear 13 • A non-linear computation cell. • Non-linear cells became the building block of Neural Networks. Rosenblatt, F. (1960). Perceptron simulation experiments. Proceedings of the IRE, 48(3), 301-309.
  • 14.
    Evolution of DeepLearning Multi-layer Perceptron (1986) 14 • Nodes are Perceptrons. • Layers of Perceptrons. • Relationships (weights on arcs) found using newly-developed Backpropagation. The nonlinear part is critical. Without it, it is equivalent the big block model. Rumelhart, David E., Geoffrey E. Hinton, and R. J. Williams. "Learning Internal Representations by Error Propagation". David E. Rumelhart, James L. McClelland, and the PDP research group. (editors), Parallel distributed processing: Explorations in the microstructure of cognition, Volume 1: Foundation. MIT Press, 1986.
  • 15.
    Evolution of DeepLearning Multi-layer Perceptron (1986) 15 • Nodes are Perceptrons. • Layers of Perceptrons. • Relationships (weights on arcs) found using newly-developed Backpropagation. The nonlinear part is critical. Without it, it is equivalent the big block model.
  • 16.
    Evolution of DeepLearning Multi-layer Perceptron (1986) 16 • Nodes are Perceptrons. • Layers of Perceptrons. • Relationships (weights on arcs) found using newly-developed Backpropagation. The nonlinear part is critical. Without it, it is equivalent the big block model. Rumelhart, David E., Geoffrey E. Hinton, and R. J. Williams. "Learning Internal Representations by Error Propagation". David E. Rumelhart, James L. McClelland, and the PDP research group. (editors), Parallel distributed processing: Explorations in the microstructure of cognition, Volume 1: Foundation. MIT Press, 1986.
  • 17.
    Evolution of DeepLearning Some definitions 17 Activation function Neuron/node Layer Network depth Networkwidth Weight/ connection/arc Input Output
  • 18.
    Evolution of DeepLearning We learned.. 18
  • 19.
    Evolution of DeepLearning So far we learned • Problem to be broken into pieces (at nodes). • Non-linear decision makers. 19
  • 20.
    Evolution of DeepLearning Timeline 20
  • 21.
    Evolution of DeepLearning 1980 Capsules SeLU 2017 Dropout 2012 ReLU ResNet, 152 layers GoogLeNet, 22 layers* VGG Net, 19 layers AlexNet, 8 layers Layers Perceptron 1958 1969 Perceptron criticized— XOR problem ∑ !" !# !$ %" %# %$ = ∑%(!( +1 −1 1987 1986 Multilayer Perceptron— Backpropagation Inputs Outputs Forward direction Backward direction AI Winter I (74-80) 2006 CNN for handwritten image 1998 CNN—Neocognitron AI Winter II (87-93) 1997 LSTM DBM—Faster learning *The overall number of layers (independent building blocks) used for the construction of the network is about 100. 21 MNIST
  • 22.
    Evolution of DeepLearning Challenges Computation GPU! 22
  • 23.
    Evolution of DeepLearning Challenges Computation GPU! 23
  • 24.
    Evolution of DeepLearning Challenges Estimation Overfitting Vanishing gradient Dropout Activation functions 24
  • 25.
    Evolution of DeepLearning Dropout 25
  • 26.
    Evolution of DeepLearning Let’s take a step back.. 26 ⋮ ⋮ ⋮ ⋮ ⋮ • Learning becomes difficult in large networks. • Off-the-shelf L1/L2 regularization was used. • They did not work.
  • 27.
    Evolution of DeepLearning Silenced by L1 (L2) • Regularization happens based on the predictive/information capability of a node. 27
  • 28.
    Evolution of DeepLearning Silenced by L1 (L2) • Regularization happens based on the predictive/information capability of a node. • The weak nodes are always (deterministically) thrown out. • Weak nodes do not get a say. 28 *Loosely speaking
  • 29.
    Evolution of DeepLearning Co-adaptation • Nodes co-adapt. • Rely on presence of another node. • Few nodes do the heavy lifting while others do nothing. 29
  • 30.
    Evolution of DeepLearning 30 Wide networks doesn’t really help.
  • 31.
    Evolution of DeepLearning Dropout (2014) • Presence of node is a matter of chance 31 Silencing Co-adaptation Srivastava, N., Hinton, G., Krizhevsky, A., Sutskever, I.,& Salakhutdinov, R. (2014). Dropout: A simple way to prevent neural networks from overfitting. The Journal of Machine Learning Research, 15(1), 1929-1958.
  • 32.
    Evolution of DeepLearning Dropout with Gaussian gate (2017) • Regular dropout: multiply activations with Bernoulli RVs. • Generalization: Multiply with any RV. 32 !" !# !$ !% ~'(!)(+) ~'(!)(+) ~'(!)(+) ~'(!)(+) Molchanov, D., Ashukha, A.,&Vetrov, D. (2017). Variational dropout sparsifies deep neural networks. arXiv preprint arXiv:1701.05369.
  • 33.
    Evolution of DeepLearning Dropout with Gaussian gate (2017) • Regular dropout: multiply activations with Bernoulli RVs. • Generalization: Multiply with any RV. • Gaussian gates is found to improve dropout’s performance. 33 !" !# !$ !% ~'(!)(+) ~'(!)(+) ~'(!)(+) ~'(!)(+) ~-(0,1) ~-(0,1) ~-(0,1) ~-(0,1) Molchanov, D., Ashukha, A.,&Vetrov, D. (2017). Variational dropout sparsifies deep neural networks. arXiv preprint arXiv:1701.05369.
  • 34.
    Evolution of DeepLearning Activation functions 34
  • 35.
    Evolution of DeepLearning Vanishing Gradient in Deep Networks 35 ⋮ ⋮ ⋮ ⋮ ⋮ """" • Learning was still difficult in large networks. • Activation functions at the time caused the gradient to vanish in lower layers. • Difficult to learn weights. Backpropagation
  • 36.
    Evolution of DeepLearning 36 Deep networks doesn’t really help.
  • 37.
    Evolution of DeepLearning Vanishing gradient • Because sigmoid and tanh functions had saturation regions on both sides. 37 sigmoid tanh
  • 38.
    Evolution of DeepLearning New Activations Resolving vanishing gradient Rectified Linear Unit (ReLU), 2013 38 Maas, A. L., Hannun, A. Y.,&Ng, A. Y. (2013, June). Rectifier nonlinearities improve neural network acoustic models. In Proc. icml (Vol. 30, No. 1, p. 3). Clevert, D. A., Unterthiner, T.,&Hochreiter, S. (2015). Fast and accurate deep network learning by exponential linear units (elus). arXiv preprint arXiv:1511.07289. Exponential Linear Unit (ELU), 2016 Saturation region on only one side (left) for these activations.
  • 39.
    Evolution of DeepLearning We learned.. 39
  • 40.
    Evolution of DeepLearning So far we learned • Problem to be broken into pieces (at nodes). • Non-linear decision makers. • Challenges met • Overfitting: Dropout • Vanishing gradient: New activations 40
  • 41.
    Evolution of DeepLearning Model types 41
  • 42.
    Evolution of DeepLearning Types of Models • Unsupervised • Deep Belief Networks (DBN) • Supervised • Feed-forward Neural Network (FNN) • Recurrent Neural Network (RNN) • Convolutional Neural Network (CNN) 42
  • 43.
    Evolution of DeepLearning Deep Belief Networks (DBN) 43
  • 44.
    Evolution of DeepLearning Restricted Boltzmann Machine (RBM) • Has two layers • Visible: Think of input data • Hidden: Think of latent factors • Learn features from data that can generate the same training data. 44 HiddenVisible FeaturesData Data
  • 45.
    Evolution of DeepLearning Restricted Boltzmann Machine (RBM) • Has two layers • Visible: Think of input data • Hidden: Think of latent factors • Learn features from data that can generate the same training data. • Bi-directional node relationship. 45 HiddenVisible FeaturesData
  • 46.
    Evolution of DeepLearning Deep Belief Nets (2006) Stacked RBMs/Autoencoders 46 • Fast greedy algorithm—learn one layer at a time. • Feature extraction and Unsupervised pre- training. • MNIST digit classification: Yielded much better accuracy. • Used in sensor data. • Was dying technology after vanishing gradient was resolved with new ReLU, ELU activations. Hinton, G. E., Osindero, S.,&Teh, Y. W. (2006). A fast learning algorithm for deep belief nets. Neural computation, 18(7), 1527-1554.
  • 47.
    Evolution of DeepLearning Multimodal Modeling (2012) Comeback of DBN Image data Text data 47 Yellow, flower + • Used to create fused representations by combining features across modalities. • Representations useful for classification and information retrieval. • Works even if • Some data modalities are missing, e.g. image- text. • Different observation frequencies, e.g. sensor data. Srivastava, N.,& Salakhutdinov, R. R. (2012). Multimodal learning with deep boltzmann machines. In Advances in neural information processing systems (pp. 2222-2230). Liu, Z., Zhang, W., Quek, T. Q.,&Lin, S. (2017, March). Deep fusion of heterogeneous sensor data. In Acoustics, Speech and Signal Processing (ICASSP), 2017 IEEE International Conference on (pp. 5965-5969). IEEE.
  • 48.
    Evolution of DeepLearning Feed-forward Neural Network (FNN) 48
  • 49.
    Evolution of DeepLearning FNN 49 • One of the earliest type of NN— Multilayer Perceptrons (MLP). • No success story—learning more than 4 layer deep network was difficult. • Typically only used as last (top) layers in other networks. • Then came SELU activation.
  • 50.
    Evolution of DeepLearning Scaled Exponential Linear Units (SELU), 2017 Self-normalizing Neural Networks. New life for FNNs. 50 Klambauer, G., Unterthiner, T., Mayr, A.,&Hochreiter, S. (2017). Self-normalizing neural networks. In Advances in Neural Information Processing Systems (pp. 972-981). • Activations automatically converge to zero mean and unit variance. • Converges in presence of noise and perturbations. • Allows • train deep networks with many layers, • employ strong regularization schemes, and • to make learning highly robust.
  • 51.
    Evolution of DeepLearning Recurrent Neural Network (RNN) 51
  • 52.
    Evolution of DeepLearning RNN Image source: http://colah.github.io/posts/2015-08-Understanding-LSTMs/ 52 • For temporal data. • An RNN passes a message to a successor.
  • 53.
    Evolution of DeepLearning RNN Image source: http://colah.github.io/posts/2015-08-Understanding-LSTMs/ 53 • For temporal data. • An RNN passes a message to a successor. • Learns dependencies with past.
  • 54.
    Evolution of DeepLearning RNN Image source: http://colah.github.io/posts/2015-08-Understanding-LSTMs/ 54 *Bengio, Y., Simard, P.,&Frasconi, P. (1994). Learning long-term dependencies with gradient descent is difficult. IEEE transactions on neural networks, 5(2), 157-166. • For temporal data. • An RNN passes a message to a successor. • Learns dependencies with past. • Failed to learn long-term dependencies*. • Then came LSTM.
  • 55.
    Evolution of DeepLearning Long short-term memory (LSTM), 1997 55 Image source: http://colah.github.io/posts/2015-08-Understanding-LSTMs/ RNN LSTM Hochreiter, S.,&Schmidhuber, J. (1997). Long short-term memory. Neural computation, 9(8), 1735-1780. Cho, K., Van Merriënboer, B., Gulcehre, C., Bahdanau, D., Bougares, F., Schwenk, H.,&Bengio, Y. (2014). Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv preprint arXiv:1406.1078. • A special kind of RNN capable of learning long-term dependencies. • The added gates regulate addition or removal of passing information. • Found powerful in: • natural language processing, • unsegmented connected handwriting recognition • speech recognition • Gated Recurrent Units (GRUs), 2014 • Fewer parameters than LSTM. • Performance comparable or lower than LSTM (so far).
  • 56.
    Evolution of DeepLearning Attention Based Model (2015) • CNN together with LSTM. • Automatically learns • to fix gaze on salient objects. • Object alignments. • Object relationships with sequence of words. 56 Xu, K., Ba, J., Kiros, R., Cho, K., Courville, A., Salakhudinov, R., ...&Bengio, Y. (2015, June). Show, attend and tell: Neural image caption generation with visual attention. In International Conference on Machine Learning (pp. 2048-2057). Fig. 1. Attention model architecture. Fig. 2. Examples of attending to the correct object (white indicates the attended regions, underlines indicated the corresponding word).
  • 57.
    Evolution of DeepLearning Convolutional Neural Network (CNN) 57
  • 58.
    Evolution of DeepLearning CNN • The workhorse of Deep Learning • CNN revolution started with LeCun (1998)—outperformed other methods on handwritten digit MNIST data. 58 LeCun, Y., Bottou, L., Bengio, Y.,&Haffner, P. (1998). Gradient-based learning applied to document recognition. Proceedings of the IEEE, 86(11), 2278-2324. Fig. 1. LeCun (1998) architecture.
  • 59.
    Evolution of DeepLearning CNN • The workhorse of Deep Learning • CNN revolution started with LeCun (1998)—outperformed other methods on handwritten digit MNIST data. • CNN learns object defining features. 59 LeCun, Y., Bottou, L., Bengio, Y.,& Haffner, P. (1998). Gradient-based learning applied to document recognition. Proceedings of the IEEE, 86(11), 2278-2324. Fig. 1. LeCun (1998) architecture. Fig. 2. Feature learning in CNN.
  • 60.
    Evolution of DeepLearning AlexNet (2012) New estimation techniques 60 • Performed best on ImageNet data— ILSVRC 2012 winner. • A difficult dataset with more than 1000 categories (labels). • Similar to LeNet-5 with 5 conv and 3 dense layers. But with • Max Pooling • ReLU nonlinearity • Dropout regularization • Data augmentation. Krizhevsky, A., Sutskever, I.,& Hinton, G. E. (2012). Imagenet classification with deep convolutional neural networks. In Advances in neural information processing systems (pp. 1097-1105).
  • 61.
    Evolution of DeepLearning GoogLeNet (2014) Inception module • Introduced the idea that CNN layers can be stacked in serial and parallel. • Has 22 layer CNN and was the winner of ILSVRC 2014. • Let the model decide on the conv. size, e.g. 3x3 or 5x5. • Puts each convolution in parallel • Concatenate the resulting feature maps before going to the next layer. 61 Image source: http://slazebni.cs.illinois.edu/spring17/lec01_cnn_architectures.pdfSzegedy, C., Liu, W., Jia, Y., Sermanet, P., Reed, S., Anguelov, D., ...&Rabinovich, A. (2015). Going deeper with convolutions (2014). arXiv preprint arXiv:1409.4842, 7.
  • 62.
    Evolution of DeepLearning Microsoft’s ResNet (2015) Residual Network • Went aggressive on adding layers. • Evaluated depth up to 152 layers on ImageNet—8x deeper than VGG nets but still lower complexity. • How deep can we go? 62
  • 63.
    Evolution of DeepLearning Microsoft’s ResNet (2015) Residual Network • How deep can we go? With more layers • Training and test accuracy drops. • Degradation due to difficulty in optimization. • Introduced Residual Network • Residual network idea: add additional information (the conv transformation F(x)) in input data and pass to next layer. • Traditional CNNs: we learn a completely different transformation F(x) and pass it on for more transformation. • The authors found residual network is easier to optimize in very deep networks. 63 Fig. 1. Training error (left) and test error (right) on CIFAR-10 with 20- and 50- layer ”plain” networks. The deeper network has higher training error, and thus test error. Fig. 2. Residual learning: a building block. He, K., Zhang, X., Ren, S.,&Sun, J. (2016). Deep residual learning for image recognition. In Proceedings of the IEEE conference on computer vision and pattern recognition (pp. 770-778).
  • 64.
    Evolution of DeepLearning Capsules (2017) Going to the next level • CNNs do not understand spatial relationships between features. • Come Capsules • preserves hierarchical pose relationships between object parts. • makes model understand a new view is just another view of same thing. • Performance • Cut error rate by 45%. • Used a fraction of the data compared to a CNN. 64 Fig. 1. For CNN, the position of features do not matter. Image source: https://medium.com/ai³-theory-practice-business/understanding- hintons-capsule-networks-part-i-intuition-b4b559d1159b Sabour, S., Frosst, N.,&Hinton, G. E. (2017). Dynamic routing between capsules. In Advances in Neural Information Processing Systems (pp. 3859-3869). Fig. 2. Capsules understand all images are the same object.
  • 65.
    Evolution of DeepLearning We learned.. 65
  • 66.
    Evolution of DeepLearning In summary, we learned • Problem to be broken into pieces (at nodes). • Non-linear decision makers. • Challenges met • Overfitting: Dropout • Vanishing gradient: New activations • Scaled Exponential Linear Units—will bring FNN to forefront. • Capsules—more closer to how brain works. 66
  • 67.
    Evolution of DeepLearning In summary, we learned • Multimodal models with DBM. • LSTM+CNN for attention based model. • Inception: Let model figure conv size. • Residual network: Can learn deeper. 67 Yellow, flower
  • 68.
    Evolution of DeepLearning Thank you! 68
  • 69.
    Evolution of DeepLearning Why is non-linear activation required? 69 !" !# !$ %& Given ! ' " = ) " ! + + " , " = - " (' " ) ' # = ) # , " + + # , # = - # (' # ) Layer-1 Layer-2 ' # = ) # , " + + # = ) # ' " + + # = ) # () " ! + + " ) + + # = ) # ) " ! + () # + " + + # ) = )′! + +′ ⇒ ' # ~ ! ⇒ ' 4 ~ ! ⋮ Any number of layers collapse to one. Processed information transfer due to non-linear activation If this activation is linear, i.e. , " = ' " , then it becomes equivalent to passing the original input ! to the next layer.