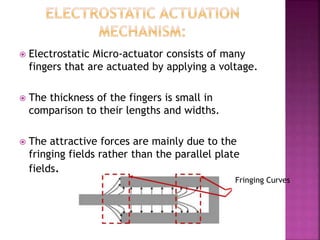
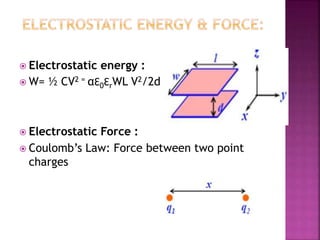
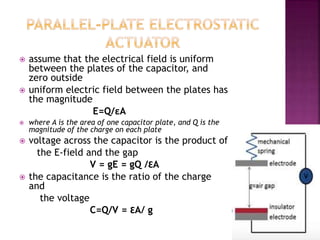
This document discusses microelectromechanical systems (MEMS) and electrostatic micro-actuators. It explains that MEMS integrate sensors, actuators and electronics on a silicon substrate using microfabrication technology. Electrostatic micro-actuators consist of thin fingers that are actuated by applying a voltage, generating an attractive electrostatic force due to fringing fields. The document derives equations for the electrostatic energy and force in a parallel plate capacitor model, showing that the force is independent of gap size. It describes the pull-in effect, where the gap decreases until reaching 2/3 of the original spacing, at which point the plates suddenly contact.

1. NIMI T
2nd Year MTech ECE
Pondicherry University

2.  It stands for micro electro mechanical
systems
 It is the integration of elements sensors
actuators and electronics on a common
silicon substrate
 Micro fabrication technology, for making
microscopic devices

3.  The actuator is an element which applies a
force to some object through a distance
 Various actuation mechanisms:
- Electrostatic actuation
-Thermal actuation
-Piezoelectric actuation
-Magnetic actuation

5.  A voltage is applied between metal plates to
induce opposite charges and Coulomb
attraction
Where
α fringing field factor Normally the flux lines inside
the capacitor are uniform and
parallel. But at the edges, the
flux lines are not straight and
bend slightly upward due to
the geometry. This is known as
fringing effect.

6.  Electrostatic Micro-actuator consists of many
fingers that are actuated by applying a voltage.
 The thickness of the fingers is small in
comparison to their lengths and widths.
 The attractive forces are mainly due to the
fringing fields rather than the parallel plate
fields.
Fringing Curves

7.  Electrostatic energy :
 W= ½ CV2 = αƐ0ƐrWL V2/2d
 Electrostatic Force :
 Coulomb’s Law: Force between two point
charges

8.  Low power dissipation.
 Can be designed to dissipate no power while
exerting a force.
 High power density at micro scale.
 Easy to fabricate.

9.  Scaling
 Noise & Efficiency
 Range of force, motion and frequency
 Repeatability
 Nonlinearity

10. MASS
UIUC
Examples
• Parallel Plate Capacitor
• Comb Drive Capacitor

11.  assume that the electrical field is uniform
between the plates of the capacitor, and
zero outside
 uniform electric field between the plates has
the magnitude
E=Q/εA
 where A is the area of one capacitor plate, and Q is the
magnitude of the charge on each plate
 voltage across the capacitor is the product of
the E-field and the gap
V = gE = gQ /ƐA
 the capacitance is the ratio of the charge
and
the voltage
C=Q/V = ƐA/ g

12. When the capacitor plates are fixed
The stored energy in the capacitor is given by
Fixed gap
Increasing charge

13. Charging the capacitor at zero gap and
lifting
 At zero gap, the electrical stored energy is zero
 The force between two plates with opposite charges +Q
and –Q depends on electric field setup by charges
 This field is
Ɛ= Q/εA
 The corresponding force is
F= (Q/2)Ɛ =Q2/2ƐA  This force is independent of g
 Now we pull upper plate by distance g
W(g) = F*g
= Q2g/2ƐA
Charge fixed,
Increasing gap

14. • Stored energy
• Force is derivative of energy with
respect to pertinent dimensional
variable
• Plug in the expression for capacitor
• We arrive at the expression for
force
C
Q
CVU
2
2
2
1
2
1

2
2
1
V
d
C
d
U
F






d
A
d
A
Q
Q
C



d
CV
V
d
A
d
U
F
2
2
2
2
1
2
1






15.  As the voltage bias increases from zero
across a pair of parallel plates, the distance
between such plates would decrease until
they reach 2/3 of the original spacing, at
which point the two plates would be
suddenly snapped into contact.
 This behavior is called the pull-in effect.