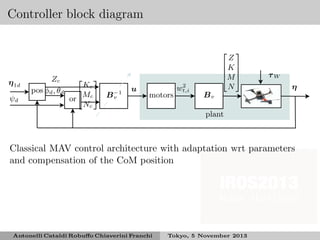
The document presents an experimental validation of an adaptive control scheme for quadrotor MAVs that is robust to uncertainties in mass, center of mass location, and external disturbances. The control scheme uses adaptive techniques to estimate unknown parameters and compensate for their effects. Experimental results show that the adaptive controller more accurately tracks a desired trajectory than a non-adaptive controller, especially when an additional weight is added to introduce parameter uncertainties. The adaptive controller maintains tracking accuracy even in the presence of external disturbances and unknown variations in vehicle parameters.

1. Experimental validation of a new adaptive
control scheme for quadrotors MAVs
Gianluca Antonelli† , Elisabetta Cataldi† ,
Paolo Robuffo Giordano⊕ , Stefano Chiaverini† , Antonio Franchi≀
† University
of Cassino and Southern Lazio, Italy
http://webuser.unicas.it/lai/robotica
⊕ CNRS at IRISA and Inria Bretagne Atlantique, France
http://www.irisa.fr/lagadic
≀ Max Planck Institute for Biol. Cybernetics, Germany
http://www.kyb.mpg.de/research/dep/bu/hri/
IROS 2013
Antonelli Cataldi Robuffo Chiaverini Franchi
Tokyo, 5 November 2013

2. Trajectory tracking control for quadrotor
Adaptive with respect to
uncertainty in total mass
uncertainty in Center Of Mass (CoM)
presence of 6-DOF external disturbances
Assumption: closed-loop orientation dynamics faster than
translational one
Stability analysis & numerical simulations1
Experimental results
1
Antonelli, Arrichiello, Chiaverini, Robuffo Giordano, “Adaptive
trajectory tracking for quadrotor MAVs in presence of parameter
uncertainties and external disturbances”, AIM 2013
Antonelli Cataldi Robuffo Chiaverini Franchi
Tokyo, 5 November 2013

3. Kinematics
body-fixed u, surge
xb
p, roll
Ob
q, pitch
η1
r, yaw
yb
v, sway
zb
w, heave
η1 =
η2 =
O
x
earth-fixed
x y z
φ θ ψ
ν 1 = RB η 1
I ˙
˙
ν 2 = T (η 2 )η 2
y
z
Antonelli Cataldi Robuffo Chiaverini Franchi
Tokyo, 5 November 2013
T
T

4. Dynamics
Mathematical model expressed in body-fixed frame
˙
M ν + C(ν)ν + τ W + g(RB ) = τ ,
I
beyond the common terms, we model
τW =
γ W ∈ R6 external disturbance
RB O 3×3
I
γW
O 3×3 RB
I
constant in the inertial frame (wind)
Antonelli Cataldi Robuffo Chiaverini Franchi
Tokyo, 5 November 2013

5. Dynamics -2Exploiting the linearity in the parameters
˙
Φ(ν, ν, RB )γ = τ
I
and rewriting with respect to the inertial frame while separating the
xy dynamics from z:
˙ ¨
Φxy (η, η, η )
γ = RI τ 1
B
˙ ¨
φz (η, η, η )
with γ ∈ R16 :
mass (1 parameter)
first moment of inertia (3 p.)
inertia tensor (6 p.)
τ =
τ1
τ2
external disturbance (6 p.)
Antonelli Cataldi Robuffo Chiaverini Franchi

0
0
 
Z 
= 
K 
 
M 

N
Tokyo, 5 November 2013

6. Thrust
Assuming CoM coincident with Ob
f2
2
τt,3
l
f3
ωt,2
f4
yb z
b
ωt,4
τt,4
4
τt,2
f1
Ob
ωt,3
3
2
fi = bωt,i
ωt,1
xb
1
O
y
τt,1
x
z
Antonelli Cataldi Robuffo Chiaverini Franchi
2
τt,i = dωt,i

0
 0

τ1 =  4

i=1


fi





l(f2 − f4 )

l(f1 − f3 )
τ2 = 
−τt,1 + τt,2 − τt,3 + τt,4
Tokyo, 5 November 2013

7. Mapping from the angular velocities to the force-torques
Assuming CoM of coordinates r C :
 
 2 
ωt,1
Z
2
K 
ωt,2 
  = Bv 

M 
ω 2 
t,3
2
N
ωt,4
with


b
b
b
b

0
b(l + rC,y )
0
−b(l − rC,y )

Bv = 
b(l + rC,x )

0
−b(l − rC,x )
0
−d
d
−d
d
CoM influences the mapping from thrust generated from the
motors to the vehicle forces/moments
Antonelli Cataldi Robuffo Chiaverini Franchi
Tokyo, 5 November 2013

8. Inverse mapping
Any controller determines a control action Zc Kc Mc Nc
projected onto the motor input u ∈ R4
 
Zc
 Kc 
u = B −1  
v 
Mc 
Nc
where B −1 ∈ R4×4 is
v

B −1
v
l − rC,x
 4bl
l − r
C,y


 4bl
= l + r
C,x

 4bl
 l + rC,y
4bl
0
1
2bl
0
1
−
2bl
Antonelli Cataldi Robuffo Chiaverini Franchi
1
2bl
0
1
−
2bl
0

l − rC,x
−
4dl 
l − rC,y 


4dl 
l + rC,x 

−
4dl 
l + rC,y 
4dl
Tokyo, 5 November 2013
T
further

9. Current inverse mapping
ˆ
When the CoM position estimate r C is affected
mapping becomes

1
0
 
 
Z
Zc
 rC,y
˜
1
K 
 Kc  
  = B v | B −1
   2
ˆ
r C v r C Mc  =  rC,x
M 
˜

0

2
N
Nc
0
0
by an error, the real

0
 
b˜C,y  Zc
r
 
0
2d   Kc 
b˜C,x  Mc 
r 
1 −

2d
Nc
0
1
0
wrong CoM estimate ⇒ a coupling from altitude and yaw control
actions onto roll and pitch dynamics
Antonelli Cataldi Robuffo Chiaverini Franchi
Tokyo, 5 November 2013

10. Controller block diagram

Z
K 
 
M 
N

η 1d
ψd
Zc
pos φd , θd


Kc
Mc  B −1
v
or
Nc
u
motors
2
wt,i
τW
η
Bv
plant
Classical MAV control architecture with adaptation wrt parameters
and compensation of the CoM position
Antonelli Cataldi Robuffo Chiaverini Franchi
Tokyo, 5 November 2013

11. Altitude controller
error
z = zd − z ∈ R
˜
˙
s z = z + λz z ∈ R
˜
˜
full version
1
ˆ
(φ γ + kvz sz )
cos φ cos θ z
˙
γ = K −1 φT sz
ˆ
γ,z z
Z =
ˆ
with γ ∈ R16
reduced version
1
(ˆz + kvz sz )
γ
cos φ cos θ
−1
= kγ,z sz
Z =
˙
γz
ˆ
ˆ
with γ z ∈ R1
the reduced version designed to compensate only for persistent
terms ⇒ null steady state error wrt a minimal set of parameters!
(λz > 0, kvz > 0, K γ,z > O, kγ,z > 0)
Antonelli Cataldi Robuffo Chiaverini Franchi
Tokyo, 5 November 2013

12. Horizontal controller
error
T
˜
η xy = xd − x yd − y ∈ R2
˙
˜
sxy = η xy + λxy η xy ∈ R2
˜
full version
reduced version
virtual input solutions of:
virtual input solutions of:
1
cφ sθ
ˆ
Rz (Φxy γ + kv,xy sxy )
=
−sφ
Z
˙
γ = K −1 ΦT sxy
ˆ
γ,xy xy
ˆ
with γ ∈ R16
1
cφ sθ
ˆ
Rz γ xy + kv,xy sxy
=
−sφ
Z
−1
˙
γ xy = kγ,xy sxy
ˆ
ˆ
with γ xy ∈ R2
again: the reduced version compensates only for persistent terms
⇒ null steady state error wrt a minimal set of parameters!
(λxy > 0, kv,xy > 0, K γ,xy > O, kγ,xy > 0)
Antonelli Cataldi Robuffo Chiaverini Franchi
Tokyo, 5 November 2013

13. Orientation controller
The inputs are the desired roll, pitch and yaw
The commanded forces map onto the real ones according to
K
=
M
N
=
=
b˜C,y
rC,y
˜
r
Zc +
Nc
2
2d
b˜C,x
rC,x
˜
r
Zc −
Nc
Mc +
2
2d
Nc
Kc +
˜
Neither the altitude nor the yaw control loop are affected by rC , thus both Zc
and Nc convergence to a steady state value
Roll and pitch control can be designed by considering the estimation error as
an external, constant, disturbance:
K
=
M
=
1
b
Zc + Nc rC,y
˜
2
d
1
b
Mc +
Zc − Nc rC,x
˜
2
d
Kc +
The disturbance value is unknown and its effect may be compensated by
resorting to several adaptive control laws well known in the literature
Antonelli Cataldi Robuffo Chiaverini Franchi
Tokyo, 5 November 2013

14. CoM estimation
PD control for roll and pitch =⇒ steady-state error because of the
wrong CoM estimate
A simple integral action can counteract this effect resulting a zero
steady-state error
˙
θ −θ
rC,x
ˆ
= −krC d
,
˙
φd − φ
rC,y
ˆ
krC > 0
As a byproduct, in absence of moment disturbance, the estimates
(ˆC,x , rC,y ) are driven towards the real CoM offsets (rC,x , rC,y )
r
ˆ
Antonelli Cataldi Robuffo Chiaverini Franchi
Tokyo, 5 November 2013

15. Stability analysis
˜
ˆ
Altitude controller: let γ = γ − γ and consider the Lyapunov function
˜
V (sz , γ ) =
m 2 1 T
˜
˜
s + γ K γ,z γ
2 z 2
Along the system trajectories
˙
˙
˙
˜
˜
z
z
˜
ˆ
V (sz , γ ) = sz m¨d − m¨ + mλz z − γ T K γ,z γ
˙
˜
= sz (φz γ − cos φ cos θZ) − γ T K γ,z γ = −kvz s2 ≤ 0
ˆ
z
State trajectories are bounded
Asymptotic stability can be further proven by resorting to Barbalat’s
Lemma as in classical adaptive control schemes
Similar machinery for the horizontal controller case
Antonelli Cataldi Robuffo Chiaverini Franchi
Tokyo, 5 November 2013

16. Experimental results
Experiments run at the Max Planck Institute of T¨bingen, Germany
u
case
a)
b)
c)
d)
additional
weight
Antonelli Cataldi Robuffo Chiaverini Franchi
weight
no
no
yes
yes
gain
λz
kvz
kγ,z
λxy
kv,xy
kγ,xy
kv,ϕθψ
kv,ϕθψ
krC
a/c
3
5.5
0
3
3
0
1
1
0
Tokyo, 5 November 2013
adaptive
no
yes
no
yes
b/d
3
5.5
1.5
3
3
1
1
1
.1

17. Experimental results
desired trajectory
1
η1,d [m]
0.5
0
−0.5
−1
−1.5
0
20
40
60
80
100
120
140
time [s]
Antonelli Cataldi Robuffo Chiaverini Franchi
Tokyo, 5 November 2013

18. Experimental results
Norm of the 3D position errors for the cases a) (green) and b) (blue)
(no weight)
0.35
η 1,d − η 1 [m]
0.3
0.25
0.2
0.15
0.1
0.05
0
0
20
40
60
80
time [s]
Antonelli Cataldi Robuffo Chiaverini Franchi
100
120
140
Tokyo, 5 November 2013

19. Experimental results
Norm of the 3D position errors for the cases c) (green) and d) (blue)
(weight)
0.35
η 1,d − η 1 [m]
0.3
0.25
0.2
0.15
0.1
0.05
0
0
20
40
60
80
time [s]
Antonelli Cataldi Robuffo Chiaverini Franchi
100
120
140
Tokyo, 5 November 2013

20. Experimental results
Roll (top) and pitch (bottom) angles for cases c) (green) and d) (blue)
ϕ [deg]
2
0
−2
−4
0
20
40
20
40
60
80
100
120
140
60
80
100
120
140
time [s]
θ [deg]
10
5
0
−5
0
time [s]
Antonelli Cataldi Robuffo Chiaverini Franchi
Tokyo, 5 November 2013

21. Experimental results
N [Nm] M [Nm] K [Nm]
Z [N]
Control forces for the cases c) (green) and d) (blue)
−14
−16
0
20
40
60
80
100
120
140
0
0
20
40
60
80
100
120
140
0.2
0
−0.2
−0.4
0
20
40
60
80
100
120
140
0.01
0
−0.01
−0.02
−0.03
0
20
40
60
80
100
120
140
time [s]
0.5
Antonelli Cataldi Robuffo Chiaverini Franchi
time [s]
time [s]
time [s]
Tokyo, 5 November 2013

22. Experimental results
ˆ
r C [m]
ˆ
γ xy [N]
γz [N]
ˆ
Time history of the parameters estimates for the case d). Top:
parameter γz , center: parameter γ xy , bottom: parameter r C .
−14
−16
−18
0
20
40
20
40
20
40
60
80
100
120
140
60
80
100
120
140
60
80
100
120
140
time [s]
1
0
−1
0
time [s]
0.05
0
−0.05
0
Antonelli Cataldi Robuffo Chiaverini Franchi
time [s]
Tokyo, 5 November 2013

23. Experimental validation of a new adaptive
control scheme for quadrotors MAVs
Gianluca Antonelli† , Elisabetta Cataldi† ,
Paolo Robuffo Giordano⊕ , Stefano Chiaverini† , Antonio Franchi≀
† University
of Cassino and Southern Lazio, Italy
http://webuser.unicas.it/lai/robotica
⊕ CNRS at IRISA and Inria Bretagne Atlantique, France
http://www.irisa.fr/lagadic
≀ Max Planck Institute for Biol. Cybernetics, Germany
http://www.kyb.mpg.de/research/dep/bu/hri/
IROS 2013
Antonelli Cataldi Robuffo Chiaverini Franchi
Tokyo, 5 November 2013