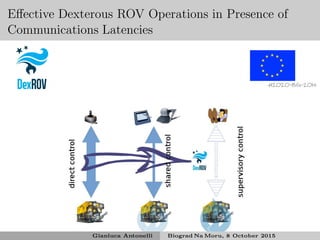
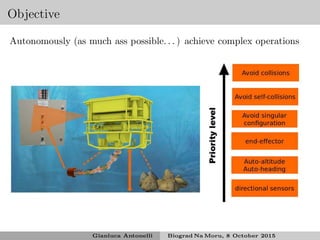
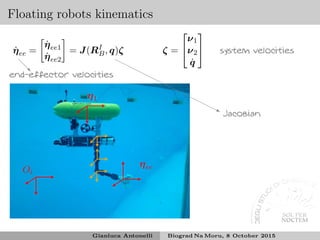
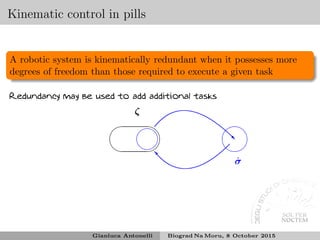
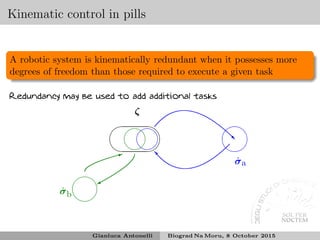
This document discusses underwater manipulation and robotic systems. It provides an overview of ISME, an Italian research unit, and some of its projects related to underwater robotics including MARIS, which aims to develop autonomous marine robotics for intervention tasks. It also discusses the state of the art in underwater manipulation, challenges including kinematics and dynamics when coordinating a vehicle and manipulator underwater. Various tasks that could be controlled are mentioned such as end effector position and orientation, joint limits, drag minimization, and obstacle avoidance.












![UVMS dynamics in matrix form
M(q)˙ζ + C(q, ζ)ζ + D(q, ζ)ζ + g(q, RI
B) = τ
formally equal to a ground-fixed industrial manipulator 1
however. . .
Model knowledge
Bandwidth of the sensor’s readings
Vehicle hovering control
Dynamic coupling between vehicle and manipulator
External disturbances (current)
Kinematic redundancy of the system
1
[Siciliano et al.(2009)Siciliano, Sciavicco, Villani, and Oriolo] [Fossen(2002)]
[Schjølberg and Fossen(1994)]
Gianluca Antonelli Biograd Na Moru, 8 October 2015](https://image.slidesharecdn.com/antonellibts2015-151008171257-lva1-app6891/85/Underwater-manipulation-18-320.jpg)
![Dynamics
Movement of vehicle and manipulator coupled
movement of the vehicle carrying the manipulator
law of conservation of momentum
Need to coordinate
at velocity level ⇒ kinematic control
at torque level ⇒ dynamic control 2
2
[McLain et al.(1996b)McLain, Rock, and Lee]
[McLain et al.(1996a)McLain, Rock, and Lee]
Gianluca Antonelli Biograd Na Moru, 8 October 2015](https://image.slidesharecdn.com/antonellibts2015-151008171257-lva1-app6891/85/Underwater-manipulation-19-320.jpg)
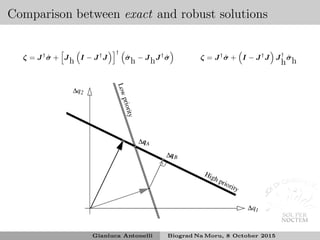
![A first solution
Assuming the vehicle in hovering is not the best strategy to e.e. fine
positioning3, better to kinematically compensate with the manipulator
3
[Hildebrandt et al.(2009)Hildebrandt, Christensen, Kerdels, Albiez, and Kirchner]
Gianluca Antonelli Biograd Na Moru, 8 October 2015](https://image.slidesharecdn.com/antonellibts2015-151008171257-lva1-app6891/85/Underwater-manipulation-20-320.jpg)

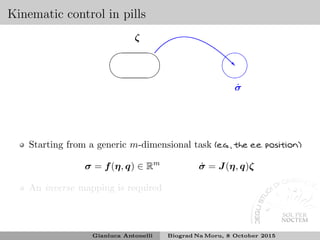
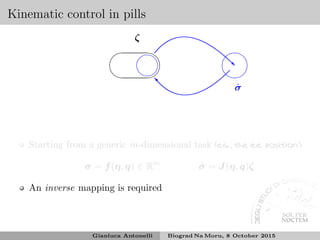



![Handling several tasks
Extended Jacobian4
Add additional (6 + n) − m constraints
h(η, q) = 0 with associated Jh
such that the problem is squared with
˙σ
0
=
J
Jh
ζ
4
[Chiaverini et al.(2008)Chiaverini, Oriolo, and Walker]
Gianluca Antonelli Biograd Na Moru, 8 October 2015](https://image.slidesharecdn.com/antonellibts2015-151008171257-lva1-app6891/85/Underwater-manipulation-30-320.jpg)


![Handling several tasks
Singularity robust task priority redundancy resolution 5
σh = h(η, q) with associated Jh
further projected on the the null space of the higher priority one
ζ = J†
˙σ + I − J†
J J†
h
˙σh
5
algorithmic singularities here. . . [Chiaverini(1997)]
Gianluca Antonelli Biograd Na Moru, 8 October 2015](https://image.slidesharecdn.com/antonellibts2015-151008171257-lva1-app6891/85/Underwater-manipulation-33-320.jpg)

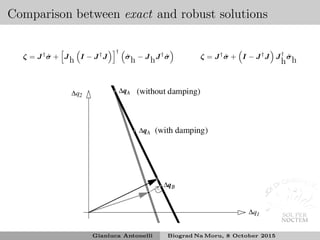
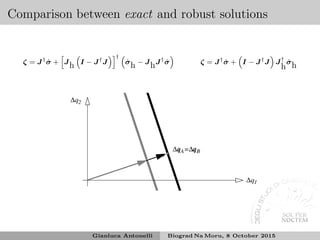
![Some issues
Kinematic singularities
Damped least square
Singular-value-decomposition-based filtering
Other kind of filtering
Algorithmic singularities
Two different-priority tasks are achievable alone but not together:
ranks of both J and Jh is full but not of
J
Jh
(still the
inversion of a singular matrix)
Set-based/inequality control 6
Task transition vs continuity/priority
6
[Escande et al.(2013)Escande, Mansard, and Wieber,
Simetti et al.(2013)Simetti, Casalino, Torelli, Sperind´e, and Turetta,
Antonelli et al.(2015)Antonelli, Moe, and Pettersen]
Gianluca Antonelli Biograd Na Moru, 8 October 2015](https://image.slidesharecdn.com/antonellibts2015-151008171257-lva1-app6891/85/Underwater-manipulation-39-320.jpg)



![Tasks to be controlled
Drag minimization, m = 1 7
h(q) = DT
(q, ζ)W D(q, ζ)
within a second order solution
˙ζ = J†
¨σ − ˙Jζ − k I − J†
J
∂h
∂η
∂h
∂q
+
∂h
∂ζ
7
[Sarkar and Podder(2001)]
Gianluca Antonelli Biograd Na Moru, 8 October 2015](https://image.slidesharecdn.com/antonellibts2015-151008171257-lva1-app6891/85/Underwater-manipulation-43-320.jpg)
![Tasks to be controlled
Manipulability/singularity, m = 1
h(q) = det JJT
(In 8 priorities dynamically swapped between singularity and e.e.)
joints
inhibited direction
singularity
singularity
setclose to
8
[Kim et al.(2002)Kim, Marani, Chung, and Yuh,
Casalino and Turetta(2003)] [Chiacchio et al.(1991)Chiacchio, Chiaverini, Sciavicco, and
Gianluca Antonelli Biograd Na Moru, 8 October 2015](https://image.slidesharecdn.com/antonellibts2015-151008171257-lva1-app6891/85/Underwater-manipulation-44-320.jpg)
![Tasks to be controlled
Restoring moments:
m = 3 keep close gravity-buoyancy of the overall system 9
m = 2 align gravity and buoyancy (SAUVIM is 4 tons) 10
fb
fg
τ 2
9
[Han and Chung(2008)]
10
[Marani et al.(2010)Marani, Choi, and Yuh]
Gianluca Antonelli Biograd Na Moru, 8 October 2015](https://image.slidesharecdn.com/antonellibts2015-151008171257-lva1-app6891/85/Underwater-manipulation-45-320.jpg)


![Tasks to be controlled
Visual servoing variables
Features in the image plane 11
11
[Mebarki et al.(2013)Mebarki, Lippiello, and Siciliano,
Mebarki and Lippiello(in press, 2014)]
Gianluca Antonelli Biograd Na Moru, 8 October 2015](https://image.slidesharecdn.com/antonellibts2015-151008171257-lva1-app6891/85/Underwater-manipulation-49-320.jpg)
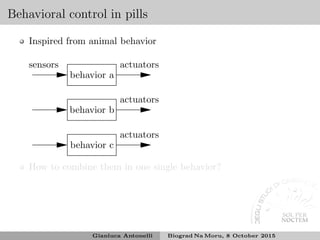

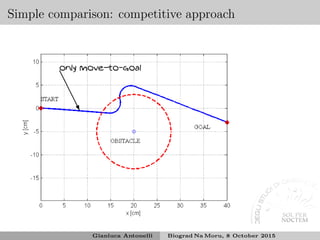
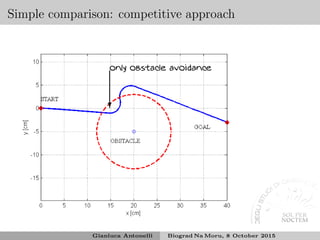
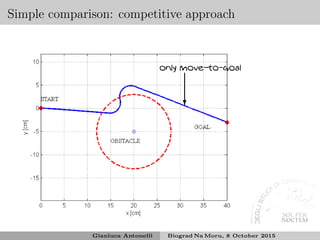
![Competitive behavioral control
Behaviors are in competitions and the higher priority can subsume the
lower ones12
sensors
behavior b
ζ2
behavior a
ζ1
behavior c
ζ3 ζd
12
[Brooks(1986)]
Gianluca Antonelli Biograd Na Moru, 8 October 2015](https://image.slidesharecdn.com/antonellibts2015-151008171257-lva1-app6891/85/Underwater-manipulation-53-320.jpg)
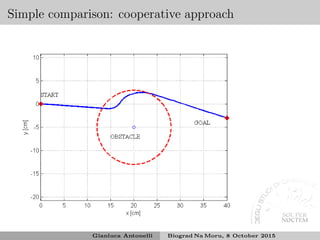
![Cooperative behavioral control
Behaviors cooperate and the priority is embedded in the gains13
sensors
behavior b
ζ2
α2
behavior a
ζ1
supervisor
α1
behavior c
ζ3
α3
ζd
13
[Arkin(1989)]
Gianluca Antonelli Biograd Na Moru, 8 October 2015](https://image.slidesharecdn.com/antonellibts2015-151008171257-lva1-app6891/85/Underwater-manipulation-54-320.jpg)
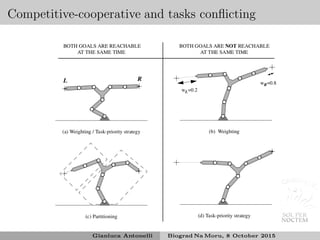








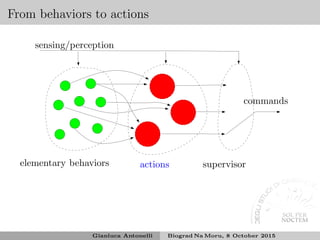

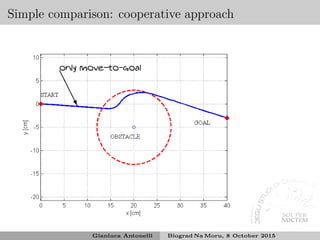
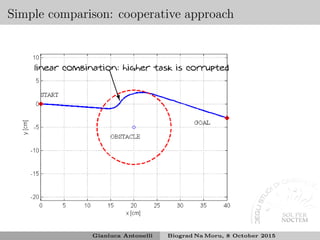
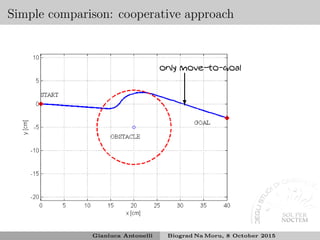
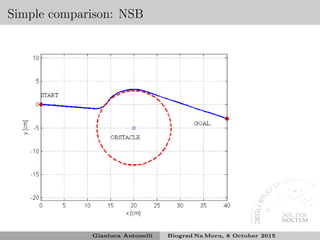
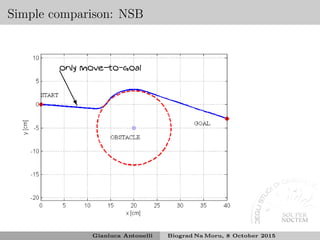
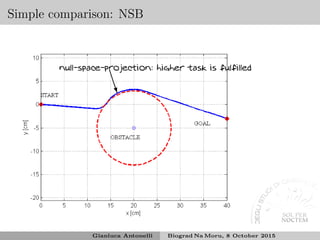
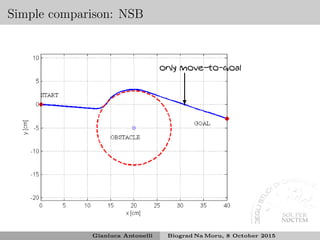



![Stability analysis
Lyapunov function14
V (˜σ) = 1
2 ˜σT
˜σ > 0 where ˜σ = ˜σT
a ˜σT
b ˜σT
c
T
˙V = −˜σT
Ja
Jb
Jc
v = −˜σT
M ˜σ = −˜σT
Λa Oma,mb Oma,mc
JbJ†
aΛa JbNaJ†
bΛb JbNJ†
cΛc
JcJ†
aΛa JcNaJ†
bΛb JcNJ†
cΛc
˜σ
˙V < 0 depending on the mutual relationships among the Jacobians
14
[Antonelli(2009)]
Gianluca Antonelli Biograd Na Moru, 8 October 2015](https://image.slidesharecdn.com/antonellibts2015-151008171257-lva1-app6891/85/Underwater-manipulation-81-320.jpg)
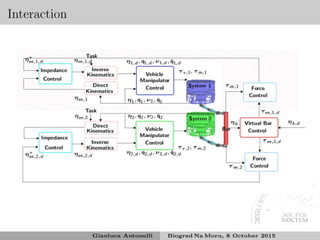


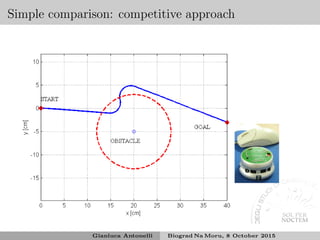
![Simulations and experiments within TRIDENT
[Simetti et al.(2013)Simetti, Casalino, Torelli, Sperind´e, and Turetta]
Gianluca Antonelli Biograd Na Moru, 8 October 2015](https://image.slidesharecdn.com/antonellibts2015-151008171257-lva1-app6891/85/Underwater-manipulation-86-320.jpg)









