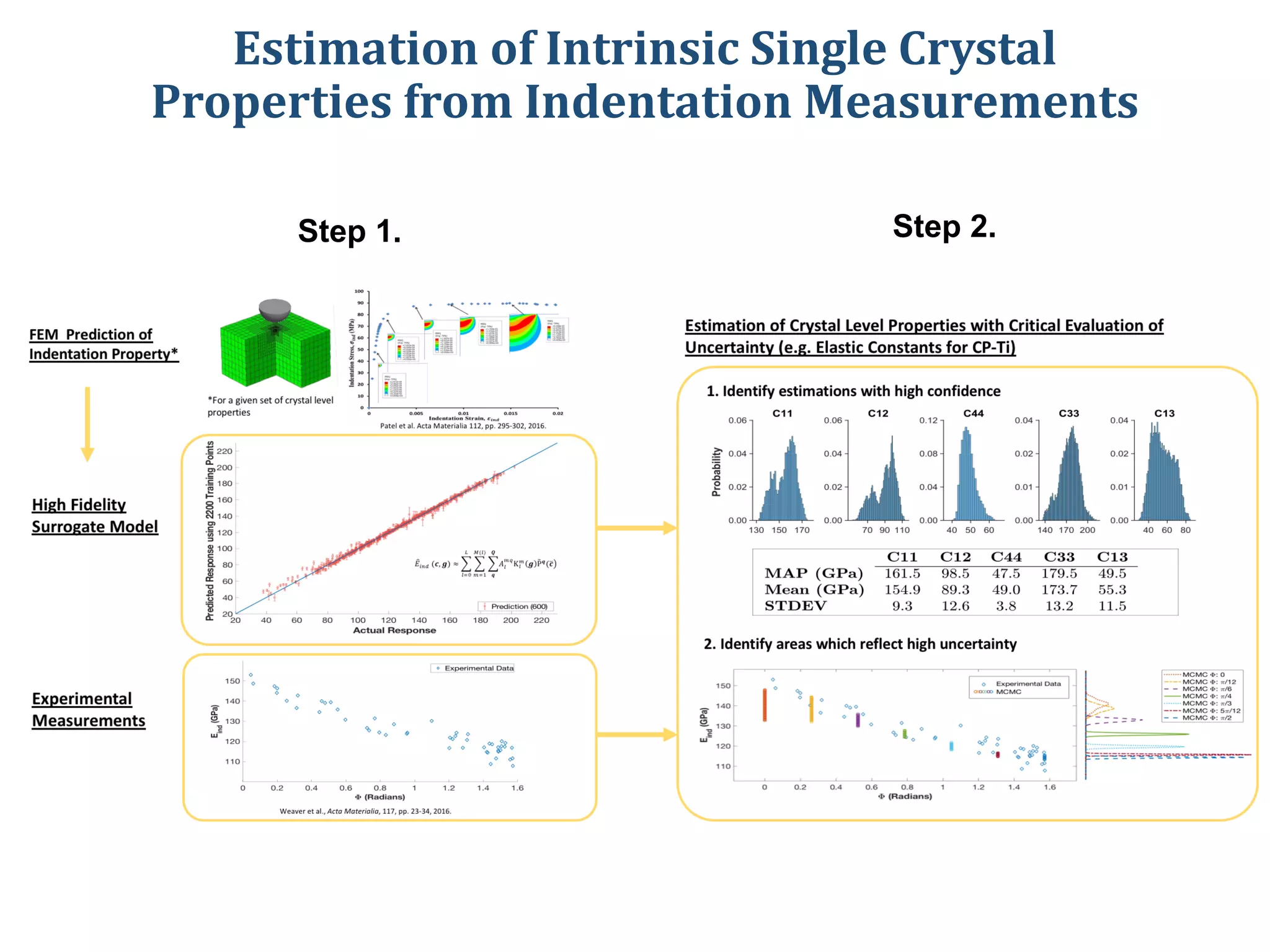
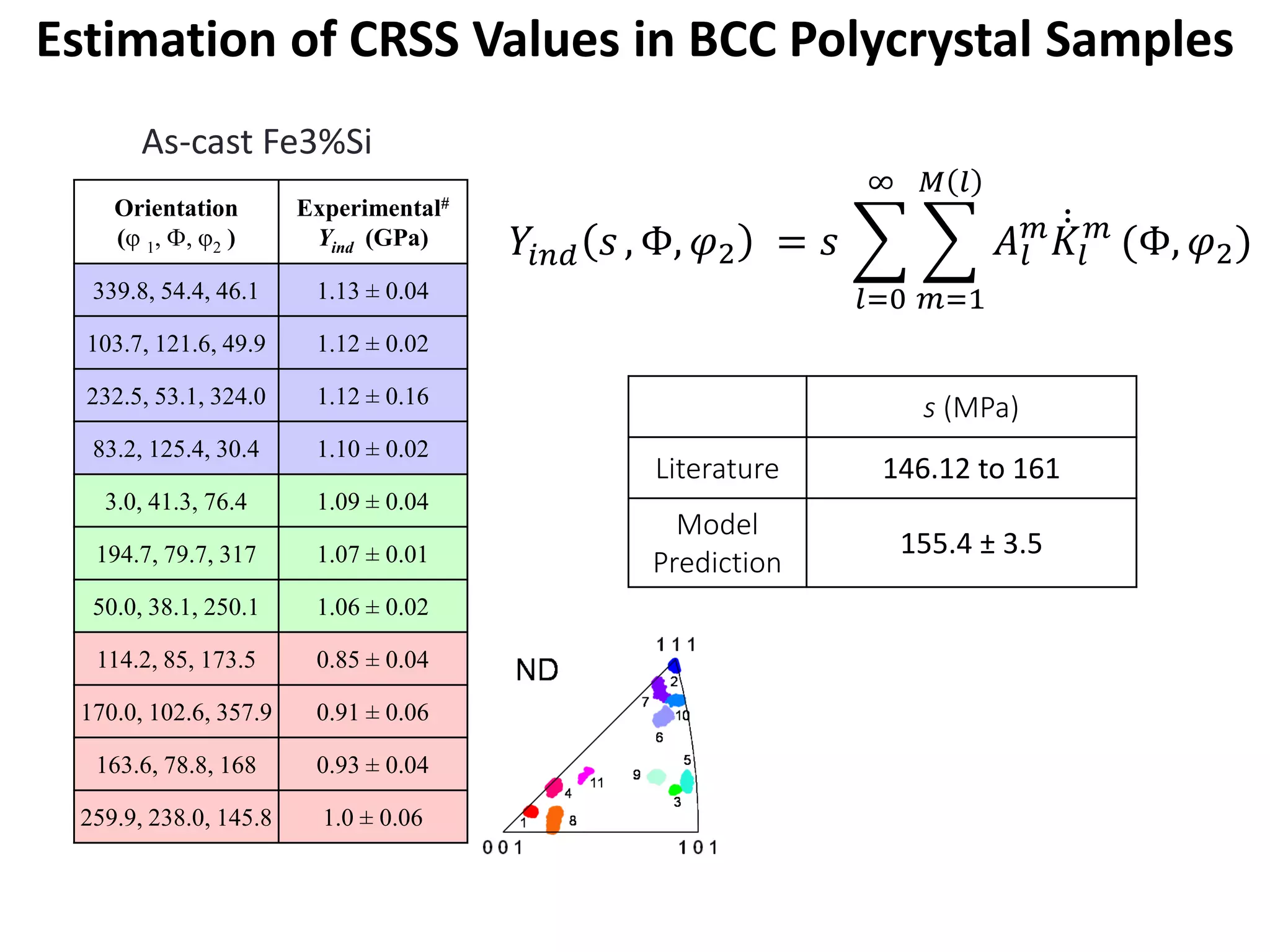
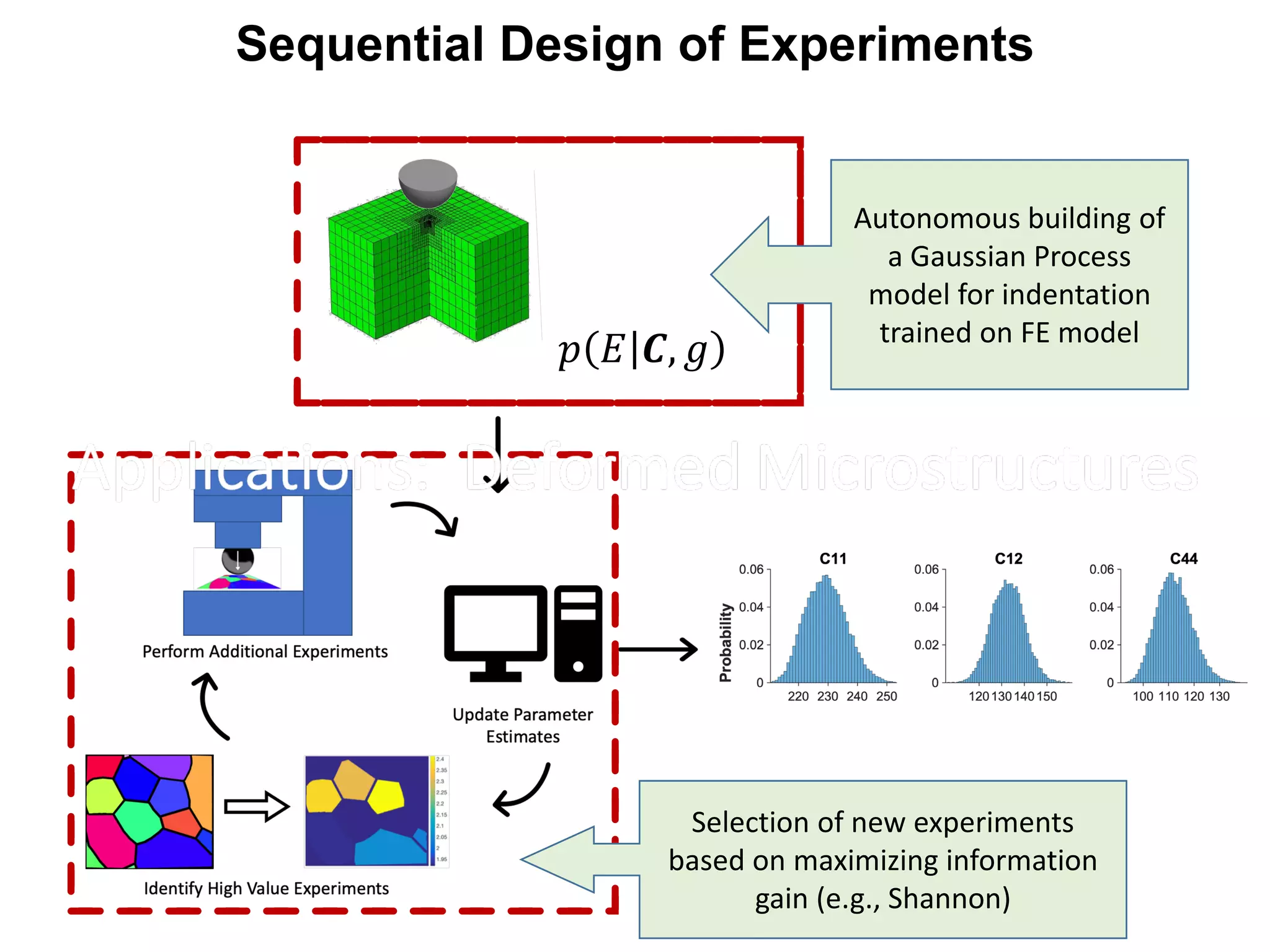
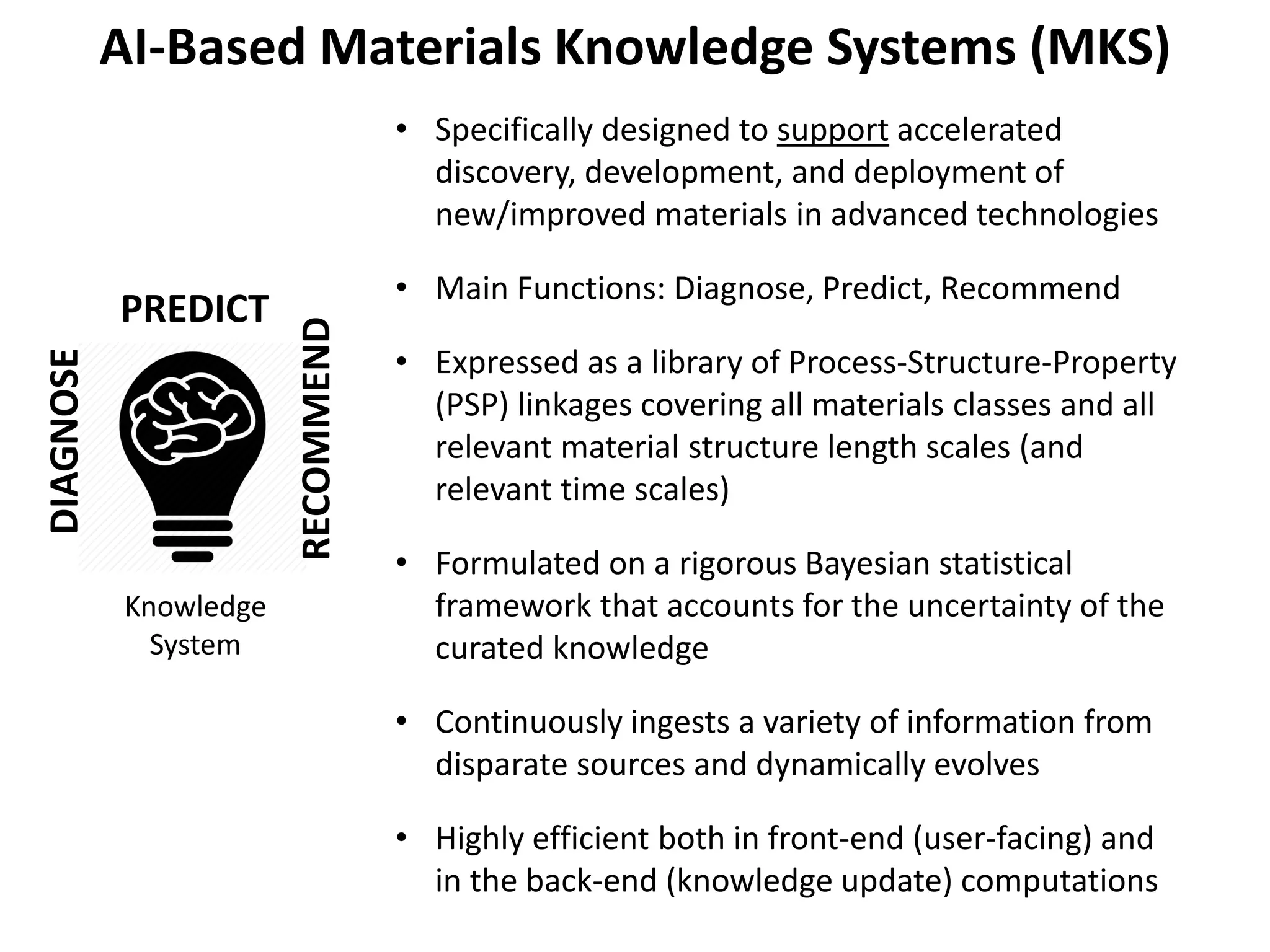
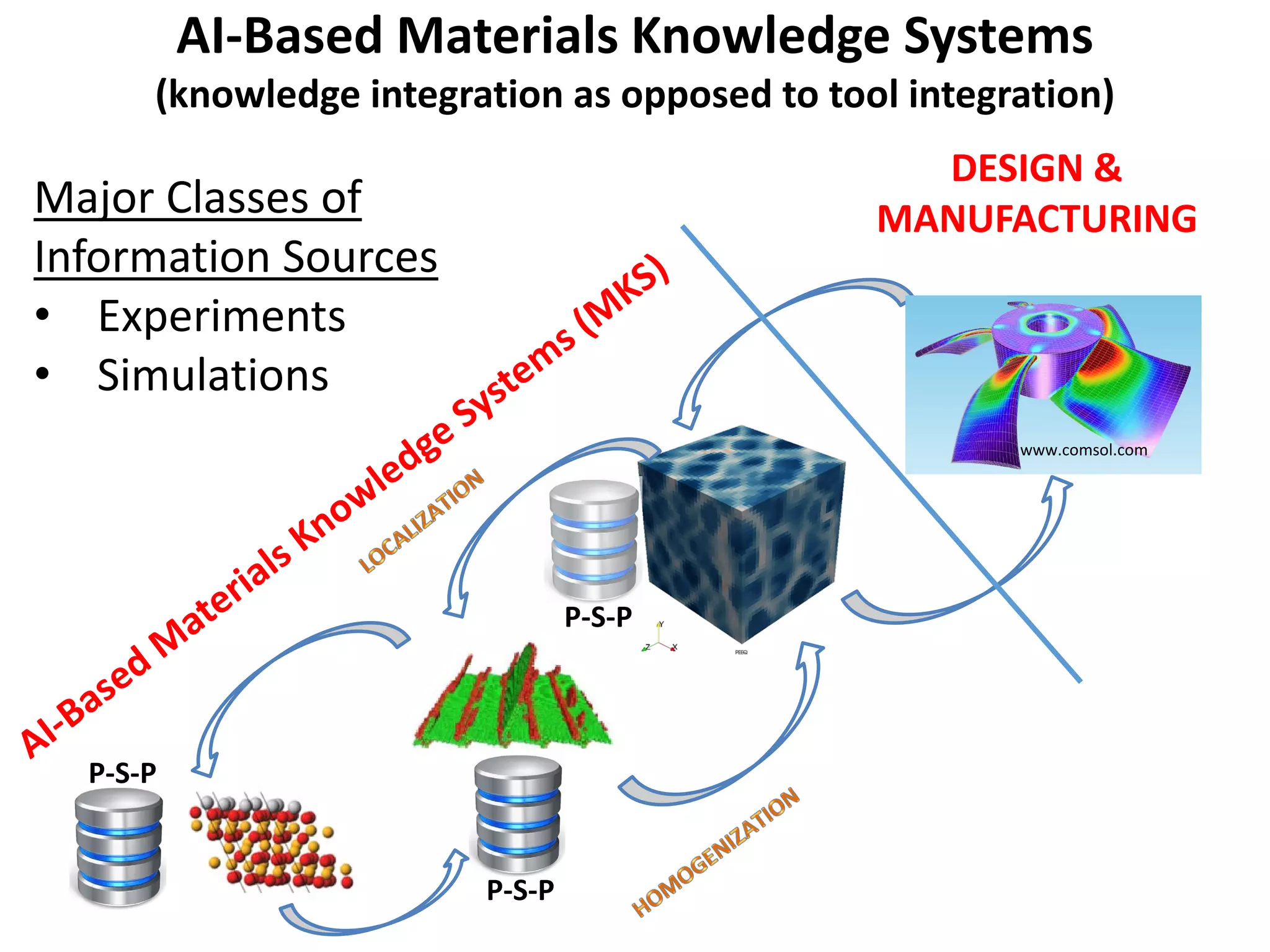
- The document describes a machine learning framework for developing artificial intelligence-based materials knowledge systems (MKS) to support accelerated materials discovery and development.
- The MKS would have main functions of diagnosing materials problems, predicting materials behaviors, and recommending materials selections or process adjustments.
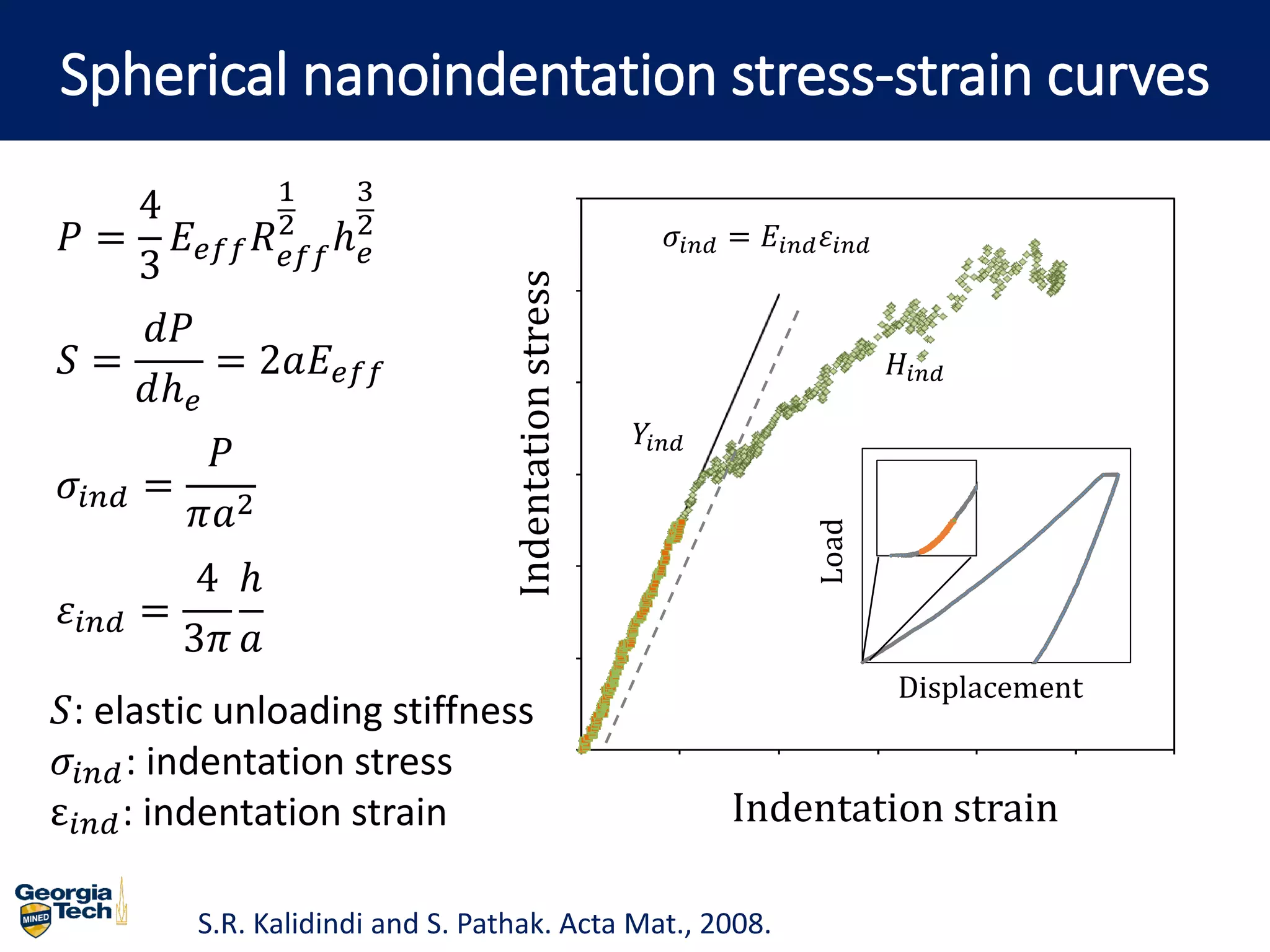
- It would utilize a Bayesian statistical approach to curate process-structure-property linkages for all materials classes and length scales, accounting for uncertainty in the knowledge, and allow continuous updates from new information sources.
Machine Learning for Molecules: Lessons and Challenges of Data-Centric ChemistryIchigaku Takigawa
Perspectives on Artificial Intelligence and Machine Learning in Materials Science
February 4, 2022. – February 6, 2022.
https://joint.imi.kyushu-u.ac.jp/post-2698/
Current approaches to exploring materials and manufacturing (or processing) design spaces in pursuit of new/improved engineered structural materials continue to rely heavily on extensive experimentation, which typically demand inordinate investments in both time and effort. Although tremendous progress has been made in the development and validation of a wide range of simulation toolsets capturing the multiscale phenomena controlling the material properties and performance characteristics of interest to advanced technologies, their systematic insertion into the materials innovation efforts has encountered several hurdles. The most common of these are related to (i) the lack of a generalized (applicable to a wide variety of materials classes and phenomena) mathematical framework that allows objective extraction and synergistic integration of the high value materials knowledge (defined from the perspective of producing reliable process-structure-property (PSP) linkages) from all available datasets (including a variety of multiscale experiments and simulations), while accounting for the inherent uncertainty associated with each dataset, (ii) the lack of formal approaches that identify objectively where to invest the next effort (could be a new experiment or a new simulation) for maximizing the likelihood of success (i.e., meeting or exceeding the designer-specified combinations of materials properties) at any step of the innovation effort, and (iii) the lack of experimental techniques that are specifically designed to provide the quality and quantity of information needed to calibrate the large number of material parameters present in most multiscale materials models. This talk will describe ongoing efforts in my research group aimed at addressing the gaps identified above.
Machine Learning for Molecules: Lessons and Challenges of Data-Centric ChemistryIchigaku Takigawa
Perspectives on Artificial Intelligence and Machine Learning in Materials Science
February 4, 2022. – February 6, 2022.
https://joint.imi.kyushu-u.ac.jp/post-2698/
Current approaches to exploring materials and manufacturing (or processing) design spaces in pursuit of new/improved engineered structural materials continue to rely heavily on extensive experimentation, which typically demand inordinate investments in both time and effort. Although tremendous progress has been made in the development and validation of a wide range of simulation toolsets capturing the multiscale phenomena controlling the material properties and performance characteristics of interest to advanced technologies, their systematic insertion into the materials innovation efforts has encountered several hurdles. The most common of these are related to (i) the lack of a generalized (applicable to a wide variety of materials classes and phenomena) mathematical framework that allows objective extraction and synergistic integration of the high value materials knowledge (defined from the perspective of producing reliable process-structure-property (PSP) linkages) from all available datasets (including a variety of multiscale experiments and simulations), while accounting for the inherent uncertainty associated with each dataset, (ii) the lack of formal approaches that identify objectively where to invest the next effort (could be a new experiment or a new simulation) for maximizing the likelihood of success (i.e., meeting or exceeding the designer-specified combinations of materials properties) at any step of the innovation effort, and (iii) the lack of experimental techniques that are specifically designed to provide the quality and quantity of information needed to calibrate the large number of material parameters present in most multiscale materials models. This talk will describe ongoing efforts in my research group aimed at addressing the gaps identified above.
발표자: 송환준(KAIST 박사과정)
발표일: 2018.8.
(Parallel Clustering Algorithm Optimization for Large-Scale Data Analytics)
Clustering은 데이터 분석에 가장 널리 쓰이는 방법 중 하나로 주어진 데이터를 유사성에 기초하여 여러 개의 그룹으로 나누는 작업이다. 하지만 Clustering 방법의 높은 계산 복잡도 때문에 대용량 데이터 분석에는 잘 사용되지 못하고 있다. 최근 이 높은 복잡도 문제를 해결하기 위해 많은 연구가 Hadoop, Spark와 같은 분산 컴퓨팅 방식을 적용하고 있지만 기존 Clustering 알고리즘을 분산 환경에 최적화시키는 것은 쉽지 않다. 특히, 효율성을 높이기 위해 정확성을 손실하는 문제 그리고 여러 작업자들 간의 부하 불균형 문제는 알고리즘을 분산처리 할 때 발생하는 대표적인 문제이다. 본 세미나에서는 대표적 Clustering 알고리즘인 DBSCAN을 분산처리 할 때 발생하는 여러 도전 과제에 초점을 맞추고 이를 해결 할 수 있는 새로운 해결책을 제시한다. 실제로 이 방법은 최신 연구의 방법과 비교하여 정확도 손실 없이 최대 180배까지 알고리즘의 성능을 향상시켰다.
본 세미나는 SIGMOD 2018에서 발표한 다음 논문에 대한 내용이다.
Song, H. and Lee, J., "RP-DBSCAN: A Superfast Parallel DBSCAN Algorithm Based on Random Partitioning," In Proc. 2018 ACM Int'l Conf. on Management of Data (SIGMOD), Houston, Texas, pp. 1173 ~ 1187, June 2018
1. Background
- Concept of Clustering
- Concept of Distributed Processing (MapReduce)
- Clustering Algorithms (Focus on DBSCAN)
2. Challenges of Parallel Clustering
- Parallelization of Clustering Algorithm (Focus on DBSCAN)
- Existing Work
- Challenges
3. Our Approach
- Key Idea and Key Contribution
- Overview of Random Partitioning-DBSCAN
4. Experimental Results
5. Conclusions
Data Science Solutions by Materials Scientists: The Early Case StudiesTony Fast
Improvements in algorithms, technology, and computation are directly impacting the landscape of information use in materials science. The 3 V’s of Big Data (volume, velocity, and variety) are becoming evermore apparent within all sectors of the field. Novel approaches will be required to confront the emerging data deluge and extract the richest knowledge from simulated and empirical information in complex evolving 3-D spaces. Microstructure Informatics (μInformatics) is an emerging suite of signal processing techniques, advanced statistical tools, and data science methods tailored specifically for this new frontier. μInformatics curates and transforms large collections of materials science information using efficient workflows to extract knowledge of bi-directional structure-property/processing connections for most material classes.
In this talk, a few early case studies in data-driven methods to solve materials science problems will be explored. Emerging spatial statistics tools will be explored that enable an objective comparison of static and evolving 3-D material volumes from molecular dynamics simulation, micro-CT, and Scanning Electron Microscopy. Also, the statistics will provide a foundation to create improved bottom-up homogenization relationships in fuel cell materials. Lastly, applications of the Materials Knowledge System, a data-driven meta-model to create top-down localization relationships will be explored for phase field model and finite element model information.
In this deck from the DOE CSGF Program Review meeting, Nicholas Frontiere from the University of Chicago presents: HACC - Fitting the Universe Inside a Supercomputer.
"In response to the plethora of data from current and future large-scale structure surveys of the universe, sophisticated simulations are required to obtain commensurate theoretical predictions. We have developed the Hardware/Hybrid Accelerated Cosmology Code (HACC), capable of sustained performance on powerful and architecturally diverse supercomputers to address this numerical challenge. We will investigate the numerical methods utilized to solve a problem that evolves trillions of particles, with a dynamic range of a million to one."
Watch the video: https://wp.me/p3RLHQ-i4l
Learn more: https://www.krellinst.org/csgf/conf/2017/
Sign up for our insideHPC Newsletter: http://insidehpc.com/newsletter
Ijricit 01-002 enhanced replica detection in short time for large data setsIjripublishers Ijri
Similarity check of real world entities is a necessary factor in these days which is named as Data Replica Detection.
Time is an critical factor today in tracking Data Replica Detection for large data sets, without having impact over quality
of Dataset. In this we primarily introduce two Data Replica Detection algorithms , where in these contribute enhanced
procedural standards in finding Data Replication at limited execution periods.This contribute better improvised state
of time than conventional techniques . We propose two Data Replica Detection algorithms namely progressive sorted
neighborhood method (PSNM), which performs best on small and almost clean datasets, and progressive blocking (PB),
which performs best on large and very grimy datasets. Both enhance the efficiency of duplicate detection even on very
large datasets.
In this deck from the HPC User Forum at Argonne, Andrew Siegel from Argonne presents: ECP Application Development.
"The Exascale Computing Project is accelerating delivery of a capable exascale computing ecosystem for breakthroughs in scientific discovery, energy assurance, economic competitiveness, and national security. ECP is chartered with accelerating delivery of a capable exascale computing ecosystem to provide breakthrough modeling and simulation solutions to address the most critical challenges in scientific discovery, energy assurance, economic competitiveness, and national security. This role goes far beyond the limited scope of a physical computing system. ECP’s work encompasses the development of an entire exascale ecosystem: applications, system software, hardware technologies and architectures, along with critical workforce development."
Watch the video: https://wp.me/p3RLHQ-kSL
Learn more: https://www.exascaleproject.org
and
http://hpcuserforum.com
Sign up for our insideHPC Newsletter: http://insidehpc.com/newsletter
Computational Discovery of Two-Dimensional Materials, Evaluation of Force-Fie...KAMAL CHOUDHARY
JARVIS (Joint Automated Repository for Various Integrated Simulations) is a repository designed to automate materials discovery using classical force-field, density functional theory, machine learning calculations and experiments.
The Force-field section of JARVIS (JARVIS-FF) consists of thousands of automated LAMMPS based force-field calculations on DFT geometries. Some of the properties included in JARVIS-FF are energetics, elastic constants, surface energies, defect formations energies and phonon frequencies of materials.
The Density functional theory section of JARVIS (JARVIS-DFT) consists of thousands of VASP based calculations for 3D-bulk, single layer (2D), nanowire (1D) and molecular (0D) systems. Most of the calculations are carried out with optB88vDW functional. JARVIS-DFT includes materials data such as: energetics, diffraction pattern, radial distribution function, band-structure, density of states, carrier effective mass, temperature and carrier concentration dependent thermoelectric properties, elastic constants and gamma-point phonons.
The Machine-learning section of JARVIS (JARVIS-ML) consists of machine learning prediction tools, trained on JARVIS-DFT data. Some of the ML-predictions focus on energetics, heat of formation, GGA/METAGGA bandgaps, bulk and shear modulus. The ML webpage is visible to NIST employees only right now, but will be available publicly soon.
Welcome to WIPAC Monthly the magazine brought to you by the LinkedIn Group Water Industry Process Automation & Control.
In this month's edition, along with this month's industry news to celebrate the 13 years since the group was created we have articles including
A case study of the used of Advanced Process Control at the Wastewater Treatment works at Lleida in Spain
A look back on an article on smart wastewater networks in order to see how the industry has measured up in the interim around the adoption of Digital Transformation in the Water Industry.
Immunizing Image Classifiers Against Localized Adversary Attacksgerogepatton
This paper addresses the vulnerability of deep learning models, particularly convolutional neural networks
(CNN)s, to adversarial attacks and presents a proactive training technique designed to counter them. We
introduce a novel volumization algorithm, which transforms 2D images into 3D volumetric representations.
When combined with 3D convolution and deep curriculum learning optimization (CLO), itsignificantly improves
the immunity of models against localized universal attacks by up to 40%. We evaluate our proposed approach
using contemporary CNN architectures and the modified Canadian Institute for Advanced Research (CIFAR-10
and CIFAR-100) and ImageNet Large Scale Visual Recognition Challenge (ILSVRC12) datasets, showcasing
accuracy improvements over previous techniques. The results indicate that the combination of the volumetric
input and curriculum learning holds significant promise for mitigating adversarial attacks without necessitating
adversary training.
Saudi Arabia stands as a titan in the global energy landscape, renowned for its abundant oil and gas resources. It's the largest exporter of petroleum and holds some of the world's most significant reserves. Let's delve into the top 10 oil and gas projects shaping Saudi Arabia's energy future in 2024.
Cosmetic shop management system project report.pdfKamal Acharya
Buying new cosmetic products is difficult. It can even be scary for those who have sensitive skin and are prone to skin trouble. The information needed to alleviate this problem is on the back of each product, but it's thought to interpret those ingredient lists unless you have a background in chemistry.
Instead of buying and hoping for the best, we can use data science to help us predict which products may be good fits for us. It includes various function programs to do the above mentioned tasks.
Data file handling has been effectively used in the program.
The automated cosmetic shop management system should deal with the automation of general workflow and administration process of the shop. The main processes of the system focus on customer's request where the system is able to search the most appropriate products and deliver it to the customers. It should help the employees to quickly identify the list of cosmetic product that have reached the minimum quantity and also keep a track of expired date for each cosmetic product. It should help the employees to find the rack number in which the product is placed.It is also Faster and more efficient way.
Water scarcity is the lack of fresh water resources to meet the standard water demand. There are two type of water scarcity. One is physical. The other is economic water scarcity.
CFD Simulation of By-pass Flow in a HRSG module by R&R Consult.pptxR&R Consult
CFD analysis is incredibly effective at solving mysteries and improving the performance of complex systems!
Here's a great example: At a large natural gas-fired power plant, where they use waste heat to generate steam and energy, they were puzzled that their boiler wasn't producing as much steam as expected.
R&R and Tetra Engineering Group Inc. were asked to solve the issue with reduced steam production.
An inspection had shown that a significant amount of hot flue gas was bypassing the boiler tubes, where the heat was supposed to be transferred.
R&R Consult conducted a CFD analysis, which revealed that 6.3% of the flue gas was bypassing the boiler tubes without transferring heat. The analysis also showed that the flue gas was instead being directed along the sides of the boiler and between the modules that were supposed to capture the heat. This was the cause of the reduced performance.
Based on our results, Tetra Engineering installed covering plates to reduce the bypass flow. This improved the boiler's performance and increased electricity production.
It is always satisfying when we can help solve complex challenges like this. Do your systems also need a check-up or optimization? Give us a call!
Work done in cooperation with James Malloy and David Moelling from Tetra Engineering.
More examples of our work https://www.r-r-consult.dk/en/cases-en/
Student information management system project report ii.pdfKamal Acharya
Our project explains about the student management. This project mainly explains the various actions related to student details. This project shows some ease in adding, editing and deleting the student details. It also provides a less time consuming process for viewing, adding, editing and deleting the marks of the students.
Runway Orientation Based on the Wind Rose Diagram.pptx
A Machine Learning Framework for Materials Knowledge Systems
1. A Machine Learning Framework for Materials
Knowledge Systems
Surya R. Kalidindi
Funding: DoD, NIST
2. AI-Based Materials Knowledge Systems (MKS)
Knowledge
System
PREDICT
DIAGNOSE
RECOMMEND
• Specifically designed to support accelerated
discovery, development, and deployment of
new/improved materials in advanced technologies
• Main Functions: Diagnose, Predict, Recommend
• Expressed as a library of Process-Structure-Property
(PSP) linkages covering all materials classes and all
relevant material structure length scales (and
relevant time scales)
• Formulated on a rigorous Bayesian statistical
framework that accounts for the uncertainty of the
curated knowledge
• Continuously ingests a variety of information from
disparate sources and dynamically evolves
• Highly efficient both in front-end (user-facing) and
in the back-end (knowledge update) computations
3. Process
• Thermo-
mechanical (T(t),
L(t), σ(t), ̇𝑐𝑐(t), … )
• Placement of
Specific Defects
(e.g., grain/phase
boundaries,
𝑔𝑔, ∆𝑔𝑔, 𝑛𝑛)
• Placement of
chemical species
(𝑐𝑐𝑖𝑖, 𝑉𝑉, 𝑝𝑝, 𝒙𝒙𝑛𝑛, … )
Structure
• Microstructure
• Dislocation/defect
structure
• Interface atomic
structure
• Atomic structure
with defects,
disorder, etc.
• Electron density
field
Property
• Young’s Modulus
• Yield Strength
• Fatigue Strength
• Conductivity
• Permeability
• Critical Resolved
Shear Strength
• Grain Boundary
Energy
• Vacancy Formation
Energy
PSP Linkages Over a Hierarchy of Material Structure Scales
• Process and Property variables have rigorous mathematical definitions
• Critical Need: A framework for high-value low-dimensional representations of the
material structure (minimal information loss with maximum recoverability) that is
broadly applicable to various material classes at different length scales.
4. AI-Based Materials Knowledge Systems
(knowledge integration as opposed to tool integration)
www.comsol.com
DESIGN &
MANUFACTURING
P-S-P
P-S-P
P-S-P
Major Classes of
Information Sources
• Experiments
• Simulations
5. Stochastic Framework for MKS
• Property: 𝑃𝑃 ∈ ℛ; 𝑝𝑝 𝑃𝑃 = 𝒩𝒩 𝑃𝑃 �𝑃𝑃, 𝜎𝜎𝑝𝑝
2
• Material (Hierarchical) Structure: 𝝁𝝁 ∈ 𝓜𝓜; 𝑝𝑝 𝝁𝝁 = 𝒩𝒩 𝝁𝝁 �𝝁𝝁, 𝜮𝜮𝝁𝝁
• Process: 𝓟𝓟 ∈ ℛ𝑛𝑛
; 𝑝𝑝 𝓟𝓟 = 𝒩𝒩 𝓟𝓟 �𝓟𝓟, 𝜮𝜮𝓟𝓟
• Governing Physics: expressed as field (differential) equations and material
constitutive laws or equivalently as Green’s functions
𝝋𝝋 ∈ 𝚽𝚽; 𝑝𝑝 𝝋𝝋 = 𝒩𝒩 𝝋𝝋 �𝝋𝝋, 𝜮𝜮𝝋𝝋
• Physics-Based Simulations: 𝑝𝑝 𝑃𝑃 𝝁𝝁, 𝝋𝝋, 𝜮𝜮𝝁𝝁 , 𝜮𝜮𝝋𝝋 and 𝑝𝑝 𝝁𝝁 𝓟𝓟, 𝝋𝝋, 𝜮𝜮𝓟𝓟 , 𝜮𝜮𝝋𝝋 -
machine learning has opened new avenues for sampling these distributions
within practical computational budgets
• Physical Experiments (typically small datasets): 𝑝𝑝 𝑃𝑃 𝝁𝝁, 𝜮𝜮𝝁𝝁 , 𝝋𝝋∗ and
𝑝𝑝 𝝁𝝁 𝓟𝓟, 𝜮𝜮𝓟𝓟 , 𝝋𝝋∗
; 𝝋𝝋∗
= undetermined governing physics
6. Bayesian Update of Governing Physics
(a formal framework for uncovering new physics)
𝑝𝑝 𝝋𝝋 𝑬𝑬, 𝜮𝜮𝑬𝑬 ∝ 𝑝𝑝 𝑬𝑬 𝝋𝝋, 𝜮𝜮𝑬𝑬 𝑝𝑝 𝝋𝝋
Physics-Based Simulations
Build Gaussian Process models trained
to simulation datasets produced by
executing physics-based models by
adaptive sampling of input domain for
maximizing fidelity of extracted GP.
Process-Structure: 𝑝𝑝 𝝁𝝁 𝓟𝓟, 𝝋𝝋, 𝜮𝜮𝓟𝓟 , 𝜮𝜮𝝋𝝋
Structure-Property: 𝑝𝑝 𝑃𝑃 𝝁𝝁, 𝝋𝝋, 𝜮𝜮𝝁𝝁 , 𝜮𝜮𝝋𝝋
Sequential Design of Physical
Experiments
Decide on the next experiment
that is likely to produce the
largest information gain in
updating the governing physics.
Foundational framework for Materials Knowledge Systems: Diagnose, Predict, Recommend
7. Structure Quantification: n-Point Spatial Correlations
• Spatial correlations capture all of the salient measures of the microstructure
• Allow efficient computations using discrete Fourier transforms (DFTs)
𝑓𝑓𝒓𝒓
𝑛𝑛𝑛𝑛
=
1
𝑆𝑆𝒓𝒓
1
𝐽𝐽
�
𝒔𝒔
�
𝑗𝑗=1
𝐽𝐽
(𝑗𝑗)
𝑚𝑚𝒔𝒔
𝑛𝑛 (𝑗𝑗)
𝑚𝑚𝒔𝒔+𝒓𝒓
𝑝𝑝
𝑓𝑓𝑟𝑟
ℎℎ′
=
# 𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇 𝑆𝑆𝑆𝑆𝑆𝑆𝑆𝑆𝑆𝑆𝑆𝑆𝑆𝑆𝑆𝑆𝑆𝑆𝑆𝑆
# 𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇𝑇 𝐴𝐴𝐴𝐴𝐴𝐴 𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴
%50
%0
Complete Set of 𝑓𝑓𝑟𝑟
ℎℎ′
for
all possible 𝑟𝑟
S. R. Kalidindi, “Hierarchical Materials Informatics”, Butterworth Heinemann, 2015.
9. a c db
Input:
atomic coordinates
Lattice Dimensions
(From atomistic file
formats)
Generate grid
representation of the
Molecular Structure
Compute the pore
region that can be
accessed by a probe
molecule
Compute pore
characteristics:
Accessible Volume,
PLD, LCD,
Accessible Paths,
Tortuosity
AtomMKS: Quantification of Atomic Structures
Define features of interest in a rigorous statistical framework → Feature Engineering
10. Low-Dimensional Representations of material structure
distributions Using PCA
𝑓𝑓𝑟𝑟
(𝑗𝑗)
≈ �
𝑘𝑘=1
�𝑅𝑅
𝛼𝛼𝑘𝑘
(𝑗𝑗)
𝜑𝜑𝑘𝑘𝑘𝑘 + ̅𝑓𝑓𝑟𝑟
Microstructure (µ) = (7.95, 0.46, 0.78)
S. R. Kalidindi, “Hierarchical Materials Informatics”, Butterworth Heinemann, 2015.
11. 11
Templated Workflows for Extracting PSP Linkages
PyMKS (www.pymks.org) ~ 4000 downloads in last 12 months
https://github.com/ahmetcecen/MATLAB-Spatial-Correlation-Toolbox
12. MKS Homogenization for Multiphase Plasticity
• MKS Homogenization Framework
• Effective Yield Strength
• Partitioning of the imposed strains among
the microscale constituents
• Single database for a broad range of
contrasts
Isotropic perfectly-plastic
YS2:YS1 = 2:1 … 10:1
Latypov and Kalidindi, Journal of Computational Physics, 346, pp. 242–261, 2017
Latypov et al., Computer Methods in Applied Mechanics and Engineering, 346, pp. 180-196, 2019
13. Prediction of Composite Stress-Strain Responses
FEM
MKS
User-specified
hardening laws
for each phase
̇𝑔𝑔𝛼𝛼 = ℎ𝛼𝛼 𝑔𝑔 ̇𝜖𝜖𝛼𝛼
̇𝑔𝑔𝛽𝛽 = ℎ𝛽𝛽(𝑔𝑔) ̇𝜖𝜖𝛽𝛽
3-D Microstructure
Inputs
CPU Time MKS: 0.5 s
FEM: up to ~24 hrs
Outputs
14. Correlation of Images to Properties
Optical Images of Steel Samples
500 550 600 650 700 750 800 850 900 950
Predicted Value
500
550
600
650
700
750
800
850
900
950
TrueYieldStrValue
𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴 𝑒𝑒𝑒𝑒𝑒𝑒𝑒𝑒𝑒𝑒 = 2.5%
Image Segmentation Reduced-Order Microstructure
Representation
Reduced-Order Model
15. Grain 1
Material: Ni (FCC)
Properties of Interest:
● Grain Boundary
Energy
● Mobility
41 types of sigma-3
Grain Boundaries and
associated property
values provided.
Grain boundary atoms
identified using Common
Neighbour Analysis. Atoms
other than FCC constitute grain
boundary.
atomMKS: Application to Grain Boundary Structures
Collaboration with Prof. Fadi Abdeljawad, Clemson University
16. RMS Error: 0.037 J/m2
RMS error: 96.39 m/(s GPa)
Grain Boundary MobilityGrain Boundary Energy
Training Data: Red
Test Data: Green
atomMKS: Reduced-order Models Using Ridge-
Regression on PC Scores
17. • 45 x 45 x 45 Microstructure. Each color
represents a distinct crystal lattice orientation
randomly selected from cubic FZ.
• FEM prediction: 3 minutes with 16
processors on a supercomputer
• MKS prediction: 30 seconds with only 1
processor on a standard desktop computer
Stress Fields in Polycrystals
Yabansu and Kalidindi, Acta Materialia, 94, pp. 26–35, 2015
18. For a 43X43X43 RVE
the FEM analysis
required 15 hours on
a one 2.4 GHz AMD
processor node in the
Georgia Tech super
computer cluster,
while the MKS
predictions were
obtained in 306.5
seconds on the same
resource.
Plastic Strain Rates in Two-Phase Composites
Montes De Oca Zapiain et al., Acta Materialia, 2017
19. Ranking for Fatigue Performance
𝜺𝜺𝑡𝑡𝑡𝑡𝑡𝑡𝑎𝑎𝑎𝑎 →
0.5% applied strain
amplitude
MKS + Explicit Integration CPFEM
Predict 𝜺𝜺𝑡𝑡𝑡𝑡𝑡𝑡𝑎𝑎𝑎𝑎
using MKS
localization
Estimate 𝜺𝜺𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝𝑝 (𝐩𝐩𝐩𝐩𝐩𝐩𝐩𝐩 − 𝐚𝐚𝐚𝐚𝐚𝐚𝐚𝐚𝐚𝐚𝐚𝐚𝐚𝐚𝐚𝐚)
Construct distribution of
extreme fatigue indicator
parameters (FIPs)
New protocol is 40X
faster than traditional
protocols for ranking
new microstructures for
fatigue resistance
𝑭𝑭𝑭𝑭𝑭𝑭 𝑭𝑭𝑭𝑭 =
∆𝜸𝜸 𝒎𝒎𝒎𝒎𝒎𝒎
𝒑𝒑
𝟐𝟐
𝟏𝟏 + 𝒌𝒌
𝝈𝝈 𝒎𝒎𝒎𝒎𝒎𝒎
𝒏𝒏
𝝈𝝈𝒚𝒚
Paulson, Priddy, McDowell, Kalidindi, Materials and Design, 154, 2018
20. Forecasting of microstructure statistics
via data-driven linkages
Phase-field simulations
Initial
Structure
Final
Structure
Autoregressive
models
Initial
microstructure
statistics (CLDs)
Final
microstructure
statistics (CLDs)
Process-Structure Evolution Linkages: Application
to solid state sintering of ceramic materials
21. 𝛼𝛼𝑡𝑡
𝑖𝑖
= 𝑓𝑓 𝛼𝛼𝑡𝑡−1
1
, … , 𝛼𝛼𝑡𝑡−𝐻𝐻
𝑅𝑅
Local Gaussian Process Autoregressive (GPAR) models
Hyperparameter
optimization
Test points for the time
step to be forecast
Selection of k-nearest
neighbors for local
prediction
Forecasting test
point with local
GPAR
Use the previously forecast
time step as input for the
prediction of next time step
Takes only around 1 min to forecast entire time evolution of PC scores of a test point!
23. High-Throughput “Autonomous” Experiments
Macroscale
• Current protocols for materials testing need significant amounts of
material produced with a consistent processing history.
• Standardized testing (e.g., tension tests) require significant effort in
making samples.
• Current protocols are not suitable for rapid screening of the
extremely large materials design space (this is the product space that
includes all chemical compositions and process histories of interest).
Microscale
• A extremely large amount of experimental data is needed to
calibrate multiscale materials constitutive models.
• Current protocols require sophisticated equipment, incur significant
time and cost, and produce only limited amount of data.
Critically need high throughput, cost-effective, protocols for
multiresolution mechanical measurements at different material
structure/length scales.
25. Applications to Rapid Screening of Process Space
0
100
200
300
400
500
600
700
200 300 400IndentationStrength[MPa]
Aging Temperature [°C]
High Throughput Sample
Individual Heat Treatments
0
100
200
300
400
500
600
700
AR 204 °C 274 °C 343 °C 413 °C
Strength[MPa]
Indentation Yield Strength
Tensile Yield Strength
29. 𝑝𝑝 𝐸𝐸 𝑪𝑪, 𝑔𝑔
Sequential Design of Experiments
Autonomous building of
a Gaussian Process
model for indentation
trained on FE model
Selection of new experiments
based on maximizing information
gain (e.g., Shannon)
30. • A physics-centered Bayesian framework can
serve as a foundational element in the design
and build of AI-based materials knowledge
systems that can provide objective decision
support in all aspects of materials innovation.
• High-throughput experimental and
computational protocols are critically needed
to generate the data needed to feed the
envisioned knowledge systems.
Summary Statements
