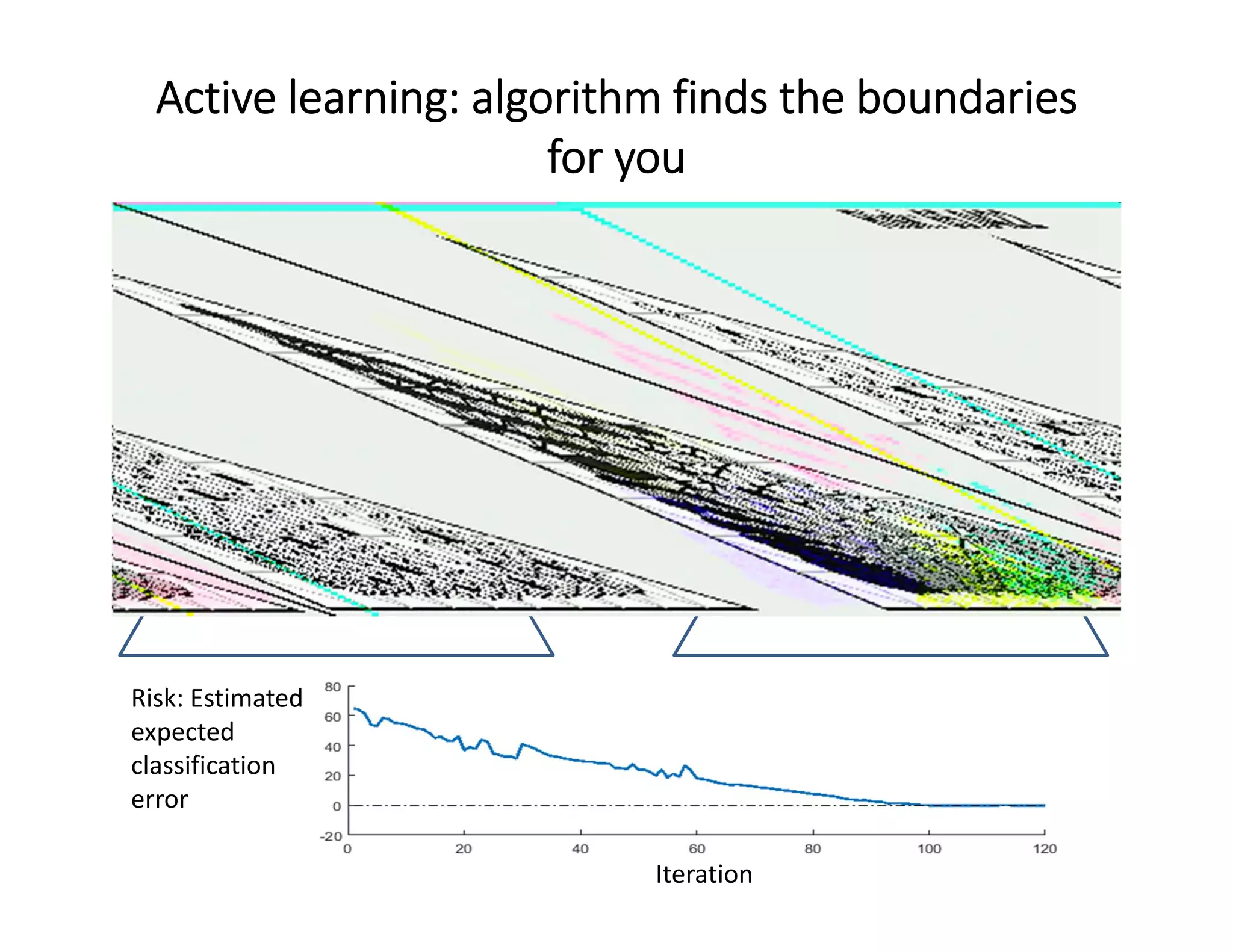
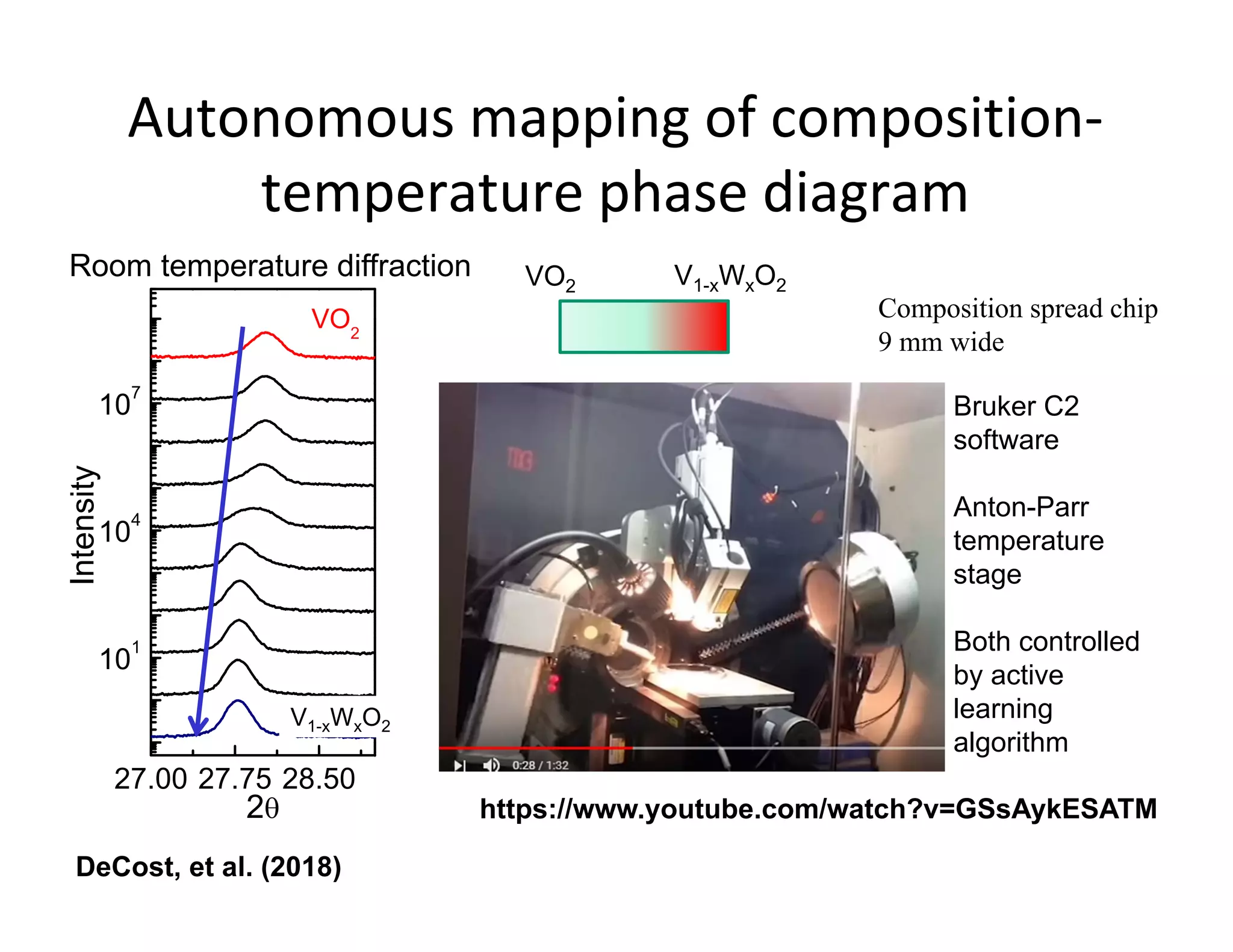
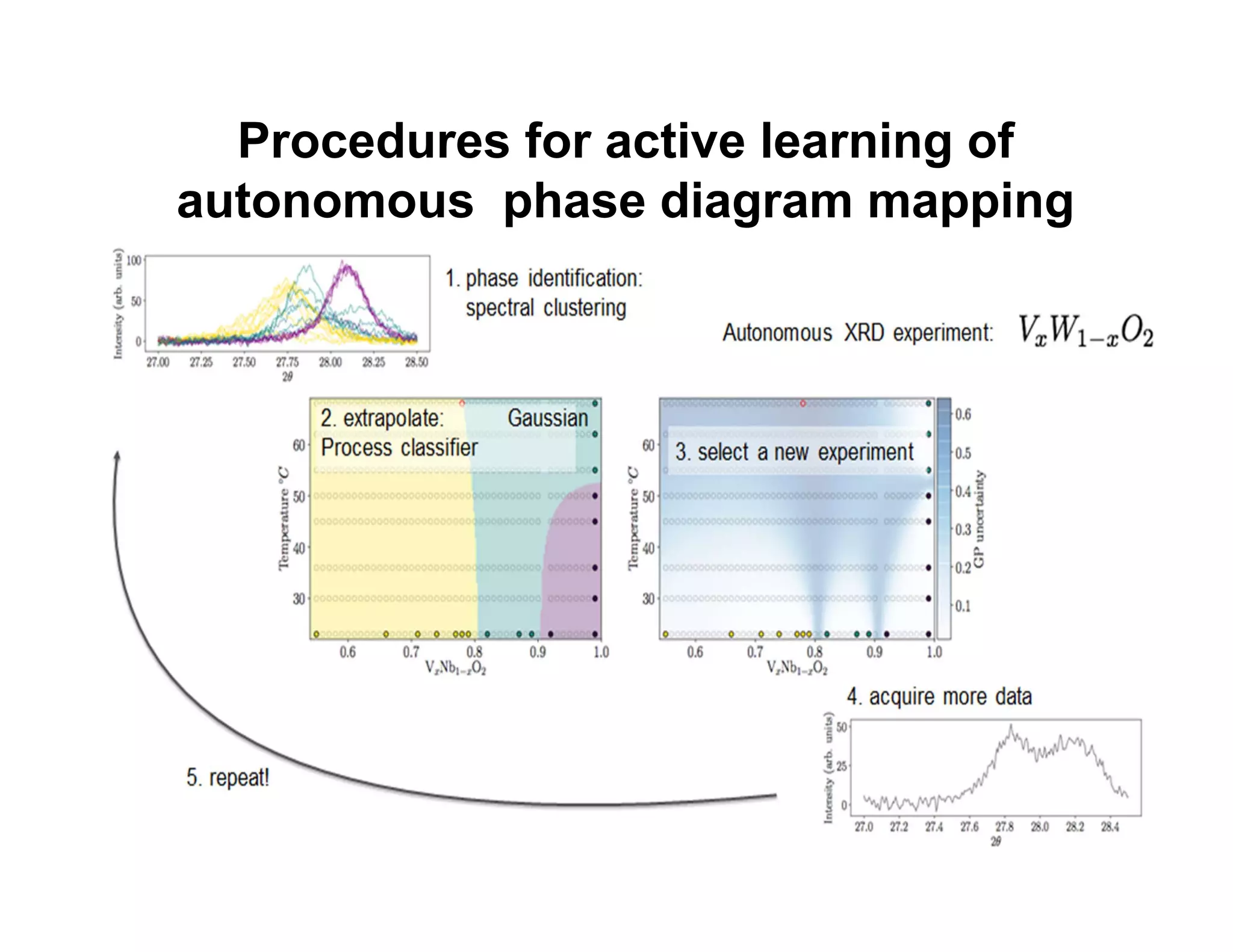
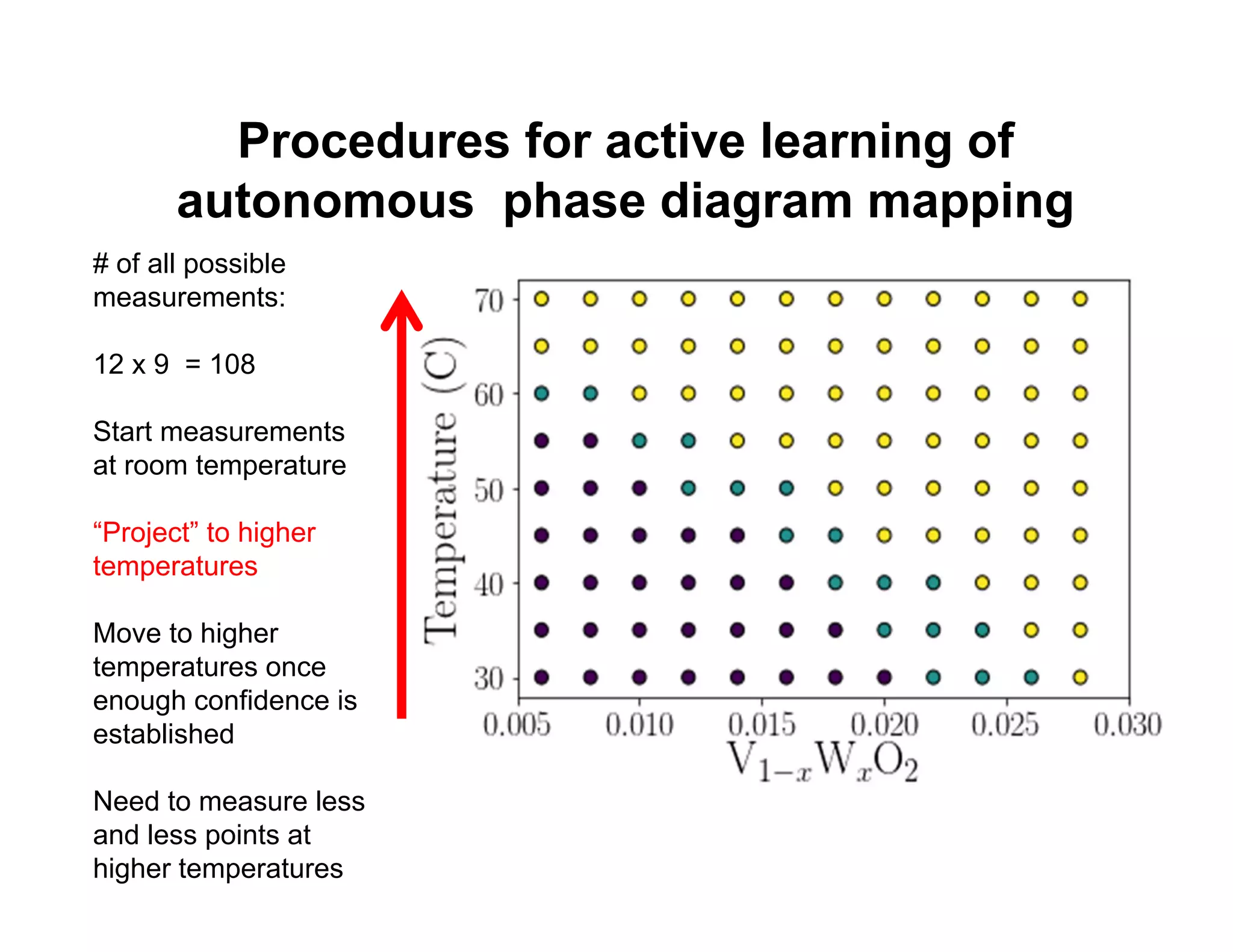
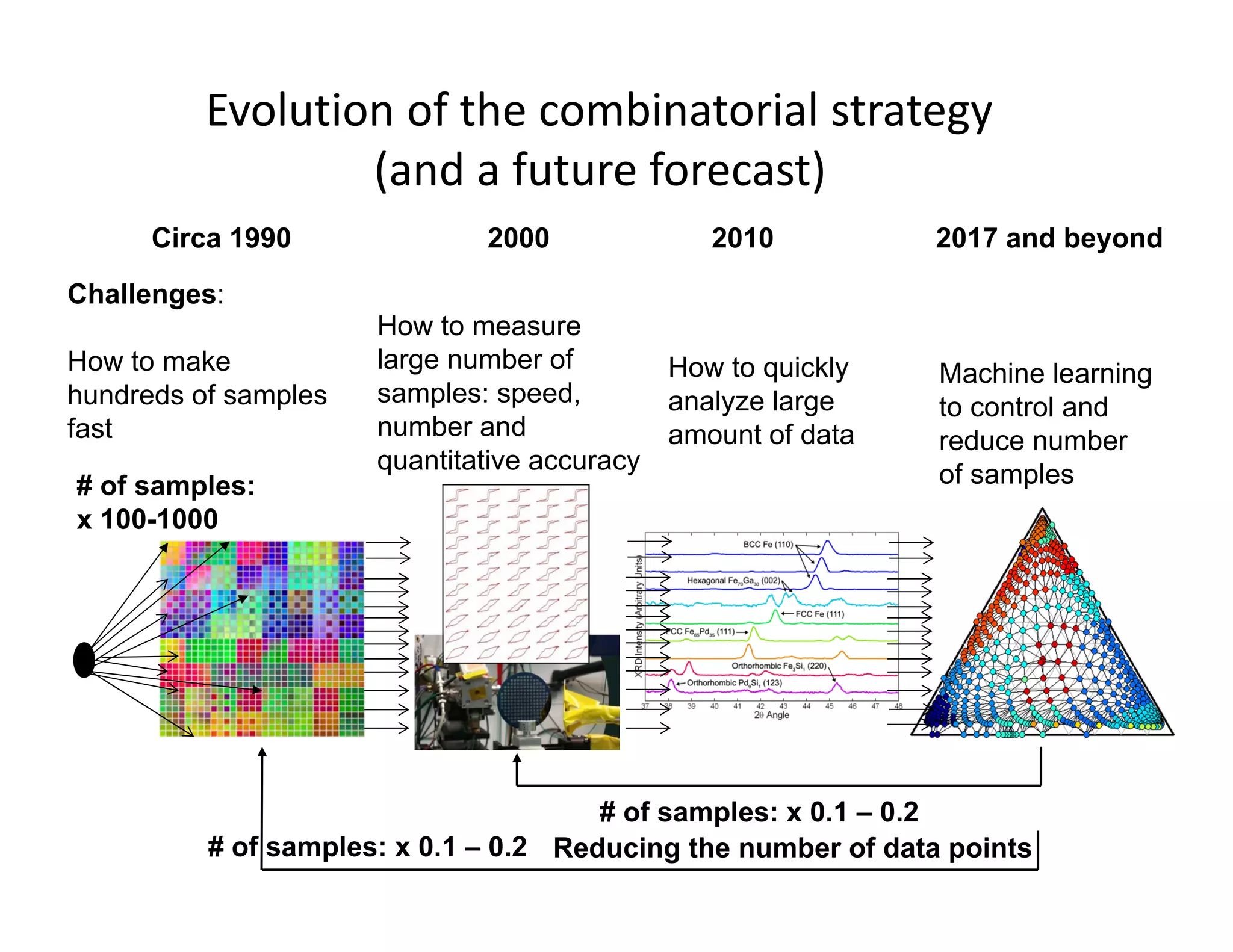
This document describes how machine learning and active learning can be used to enhance high-throughput combinatorial experimentation for materials discovery. Specifically, it discusses how active learning algorithms can direct experiments to optimally query samples and map out phase diagrams with fewer total measurements. An example is given of using these methods to autonomously map the composition-temperature phase diagram of tungsten-doped VO2 with only 10% of samples requiring direct measurement. The document concludes that machine learning has the potential to significantly reduce the number of experiments needed in combinatorial screening studies.


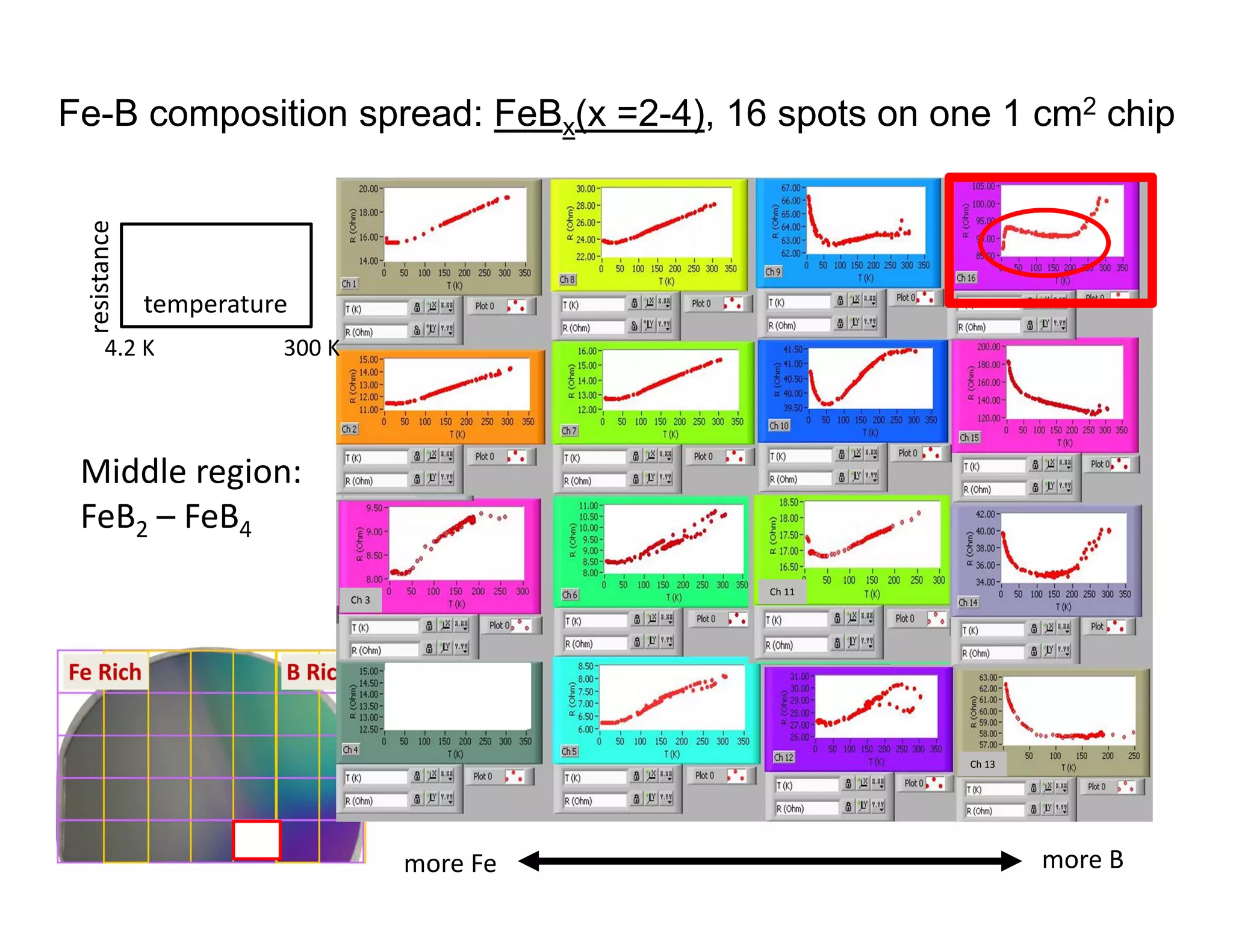
![FeBx: it looks like a real superconductor
Susceptibility
shows diamagnetism
Bc2(T)= Bc2(0)[1-(T/Tc)2]/ [1+(T/Tc)2]
gives Bc2(0) = 2 T
-> Type II BCS superconductor
Partial R drop
~ 10 K?
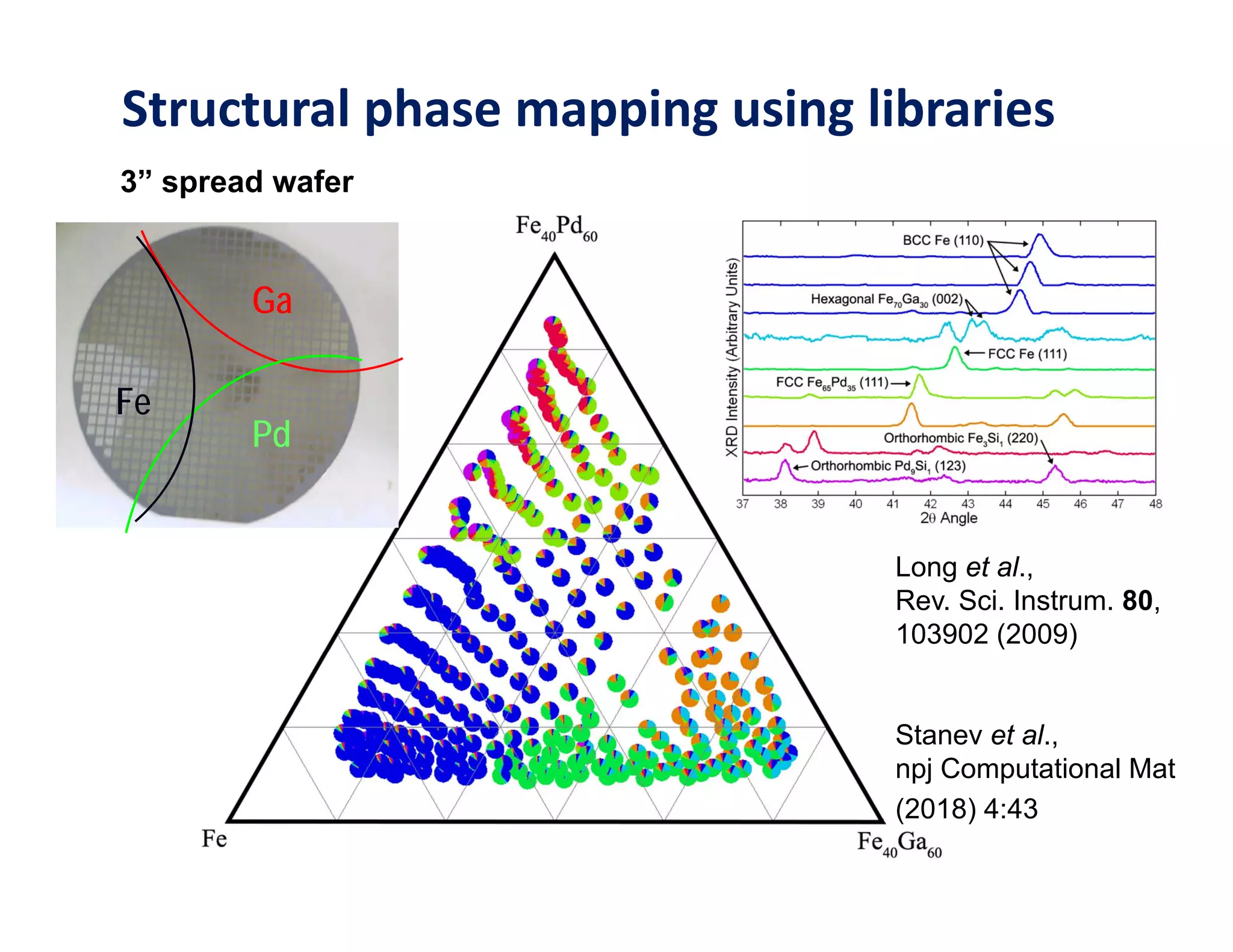
Superconducting phase was detected in 2 spread wafers
APL Materials 1, 042101 (2013)](https://image.slidesharecdn.com/ichiro-180812201024/75/Combinatorial-Experimentation-and-Machine-Learning-for-Materials-Discovery-10-2048.jpg)