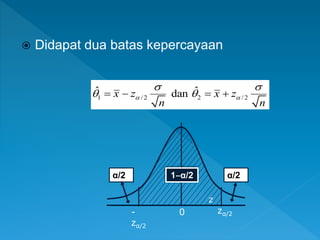
Dokumen ini membahas metode estimasi parameter populasi menggunakan sampel statistik, termasuk konsep seperti penduga, estimasi, dan interval kepercayaan. Contoh diberikan untuk menghitung selang kepercayaan rata-rata dari sampel dengan berbagai tingkat kepercayaan dan ukuran sampel. Penjelasan juga mencakup asumsi distribusi normal dan penggunaan statistik z dan t untuk penaksiran, serta contoh aplikasi dalam konteks waktu produksi dan proporsi barang rusak.

2.  Proses yang menggunakan sampel statistik
untuk menduga/ menaksir parameter
populasi yg tidak diketahui
 Penduga : suatu statistik yg digunakan
untuk menduga suatu parameter
 Estimasi: Pengukuran terhadap nilai
parameternya (populasi) dari data sampel
yang diketahui

3. 1. Tidak Bias (Unbiased) :
 apabila nilai penduga sama dengan nilai yg
diduganya
2. Efisien:
 apabila penduga memiliki varians yg kecil
3. Konsisten:
 Jika ukuran sampel semakin bertambah maka
penduga akan mendekati parameternya
 Jika ukuran sampel bertambah tak berhingga
maka distribusi sampling penduga akan mengecil
menjadi tegak lurus di atas parameter yg
sebenarnya dgn probabilitas sama dgn satu

4. Pendugaan interval
 Pendugaan yg mempunyai dua nilai sbg pembatasan/
daerah pembatasan
 Digunakan tingkat keyakinan thd daerah yg memuat
nilai sebenarnya/ nilai duga parameternya akan berada
 Nilai (1-α) disebut koefisien kepercayaan
 Nilai duga parameter dinyatakan sebagai nilai dengan
Selang kepercayaan : (1-α) x 100%

5. 1. Untuk sampel besar (n > 30)
a. Untuk populasi tdk terbatas/ populasi terbatas
yg nilai σ diketahui
n
Z
X
n
Z
X




 .
. 2
/
2
/ 



Penaksiran rata-rata sampel adalah menentukan
interval nilai rata-rata sampel yang dapat memuat
parameter rata-rata populasi, jika dipakai distribusi
probabilitas normal, confedence interval untuk rata-
rata ditentukan.

6.  Didapat dua batas kepercayaan
1 / 2 2 / 2
ˆ ˆ
dan
x z x z
n n
 
 
 
   
z
zα/2
-
zα/2
0
α/2
α/2 1‒α/2

7.  Contoh: Rata-rata IP sampel acak 36 mahasiswa
tingkat S-1 adalah 2.6. Hitung selang kepercayaan 95%
dan 99% untuk rata-rata IP semua mahasiswa S-1!
Anggap bahwa standar deviasi populasinya 0.3.
 Solusi:
Diketahui x-bar = 2.6; σ = 0.3; z0.025 = 1.96; z0.005 = 2.575
› Selang kepercayaan 95% untuk rata-rata IP semua mahasiswa
S-I:
› Interpretasi: Dapat dipercaya sebesar 95% bahwa rata-rata IP
semua mahasiswa S-1 antara 2.50 hingga 2.70
   
0.3 0.3
2.6 1.96 2.6 1.96
36 36
2.50 2.70


   
   
   
   
 

8.  Selang kepercayaan 99% untuk rata-rata IP semua mahasiswa
S-I:
 Interpretasi: Dengan tingkat kesalahan 1%, dapat dinyatakan
bahwa rata-rata IP semua mahasiswa S-1 antara 2.47 hingga
2.73.
--00--
 Perhatikan:
   
0.3 0.3
2.6 2.575 2.6 2.575
36 36
2.47 2.73


   
   
   
   
 
/ 2
x z
n


 / 2
x z
n



x 
gala
t

9. b. Untuk populasi terbatas, pengambilan
sampel tanpa pengembalian dan σ
diketahui atau n/N > 5%
1
.
.
1
.
. 2
/
2
/








N
n
N
n
Z
X
N
n
N
n
Z
X






10. 2. Untuk sampel kecil (n ≤ 30)
n
s
t
X
n
s
t
X .
. 2
/
2
/ 
  



)
1
(
)
(
1
2
2






n
n
X
n
X
s

11. Sebuah perusahaan ingin mengestimasi rata-
rata waktu yang diperlukan oleh sebuah mesin
yang digunakan untuk memproduksi satu jenis
kain. Diambil secara acak 36 pis kain, waktu
rata-rata yang diperlukan untuk memproduksi 1
pis kain adalah 15 menit. Jika diasumsikan
standar deviasi populasi 3 menit, tentukan
estimasi interval rata-rata dengan tingkat
confidence (tingkat kepercayaan) 95% ?

12. X (Rata-rata) = 15 menit
n = 36
Simpangan Baku = 3
Nilai standar Deviasi = = 3 : √36 = 0.5
Tingkat Kepercayaan 95%, dari tabel distribusi normal
diperoleh Ztabel = 1.96
14.02 < µ < 15.98
n


13. 2. Lima karyawan PT TELITI dipilih secara
acak, kemudian diukur beratnya. Datanya
adalah 62, 67, 70, 65 dan 60 kg. Buatlah
pendugaan interval rata-ratanya dgn
tingkat keyakinan 99%

14. 1. Untuk sampel besar (n > 30)
a. Untuk populasi tidak terbatas
b. Untuk populasi terbatas dan pengambilan
sampel tanpa pengembalian
n
p
p
Z
p
P
n
p
p
Z
p
)
1
(
.
)
1
(
. 2
/
2
/





 

1
)
1
(
.
1
)
1
(
. 2
/
2
/










N
n
N
n
p
p
Z
p
P
N
n
N
n
p
p
Z
p 


15. 1. Distribusi Sampling
2. Pertimbangan Lebar Interval
3. Tingkat Kepercayaan
x
x
x
z
x
z
x 

 



Tingkat
Kepercayaan
Skor Z Bentuk umum estimate
interval
90 % 1,645
95 % 1,960
99 % 2,575
x
x
x
x
x 

 645
,
1
645
,
1 



x
x
x
x
x 

 960
,
1
960
,
1 



x
x
x
x
x 

 575
,
2
575
,
2 



: error standar dari mean
x

μx : Mean populasi
Z : nilai skor z yg ditentukan dg probabilitas estimate interval

16. Sebuah peti kemas diperiksa untuk menaksir
persentase barang rusak. Untuk keperluan
tersebut, diambil 60 buah barang yang ada dalam
peti dan diperoleh 9 buah rusak. Dugalah
persentase barang yang rusak. Digunakan interval
keyakinan 99 persen

17. n = 60
X = 9
p = 9:60 = 0.15
1- α = 99%
α = 1% = 0.01
Zα/2 = Z0.005 = 2.575

18. 2. Untuk sampel kecil (n ≤ 30)
n
p
p
t
p
P
n
p
p
t
p
)
1
(
.
)
1
(
. 2
/
2
/





 

Sebuah Sampel sebanyak 25 buah apel, 8
diantaranya apel kualitas rusak. Dengan interval
keyakinan 95%, tentukan proporsi apel yang
rusak ?

19. 1. Sebuah perusahaan memproduksi baut,
menggunakan mesin otomatis dengan
diameter menyebar mengikuti distribusi
normal yang standar deviasinya (populasi)
0,02 milimeter. Diambil sampel acak empat
buah baut untuk suatu pemeriksaan,
ternyata rata-rata diameternya sebesar
24,98mm. Buatlah selang kepercayaan
dengan tingkat kepercayaan 98 persen
bagi rata-rata baut.

20. 2. Lima karyawan PT TELITI dipilih secara
acak, kemudian diukur beratnya. Datanya
adalah 62, 67, 70, 65 dan 60 kg. Buatlah
pendugaan interval rata-ratanya dgn tingkat
keyakinan 99%
3. Dari sampel random 400 orang yg makan
siang di restoran NIKMAT selama beberapa
hari Sabtu, diperoleh data 125 org yg
menyukai makanan tradisional. Tentukan
pendugaan interval bagi proporsi sebenarnya,
orang yg menyukai makanan tradisional utk
makan siangnya pd hari Sabtu di restoran
tersebut dgn menggunakan interval
keyakinan 98%