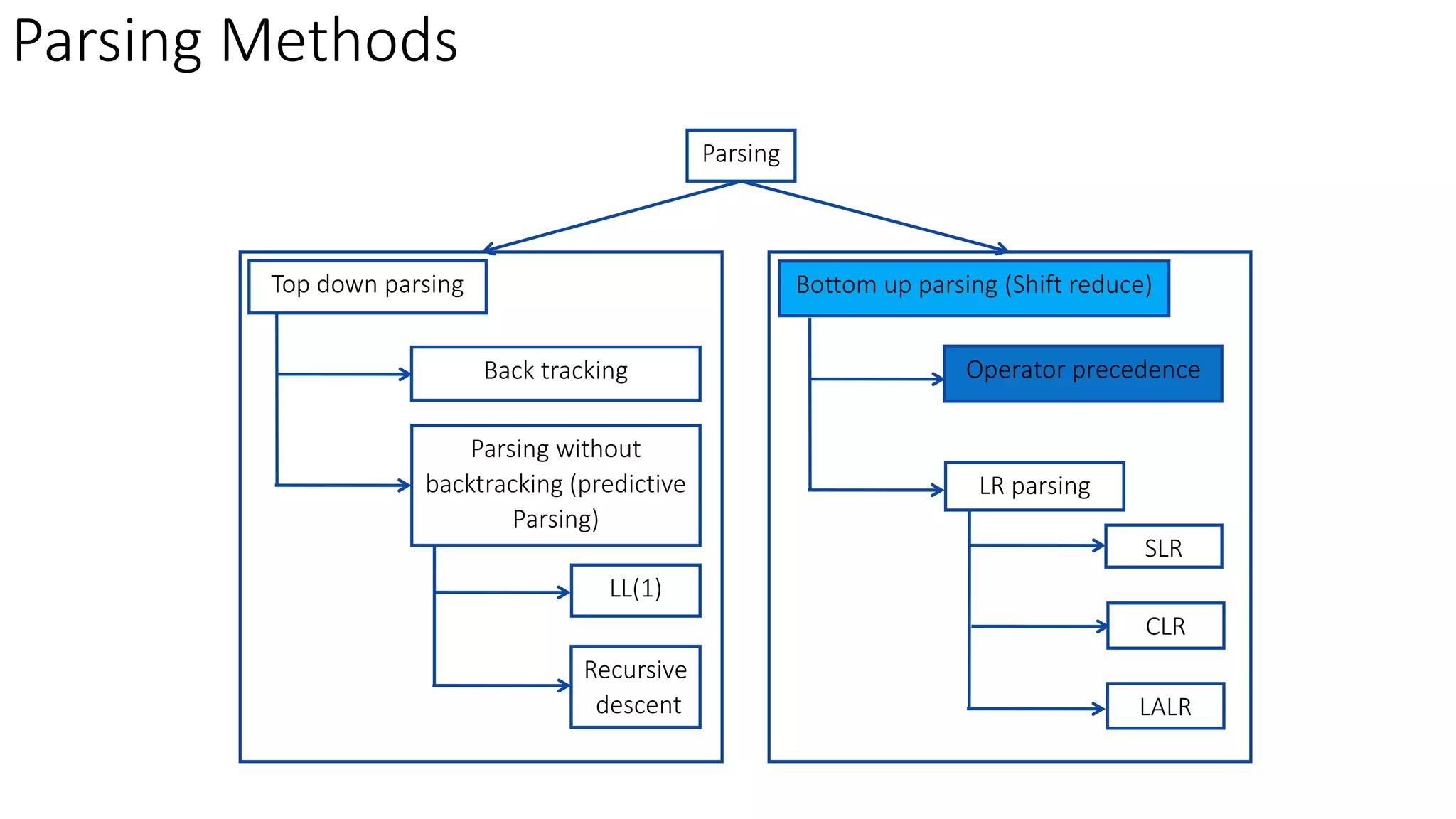
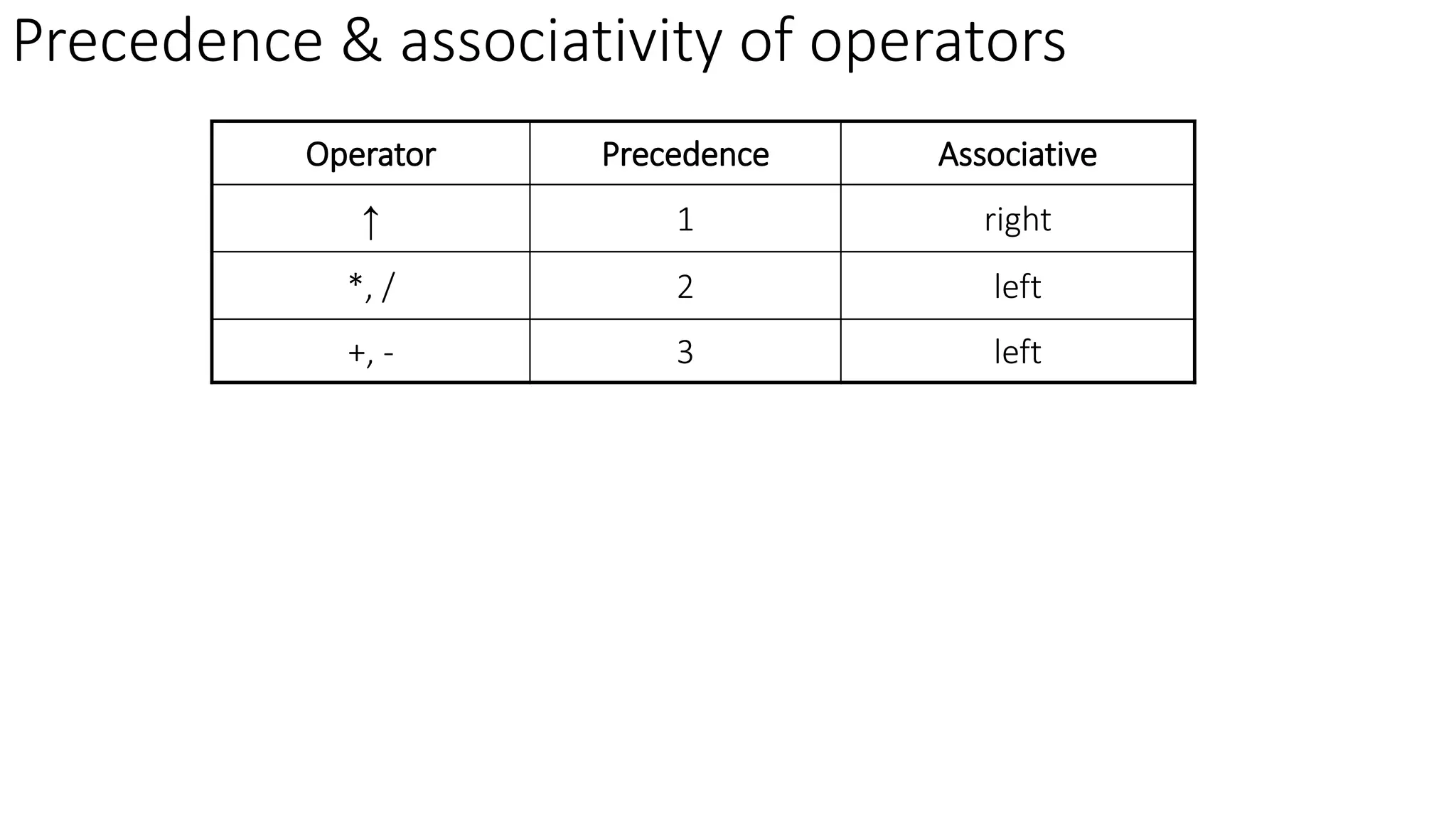
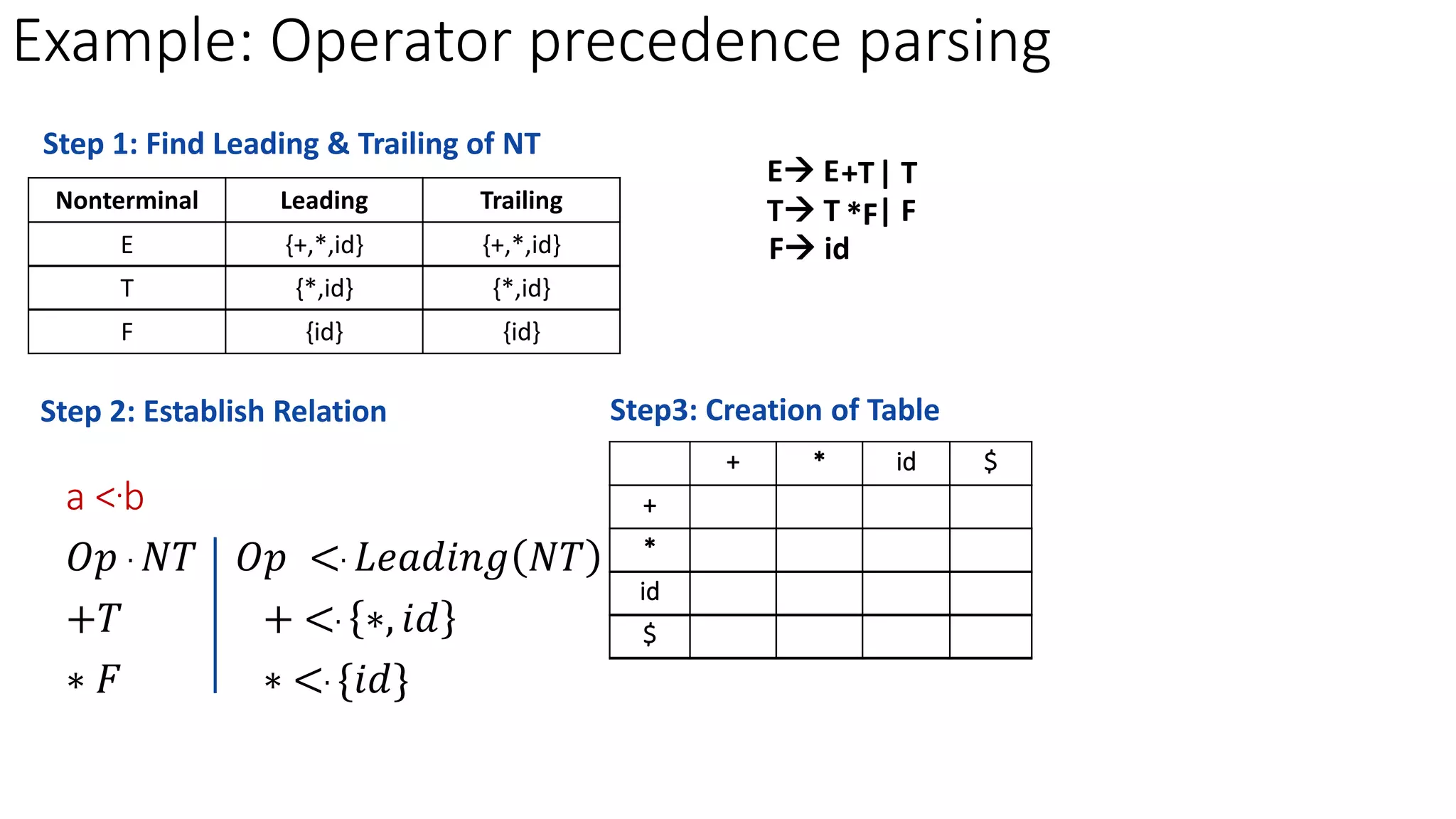
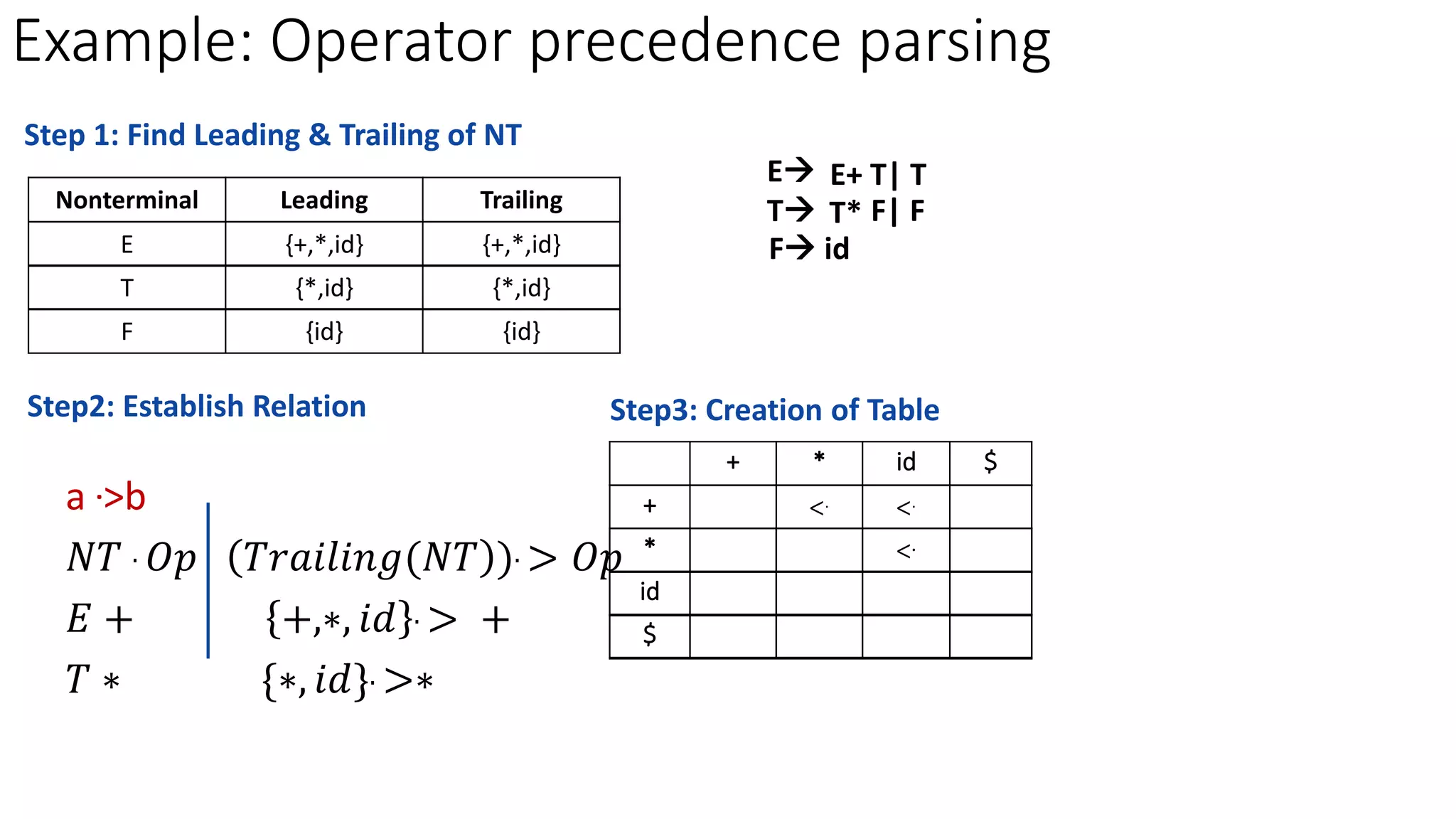
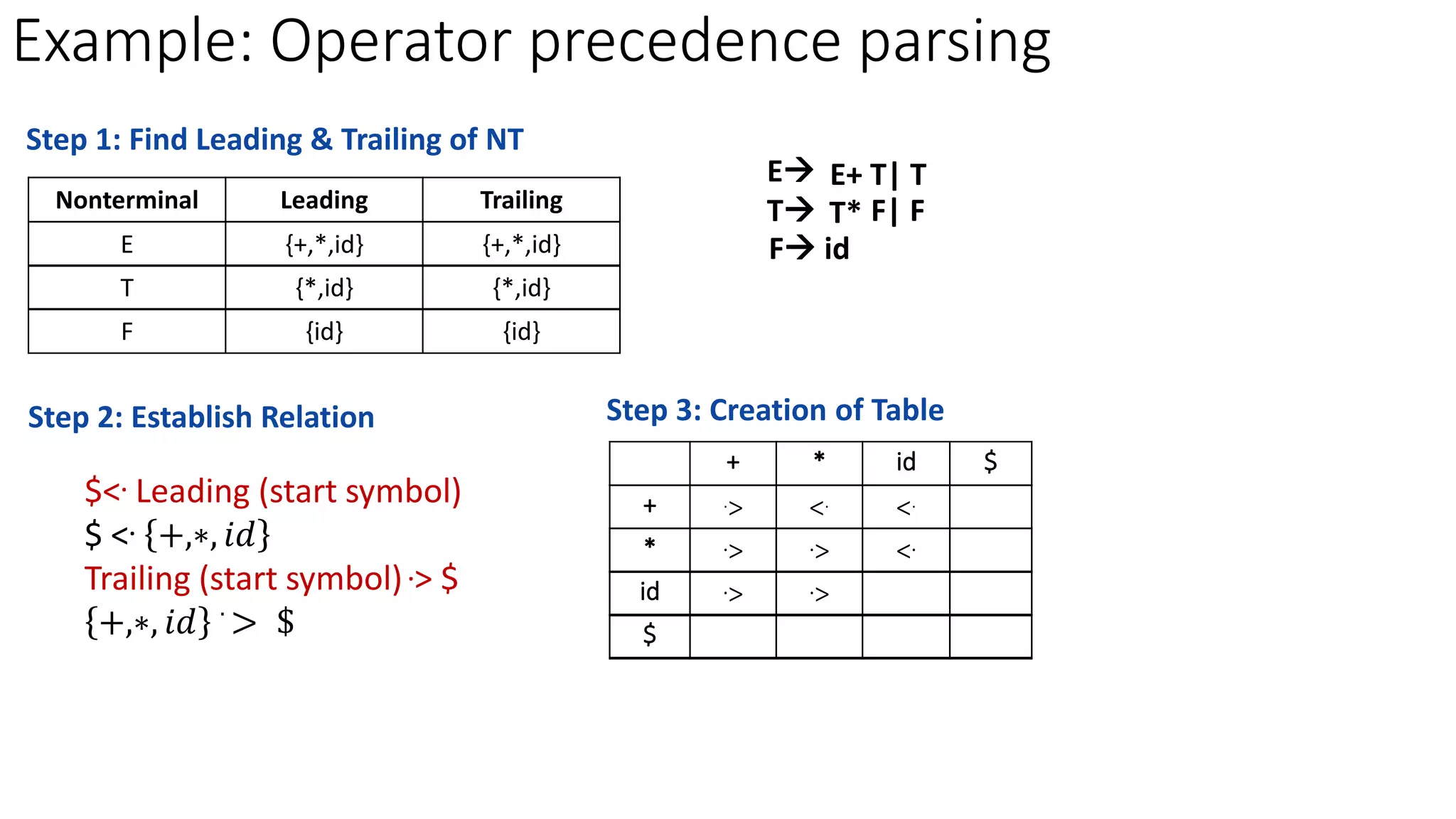
1. Operator precedence parsing involves defining precedence relations between operators based on their associativity and precedence. It uses these relations to parse strings based on which operator has higher precedence at each step. 2. The key steps are to find the leading and trailing non-terminals, establish precedence relations between terminals, create a precedence table, and then parse strings using the table. 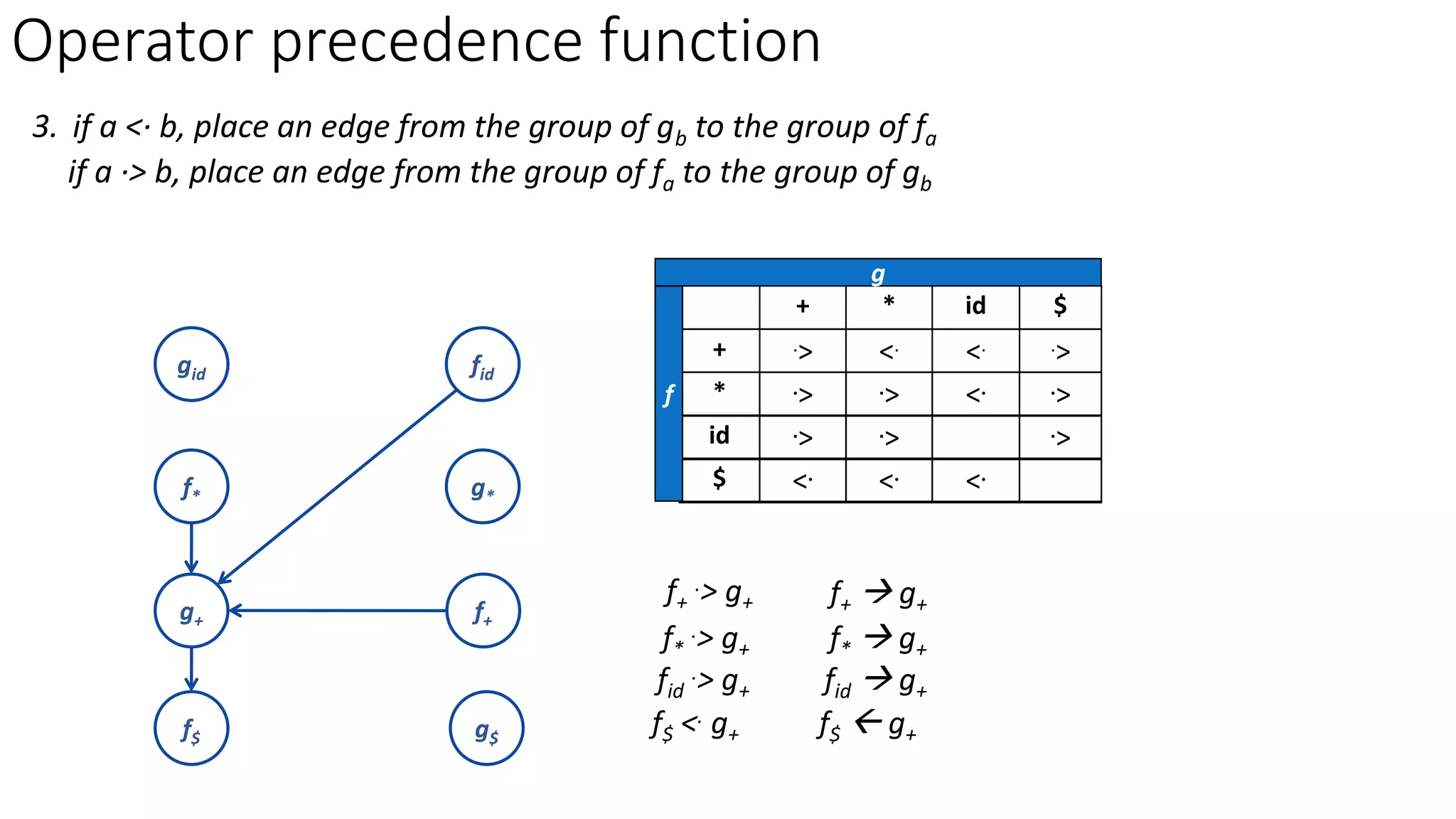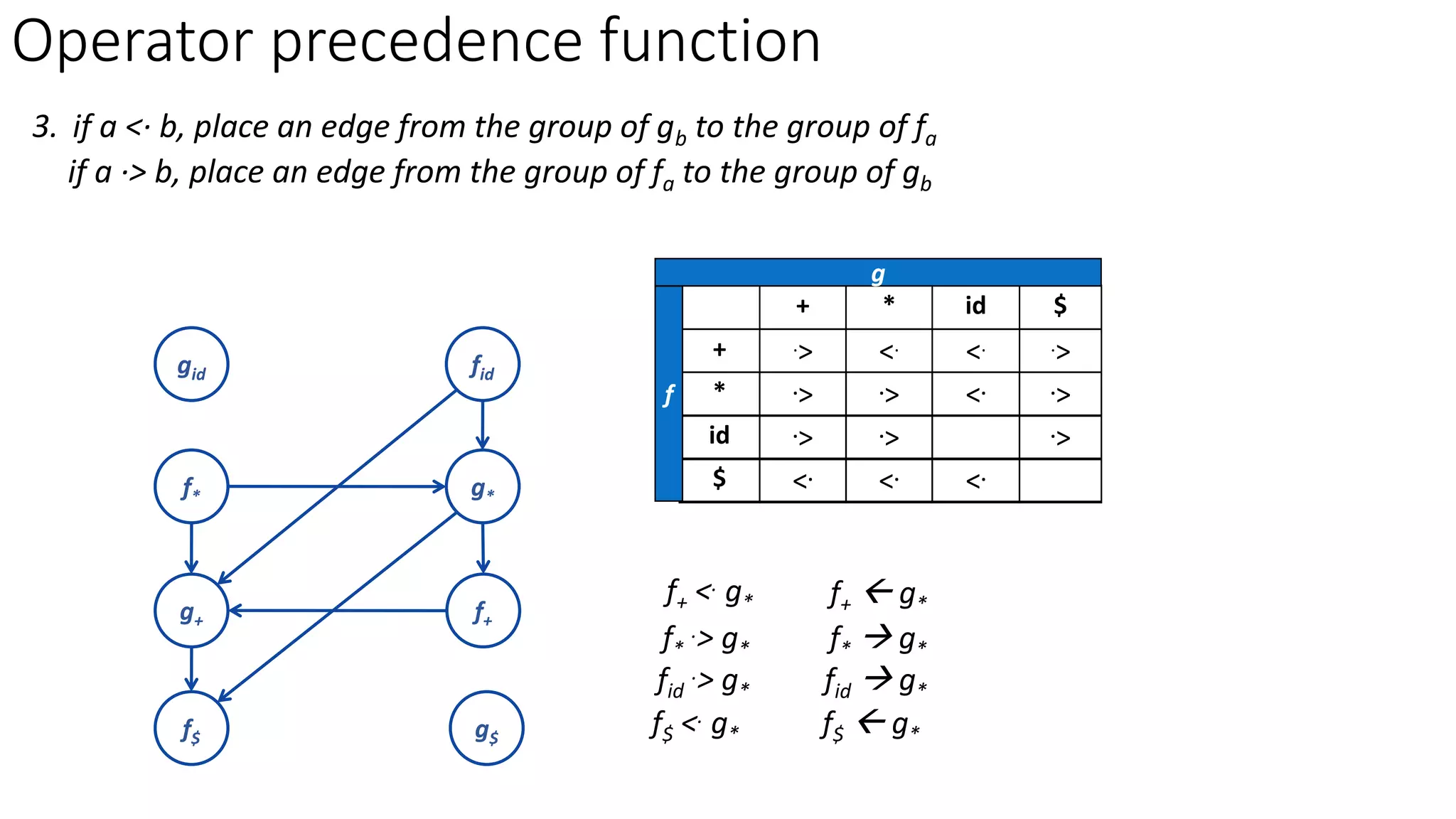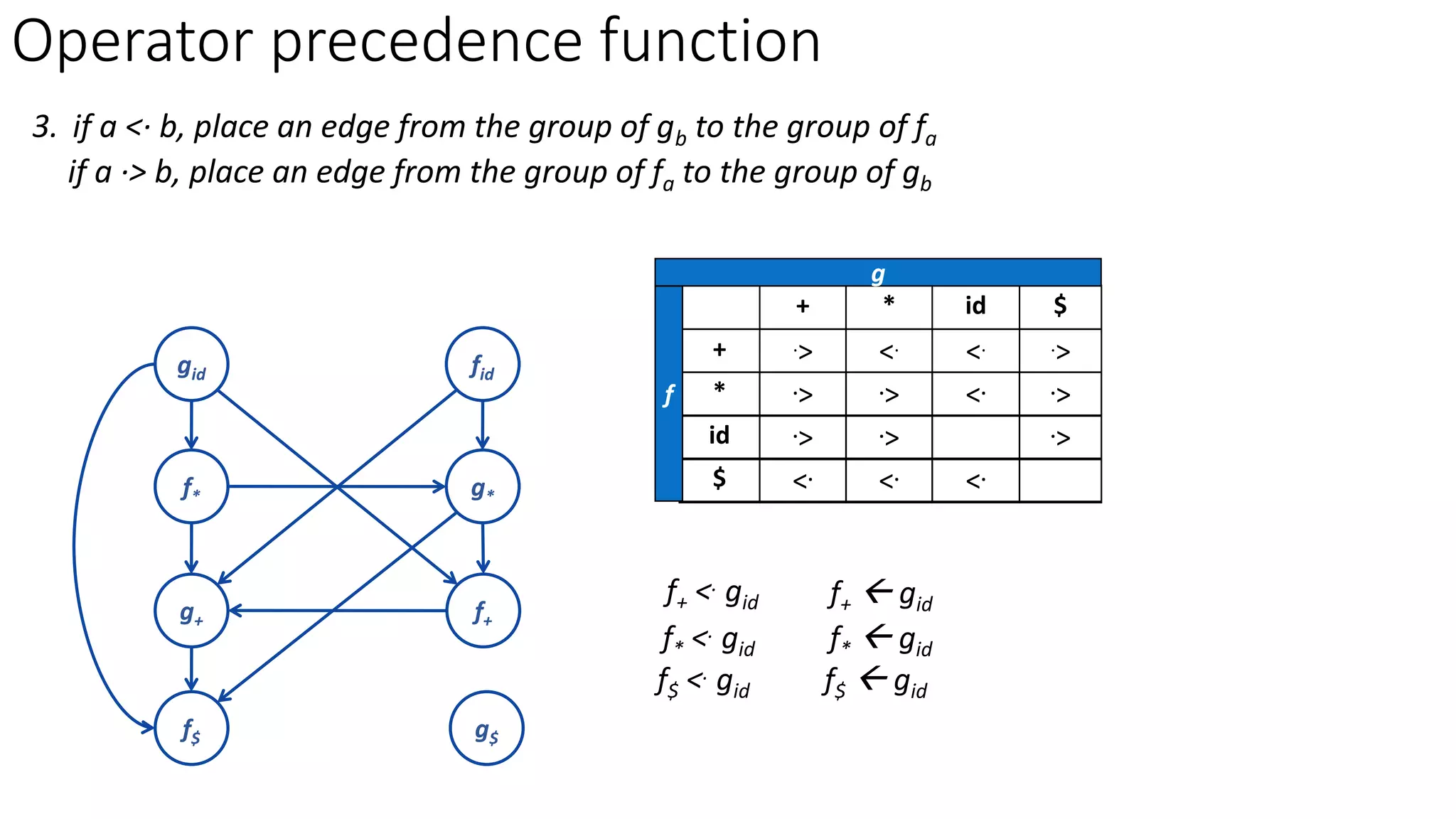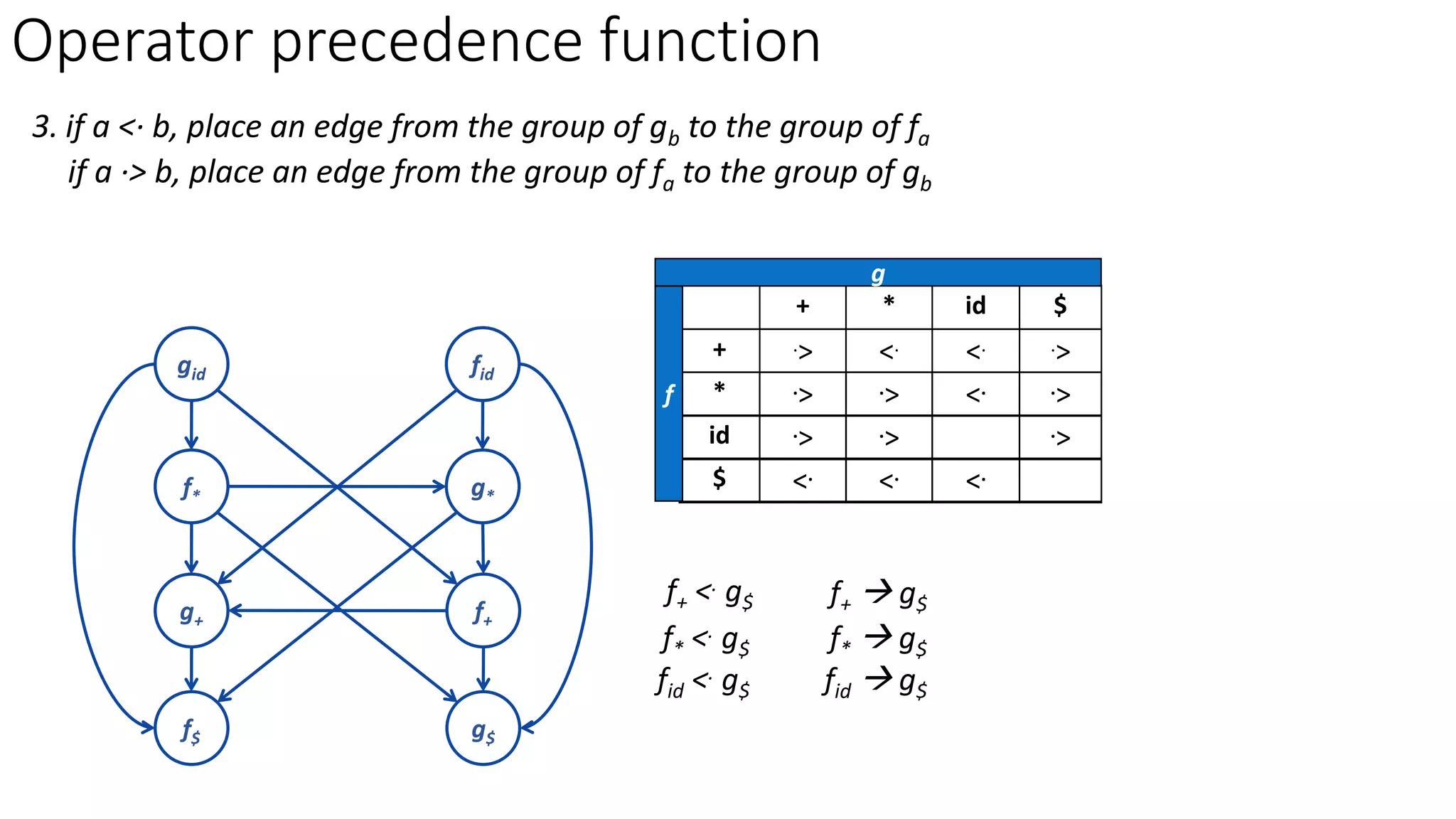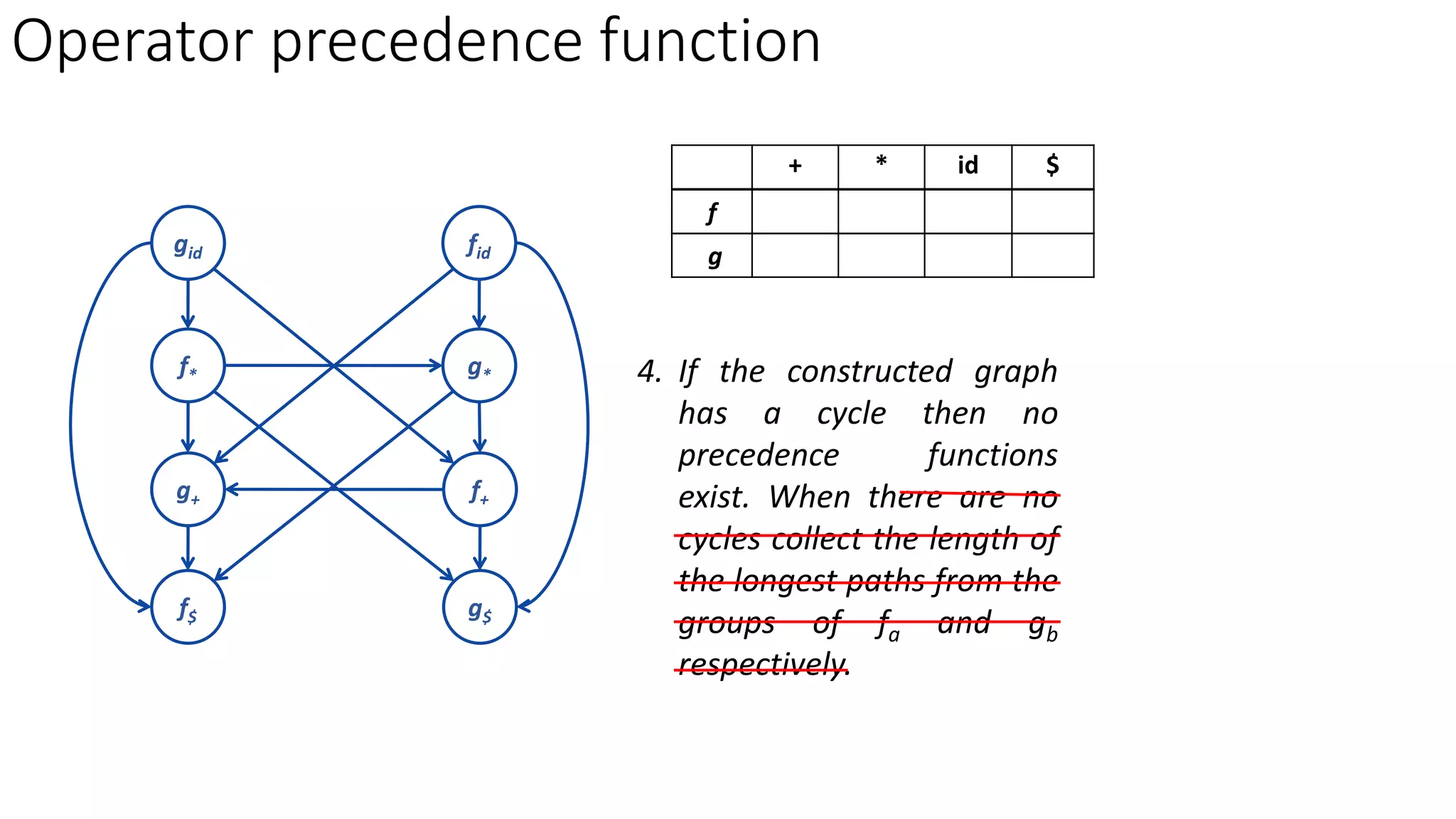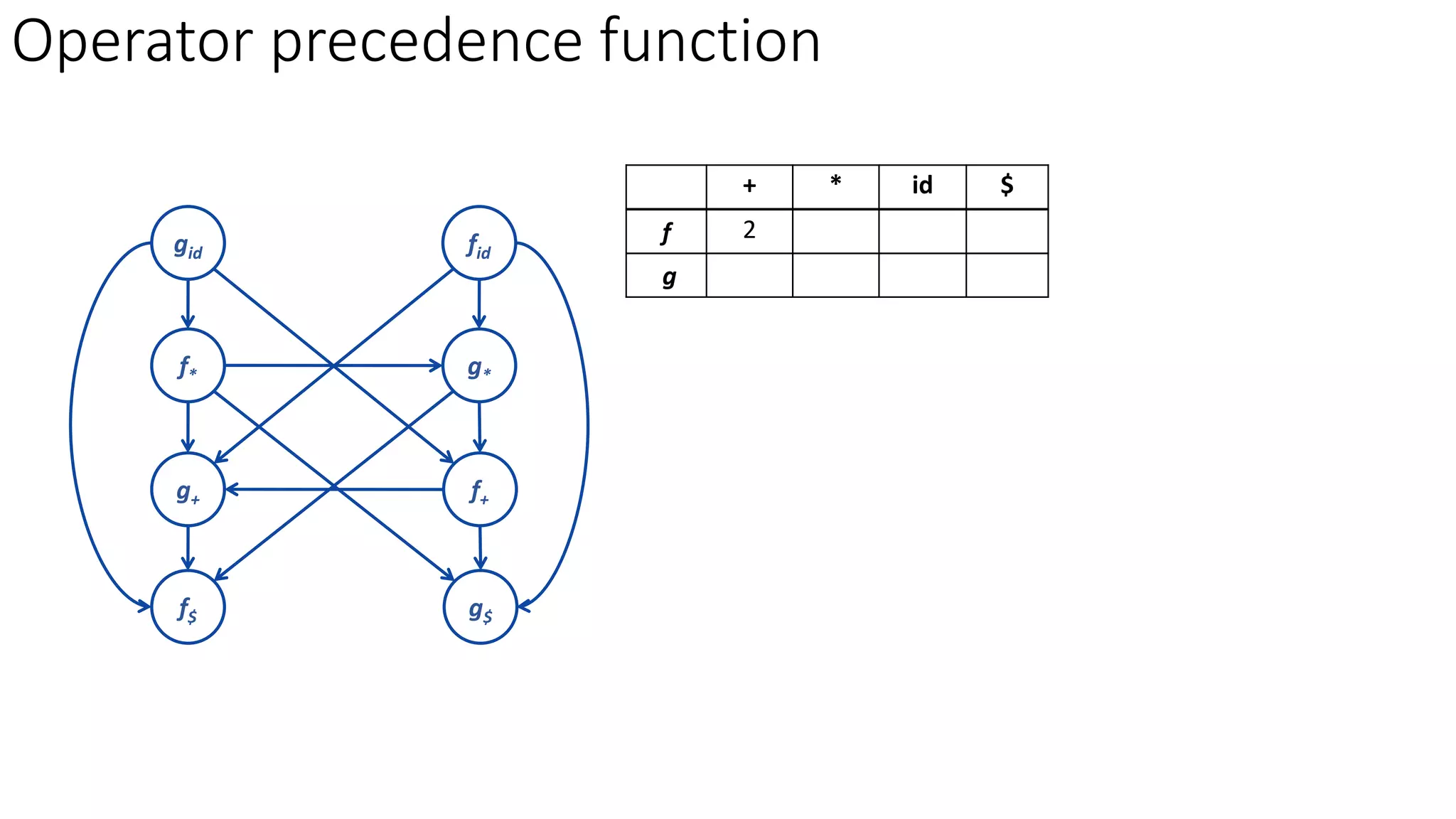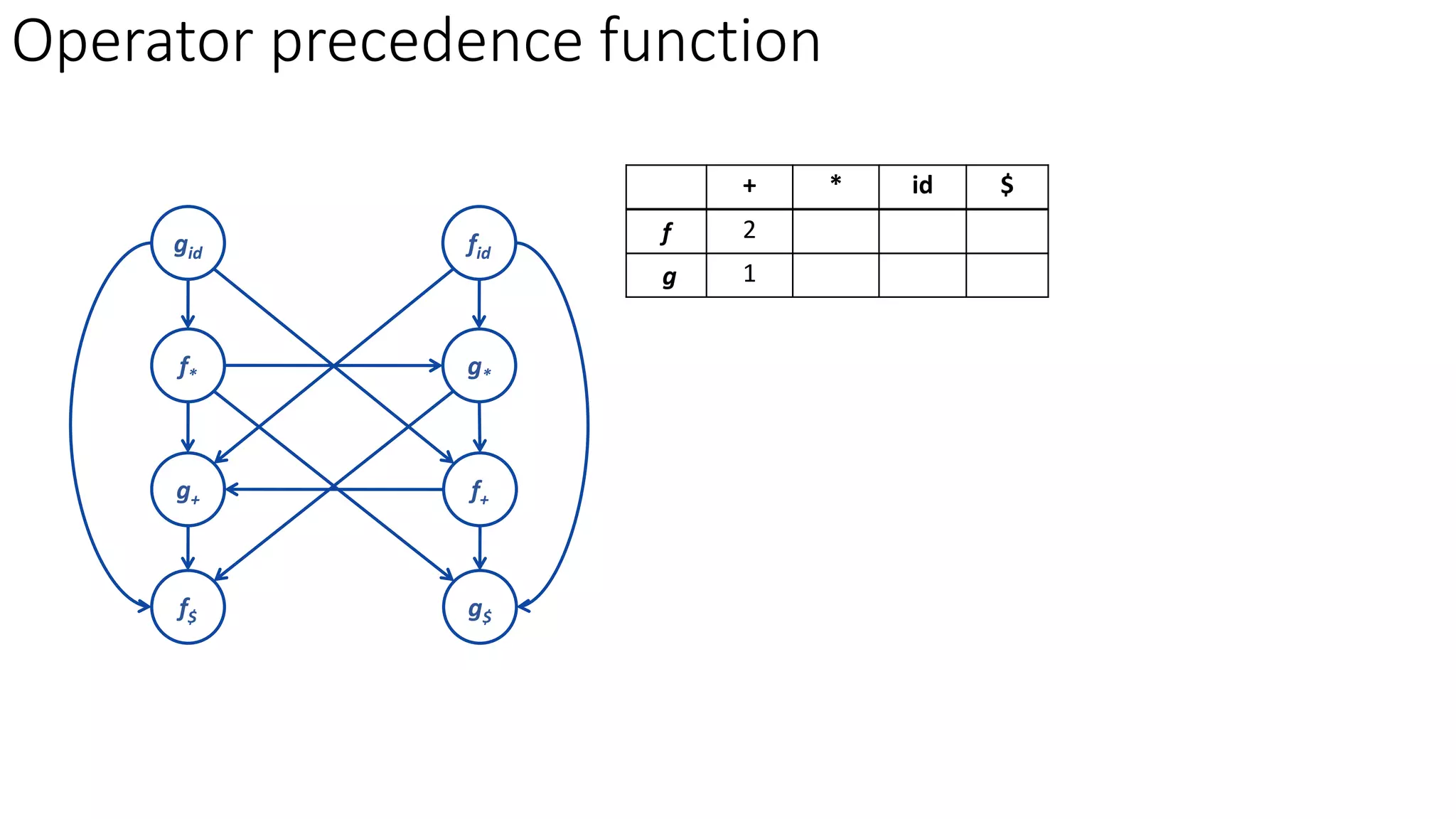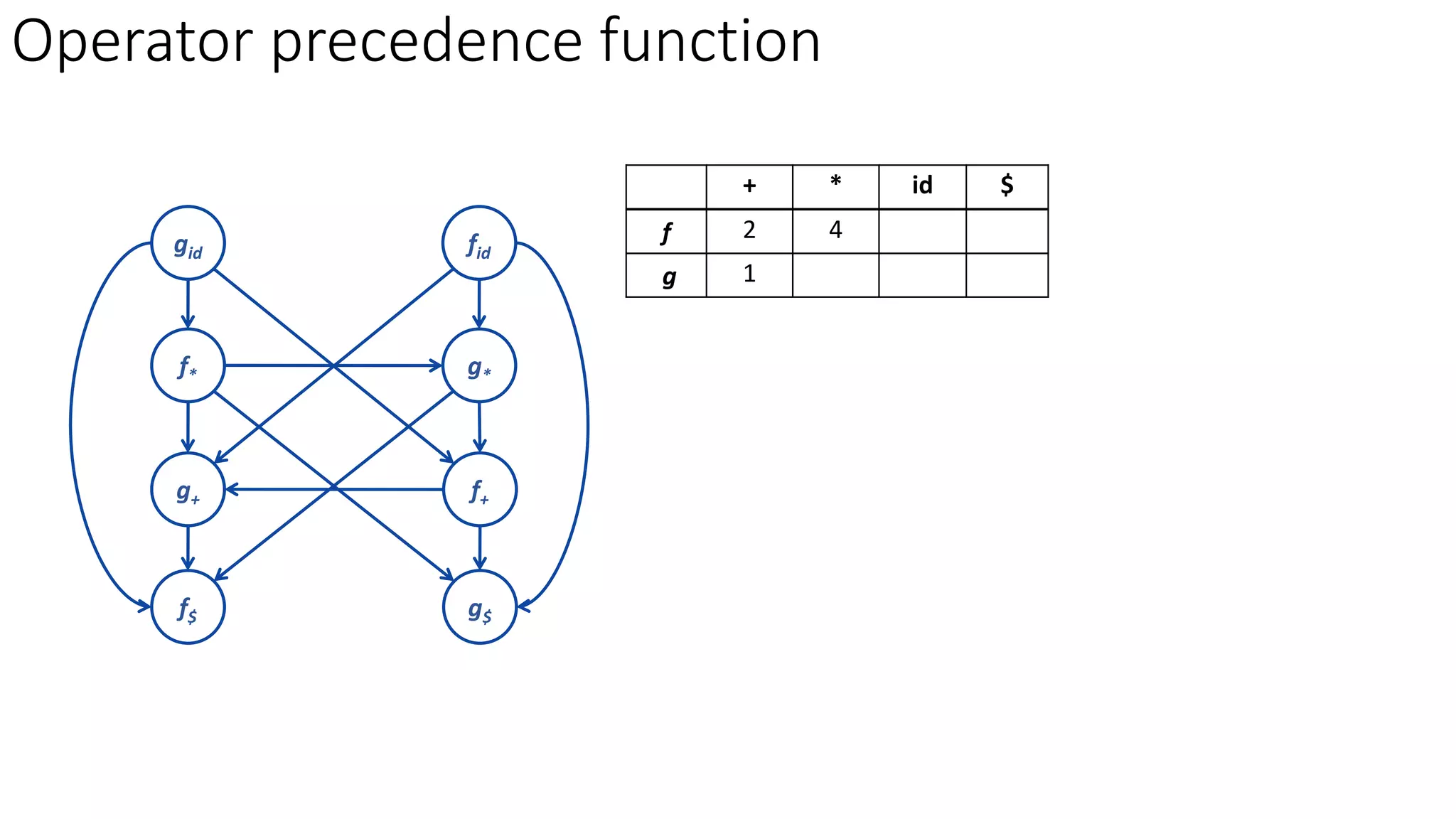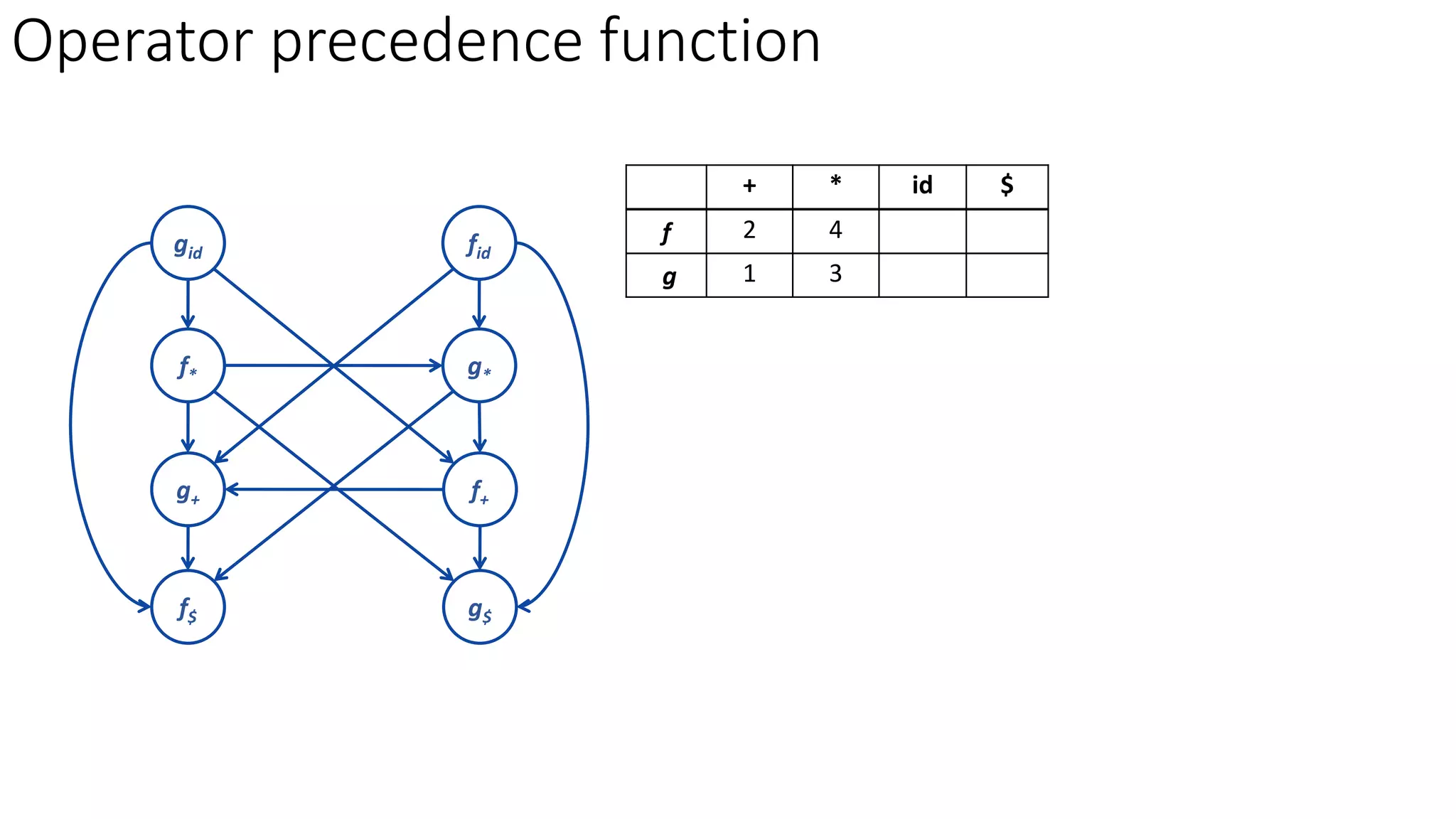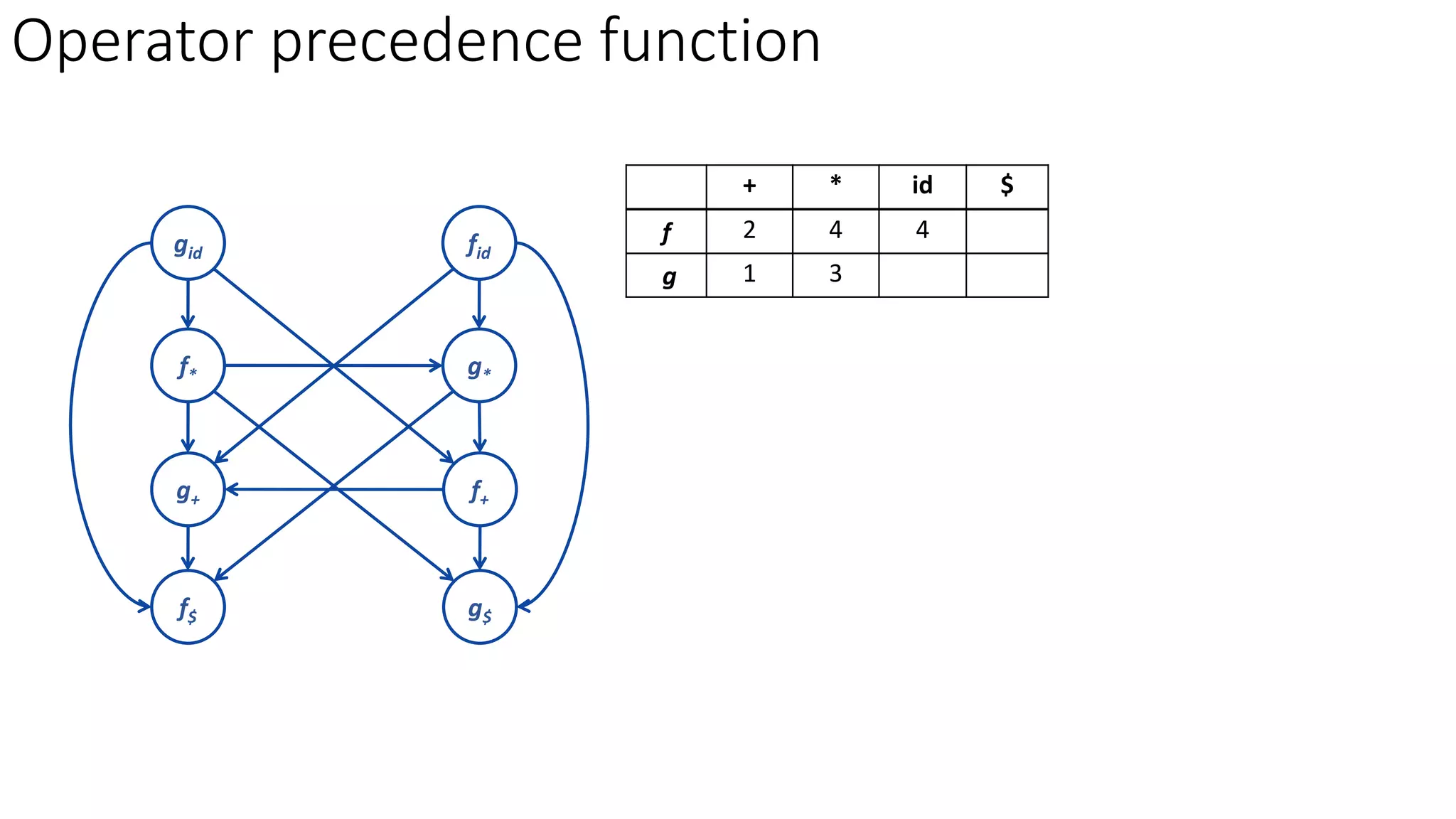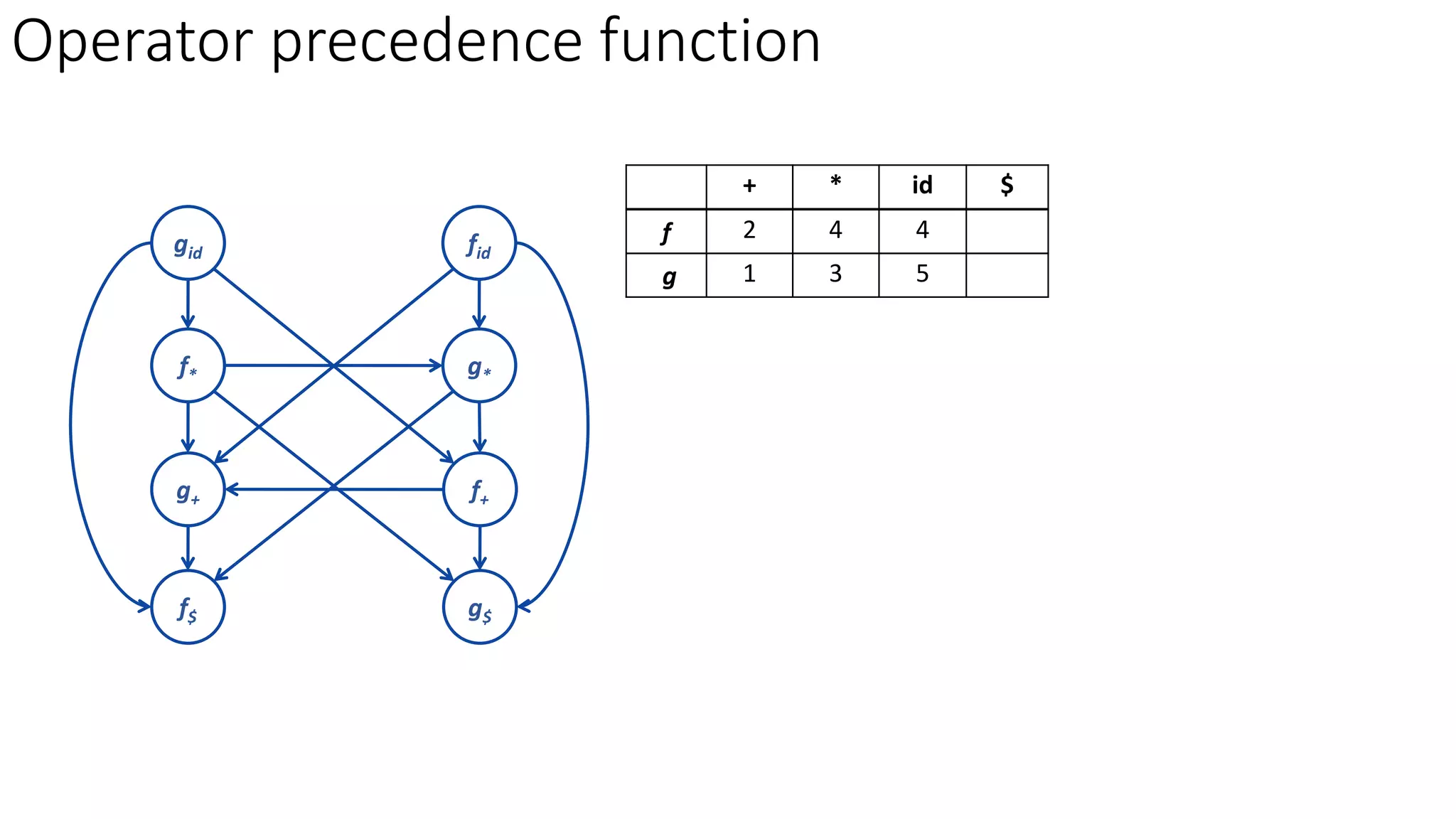3. Operator precedence functions can also be constructed by partitioning symbols into groups based on equality, creating a directed graph from the precedence relations, and finding the longest paths between each symbol's function groups. The path lengths give the precedence functions.

1. Parsing Methods
Parsing
Top down parsing Bottom up parsing (Shift reduce)
Back tracking
Parsing without
backtracking (predictive
Parsing)
LR parsing
Operator precedence
LALR
CLR
SLR
Recursive
descent
LL(1)

2. Operator precedence parsing
• Operator Grammar: A Grammar in which there is no Є in RHS of any production
or no adjacent non terminals is called operator grammar.
• Example: E EAE | (E) | id
A + | * | -
• Above grammar is not operator grammar because right side EAE has
consecutive non terminals.
• In operator precedence parsing we define following disjoint relations:
Relation Meaning
a<.b a “yields precedence to” b
a=b a “has the same precedence as” b
a.>b a “takes precedence over” b

3. Precedence & associativity of operators
Operator Precedence Associative
↑ 1 right
*, / 2 left
+, - 3 left

4. Steps of operator precedence parsing
1. Find Leading and trailing of non terminal
2. Establish relation
3. Creation of table
4. Parse the string

5. Leading & Trailing
Leading:- Leading of a non terminal is the first terminal or operator in production
of that non terminal.
Trailing:- Trailing of a non terminal is the last terminal or operator in production
of that non terminal.
Example: EE+T | T
TT*F | F
Fid
Non terminal Leading Trailing
E {+,*,id} {+,*,id}
T {*,id} {*,id}
F {id} {id}

6. Rules to establish a relation
1. For a = b, ⇒ 𝑎𝐴𝑏, where 𝐴 is 𝜖 or a single non terminal [e.g : (E)]
2. a <.b ⇒ 𝑂𝑝 . 𝑁𝑇 𝑡ℎ𝑒𝑛 𝑂𝑝 <. 𝐿𝑒𝑎𝑑𝑖𝑛𝑔 𝑁𝑇 [e.g : +T]
3. a .>b ⇒ 𝑁𝑇 . 𝑂𝑝 𝑡ℎ𝑒𝑛 𝑇𝑟𝑎𝑖𝑙𝑖𝑛𝑔(𝑁𝑇 ) . > 𝑂𝑝 [e.g : E+]
4. $ <. Leading (start symbol)
5. Trailing (start symbol) .> $

7. Example: Operator precedence parsing
1. a <.b
2. 𝑂𝑝 . 𝑁𝑇 𝑂𝑝 <. 𝐿𝑒𝑎𝑑𝑖𝑛𝑔 𝑁𝑇
3. +𝑇 + <. ∗, 𝑖𝑑
4. ∗ 𝐹 ∗ <. {𝑖𝑑}
Nonterminal Leading Trailing
E {+,*,id} {+,*,id}
T {*,id} {*,id}
F {id} {id}
Step 1: Find Leading & Trailing of NT
Step 2: Establish Relation
E E
Step3: Creation of Table
+ * id $
+ .> <. <. .>
* .> .> <. .>
id .> .> .>
$ <. <. <.
+T| T
T T *F| F
F id

8. Example: Operator precedence parsing
1. a .>b
2. 𝑁𝑇 . 𝑂𝑝 𝑇𝑟𝑎𝑖𝑙𝑖𝑛𝑔(𝑁𝑇 ). > 𝑂𝑝
3. 𝐸 + +,∗, 𝑖𝑑 . > +
4. 𝑇 ∗ {∗, 𝑖𝑑}. >∗
Nonterminal Leading Trailing
E {+,*,id} {+,*,id}
T {*,id} {*,id}
F {id} {id}
Step2: Establish Relation
E
Step3: Creation of Table
+ * id $
+ .> <. <. .>
* .> .> <. .>
id .> .> .>
$ <. <. <.
E+ T| T
T T* F| F
F id
Step 1: Find Leading & Trailing of NT

9. Example: Operator precedence parsing
Nonterminal Leading Trailing
E {+,*,id} {+,*,id}
T {*,id} {*,id}
F {id} {id}
Step 2: Establish Relation
E
Step 3: Creation of Table
+ * id $
+ .> <. <. .>
* .> .> <. .>
id .> .> .>
$ <. <. <.
E+ T| T
T T* F| F
F id
Step 1: Find Leading & Trailing of NT
1. $<. Leading (start symbol)
2. $ <. +,∗, 𝑖𝑑
3. Trailing (start symbol).> $
4. +,∗, 𝑖𝑑
.
> $

10. Example: Operator precedence parsing
Assign precedence operator between terminals
String: id+id*id
$ id+id*id $
$ <. id+id*id$
$ <. id .> +id*id$
$ <. id .> + <. id*id$
$ <. id .> + <. id .> *id$
$ <. id .> + <. id .> *<. id$
$ <. id .> + <. id .> *<. id .> $
+ * id $
+ .> <. <. .>
* .> .> <. .>
id .> .> .>
$ <. <. <.
Step 4: Parse the string using precedence table

11. Example: Operator precedence parsing
$ <. Id .> + <. Id .> * <. Id .> $ Handle id is obtained between <. and .>
Reduce this by Fid
$ F + <. Id .> * <. Id .> $ Handle id is obtained between <. and .>
Reduce this by Fid
$ F + F * <. Id .> $ Handle id is obtained between <. and .>
Reduce this by Fid
$ F + F * F $ Perform appropriate reductions of all nonterminals.
$ E + T * F $ Remove all non terminals.
$ + * $ Place relation between operators
$ <. + <. * >$ The * operator is surrounded by <. and .>. This
indicates * becomes handle so reduce by TT*F.
$ <. + >$ + becomes handle. Hence reduce by EE+T.
$ $ Parsing Done
Step 4: Parse the string using precedence table
1. Scan the input string until first .> is encountered.
2. Scan backward until <. is encountered.
3. The handle is string between <. and .>

12. Operator precedence function
Algorithm for constructing precedence functions
1. Create functions 𝑓𝑎 and 𝑔𝑎 for each a that is terminal or $.
2. Partition the symbols in as many as groups possible, in such a way that 𝑓𝑎 and 𝑔𝑏 are in the
same group if 𝑎 = 𝑏.
3. Create a directed graph whose nodes are in the groups, next for each symbols 𝑎 𝑎𝑛𝑑 𝑏 do:
a) if 𝑎 <· 𝑏, place an edge from the group of 𝑔𝑏 to the group of 𝑓𝑎
b) if 𝑎 ·> 𝑏, place an edge from the group of 𝑓𝑎 to the group of 𝑔𝑏
4. If the constructed graph has a cycle then no precedence functions exist. When there are no
cycles collect the length of the longest paths from the groups of 𝑓𝑎 and 𝑔𝑏 respectively.

13. Operator precedence function
1. Create functions fa and ga for each a that is terminal or $.
𝑎 = {+,∗, 𝑖𝑑} 𝑜𝑟 $
E E+T | T
T T*F | F
F id
f+
f* fid f$
g+
g* gid g$

14. Operator precedence function
• Partition the symbols in as many as groups possible, in such a way that fa and gb
are in the same group if a = b.
f+
f*
fid
f$
g+
g*
gid
g$
+ * id $
+ .> <. <. .>
* .> .> <. .>
id .> .> .>
$ <. <. <.
.

15. Operator precedence function
3. if a <· b, place an edge from the group of gb to the group of fa
if a ·> b, place an edge from the group of fa to the group of gb
f+
f*
fid
f$
g+
g*
gid
g$
f+
.> g+ f+  g+
f*
.> g+ f*  g+
fid
.> g+ fid  g+
f$ <. g+ f$  g+
+ * id $
+ .> <. <. .>
* .> .> <. .>
id .> .> .>
$ <. <. <.
f
g

16. Operator precedence function
3. if a <· b, place an edge from the group of gb to the group of fa
if a ·> b, place an edge from the group of fa to the group of gb
f+
f*
fid
f$
g+
g*
gid
g$
f+ <. g* f+  g*
f*
.> g* f*  g*
fid
.> g* fid  g*
f$ <. g* f$  g*
+ * id $
+ .> <. <. .>
* .> .> <. .>
id .> .> .>
$ <. <. <.
f
g

17. Operator precedence function
3. if a <· b, place an edge from the group of gb to the group of fa
if a ·> b, place an edge from the group of fa to the group of gb
f+
f*
fid
f$
g+
g*
gid
g$
f+ <. gid f+  gid
f* <. gid f*  gid
f$ <. gid f$  gid
+ * id $
+ .> <. <. .>
* .> .> <. .>
id .> .> .>
$ <. <. <.
f
g

18. Operator precedence function
3. if a <· b, place an edge from the group of gb to the group of fa
if a ·> b, place an edge from the group of fa to the group of gb
f+
f*
fid
g+
g*
gid
+ * id $
+ .> <. <. .>
* .> .> <. .>
id .> .> .>
$ <. <. <.
f+ <. g$ f+  g$
f* <. g$ f*  g$
fid <. g$ fid  g$
f
g
f$ g$

19. Operator precedence function
+ * id $
f 2
g
f+
f*
fid
f$
g+
g*
gid
g$
4. If the constructed graph
has a cycle then no
precedence functions
exist. When there are no
cycles collect the length of
the longest paths from the
groups of fa and gb
respectively.

20. Operator precedence function
+ * id $
f 2
g 1
f+
f*
fid
f$
g+
g*
gid
g$

21. Operator precedence function
+ * id $
f 2 4
g 1
f+
f*
fid
f$
g+
g*
gid
g$

22. Operator precedence function
+ * id $
f 2 4
g 1 3
f+
f*
fid
f$
g+
g*
gid
g$

23. Operator precedence function
+ * id $
f 2 4 4
g 1 3
f+
f*
fid
f$
g+
g*
gid
g$

24. Operator precedence function
+ * id $
f 2 4 4
g 1 3 5
f+
f*
fid
f$
g+
g*
gid
g$

25. Operator precedence function
+ * id $
f 2 4 4 0
g 1 3 5 0
f+
f*
fid
f$
g+
g*
gid
g$