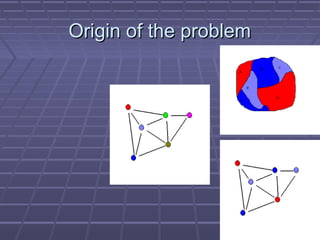
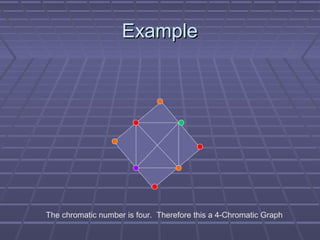
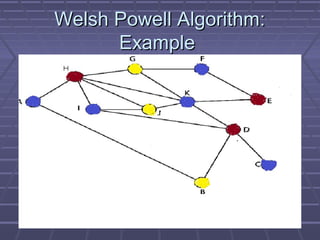
This document summarizes a presentation on graph coloring. Graph coloring involves assigning colors to the vertices of a graph such that no two adjacent vertices have the same color. It has applications in problems like channel assignment. The document defines key terms like k-coloring, chromatic number, and k-chromatic graphs. It also discusses the NP-complete nature of the graph coloring problem and summarizes basic greedy and Welsh-Powell algorithms for graph coloring.